六年级数学圆柱与圆锥练习题ppt课件
- 格式:ppt
- 大小:21.00 KB
- 文档页数:10




苏教版六年级数学下册第二单元《圆柱和圆锥》一课一练第一课时《圆柱和圆锥的认识》一、下面的图形中,哪些是圆柱,哪些是圆锥?是圆柱的在括号里打“√”,是圆锥的在括号里打“×”。
二、把第一行的图形沿虚线旋转一周后会得到哪一个图形?连-连。
三、填空1.圆柱的上、下两个面叫作(),它们是完全相同的两个()。
围成圆柱的曲面叫做()。
2.圆柱的两个底面之间的距离叫作圆柱的(),圆柱有()条高。
3.从圆锥的顶点到()的距离叫作圆锥的高。
圆锥有()条高。
4.当圆柱的底面周长和高相等时,把它的侧面展开后会得到()形。
5.将一个圆柱沿着它底面直径平均切成两半,所得截面是一个( )形或()。
将一个圆锥沿着它的高平均切成两半,截面是一个( )形。
6.用一张长20厘米,宽15厘米的长方形纸,可以卷()种纸筒。
当它们的底面周长是20厘米时,高是()厘米。
四、判断1.圆柱的侧面展开后不一定是长方形。
( )2.一个物体上、下两个面是相等的圆面,那么它一定是圆柱形物体。
( )3.把两张形状、大小完全一样的长方形纸分别卷成两个形状不同的圆筒(接头处不重叠),并装上两个底面,制成圆柱。
那么这两个圆柱的底面积、高一定相等。
()五、解决问题1.小圆给妈妈买了一盒生日蛋糕(如图),捆扎这个蛋糕盒所用的彩带至少有多长?(打结处大约用25厘米)第二课时《圆柱的侧面积》一、填空1.圆柱的侧面展开后得到的是长方形,长是圆柱的(),宽是圆柱的( )。
2.一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )。
3.一个圆柱的底面半径是5cm,高是10cm,它的侧面积是( )cm²4.一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是()平方厘米。
5.把一根直径是20 厘米,长是2 米的圆柱形木材据成同样的3段,表面积增加了( )平方厘米。
6.一个圆柱体的侧面积是125.6平方厘米,底面半径是2分米,它的高是( )厘米.7.一个圆柱,它的高增加1厘米,它的侧面积就增加50.24平方厘米,这个圆柱的底面半径是( )厘米。

1 圆柱和圆柱的侧面积1.一个长20厘米,宽4厘米的长方形面积为( )。
2.找找生活中哪些物体的形状是圆柱。
3.阅读教材第28页例题。
议一议:怎样计算罐头盒的侧面积?分析与解答:罐头盒是一个( ),沿着它的一条高将它的侧面剪开,可得到一个( ),因此,计算这个罐头盒的侧面积,即计算这个( )的面积。
其中,( )等于罐头盒的底面周长,( )等于罐头盒的高,所以,罐头盒的侧面积=( )。
4.(1)圆柱有( )个相同的底面,底面是( ),圆柱的上、下两个面之间的距离叫圆柱的( )。
(2)圆柱的侧面是一个( )面。
侧面展开是一个( )形。
这个( )形的长等于圆柱的( ),宽等于圆柱的( )。
5.圆柱的侧面积=( )×( )6.判断。
(对的画“ ”,错的画“✕”)(1)圆柱的侧面展开后一定是长方形。
( )(2)如果一个物体上、下两个面是面积相等的两个圆,那么它的形状一定是圆柱。
( )(3)圆柱的高有无数条。
( )7.把一个圆柱的侧面展开得到一个正方形,这个圆柱的底面半径是3分米,圆柱的侧面积是多少平方分米?(得数保留整数)知识准备:圆的面积、长方形的面积。
学具准备:罐头盒。
巩固练习1.下面哪些物体是圆柱?在下面的括号里画“√”。
2.填空题。
(1)把一个棱长6厘米的正方体削成一个最大的圆柱,圆柱的底面直径是( )厘米,高是( )厘米。
(2)一个圆柱的底面直径是3厘米,高也是3厘米,侧面展开的长方形的长是( )厘米,宽是( )厘米。
(3)一个圆柱的底面周长是16分米,高是8分米,侧面积是( )平方分米。
(4)一个圆柱的底面直径是10厘米,高是8厘米,侧面积是( )平方厘米。
(5)一个圆柱的底面半径是0.3米,高是0.5米,侧面积是( )平方米。
3.判断题。
(对的画“√”,错的画“✕”)(1)圆柱的高只有一条。
( )(2)圆柱两个底面的直径相等。
( )(3)圆柱的底面周长和高相等时,展开后的侧面一定是个正方形。





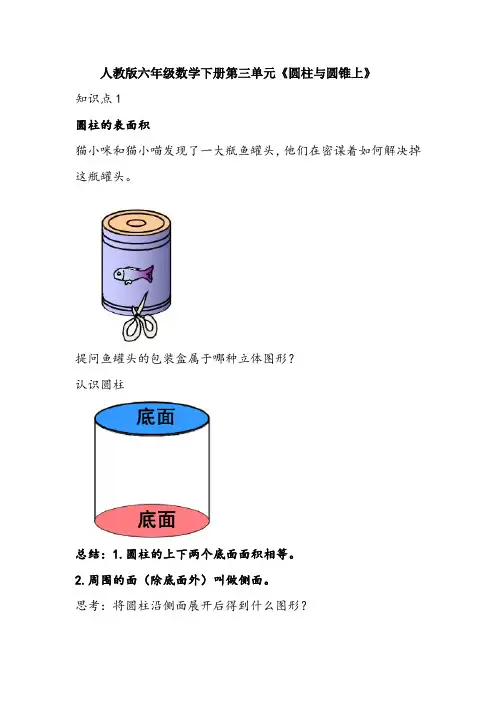
人教版六年级数学下册第三单元《圆柱与圆锥上》知识点1圆柱的表面积猫小咪和猫小喵发现了一大瓶鱼罐头,他们在密谋着如何解决掉这瓶罐头。
提问鱼罐头的包装盒属于哪种立体图形?认识圆柱总结:1.圆柱的上下两个底面面积相等。
2.周围的面(除底面外)叫做侧面。
思考:将圆柱沿侧面展开后得到什么图形?思考1.圆柱的侧面积=底面周长×高。
S侧=2πrh。
2.圆柱的表面积=圆柱的侧面积+两个底面圆的面积。
S表=2πrh+2πr²思考:一个圆柱体底面半径是1厘米,高是5厘米,那么它的侧面积和表面积分别是多少?(π取3.14)步骤:圆柱的表面积分为几个部分?三部分:两个底面积和一个侧面积。
两个底面积是多少?S底=3.14×1²×2=6.28平方厘米。
侧面积是多少?侧面积=底面周长×高。
S侧=3.14×1×2×5=31.4平方厘米。
圆柱体的表面积是多少?6.28+31.4=37.68平方厘米。
思考:如果把圆柱横着切一刀,它的表面积有什么变化?总结:切一刀表面积增加两个圆的面积。
思考:把一根长1米的圆柱分成3段,表面积增加了48平方厘米,原来圆柱的表面积是多少平方厘米?(π取3)步骤:分成三段增加几个面?(3-1)×2=4个。
圆柱的底面半径是多少厘米?48÷4=12平方厘米。
12÷3=4 4=2×2。
所以半径是2厘米。
原来圆柱的表面积是多少?1米=100厘米2×3×2×100=1200平方厘米1200+12×2=1224平方厘米思考:把一张长方形铁皮按图剪开,正好能制成一个圆柱形水桶(有盖),那么这个水桶的表面积是多少平方厘米?(π取3.14,接头处忽略不计)步骤:水桶的表面积包含哪几部分?两个底面圆的面积和侧面积。
圆柱的底面周长等于右侧小长方形的长还是宽?等于小长方形的长。
圆柱与圆锥立体图形表面积体积h r圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱h r圆锥22ππ360nS l r =+=+圆锥侧面积底面积 注:l 是母线,即从顶点到底面圆上的线段长21π3V r h =圆锥体【基础练习】一、选一选。
(将正确答案的序号填在括号里) 1、下面物体中,( )的形状是圆柱。
A 、B 、C 、D 、2、一个圆锥的体积是36dm 3,它的底面积是18dm 2,它的高是( )dm 。
A 、23 B 、2 C 、6 D 、183、下面( )图形是圆柱的展开图。
(单位:cm )4、下面( )杯中的饮料最多。
5、一个圆锥有( )条高,一个圆柱有( )条高。
A 、一 B 、二 C 、三 D 、无数条6、如右图:这个杯子( )装下3000ml 牛奶。
A 、能B 、不能C 、无法判断二、判断对错。
()1、圆柱的体积一般比它的表面积大。
()2、底面积相等的两个圆锥,体积也相等。
()3、圆柱的体积等于和它等底等高的圆锥体积的3倍。
()4、“做圆柱形通风管需要多少铁皮”是求这个圆柱的侧面积。
()5、把圆锥的侧面展开,得到的是一个长方形。
三、想一想,连一连。
四、填一填。
1、2.8立方米=()立方分米6000毫升=()3060立方厘米=()立方分米5平方米40平方分米=()平方米2、一个圆柱的底面半径是5cm,高是10cm,它的底面积是()cm2,侧面积是()cm2,体积是()cm3。
3、用一张长分米,宽分米的长方形铁皮制成一个圆柱,这个圆柱的侧面积最多是()平方分米。
(接口处不计)4、一个圆锥和一个圆柱等底等高,圆锥的体积是76cm3,圆柱的体积是()cm3。
5、一个圆锥的底面直径和高都是6cm,它的体积是( )cm3。
五、求下面图形的体积。
(单位:厘米)六、解决问题。
1、⑴制作这个薯片筒的侧面标签,需要多大面积的纸?⑵这个薯片筒的体积是多少?2、在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高米。