当前位置：文档之家 › 梯形、矩形渠道水力计算讲解学习

梯形、矩形渠道水力计算讲解学习

  • 格式：xls
  • 大小：137.50 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

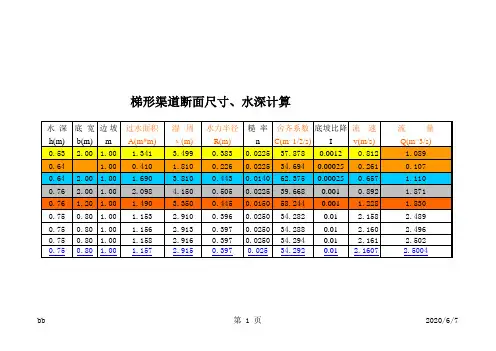
梯形、矩形渠道水力计算

梯形、矩形渠道水力计算

bb
第 3 页
2014-4-11
河道流量~水位关系曲线
水 位 h(m) 4014 4015 4016 4017 4018 4019 4020 4021 4022 4023 4024 过水面积 A(m ) 0.271729 16.396069 49.435331 100.471771 156.643397 215.447505 277.673195 342.881492 410.23577 479.724499 551.347679
梯形渠道断面尺寸、水深计算
水 深 底 宽 边坡 h(m) 0.53 0.64 0.64 0.76 0.76 0.75 0.75 0.75 0.75 b(m) m 1.00 2.00 1.00 2.00 1.00 1.20 1.00 0.80 1.00 0.80 1.00 0.80 1.00 0.80 1.00 2.00 1.00 过水面积 A(m*m) 1.341 0.410 1.690 2.098 1.490 1.153 1.156 1.158 1.157 湿 周 χ (m) 3.499 1.810 3.810 4.150 3.350 2.910 2.913 2.916 2.915 水力半径 R(m) 0.383 0.226 0.443 0.505 0.445 0.396 0.397 0.397 0.397 糙 率 n 0.0225 0.0225 0.0140 0.0225 0.0150 0.0250 0.0250 0.0250 0.025 舍齐系数 底坡比降 流75 39.668 58.244 34.282 34.288 34.294 34.292 I 0.0012 0.00025 0.00025 0.001 0.001 0.01 0.01 0.01 0.01 速 流 1.089 0.107 1.110 1.871 1.830 2.489 2.496 2.502 2.5004 量 v(m/s) 0.812 0.261 0.657 0.892 1.228 2.158 2.160 2.161 2.1607 Q(m^3/s)

流体力学辅导材料7-第七章-明渠恒定流-【教学基本要求】-1

流体力学辅导材料7-第七章-明渠恒定流-【教学基本要求】-1

流体力学辅导材料7第七章 明渠恒定流【教学基本要求】1、理解明渠分类，掌握梯形渠道和矩形渠道过流断面的水力要素计算。

2、理解明渠恒定均匀流形成条件，,掌握明渠恒定均匀流水力特征。

3、掌握明渠恒定均匀流水力计算基本公式。

4、理解水力最优断面与允许流速的概念。

5、会进行明渠恒定均匀流水力计算（求流量、底坡、断面尺寸的确定等）。

6、理解明渠恒定非均匀流形成条件及明渠恒定非均匀流水力特征。

6、理解明渠水流的流态（缓流、临界流、急流），掌握其判别标准。

7、理解断面单位能量s E 、临界水深K h 、临界底坡K i 等概念。

8、了解弗劳德数Fr 的物理意义，熟悉其数学表达式。

9、了解水跃、跌水现象和流动特征，知道水跃方程、共轭水深、水跃能量损失和跃的计算。

10、知道明渠恒定非均匀渐变流微分方程。

11、会进行棱柱形渠道水面曲线定性分析。

12、会进行棱柱形渠道恒定非均匀渐变流水面曲线计算（分段求和法）。

【学 习 重 点】1、明渠的分类，明渠恒定均匀流的水流特征，及其形成条件。

2、明渠恒定均匀流计算基本公式。

3、明渠断面形状、尺寸，底坡的设计及其水力计算。

4、缓流、急流、临界流及其判别标准。

5、断面单位能量、临界水深、临界底坡等概念。

6、跌水、水跃水流特征，共轭水深等概念。

7、棱柱形渠道恒定非均匀渐变流水面曲线的变化规律及其定性分析。

8、棱柱形渠道恒定非均匀渐变流水面曲线的计算（分段求和法）。

【内容提要和学习指导】一.概述明渠水流是指河道或渠道中水流，其自由表面为大气压，相对压强为0，亦称无压流。

本章介绍明渠的分类，明渠水流特征，及其水力计算。

本章分为两大部分：第一部分为明渠恒定均匀流。

第二部分为明渠恒定非均匀流。

这一章的基本概念较多，要多从物理意义上加以理解。

有些水力计算比较繁，如梯形断面渠道的断面尺寸的设计、共轭水深、水面曲线的计算，要求掌握其计算方法，利用相关资料会进行计算。

考核内容为基本概念和矩形断面渠道的水力计算。

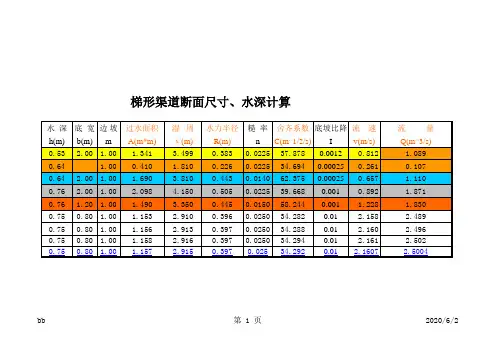
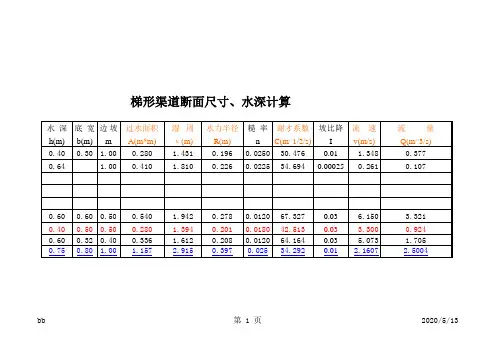
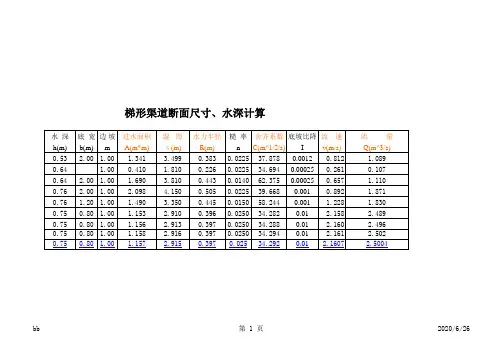
梯形、矩形渠道水力计算

梯形、矩形渠道水力计算

糙 率 n 0.081 0.081 0.081 0.081 0.081 0.081 0.081 0.081 0.081 0.081 0.081
比降 I 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083
3
量
Q(m /s) 0.08 22.27 98.45 262.85 530.44 864.78 1263.62 1741.39 2283.15 2884.78 3544.89
水位~流量关系 0.078367335302791,4014 22.2684979665597,4015 98.4472190836339,4016 262.852534592614,4017 530.436469830763,4018 864.783254675727,400 1741.39130455916,4021 2283.15020523118,4022 2884.77735399527,4023 3544.88725537302,4024
bb
第 2 页
2016/6/17
河道流量~水位关系曲线
水 位 h(m) 4014 4015 4016 4017 4018 4019 4020 4021 4022 4023 4024 过水面积 A(m ) 0.271729 16.396069 49.435331 100.471771 156.643397 215.447505 277.673195 342.881492 410.23577 479.724499 551.347679
bb
第 4 页
2016/6/17
河道流量~水位关系曲线
水 位 h(m) 4014 4015 4016 4017 4018 4019 4020 4021 4022 4023 4024 过水面积 A(m2) 0.271729 16.396069 49.435331 100.471771 156.643397 215.447505 277.673195 342.881492 410.23577 479.724499 551.347679 湿 周 χ (m) 4.18881 24.7324 41.99927 56.68853 60.01827 63.96554 68.29129 71.52681 74.59941 77.67202 80.74461 水力半径 R(m) 0.06487 0.662939 1.177052 1.772347 2.609929 3.368181 4.066012 4.793748 5.499183 6.176285 6.828291 糙 率 n 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 比降 I 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 流 量 Q(m3/s) 0.08 22.27 98.45 262.85 530.44 864.78 1263.62 1741.39 2283.15 2884.78 3544.89 水位~流量关系 0.078367335302791,4014 22.2684979665597,4015 98.4472190836339,4016 262.852534592614,4017 530.436469830763,4018 864.783254675727,4019 1263.61640298651,4020 1741.39130455916,4021 2283.15020523118,4022 2884.77735399527,4023 3544.88725537302,4024

渠道水力计算

渠道水力计算

0.068611328 9.12
8.476 0.929386 47.19416011 14.398045 3.806583286
0.068611328 9.12
8.476 0.929386 47.19416011 14.398045 3.806583286
综合糙率（n)
nmax/nmin＜1.5 nmax/nmin＞
定了渠底宽度b，设一系列h，做出K=f(h)曲线图，再由已知流量Q和底坡i算出相应的流量模数K已知，在曲线图上查出
湿周（χ）
水力半径 （R）
谢才系数 流量模数 已知流量模数
（C)
（K)
（K已知）
6.52 0.693251534 37.6306567 141.620346 18.76091434 1.453306673 47.3017302 1554.77278 23.41640786 2.049844719 50.0923003 3442.49006 27.88854382 2.58170525 52.055736 6022.18949 32.36067977 3.090169944 53.6390663 9429.14667
相对稳定断面 （β）
水深 （h）
底宽
(b)
38
0.007
0 0.0209 7.448471389 1.162294654 8.657318479
(3)实用经济断面宽深比
计算方法： （1）拟定偏离系数α：α=A经/A优（一般取α=1.01～1.4） （2）计算γ： γ=h经/h优 γ=α5/2-(α*（α4-1）)1/2 （3）计算宽深比β：β=(α*（2（1+m2)1/2-m)-m)/r2
0.0225 0.020932018 0.020932018

梯形、矩形渠道水力计算表 ——有用(算出流速和流量)

梯形、矩形渠道水力计算表 ——有用(算出流速和流量)

A(m*m) 0.151 0.392 0.280
χ (m) 1.244 1.568 1.453
R(m) 0.121 0.250 0.193
n 0.016 0.016 0.016
C(m^1/2/s) 43.975 49.606 47.499
I 0.001 0.001 0.001
v(m/s) 0.484 0.784 0.659
bb
第 2 页
2017/11/25
bb
第 3 页
2017/11/25
bb
第 4 页
2017/11/25
流
量
Q(m^3/s) 7.921 流 量
Q(m^3/s) 0.761
流
量
Q(m^3/s) 0.392 1.69 流 量 适用条件
bb
第 5 页
2017/11/25
适用条件 Q(m^3/s) 0.073 0.307 0.185 r≤0.2 r＜1.0 r≥1.0 水深h 在圆弧 段以上 -1.32
bb
第 9 页
2017/11/25
bb
第 10 页
2017/11/25
bb
第 11 页
2017/11/25
bb
第 12 页
2017/11/25
bb
第 13 页
2017/11/25
水力半径 R(m) 0.428 R(m) 0.308
糙 率 n 0.017 n 0.017
谢才系数 底坡比降 C(m^1/2/s) 51.068 C(m^1/2/s) 48.344 I 0.001 I 0.00/s) 0.968
Q(m^3/s) 1.723 Q(m^3/s) 0.702
梯形渠道断面尺寸、水深计算

梯形、矩形渠道水力计算

梯形、矩形渠道水力计算

梯形渠道断面尺寸、水深计算水深底宽边坡过水面积湿周水力半径糙率谢才系数坡比降流速流量h(m)b(m)m A(m*m)χ(m)R(m)n C(m^1/2/s)I v(m/s)Q(m^3/s) 0.400.30 1.000.280 1.4310.1960.025030.4760.01 1.3480.377 0.64 1.000.410 1.8100.2260.022534.6940.000250.2610.1070.600.600.500.540 1.9420.2780.012067.3270.03 6.150 3.321 0.400.500.500.280 1.3940.2010.018042.5130.03 3.3000.924 0.600.320.400.336 1.6120.2080.012064.1640.03 5.073 1.705 0.750.80 1.00 1.157 2.9150.3970.02534.2920.01 2.1607 2.5004说明：1、计算的范围为尾水（即尾0+000~尾0+017.5）。

2、计算时假设该渠水流为明渠均匀流进行水力计算。

3、该渠道的衬砌为浆砌块石衬砌，其糙率n值取为n=0.025。

水 深过水面积湿 周水力半径糙 率谢才系数底坡比降流 速流 量h(m)A(m*m)χ(m)R(m)n C(m^1/2/s)I v(m/s)Q(m^3/s)0.6700 1.608 3.740.42994650.022538.6117860.00120.8770 1.41030.40000.16 1.20.13333330.01259.5628140.03 3.76710.6027.0#VALUE!#VALUE!0.014#VALUE!0.0012#######VALUE!0.80000.56 2.30.24347830.01843.9006410.01 2.1662 1.21311.3800 2.208 4.360.5064220.02535.7118290.002 1.1365 2.50950.30000.090.90.10.01256.7743390.03 3.10970.27990 1.600.02500.0020.00000.00001.3770 2.2032 4.3540.50601750.02535.7070720.002 1.1359 2.50271.38002.2084.360.5064220.02535.7118290.002 1.13652.5095201882.400.401.800.70矩形渠道断面尺寸、水深计算底 宽b(m)1.601.600.301.601.60水 位湿 周水力半径糙 率比降h(m)χ(m)R(m)n I 4014 4.188810.064870.0810.0083401524.73240.6629390.0810.0083401641.99927 1.1770520.0810.0083401756.68853 1.7723470.0810.0083401860.01827 2.6099290.0810.0083401963.96554 3.3681810.0810.0083402068.29129 4.0660120.0810.0083402171.52681 4.7937480.0810.0083402274.59941 5.4991830.0810.0083402377.67202 6.1762850.0810.0083402480.744616.8282910.0810.008314.0209061270931,401561.9852860896954,4016165.499744002757,40170.0493423963017573,4014水位~流量关系795.6114.02156.643397215.447505277.673195河道流量~水位关系曲线333.978518041592,4018544.493160351384,4019795.610327806321,4020流 量Q(m 3/s)0.05A(m 2)过水面积0.27172916.39606949.435331100.471771479.724499342.881492410.235771437.541816.34551.3476792231.971437.53901810852,40221816.34129695998,40232231.96604967931,402461.99165.50333.981096.43156212984,40211096.43544.49河道流量~水位关系曲线河道流量~水位关系曲线河道流量~水位关系曲线河道流量~水位关系曲线河道流量~水位关系曲线河道流量~水位关系曲线河道流量~水位关系曲线0.2780.466.90.160.2231780.040.2975713 1.1902850.12419166860325393625640高程261577.6 470332.55293136.569967 2.054854796.280.507464530.8910 2.29723770110.9594720.8916220.58413933690.4333332860.2780.552.80.790.1076410.2780.552.80.10.73392高程45128267891096110.58120.413142775 1.250.7224030.043000高程39008400 4400 5450 646.379.27416.379474723.185 4.6378.18547220 895449 1.3842694561011121315.7-0.0079614高程4567891011121314实际堆渣量可堆渣量（万m3）（万m3）1#废石场新建矿区道路下方0.490.52103024m～3034m0.21沟谷地，但坡度较陡、坡度在30°左右。

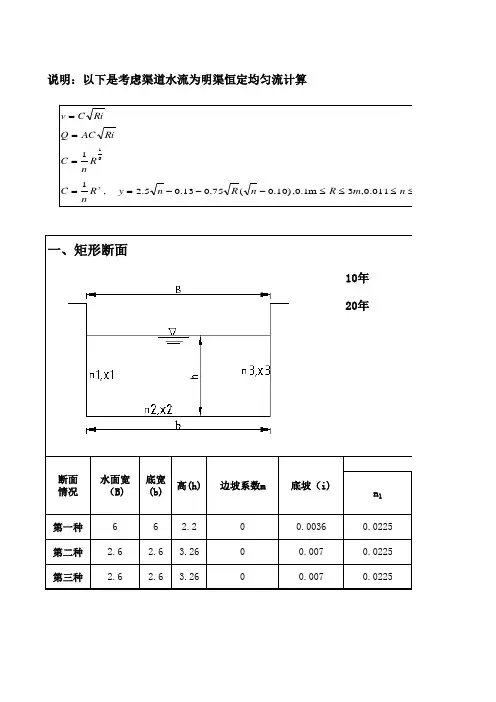
梯形、矩形渠道水力计算


流
3
量
Q(m /s) 0.08 22.27 98.45 262.85 530.44 864.78 1263.62 1741.39 2283.15 2884.78 3544.89
水位~流量关系 0.078367335302791,4014 22.2684979665597,4015 98.4472190836339,4016 262.852534592614,4017 530.436469830763,4018 864.783254675727,4019 1263.61640298651,4020 1741.39130455916,4021 2283.15020523117,4022 2884.77735399527,4023 3544.88725537302,4024
糙 率 n 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051 0.051
比降 I 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083 0.0083
高程 4 5 6 7 8 9 10 11 12 13 14
bb
第 4 页
2013-12-12
河道流量~水位关系曲线
水 位 h(m) 4014 4015 4016 4017 4018 4019 4020 4021 4022 4023 4024 过水面积 A(m ) 0.271729 16.396069 49.435331 100.471771 156.643397 215.447505 277.673195 342.881492 410.23577 479.724499 551.347679

水力学各种计算

计算方法说明明渠均匀流求正常水深程序是针对棱柱体明渠（过水断面为对称梯形或矩形）恒定均匀流，已知河床底坡i ，河床糙率n,过水断面形状（b,m ），流量Q ，求解正常水深h 0。

明渠断面示意图按照谢才公式：Ri CA =Q谢才系数：611R n=C过水断面面积：h mh b A )(+= 湿周：212m h b ++=χ 水力半径：χ/A R =由此解得正常水深：)/()12()(04.0203.0220mh b m h b iQ n +++=h算法：采用迭代法求解非线性代数方程。

1. 正常水深的迭代方程为：)/()12()(04.0203.02201n n n mh b m h b iQ n h +++=+；2.假设。

进行迭代求解h ； m h 0.100=....321000h h ⇒⇒3.迭代结束的判断依据为ε<Q Q Q /|-计算|，ε为一个小值。

求临界水深程序是针对棱柱体明渠（过水断面为对称梯形或矩形）恒定均匀流，已知过水断面形状（b,m ），流量Q ，动能校正系数α，求解临界水深hc 。

明渠断面示意图临界水深公式：0132=−=c c s B gA Q dh dE α其中，――断面单位能量。

s E 由此可得：cc B A g Q 32=α过水断面面积：h mh b A )(+= 水面宽度：mh b B 2+=由此解得临界水深： 3132])/()2()/[(c c c mh b mh b g Q h ++×=算法：采用迭代法求解非线性代数方程。

1. 临界水深的迭代方程为：3132])/()2()/[(1n n n c c c mh b mh b g Q h ++×=+； 2.假设。

进行迭代求解h ；m h c 0.10=....321c c c h h ⇒⇒3.迭代结束的判断依据为ε<+n n n c c c h h h /|1－|并且ε<++11/|n n n c c c h h h －|，ε为一个小值。

U形渠道与梯形_矩形渠道衬砌工程量的分析比较_潘起来


32
[ 2]
青海师范大学学报( 自然科学版 )
2004 年
水深和渠宽 , 进而计算湿周 x . 见表 1.
表1 U 形渠 i = 0 001 Q 0 0 5 13 12 0 1 13 12 0 3 13 12 n= 0 015 D 1 17 0 871 0 792 1 518 1 13 1 028 2. 293 1 705 1 551 xu 1 838 1 949 2 036 2 358 2 53 2 64 3 602 3 81 3 988 1 10 1. 10 3 85 0 73 0 73 2 555 0 56 0 56 1 96 h M = 0 75 b Q 3m 3 s 时 , U 形渠和梯形渠比较表 梯形渠 i = 0 001 x梯 梯形渠 i = 0 001 b x梯
2/ 5
- D/3
2/ 5
表3 X 0 1 3 1 2 1 0 418D 0 428D 0 433D 0 440D
U 形渠与矩形渠比较表
= 0. 427D 3/ 5 X 2 = 0. 526 D [ 1. 667D + 2 D / 3= 0. 428 D 精确到 0 001D , X = 0 428 D ;
Q > 3m 3 s 时 , U 形渠和梯形渠比较表 梯形渠 i = 0 001 h 备 K( %) 17. 2 0. 4 2. 4 0. 96 5。 11 10. 6 5. 8 23 8 注
表2 U 形渠 i = 0 001 n= 0 015 Q 0 5 13 12 0 10 13 12 0 50 13 12 0 100 13 12 D 2. 778 2. 07 1. 88 3 60 2 678 2 436 6 59 4 898 4 46 8 54 6 35 5 779 xu 4. 363 4. 62 4. 83 5 658 5 99 6 26 10 35 10 96 11 455 13 417 14 21 14 85

梯形类渠道水力最佳断面统一公式的推求


" ! < = ’ # ; # 7 #> & ( ; ’ #> ? $ ’ % ’
" 以上各式中， <# #> < $$ ; #’A ( " ) * $+ 1*’ 其余各变量的含义参见图 $、 图 ’、 图 ( 中所标 。 梯形渠道的水力最佳断面可以通过对式 # $ & 、 式 ・ !・
第 " 期 # 总第 $%& 期 ’ (&&) 年 $& 月 #(’ 求
* ( ’・ & !N
# ($ ’
$ S # " #T E " # E " ’ # ’ E $ ’ ( W # " W ( # ’ U &( # (( ’ (
!"#$%&’$() (* +)$*$", -./&’$() *(# 0"1’ 23,#&/4$5 6"5’$() (* 7#&8"9($, : ’38", ;<&))"4 3+45 6745./+ =>1’#&5’? -89: ;/;7< =7<9>7: .87 ?49@97= 7A?/.9+4 @+< .87 B7:. 8C=<?092 :72.9+4 +@ .</;7D+9= E .C;7= 28/4470F G8928 9420?=7 .87 :./4=/<= .</;7D+9=/0 28/4470F .</;7D+9=/0 28/4470 G9.8 2?<>7= B+..+H /4= .</;7D+9=/0 28/4470 G9.8 2?<>7= :0+;7.+7, @"3 A(#,1I J8/4470 -</;7D+9= J?<>7= K+..+H J?<>7= L0+;7 -+7 K7:. MC=</?092 L72.9+4
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

适用条件
0.073 0.307 0.185
r≤0.2 r＜1.0 r≥1.0
水深h 在圆弧 段以上
第4页
2020/7/9
算
流量 Q(m^3/s)
0.202
bb
第5页
2020/7/9
0.001
0.784
弧形渠道断面尺寸、水深计算
外倾角
过水面积 湿 周 水力半径 糙 率 谢才系数 底坡比降 流 速
弧度rad 角度° A(m*m)
χ(m)
R(m)
n
C(m^1/2/s)
I
v(m/s)
0.248 15.00
0.151
1.244
0.121
0.016 43.975
0.001
0.484
0.364 22.00
A(m*m)
χ(m)
R(m)
n
C(m^1/2/s)
I
0.291
1.400
0.208
0.016 48.112
0.001
流速 v(m/s) 0.694
bb
第2页
2020/7/9
bb
第3页
2020/7/9
算 算 算
bb
流量 Q(m^3/s)
0.680
流量 Q(m^3/s)
0.392
流量 Q(m^3/s)
0.392
1.568
0.250
0.016 49.606
0.001
0.784
0.496 30.00
0.280
1.453
0.193
0.016 47.499
0.001
0/7/9
水深 h(m) 0.5000
半径 R(m) 0.40
U型渠道断面尺寸、水深计算
过水面积 湿 周 水力半径 糙 率 谢才系数 底坡比降
I
v(m/s)
1.00
0.750
2.414
0.311
0.016 51.435
0.001
0.907
矩形渠道断面尺寸、水深计算
底宽
过水面积 湿 周 水力半径 糙 率 谢才系数 底坡比降 流 速
b(m)
A(m*m)
χ(m)
R(m)
n
C(m^1/2/s)
I
v(m/s)
1.00
0.500
2.000
0.250
0.016 49.606
水深 h(m) 0.50
水深 h(m) 0.50
水深 h(m) 0.5000 0.5000 0.5000
底宽 b(m) 1.00
半径 R(m) 0.20 0.50 0.35
梯形渠道断面尺寸、水深计算
边坡
过水面积 湿 周 水力半径 糙 率 谢才系数 底坡比降 流 速
m
A(m*m)
χ(m)
R(m)
n
C(m^1/2/s)