渠道断面计算--矩形断面

P.O.Box21802 - 00505, NairobiTel：00254-20-5201783E-mail:*************; *********************Fax：00254-20-2667177------------------------------------------------------------------------------------------------------------------------------------------MURUNYDAM单箱涵过流水力学计算[断面简图 ][基本参数]渠道类型: 清水渠道水流运动状态:均匀流计算目标: 计算流量断面类型: 矩形断面渠道的等值粗糙高度:1.800(mm)水的运动粘滞系数: 1.011×10^-6(m2/s)计算谢才系数公式采用manning公式不验算不冲不淤流速:渠道底坡： 0.0117[几何参数]渠道底宽b: 2.500(m)P.O.Box21802 - 00505, NairobiTel：00254-20-5201783E-mail:*************; *********************Fax：00254-20-2667177------------------------------------------------------------------------------------------------------------------------------------------渠道深度H: 2.250(m)渠道中水深h0: 2.250(m)[糙率参数]粗糙的砼面糙率n: 0.01700[ 计算过程 ]一、假定水流处于:水力粗糙区。

渠道的过水断面面积：5.625(m2)渠道断面的湿周：7.000(m)渠道断面的水力半径：0.804(m)渠道断面的水面宽：2.500(m)二、计算流量。

第一章 绪论答案1-1．20℃的水2.5m 3，当温度升至80℃时，其体积增加多少？ [解] 温度变化前后质量守恒，即2211V V ρρ= 又20℃时，水的密度31/23.998m kg =ρ 80℃时，水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆ 1-2．当空气温度从0℃增加至20℃时，运动粘度ν增加15%，重度γ减少10%，问此时动力粘度μ增加多少（百分数）？ [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%。

1-3．有一矩形断面的宽渠道，其水流速度分布为μρ/)5.0(002.02y hy g u -=，式中ρ、μ分别为水的密度和动力粘度，h 为水深。

试求m h 5.0=时渠底（y =0）处的切应力。

[解] μρ/)(002.0y h g dy du -=)(002.0y h g dydu -==∴ρμτ 当h =0.5m ，y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4．一底面积为45×50cm 2，高为1cm 的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s ，油层厚1cm ，斜坡角22.620 （见图示），求油的粘度。

[解] 木块重量沿斜坡分力F 与切力T 平衡时，等速下滑y u AT mg d d sin μθ== 001.0145.05.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg =s Pa 08376.0⋅ 1-5．已知液体中流速沿y 方向分布如图示三种情况，试根据牛顿内摩擦定律y ud d μτ=，定性绘出切应力沿y[解]1-6．为导线表面红绝缘，将导线从充满绝缘涂料的模具中拉过。

库灌区节水改造中渠道衬砌断面的选择随着经济的不断发展和人口的增长，对水资源的需求也在不断增加，而水资源的供给却并没有相应增加，特别是在干旱缺水地区，节水成为亟待解决的问题。

库灌区是我国开发水利工程中的一种重要形式，对于节约水资源、提高农田水利设施的利用效率具有重要意义。

而在库灌区节水改造中，渠道衬砌断面的选型是至关重要的一环，对于渠道的运行效率、水资源的利用效率以及工程的运行维护都有着重要的影响。

本文将对库灌区节水改造中渠道衬砌断面的选择进行讨论和探究。

库灌区节水改造的重要性库灌区节水改造，是指通过对水利工程设施进行优化升级，以减少水资源的浪费和提高水资源的利用效率。

这不仅是对水资源的合理利用，更是对节约国家资源和保护生态环境的重要举措。

而库灌区作为我国一项重要的灌区形式，在节水改造中具有重要地位和作用。

一方面，库灌区的节水改造可以提高渠道输水效率，减少水漏损。

目前我国许多库灌区的灌溉渠道存在着渗漏严重、输水效率低下的问题，导致了大量的水资源浪费。

通过对渠道进行衬砌改造，可以有效减少渠道的渗漏和水源的浪费，提高输水效率。

库灌区的节水改造不仅有利于提高灌区水利工程的运行效率，减少水资源的浪费，还有利于提高农田的水分利用效率，减少用水量，具有重要的经济和环境效益。

而渠道衬砌断面的选择作为库灌区节水改造的重要环节，对于节水改造的效果有着重要的影响。

渠道衬砌断面的选择原则在库灌区节水改造中，渠道衬砌断面的选择是一个复杂的问题，需要综合考虑地质条件、水文条件、工程条件、经济条件等多个因素。

在进行渠道衬砌断面的选择时，需要遵循以下几个原则：1. 经济合理原则。

渠道衬砌断面的选择首先需要考虑其经济合理性，包括施工成本、后期维护成本等因素。

在保证渠道衬砌的质量和安全的前提下，需要尽量选择经济成本较低的衬砌材料和结构形式，以确保节水改造的经济效益。

2. 安全可靠原则。

渠道衬砌断面的选择需要考虑到工程的安全和稳定性，尤其是在地质条件复杂、水文条件较差的区域，需要更加重视工程的安全可靠性，确保衬砌结构不受流水侵蚀和冲刷，保证渠道的长期稳定运行。

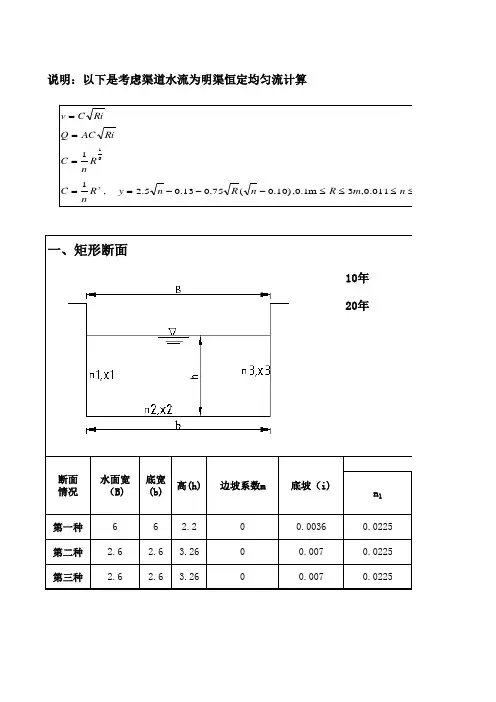
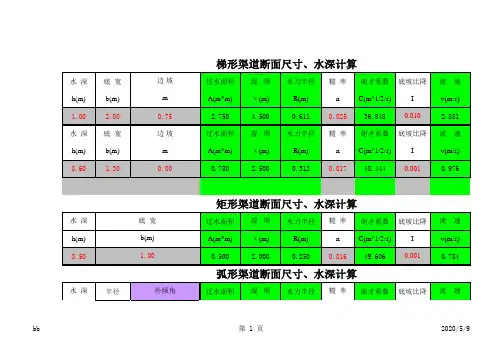
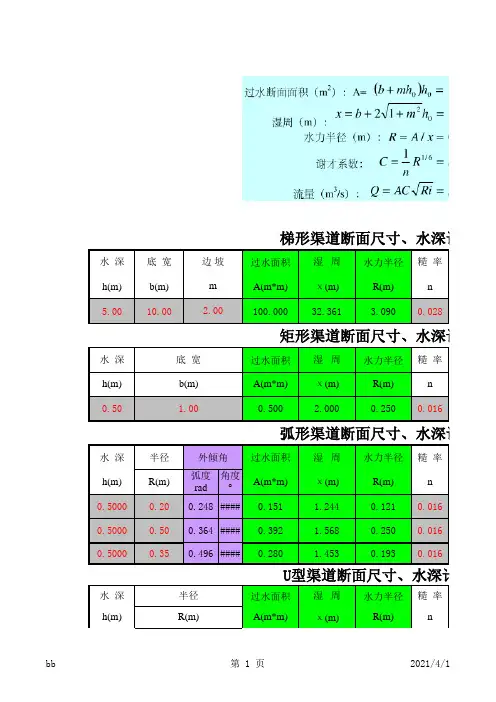
灌溉渠道的断面类型及应用灌溉渠道的断面类型及应用灌溉渠道是农田灌溉系统中的重要组成部分，起到引水、输水和调节水流的作用。

根据渠道的用途和地形条件，灌溉渠道的断面类型各有特点。

下面将介绍四种常见的灌溉渠道断面类型及其应用。

1. 矩形断面矩形断面是最常见的灌溉渠道断面类型，通常由水平底床和垂直侧壁组成，底宽和侧壁高度相对较大。

这种断面类型适用于大断面流量较大的主干渠，能够承载较大的水流压力。

矩形断面的优点是结构简单，易于施工和维护，且能够保持水流稳定。

因此，矩形断面常用于主干渠和干净水渠等水流较大的渠道。

2. 梯形断面梯形断面是较常用的灌溉渠道断面类型之一，其底床呈梯形状，底宽较矩形断面小，侧壁高度较矩形断面高。

梯形断面适用于地势较陡且要求流速较快的地区。

由于底宽较小，梯形断面渠道的流速较快，能够有效地减少泥沙淤积。

此外，梯形断面还可以减小渠道的水力半径，降低渠岸侵蚀的风险。

因此，梯形断面常用于次要渠道和支渠等较小流量的渠道。

3. V形断面V形断面的底床呈V形，两侧是倾斜的边坡，适用于地势较陡或渠道长度较长的地区。

V形断面渠道具有较小的水力半径和较快的流速，能够减小流量对渠道的摩擦阻力，降低能量损失。

此外，V形断面还能够减小渠道面积，降低渠道建设的成本。

因此，V形断面常用于山区的灌溉渠道，能够有效地输送水流，提高灌溉效果。

4. 圆形断面圆形断面是另一种常见的灌溉渠道断面类型，其底床呈半圆形，适用于地势平坦或者有大量泥沙的地区。

圆形断面渠道的优点是水力半径大，摩擦阻力小，能够保持水流稳定，减少能量损失。

此外，圆形断面还能够减小泥沙淤积的风险，提高渠道的通水能力。

因此，圆形断面常用于平原地区的灌溉渠道和泥沙含量较高的区域。

总之，灌溉渠道的断面类型根据不同的要求和地理条件选择不同的形式。

矩形断面适用于大断面流量较大的主干渠，梯形断面适用于地势陡的次要渠道，V形断面适用于地势陡或渠道长度长的山区渠道，圆形断面适用于地势平坦或泥沙多的平原地区。

渠道水力计算类型在水利工程中，梯形渠道应用最为广泛，因而后面以梯形断面为代表，讨论渠道的水力计算方法。

因明渠流量计算公式32352132==x A n i i R n A Q ，将梯形的面积h mh b A )(+=、湿周212m h b ++=χ代入上式得[][]32235+12++=mh b h mh b n i Q )( (6-17) 则),,,,(=i n m h b f Q ，这说明，梯形断面水力计算存在着（Q 、b 、h 、m 、n 、i ）六个变量。

通常渠道的边坡系数m 和糙率系数n ，可由渠的地质情况、施工条件、护面材料等实测确定，或由经验查表确定。

则渠道的水力计算主要是流量计算、正常水深计算、渠宽度计算及渠底坡度计算。

明渠均匀流的水力计算问题,可分为两大类：一类是对已建成的渠道进行计算，如校核流速、流量、糙率和底坡；另一类是按要求设计新渠道，如确定底宽、水深、底坡、边坡系数或超高等。

一、已成渠道的水力计算已成渠道的水力计算任务是校核过水能力及流速，或由实测过水断面的流量反推粗糙系数和底坡。

下面以例题形式来说明。

1. 流量和流速的校核【例6-3】 某灌溉工程粘土渠道，总干渠全长70km ，糙率n =0.028，断面为梯形，底宽为8m ，边坡系数m = 1.5，底坡i=1/8000，设计流量Q 为40m 3/s 。

试校核当水深为4m 时，能否满足通过设计流量的要求。

解： (1) 流量校核由于渠道较长，断面规则，底坡和糙率固定，故可按明渠均匀流计算。

因： 4)45.18()(⨯⨯+=+=h mh b A = 56（m 2）42.22=5.1+1×4×2+8=+12+=22m h b x （m ）水力半径： 42.2256==x A R = 2.498 m 谢才系数： 6161498.2028.011⨯==R n C = 41.6 m 1/2 / s流 量 =)8000/1(×498.2×6.41×56==Ri AC Q 41.17 m 3 /s(2) 流速较核：74.0=5617.41==A Q v （m/s ）>不淤v =0.5m/s查表6-4粘土渠道，不冲流速允许值为（0.75～0.85）m/s,水力半径为2.498m, 则实际允许流速为()=498.2×)85.0~75.0(==41αR 表不冲v v 0.942～1.07m/s因计算流量大于设计流量,则满足能过设计流量的要求；实际流速满足不冲、不淤允许流速要求。

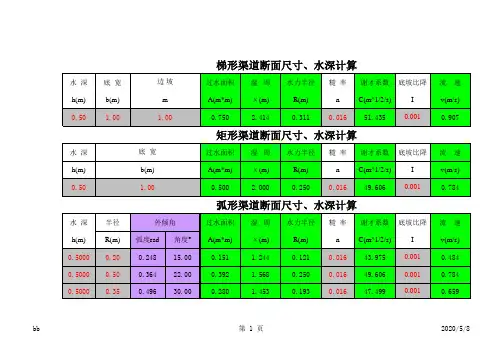
宽顶堰流的水力计算如图所示，水流进入有底坎的堰顶后，水流在垂直方向受到堰坎边界的约束，堰顶上的过水断面缩小，流速增大，势能转化为动能。

同时堰坎前后产生的局部水头损失，也导致堰顶上势能减小。

所以宽顶堰过堰水流的特征是进口处水面会发生明显跌落。

从水力学观点看，过水断面的缩小，可以是堰坎引起，也可以是两侧横向约束引起。

当明渠水流流经桥墩、渡槽、隧洞〈或涵洞)的进口等建筑物时，由于进口段的过水断面在平面上收缩，使过水断面减小，流速加大，部分势能转化为动能，也会形成水面跌落，这种流动现象称为无坎宽顶堰流，仍按宽顶堰流的方法进行分析、计算。

（一）流量系数宽顶堰的流量系数取决于堰的进口形状和堰的相对高度，不同的进口堰头形状，可按下列方法确定。

1、进口堰头为直角(8-22)2、进口堰头为圆角(8-23)3、斜坡式进口流量系数可根据及上游堰面倾角由表选取。

在公式（8-22）、（8-23）中为上游堰高。

当≥3时，由堰高引起的水流垂向收缩已达到相当充分程度，故计算时将不考虑堰高变化的影响，按=3代入公式计算值。

由公式可以看出，宽顶堰的流量系数的变化范围在0.32～0.385之间，当=0时，=0.385，此时宽顶堰的流量系数值最大。

比较一下实用堰和宽顶堰的流量系数，我们可以看到前者比后者大，也就是说实用堰有较大的过水能力。

对此，可以这样来理解：实用堰顶水流是流线向上弯曲的急变流，其断面上的动水压强小于按静水压强规律计算的值，即堰顶水流的压强和势能较小，动能和流速较大，故过水能力较大；宽顶堰则因堰顶水流是流线近似平行的渐变流，其断面动水压强近似按静水压强规律分布，堰顶水流压强和势能较大，动能和流速较小，故过水能力较小。

（二）侧收缩系数宽顶堰的侧收缩系数仍可按公式（8-21）计算。

（三）淹没系数当堰下游水位升高到影响宽顶堰的溢流能力时，就成为淹没出流。

试验表明：当≥0.8时，形成淹没出流。

淹没系数可根据由表查出。

无坎宽顶堰流在计算流量时，仍可使用宽顶堰流的公式。

基于公式覆盖度的矩形渠道收缩断面水深计算赵延风;洪安宇;王正中【摘要】In order to improve the application scope of water depth formula at contracted section, firstly by simplifying the bas-ic water depth equation of contracted section in rectangular channel, we obtain the non-dimensional depth iteration equation, then replacing the cubic equation by simple unary quadratic equation and taking the root of unary quadratic equation as the initial value of the iteration equation, so the water depth calculation equation can be obtained consequently. It shows that when the non-dimensional depth at contracted section is less than 0. 6, the maximum relative error is 0. 15%. This equation has simple form, high accuracy and wide application range, which provides a new calculation method of water depth at contracted section un-der special conditions.%为了适当提高收缩断面水深公式的适用范围，通过对矩形渠道收缩断面水深的基本方程进行化简，得到无量纲水深迭代方程，随后采用一元二次方程替代矩形收缩断面水深的一元三次方程，最后将二次方程的解代入迭代方程中得到无量纲收缩断面水深的计算公式。