电阻的串联与并联关系
- 格式:docx
- 大小:37.07 KB
- 文档页数:3
串、并联电路中的电阻关系(基础)责编:冯保国【学习目标】1.能根据欧姆定律以及电路的特点,得出串、并联电路中电阻的关系。
2.理解欧姆定律,能运用欧姆定律进行简单的计算。
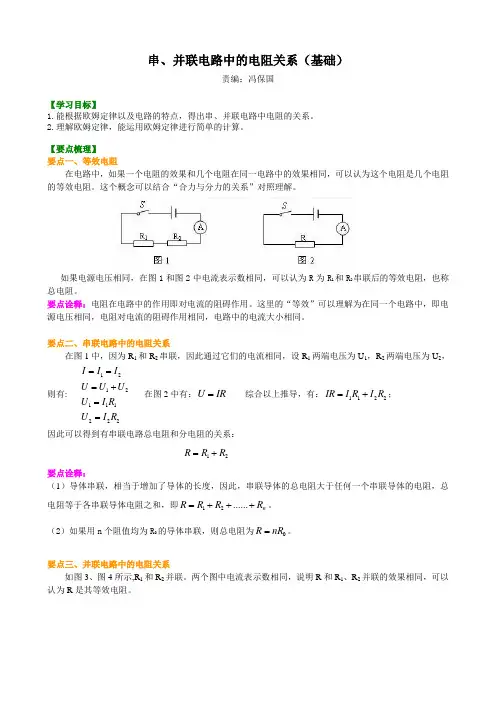
【要点梳理】要点一、等效电阻在电路中,如果一个电阻的效果和几个电阻在同一电路中的效果相同,可以认为这个电阻是几个电阻的等效电阻。
这个概念可以结合“合力与分力的关系”对照理解。
如果电源电压相同,在图1和图2中电流表示数相同,可以认为R 为R 1和R 2串联后的等效电阻,也称总电阻。
要点诠释:电阻在电路中的作用即对电流的阻碍作用。
这里的“等效”可以理解为在同一个电路中,即电源电压相同,电阻对电流的阻碍作用相同,电路中的电流大小相同。
要点二、串联电路中的电阻关系在图1中,因为R 1和R 2串联,因此通过它们的电流相同,设R 1两端电压为U 1,R 2两端电压为U 2,则有:1212111222I I I U U U U I R U I R ===+== 在图2中有:U IR = 综合以上推导,有:1122IR I R I R =+;因此可以得到有串联电路总电阻和分电阻的关系:12R R R =+要点诠释:(1)导体串联,相当于增加了导体的长度,因此,串联导体的总电阻大于任何一个串联导体的电阻,总电阻等于各串联导体电阻之和,即12......n R R R R =+++。
(2)如果用n 个阻值均为R 0的导体串联,则总电阻为0R nR =。
要点三、并联电路中的电阻关系如图3、图4所示,R 1和R 2并联。
两个图中电流表示数相同,说明R 和R 1、R 2并联的效果相同,可以认为R 是其等效电阻。
在图3中,有 1212111222=I I I U U U U I R U I R =+===在图4中,有:UI R=综合以上推导,有1212U U U R R R =+;即:12111R R R =+ , 1212R R R R R =+要点诠释:(1)导体并联,相当于增大了导体的横截面积,因此,并联导体的总电阻小于任何一个并联导体的电阻,总电阻的倒数等于各并联导体电阻的倒数之和,即121111.....nR R R R =+++。


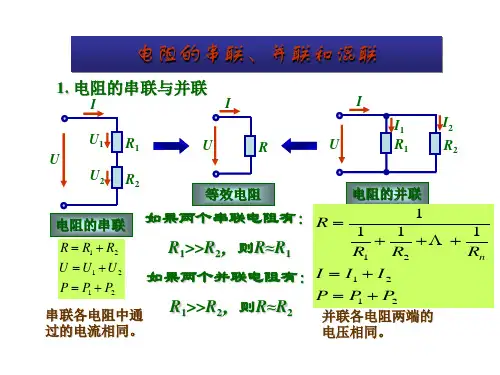
电阻串联与并联电阻串联和并联是电路中常见的两种连接方式,它们在电路中起到不同的作用。
本文将对电阻串联和并联进行详细说明,以帮助读者更好地理解这两种连接方式的特点和应用。
一、电阻串联电阻串联指的是将多个电阻依次连接在一起,使它们按照顺序形成一个电路。
在电路中,电流通过每个电阻时都要经过其他电阻,这样电阻的总阻值相当于各个电阻之和。
电阻串联的特点如下:1. 电流在串联电阻中保持连续性,即通过电路的总电流等于通过每个电阻的电流之和。
2. 电阻串联时,电压在各个电阻上分担。
根据欧姆定律,电压和电阻成正比,所以总电压等于各个电阻电压之和。
3. 串联电阻的总阻值等于各个电阻阻值之和。
即R总 = R1 + R2 +R3 + ... + Rn。
举个例子来说明电阻串联的应用。
假设我们有三个电阻分别为R1、R2和R3,在一个串联电路中连接起来。
当电流通过这个电路时,会按照电流的路径逐个通过R1、R2和R3,电阻之和即为总阻值。
这种方式可以用于控制电流的大小,实现不同电阻值的组合,例如电压分压器。
二、电阻并联电阻并联指的是将多个电阻同时连接在一起,使它们形成一个分支,这些分支再汇集到一个点上。
在并联电路中,每个电阻之间具有相同的电压差,而整个电路中的总电流等于各个分支电流之和。
电阻并联的特点如下:1. 电压在并联电阻中保持相同,即通过每个电阻的电压相等。
2. 电流在各个分支中分担,根据欧姆定律,电流和电阻成反比,所以总电流等于各个分支电流之和。
3. 并联电阻的总阻值可以通过公式1/R总 = 1/R1 + 1/R2 + 1/R3 + ...+ 1/Rn 计算得到。
举个例子来说明电阻并联的应用。
假设我们有三个电阻分别为R1、R2和R3,并行连接在一个电路中。
当电流通过这个电路时,每个电阻内的电流相等,而总电流等于各个分支电流之和。
这种方式可以用于增大电路的容量,例如在家庭用电中,将多个电器并联将使电流分散,减轻电网的负担。

电阻在串联和并联中的规律和公式摘要:I.电阻串联规律和公式A.串联电路电流处处相等B.串联电路总电压等于各支路电压之和C.串联电路总电阻等于各电阻的和II.电阻并联规律和公式A.并联电路电压处处相等B.并联电路总电流等于各支路电流之和C.并联电路总电阻的倒数等于各电阻阻值的倒数之和正文:电阻是电路中的一种基本元件,它在电路中起到阻碍电流通过的作用。
在电路分析中,我们常常需要计算电阻的串联和并联等效电阻,以便于后续的电路分析和设计。
下面我们来探讨一下电阻在串联和并联中的规律和公式。
首先,我们来看电阻串联的规律和公式。
在电阻串联电路中,电阻器依次连接起来,电流需要通过每个电阻器。
根据欧姆定律,电阻两端的电压与电阻成正比,通过电阻的电流与电阻成反比。
因此,我们可以得出以下结论:A.串联电路电流处处相等。
因为电流在电路中是连续的,所以通过每个电阻器的电流都相等。
B.串联电路总电压等于各支路电压之和。
根据基尔霍夫定律,电路两端的电压之和等于零,所以串联电路的总电压等于各电阻器两端的电压之和。
C.串联电路总电阻等于各电阻的和。
因为在串联电路中,电流需要通过每个电阻器,所以总电阻等于各电阻器的电阻值之和。
接下来,我们来看电阻并联的规律和公式。
在电阻并联电路中,电阻器分别连接在电路的两端,电压相同。
根据欧姆定律,电阻两端的电压与电阻成正比,通过电阻的电流与电阻成反比。
因此,我们可以得出以下结论:A.并联电路电压处处相等。
因为在并联电路中,电阻器分别连接在电路的两端,所以电压相同。
B.并联电路总电流等于各支路电流之和。
根据基尔霍夫定律,电路中的电流之和等于零,所以并联电路的总电流等于各电阻器中的电流之和。
C.并联电路总电阻的倒数等于各电阻阻值的倒数之和。
因为在并联电路中,电压相同,所以根据欧姆定律,总电阻的倒数等于各电阻阻值的倒数之和。

串联和并联是电路中常见的两种连接方式,它们在电流、电压和电阻之间有着不同的关系。
下面我们来详细了解一下串联和并联的电流、电压和电阻的关系。
一、串联电路的电流、电压和电阻关系1. 串联电路的电流:在串联电路中,电流只有一条路径可走,因此串联电路中的电流是相等的。
也就是说,串联电路中每个电阻上的电流都相同。
2. 串联电路的电压:在串联电路中,各个元件的电压之和等于总电压,即串联电路中的电压是相加的。
这是由基尔霍夫电压定律可得出的结论。
3. 串联电路的电阻:在串联电路中,各个电阻直接相加得到总电阻。
这也是由基尔霍夫电流定律可得出的结论。
二、并联电路的电流、电压和电阻关系1. 并联电路的电流:在并联电路中,电流可选择不同的路径进行流动,因此并联电路中的电流是分流的,即各个支路上的电流之和等于总电流。
2. 并联电路的电压:在并联电路中,各个支路上的电压相等,等于总电压。
也就是说,在并联电路中,各个支路上的电压相同。
3. 并联电路的电阻:在并联电路中,各个支路的电阻经过计算得到并联后的总电阻。
计算方式是利用电阻公式的倒数之和再取倒数。
三、串联和并联电路的不同之处1. 串联电路中的电流相等,电压相加,电阻直接相加;而并联电路中的电流分流,电压相等,电阻取倒数相加再取倒数。
2. 串联电路中的总电阻大于任意一个电阻的值,而并联电路中的总电阻小于任意一个电阻的值。
3. 串联电路中的总电压等于各个元件电压之和,而并联电路中的总电压等于各个支路的电压值。
串联和并联的电流、电压和电阻之间有着微妙的关系。
在实际应用中,根据不同的需求和情况,选择合适的串联或者并联连接方式来构建电路,是非常重要的。
对于电流、电压和电阻的关系要有清晰的理解,才能更好地分析和设计电路。
四、串并联混合电路的分析除了纯粹的串联电路和并联电路之外,还有一种常见的电路连接方式,即串并联混合电路。
在串并联混合电路中,电路中既有串联连接,又有并联连接。
这种情况下,需要对电流、电压和电阻进行更为复杂的分析。

《聊聊串并联中电阻的关系》嘿,朋友!今天咱来唠唠串并联中电阻的关系。
这电阻啊,在电路里可重要了呢。
咱先说说串联吧。
啥是串联呢?就好比一群小伙伴手拉手排成一队。
在串联电路里,电阻们就像这些小伙伴一样,一个挨着一个。
那这时候电阻会有啥变化呢?嘿,你瞧,这时候总电阻就等于各个电阻之和。
比如说,有一个电阻是 3 欧姆,另一个是 5 欧姆,那它们串联起来,总电阻就是 3 加5,等于8 欧姆。
这就像小伙伴们一起使劲,力量就变大了一样。
再说说并联。
并联呢,就像是小伙伴们分成了几队,同时在干活。
在并联电路里,电阻们也有自己的特点。
总电阻的倒数等于各个电阻的倒数之和。
哎呀,听起来有点绕是不是?咱打个比方,有两个电阻,一个是 4 欧姆,一个是 6 欧姆。
咱先算出它们的倒数,4 欧姆的倒数是1/4,6 欧姆的倒数是1/6。
然后把这两个倒数加起来,得到的和再求倒数,就是并联后的总电阻啦。
算出来大概是2.4 欧姆。
这就像小伙伴们一起合作,效率就提高了呢。
那为啥会有这样的关系呢?咱可以这么想啊。
在串联的时候,电流只有一条路可走,就得挨个经过这些电阻,所以电阻就累加起来了。
而在并联的时候呢,电流可以分成好几路走,就像有好多小帮手一起帮忙,所以总电阻就变小了。
这串并联中电阻的关系可重要了呢。
在我们生活里也有很多地方能用到。
比如说家里的电器啊,有时候它们就是并联在电路里的,这样就算一个坏了,其他的还能正常工作。
要是不明白这电阻的关系,那电器出了问题可就不好修啦。
嘿嘿,现在你对串并联中电阻的关系有点了解了吧?下次看到电路的时候,你就可以想想这些电阻是怎么串并联的,它们的关系又是啥样的。

电路中的串联与并联关系在电路中,串联与并联是常见的两种连接方式。
它们在电路中起着不同的作用和性质,对电流、电压及电阻等有着重要的影响。
本文将深入探讨电路中的串联与并联关系,并分析它们在电路中的应用。
一、串联电路串联电路指的是将多个电子组件或元件依次连接在同一条电路中,电流只能沿一个路径流动的电路。
在串联电路中,电流在电路中的各个电子元件中依次流动,电流强度在整个电路中是相等的,而电压则分配给各个电子元件。
电子元件之间是串行连接的,即各元件之间的正极与负极相连。
串联电路的特点是:1. 电流在串联电路中保持不变,各个元件之间的电流强度相等;2. 电压在串联电路中分配给各个元件,电压总和等于电源电压;3. 串联电路中的元件电阻相加,即串联电阻等于各个元件电阻之和。
串联电路的应用非常广泛。
例如,家庭中的电线路常采用串联电路,各个电器都依次连接在同一条电路中。
此外,串联电路还常用于各种电子设备中,如电视、收音机和计算机等。
二、并联电路并联电路指的是将多个电子组件或元件并排连接在电路中,每个元件之间同时连接在电源的正极和负极上。
在并联电路中,电流在各个电子元件之间分流,而电压在整个电路中保持不变。
并联电路的特点是:1. 电流在并联电路中分流,各个元件之间的电流强度之和等于总电流;2. 电压在并联电路中相同,各个元件之间的电压相等于总电压;3. 并联电路中的元件电阻之和的倒数等于各个元件电阻倒数之和的倒数。
即并联电阻等于各个元件电阻的倒数之和的倒数。
并联电路在生活中也有许多应用。
例如,房间中的灯光常采用并联电路,每个灯泡均连接在同一电源上。
此外,电路中的开关、插座等也常采用并联电路。
三、串联与并联的应用比较串联和并联是电路中常用的两种连接方式。
它们在不同的应用场景中有不同的优势。
1. 串联电路的优势:- 串联电路可以根据需要将多个电子元件连接起来,形成复杂的电路结构;- 串联电路的电压分配给各个电子元件,从而使得各个元件能够获得所需的电压;- 串联电路可以根据各个元件的特性进行精确的电流控制。

电阻的串联和并联知识点一:;:电阻的串联有以下几个特点:(指R1、R2串联,串得越多,总电阻越大)①电流:I=I1=I2(串联电路中各处的电流相等)②电压:U=U1+U2(串联电路中总电压等于各部分电路电压之和)③电阻:R=R1+R2(串联电路中总电阻等于各串联电阻之和);如果n个等值电阻(R)串联,则有R总=nR注:总电阻比任何一个分电阻都大,其原因是电阻串联相当于增加了导体的长度;④分压作用:U1/U2=R1/R2(阻值越大的电阻分得电压越多,反之分得电压越少)⑤比例关系:电流:I1∶I2=1∶1例题:电阻为12Ω的电铃正常工作时的电压为6 V,若把它接在8 V的电路上,需要给它串联一个多大的电阻?(要求画出电路图,在图上标出有关物理量)例题:把电阻R1=20Ω与电阻R2=15Ω串联起来接入电路中,流过R1、R2的电流之比是__________,R1、R2两端的电压之比是_____________。
例题:如图所示,电源电压为10V,闭合开关S后,电流表、电压表的示数分别为O.5A和6V。
求:(1)通过R1的电流I1是多少?(2)马平同学在求R2的电阻值时,解题过程如下:根据欧姆定律:R2=U/I=6V/0.5A=12Ω请你指出马平同学在解题过程中存在的错误,并写出正确的解题过程。
练习1.电阻R1和R2串联后接在电压为6 V的电源上,电阻R1=2Ω,R2=4Ω,求:(1)总电阻. (2)R1两端的电压.(要求画出电路图,在图上标出有关物理量)2.如图所示的电路中,若电源电压保持6 V不变,电阻R1=10Ω,滑动变阻器R2的变化范围是O~20Ω.求:(1)欲使电压表的示数为4 V,则此时电流表的示数为多大?滑动变阻器连入电路的电阻是多大?(2)当滑动变阻器连人电路的电阻为20Ω时,电流表、电压表的示数分别是多大?3.把电阻R1=5Ω与电阻R2=15Ω串联起来接入电路中,流过R1、R2的电流之比是__________,R1、R2两端的电压之比是___________________。

欧姆定律是电学中一个重要的基本定律,描述了电压、电流和阻抗之间的关系。
而串联和并联规律则是指在电路中电阻或其他负载组合的方式。
下面是关于欧姆定律、串联规律和并联规律的总结:
1. 欧姆定律(Ohm's Law):欧姆定律表明电路中的电流(I)与电压(V)和电阻(R)之间存在线性关系。
根据欧姆定律,电流(I)等于电压(V)与电阻(R)的比值,即I = V/R。
这意味着,当电压保持不变时,电流随着电阻的增加而减小;当电阻保持不变时,电流随着电压的增加而增加。
2. 串联规律:在电路中,当多个电阻或负载连接在一起形成串联连接时,它们依次连接在一起,形成一个电流沿着这些负载依次流动的电路。
根据串联规律,串联电阻的总电阻等于各个电阻之和,即Rt = R1 + R2 + R3 + ...。
而串联电路中的电流保持不变,即各个电阻上的电流相等。
3. 并联规律:在电路中,当多个电阻或负载并联连接时,它们连接在相同的电源线上,分别形成一个平行的分支电路。
根据并联规律,并联电阻的总电阻等于各个电阻的倒数之和的倒数,即1/Rt = 1/R1 + 1/R2 + 1/R3 + ...。
而并联电路中的电压保持不变,即各个电阻上的电压相等。
这些定律和规律为电路分析、设计和故障排除提供了重要的基础,使我们能够更好地理解和计算电路中的电压、电流和电阻之间的关系。

串联并联电压电流电阻的关系在电路中,电阻是一个非常重要的元件,它通过阻碍电流的流动来控制电路中的电压和电流。
而串联和并联是电路中两种常见的连接方式。
在本文中,我们将探讨串联和并联电阻对电压和电流的影响以及它们之间的关系。
1. 串联电阻的关系当电阻器按照串联的方式连接在一起时,它们的电阻值会相加。
也就是说,总的电阻等于每个电阻器的电阻值之和。
这是因为在串联电路中,电流只能顺着路径流动,必须通过每个电阻器。
因此,总的电阻会增加,从而降低电路中的电流。
根据欧姆定律,电压等于电流乘以电阻,所以电压也会随之增加。
2. 并联电阻的关系与串联电阻不同,当电阻器按照并联的方式连接在一起时,它们的电阻值会相互减小。
也就是说,总的电阻等于每个电阻器的电阻值的倒数之和的倒数。
在并联电路中,电流可以分为不同的路径流动,只需通过其中之一。
这样,总的电阻会减小,从而增加电路中的电流。
同样根据欧姆定律,电压等于电流乘以电阻,所以电压也会随之减小。
3. 串联和并联的关系串联和并联电阻的关系可以通过公式来表示。
假设有两个电阻器R1和R2,串联的总电阻为RT,并联的总电阻为RP。
那么有以下关系:1/RT = 1/R1 + 1/R2 (并联公式)RT = R1 + R2 (串联公式)从公式可以看出,串联的总电阻大于每个电阻器的电阻值之和,而并联的总电阻小于每个电阻器的电阻值。
这也是为什么在并联电路中,电流会选择通过电阻值较小的路径,而在串联电路中,电流会被限制在整个电路中。
4. 电压和电流的关系在串联和并联电路中,电压和电流之间也存在着一定的关系。
在串联电路中,电流的大小相同,而电压会在不同的电阻器之间分配。
电压的分配是根据电阻器的电阻值来进行的,电阻值越大,电压分配越大。
在并联电路中,电压的大小相同,而电流会根据电阻器的电阻值来分配。
电阻值越大,电流分配越小。
总结起来,串联和并联电阻对电压和电流有着不同的影响。
在串联电路中,总的电阻和电压会增加,电流会减小。
电阻串联和并联的计算电阻是电路中常见的元件之一,用于控制电流的流动和电压的大小。
在电路中,电阻可以串联或并联连接,以满足不同的电路要求和应用场景。
我们来看电阻的串联连接。
串联连接是指将多个电阻依次连接起来,电流依次通过每个电阻,形成电流的连续路径。
在串联连接中,电阻的总阻值等于各个电阻阻值之和。
假设有两个电阻R1和R2串联连接在一起,其总电阻记为RT,那么有如下关系式:RT = R1 + R2。
以一个简单的例子来说明串联连接的计算方法。
假设有两个电阻,一个阻值为10欧姆,另一个阻值为20欧姆,它们串联连接在一起。
根据串联连接的定义,总电阻等于两个电阻阻值之和,即RT = 10 + 20 = 30欧姆。
因此,串联连接后的电阻为30欧姆。
接下来,我们来看电阻的并联连接。
并联连接是指将多个电阻同时连接在电路中,形成电流分流的路径。
在并联连接中,电阻的总阻值等于各个电阻阻值的倒数之和再取倒数。
假设有两个电阻R1和R2并联连接在一起,其总电阻记为RT,那么有如下关系式:1/RT = 1/R1 + 1/R2。
同样以一个简单的例子来说明并联连接的计算方法。
假设有两个电阻,一个阻值为10欧姆,另一个阻值为20欧姆,它们并联连接在一起。
根据并联连接的定义,总电阻等于两个电阻阻值的倒数之和再取倒数,即1/RT = 1/10 + 1/20 = 3/20。
将等式两边取倒数,得到RT = 20/3 = 6.67欧姆。
因此,并联连接后的电阻为6.67欧姆。
在实际应用中,串联和并联连接常常被用于电路设计和电路分析中。
串联连接可以增加电路的总阻值,降低电流的流动,起到限流的作用。
而并联连接可以降低电路的总阻值,增大电流的流动,起到增流的作用。
这些特性使得串联和并联连接在电路中有着不同的应用。
总结起来,电阻的串联和并联连接是电路中常见的连接方式。
串联连接的总电阻等于各个电阻阻值之和,而并联连接的总电阻等于各个电阻阻值的倒数之和再取倒数。
电阻、电容和电感的串联与并联
两电阻R和R串联及并联时的关系:
两电容C和C2串联与并联时的关系:
串联
无互感的线圈的串联与并联:
两线圈串联: 两线圈并联:L= L 1L 2/ (L i + L 2)
有互感的线圈的串联与并联:
有互感两线圈顺串(异名端相接):L (顺)=L i + L 2+2M
L= L i + L 2
14
有互感两线圈并联: (2M 项前的符号:
同名端接在同一侧时取 接在同一侧时取+。
) (L i L 2-M 2
)仝 0,
W J LU
M
(最大)=札丄 2
互感的耦合系数:K= M /JLU
电桥
直流电桥由 A C 端接电源, 上下两臂平衡时, 数为0。
电桥平衡的条件:R/R 3= R 2/R N (或RR= R 2R 3) R 、R 2、和F 3为阻值已知标准电阻,被测电阻 R N = RR / R 1
有互感两线圈反串 L (顺)-L
(同名端相接):L (反)
=4M, M= [L (顺)
=L i + L 2 -2M
-L (反)]
L (并) = (L i L 2-M 2) / (L i + L 2 匚 2M
4个电阻首尾相接构成菱形,共4端,
B 、D 端之间为零位检测(检流计)。
B 、D 端电压差为零,检流计电流读
c 电桥原理图。
电路中的串联与并联电阻电路是由电阻、电源和导线等元件组成的物理系统,它能够将电能传输到各个部件上。
在电路中,串联与并联是两种常见的连接方式,用来连接电阻。
本文将详细介绍串联与并联电阻的概念、特性以及在电路中的应用。
1. 串联电阻串联电阻是指将多个电阻依次连接在同一电路中,其连接方式为正极与负极相连。
图示如下:(图示:串联电阻示意图)串联电阻的特点是电流在各个电阻之间保持相等,而总电阻等于电阻之和。
具体计算公式为:总电阻(Rt)= R1 + R2 + R3 + ... + Rn其中,R1、R2、R3等分别代表各个串联电阻的阻值。
串联电阻的应用广泛。
例如,当我们需要控制一组灯泡的亮度时,可以将各个灯泡串联连接,通过改变总电阻的阻值来调节亮度。
2. 并联电阻并联电阻是指将多个电阻连接在电路中,其连接方式为正极与正极相连、负极与负极相连。
图示如下:(图示:并联电阻示意图)并联电阻的特点是各个电阻之间的电压相等,而总电阻等于各个电阻的倒数之和的倒数。
具体计算公式为:总电阻(Rt)= (1/R1 + 1/R2 + 1/R3 + ... + 1/Rn)^(-1)其中,R1、R2、R3等分别代表各个并联电阻的阻值。
并联电阻也有多种应用场景。
例如,在家庭中,我们在使用电脑时需要连接电源和显示器等设备,由于这些设备的功率不同,可以使用并联电阻来实现电流的分配与平衡。
3. 串并联电阻的综合应用在实际电路中,常常会出现串联与并联电阻混合连接的情况。
在这种情况下,我们可以先按照串联与并联电阻的特性进行简化,然后再计算总电阻。
具体步骤如下:(1)先将一对一对的串联电阻进行简化,得到简化后的电阻值;(2)再将简化后的电阻与其他未简化的电阻进行并联,得到最终的总电阻。
通过这种串并联电阻的综合应用,可以减少电路的复杂度,简化计算过程。
总结:串联电阻与并联电阻在电路中起着重要的作用。
串联电阻保持电流相等,总电阻等于各个电阻之和;并联电阻保持电压相等,总电阻等于各个电阻的倒数之和的倒数。
电阻的串联与并联关系
电阻在电路中起到控制电流的作用,而电阻的串联与并联则是对多个电阻进行连接的方式。
了解电阻的串联与并联关系对于电路设计与分析非常重要。
一、电阻的串联连接
电阻的串联连接是指将多个电阻按照一定顺序连接起来,电流依次通过每个电阻。
串联连接时,多个电阻之间没有分支,形成了一个电阻的总和。
以两个电阻R1和R2的串联连接为例,其电路图如下所示:
```
—————[R1]—————[R2]—————
```
在串联连接的电路中,总电阻等于各个电阻之和:
R = R1 + R2
总电阻的增加使得电流减小,因为电流与电阻成反比。
二、电阻的并联连接
电阻的并联连接是指将多个电阻同时连接在电路中,各个电阻之间具有相同的电压。
并联连接时,多个电阻通过并联节点共享电流。
以两个电阻R1和R2的并联连接为例,其电路图如下所示:
```
—————[R1]—————
|
—————[R2]—————
```
在并联连接的电路中,总电阻满足以下计算公式:
1/R = 1/R1 + 1/R2
总电阻的计算是通过倒数求和得到的。
总电阻的减小使得电流增加,因为电流与电阻成正比。
三、串联与并联关系的实际应用
串联与并联连接在电路设计和应用中都有各自的优势和应用场景。
1. 串联连接的应用:
- 串联连接可以进行电阻值的叠加,可以实现灵活的电阻调节。
- 在电路中需要分配不同电压给各个电阻时,可以采用串联连接的方式。
- 串联连接可以降低电流,适用于需要控制电流大小的场合。
2. 并联连接的应用:
- 并联连接能够分摊电流,适用于需要大电流供应的场合。
- 并联连接可以降低总电阻,提高电路的效率。
- 在需要使各个电阻获得相同电压的情况下,可以采用并联连接。
除了串联与并联之外,电阻还可能存在一些特殊的连接方式,如星
型连接和三角形连接。
在实际电路设计中,根据不同的需求选择合适
的连接方式可以充分发挥电阻的作用。
总结:
电阻的串联与并联关系对电路的设计和分析有重要影响。
串联连接
使得电阻值叠加,电流依次通过各个电阻;并联连接能够分摊电流,
降低总电阻。
在实际应用中,需要根据具体需求选择合适的连接方式,以实现电流与电阻的控制和分配。
通过深入理解电阻的串联与并联关系,可以更好地理解电路工作原理,并进行电路设计与分析。