13分类数图形

（进士）春季备课教员：×××第三讲分类数图形一、教学目标：1、学会分类数图形的方法。

2、遵循不重复、不遗漏的原则，就能使数数的结果准确。

3、根据数的过程发现规律，培养有序思考问题的能力。

二、教学重点：学会分类数图形的方法。

遵循不重复、不遗漏的原则，就能使数数的结果准确。

三、教学难点：能够根据数的过程发现规律。

四、教学准备：PPT五、教学过程：第一课时（50分钟）一、导入（8分)师：同学们，你们看老师手上拿的是什么？生：扑克牌。

师：老师今天要用这其中的十张牌来玩一个游戏，想玩吗？生：非常想。

师：看，这里的A代表1，另外的是2到10。

大家都认识吗？生：认识。

师：那我们就来玩一下“我抽你猜”的游戏。

也就是老师任意从这十张牌中抽一张，你们来说我抽的是几，好吗？生：好。

（游戏开始，开始按一定的顺序抽，然后故意打乱顺序，也可以重复地抽相同的牌。

）师：同学们，太厉害了，这些牌都认识了。

现在老师要考考大家，谁能说说老师刚才抽牌的顺序？第一张抽的是几？第二张抽的是几？……生：（学生试着说。

）师：同学们都觉得说出来会比较吃力，并且很容易出错，是吗？生：是的。

师：老师也记不住，因为抽的牌太多了，太乱了是吗？生：是的。

师：现在我们重新玩一次，准备好了吗？（游戏开始，按从左往右的顺序抽，1-10的顺序。

）师：现在谁能告诉老师刚才的抽牌顺序？生：1-10。

师：太棒了！为什么两次都是玩抽牌游戏，第二次比第一次的顺序好记呢？生：因为老师第二次是按1-10的顺序来抽牌的。

师：对，我们按照一定的顺序来抽牌，就不会重复，也不会遗漏，并且能准确地记住刚才抽牌的顺序，是吧？生：是的。

师：那我们在数图形的时候，也要做到有序，这样才会做到不重复，不遗漏。

所以我们要学习分类数图形。

（板书课题：分类数图形）二、探索发现授课（37分）（一）例题一：（13分）右图中共有多少个三角形？师：同学们，以前做过这样的数图形题目吗？生：做过。

方法技巧练——运用分类法数图形的个数
1.在下图中找出平行四边形和梯形。

每种图形各有几个?
有6个平行四边形、8个梯形。

想:数图形的个数时,要按照一定的顺序分类列举,才能做到不重复、不遗漏。

分析:
2.下图中有几个平行四边形?几个梯形?
平行四边形有5个,梯形有9个。

【提示】用分类法数图形。

根据平行四边形的一条边所在位置找:①边是GF的有:平行四边形GFED,平行四边形GFDC;②边是HG的有:平行四边形ABGH,平行四边形BCGH;③边是HF的有:平行四边形BDFH。

根据梯形上底所在位置找:①上底是GF的梯形有:梯形GFEC,梯形GFEB,梯形GFDB;②上底是HG的梯形有:梯形ACGH,梯形ADGH,梯形BDGH;③上底是HF的梯形有:梯形AEFH,梯形BEFH,梯形ADFH。

3.下面的图形中,有几个平行四边形?有几个梯形?。

巧数图形巧数图形数图形包括：数线段、数角、数长方形、数正方形、数三角形等，这看似简单，其实其中学问可大了．为了能准确地数出结果，我们必须有次序、有条理地数，既不能遗漏，也不能重复．只要我们掌握了数的方法，就能数得又对又快．例1．下图中有多少条线段？（1）思路分析：每条线段均有两个端点，可以根据左端点进行分类．以A为左端点的线段为AB、AC，共有2条；以B点为左端点的线段为BC，只有1条；以C点为左端点的线段不存在．因此共有2＋1＝3(条)．答：图中共有3条线段．(2)这题中左端点是A的线段有：AB、AC、AD、AE，共有4条；左端点是B的线段有BC、BD、BE，共有3条；左端点是C的线段有C D、CE，共有2条；左端点是D的线段有DE；左端点是E的线段不存在．所以共有4＋3＋2＋1＝10(条)．答：图中共有10条线段．例2．数出下面图中共有多少条线段？思路分析：线段有一个重要特征：线段都是笔直的．所以我们在数的时候，必须将这幅图分成四个部分，每一部分分别采用以线段左端点分类数的方法，然后把四部分算得结果加起来．例题解答：第一部分从A到E共有4＋3＋2＋1＝10条线段．第二部分从G到J共有4＋3＋2＋1＝10条线段．第三部分是FG一条线段．第四部分是JK一条线段．10＋10＋1＋1＝22(条)答：这幅图共有22条线段．方法指导：数线段可以根据左端点将线段分类，数出每一类有多少条线段，然后再相加得出线段的总的条数．例3．一条线段上共有10个点，以这10个点为端点的不同线段共有多少条？思路分析：将这条线段上的10个点从左到右依次标为、、…、、以为左端点的线段为、、、、、、、、共有9条；为左端点的线段为、、、…、，共有8条；…；以为左端点的线段为，只有1条；以为左端点的线段不存在．因此，共有线段：9＋8＋…＋3＋2＋1＝(9＋1)×9÷2＝45(条)答：一共有45条线段．方法指导：一般地，如果线段上有几个点(其中n是大于或等于2的自然数)，那么以这n个点为端点的线段共有：(n－1)＋(n－2)＋…＋3＋2＋1＝n×(n－1)÷2例4．下面图形中有几个角？思路分析：数角的个数为了不遗漏、不重复，也需要按一定的顺序去数，可以采用与数线段相同的方法．以OA为一边的角有：∠AOB、∠AOC、∠AOD，共3个；以OB为一边的角有：∠BOC、∠BOD，共2个．以OC为一边的角有：∠COD，只有1个．3＋2＋1＝6(个)答：图中共有6个角．例5．数出下面图中共有多少个三角形？思路分析：数三角形个数的方法与数线段的方法差不多．以AB为边的三角形有：△ABD、△ABE、△ABC，共有3个．以AD为边的三角形有：△ADE、△ADC，共有2个．以AE为边的三角形有：△AEC，只有1个．所以，图中一共有三角形：3＋2＋1＝6(个)．我们还可以发现，可以抓住底边BC来考虑，底边BC中所包含的每一条线段都恰好对应一个三角形．底边左端点是B的三角形共有△BDA、△BEA、△BCA三个．底边左端点是D的三角形共有△DEA、△DCA两个．底边左端点是E的三角形只有△ECA一个．所以一共有三角形：3＋2＋1＝6(个)．方法指导：数角的个数和三角形个数这些基本图形时，所采用的方法与数线段的方法相同．即角的个数＝射线数×(射线数－1)÷2．即三角形个数就是底边上的线段数．例6．数一数图中共有多少个三角形？思路分析：我们可以将这幅图分成三个部分来数，即下面三幅图．在△ABC中，一共有5＋4＋3＋2＋1＝15(个)三角形，在△ABD中，一共有5＋4＋3＋2＋1＝15(个)三角形；在△BDC中，一共有5个三角形．15＋15＋5＝35(个)答：图中共有35个三角形．例7．图中共有多少个不同的三角形？思路分析：将本题分成(1)、(2)两部分来数：第(1)部分中共有三角形：3＋2＋1＝6(个)；第(2)部分中共有3＋2＋1＝6(个)三角形．所以，共有三角形6＋6＝12(个)．例8．数出下图中共有多少个三角形？思路分析：这题我们可以采用按基本图形组合的方法来数．把图中最小的一个三角形看作基本图形．由一个基本三角形构成的三角形共有8个；由两个基本三角形构成的三角形共有4个；由四个基本三角形构成的三角形共有4个．因此：8＋4＋4＝16(个)，所以，图中共有16个三角形．例9．数出下面图形中共有多少个三角形？思路分析：这题采用把其中最小的三角形作为一个基本图形，然后分类相加的方法．由一个基本三角形构成的三角形共有9个；由四个基本三角形构成的三角形共有3个；由九个基本三角形构成的三角形只有1个．因此9＋3＋1＝13(个)，所以，图形中共有13个三角形．例10．下面两幅图中各有多少个长方形？思路分析：(1)中长方形都是竖向的，可以利用对应的方法来数．因为每个长方形都和底边上的一条线段对应，因此用数长边上的线段条数来数长方形的个数．所以，图中长方形共有4＋3＋2＋1＝10(个)．(2)我们可用按基本图形组合的方法来数．由一个基本长方形构成的长方形共有6个；由两个基本长方形构成的长方形共有7个；由三个基本长方形构成的长方形共有2个；由四个基本长方形构成的长方形共有2个；由六个基本长方形构成的长方形有1个；所以，图中共有长方形6＋7＋2＋2＋1＝18(个)．本题还可以结合数线段的方法，这题中长方形的长被分成了3段，线段总数为3＋2＋1＝6条，宽被分成了2段，线段总数为2＋1＝3 (条)．由此可见，长方形的个数＝6×3＝18(个)．于是，可以整理出数长方形个数的方法：长方形的个数等于原长方形长上的线段数乘以宽上的线段数．例11．数出各图中正方形的个数．思路分析：(1)中最基本的正方形有9个，即边长为1的正方形有9个(9＝3×3)；由4个基本正方形组成的正方形，即边长为2的正方形有4个(4＝2×2)；由9个基本正方形组成的正方形，即边长为3的正方形有1个(1＝1×1)所以共有正方形9＋4＋1＝14(个)．(2)中边长为1的正方形有16个，即16＝4×4；边长为2的正方形有9个，即9＝3×3；边长为3的正方形有4个，即4＝2×2；边长为4的正方形有1个，即1＝1×1．所以共有正方形有16＋9＋4＋1＝30(个)．因此，如果一个正方形的各边被分成几个等份，那么正方形的个数便是1×1＋2×2＋3×3＋…＋n×n．方法指导：正确数出图形的个数，首先要弄清图形中包含的基本图形是什么，有多少个．然后再从各图形中所包含基本图形的个数多少出发，依次数出它们的个数，并求出它们的和是多少．有些图形被分成了几个部分，可以先从各部分的基本图形出发，数出所含图形的个数，再求各部分的总和．例12．图中共有多少个正方形？思路分析：将正方形分类，将每一类的总数相加，就可得到所有正方形的个数．由两块小三角形构成的正方形有4个；由四块小三角形构成的正方形有4个；由八块小三角形构成的正方形有1个；由十六块小三角形构成的正方形有1个．由一、三、五、七、六、九、十、十一、十二、十三、十四、十五块小三角形不能构成正方形．所以，图中共有4＋4＋1＋1＝10(个)正方形．例13．数出图中共有多少个正方形？思路分析：根据正方形边长的大小，我们将它们分成四类：第1类：边长为1的正方形有24个；第2类：边长为2的正方形有13个；第3类：边长为3的正方形有4个；第4类：边长为4的正方形有1个．所以图中共有24＋13＋4＋1＝42(个)正方形．这题如果把四条边长多出的8个小正方形去掉，很容易得出共有1×1＋2×2＋3×3＋4×4＝30(个)正方形，添上了去掉的小正方形后，这8个小正方形还能再和其他图形组成4个新的正方形．所以，图中共有30＋8＋4＝42(个)正方形．例14．下图中共有多少个长方形？思路分析：我们可以先将大长方形中的5小块编上号：这5块都是符合要求的长方形．然后数由两小块拼成的长方形，共有4个，即①＋②，②＋③，③＋④，④＋⑤；再数由三小块拼成的长方形，共有2个，即①＋③＋④，③＋④＋⑤；没有由四小块拼成的长方形；最后数由5小块拼成的长方形只有最大的一个．所以，图中共有5＋4＋2＋1＝12(个)长方形．例15．数出下图中共有多少个三角形？思路分析：首先将大三角形中六小块分别编上号．通过观察，我们可以发现这6小块中，④和⑤不是三角形，因此，由一块形成的三角形有4个；由两块拼成的三角形有5个，即分别是①＋②，①＋③，③＋④，②＋④，⑤＋⑥；由三块拼成的三角形有两个，分别为①＋③＋⑤，②＋④＋⑥；由四块拼成的三角形有1个，即是①＋②＋③＋④；没有由五块拼成的三角形；由六块拼成的三角形有1个，即最大的三角形．所以，图中三角形一共有4＋5＋2＋1＋1＝13(个)．方法指导：数长方形、正方形、三角形以及一些不规则的图形都可以采用编号数图形的方法，就是将原来图中的每一小块都编上号，先看每一小块是否符合要求的图形，接着数由两个小块相拼成的图形中有几个是符合要求的图形，再依次数由三小块、四小块……拼成的图形中各有几个是符合要求的图形，最后将每一步数得的结果加起来．。

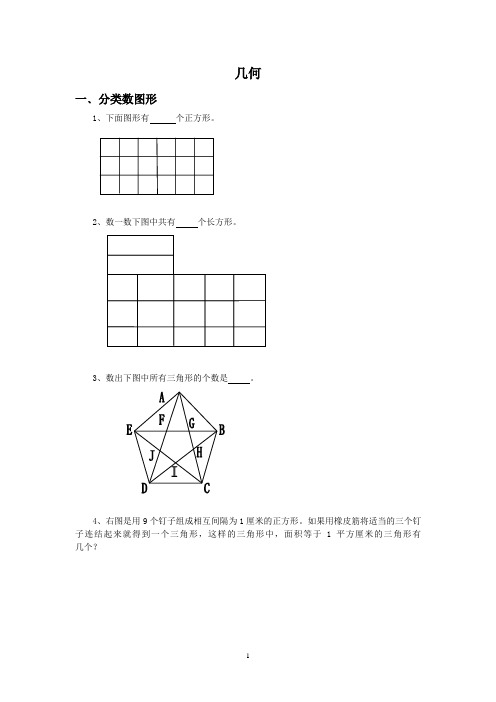
几何一﹑分类数图形1、下面图形有个正方形。

2、数一数下图中共有个长方形。

3、数出下图中所有三角形的个数是。

4、右图是用9个钉子组成相互间隔为1厘米的正方形。

如果用橡皮筋将适当的三个钉子连结起来就得到一个三角形，这样的三角形中，面积等于1平方厘米的三角形有几个？5、数一数下图中，左图共有 个三角形，共有 条线段；右图共有 个三角形，共有 条线段。

6、下图中中各共有 个正方形.7、下图中中共有 个长方形.8、下图中共有 个梯形.9、下图中共有个三角形.10、下图中有个正方形.11、下图中有个三角形.12、下图中有个三角形.13、下图中共有个正方形.14、下图中有个长方形.15、下图中共有个梯形.16、下图中共有个长方形。

所有这些长方形面积的和是 .（单位：厘米）17﹑数一数下图中，左图共有个平行四边形，右图共有个平行四边形。

18、求下图中各线段长度的总和。

（单位：厘米）19、一把直尺，大部分刻度已经看不清楚，能看清楚的刻度有5个（如下图），用这把尺能直接量出多少个不同的长度？20、下面图中共有个三角形21、图中共有个三角形22、下图中共有个三角形23、图中共有个正方形24、图中共有梯形25、数一数，图中共有个三角形26、9人参加会议，如果每人都要和参加会议的人都握一次手。

问参加会议的人一共要握多少次手？27、宴会结束时总共握手28次，如果参加宴会的每一个人，和其他每一个人都握一次手。

问参加宴会一共有多少人？28、乒乓球男子团体比赛，共有15个队参加循环赛，按积分决出冠军，共需比赛多少场？29、一条线段上，除两端共有49个点，一共有多少条线段？30﹑从成都到南京的某次快车，中途要停靠9个大站。

铁路局要为这次快车准备多少种不同的车票？这些车票中有多少种不同的票价？二﹑面积I1、有一长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？2、街心花园中一个正方形的花坛四周有1米宽的水泥路。

教案：《数图形的学问》四年级上册数学北师大版一、教学目标1. 让学生通过观察、操作、交流等活动，认识和理解图形的分类和特征，培养空间观念。

2. 培养学生运用数形结合的方法解决问题的能力，提高学生的数学思维能力。

3. 培养学生合作、探究的学习习惯，增强学生的团队意识和沟通能力。

二、教学内容1. 图形的分类和特征2. 数图形的方法3. 解决实际问题三、教学重点与难点1. 教学重点：图形的分类和特征，数图形的方法。

2. 教学难点：解决实际问题，运用数形结合的方法。

四、教学准备1. 教学课件2. 图形卡片3. 学生分组，每组准备一张大白纸、彩笔等。

五、教学过程1. 导入新课（5分钟）利用课件展示一组图形，引导学生观察并说出它们的名称。

让学生思考：这些图形有什么共同点？如何对它们进行分类？2. 图形的分类和特征（10分钟）1. 教师引导学生通过观察、操作，发现图形的分类方法。

2. 学生分组讨论，总结各类图形的特征。

3. 各组汇报讨论成果，师生共同总结。

3. 数图形的方法（10分钟）1. 教师介绍数图形的方法，如点数法、线数法、面积法等。

2. 学生分组讨论，探讨如何运用这些方法解决实际问题。

3. 各组汇报讨论成果，师生共同总结。

4. 解决实际问题（10分钟）1. 教师出示一道实际问题，引导学生运用数形结合的方法解决问题。

2. 学生分组讨论，共同解决问题。

3. 各组汇报讨论成果，师生共同总结。

5. 课堂小结（5分钟）教师引导学生回顾本节课所学内容，总结图形的分类和特征，以及数图形的方法。

六、课后作业1. 完成课本相关练习题。

2. 收集生活中的图形，进行分类和数图形的练习。

七、板书设计1. 图形的分类和特征2. 数图形的方法3. 解决实际问题八、教学反思本节课通过观察、操作、交流等活动，让学生认识和理解图形的分类和特征，培养学生运用数形结合的方法解决问题的能力。

在教学过程中，要注意关注学生的个体差异，给予每个学生充分的表达和思考空间。

小学数学《数图形》教案教学内容：教学目标：学会数图形的技巧和方法教学难点：把一些图形放在一起，如何既不遗漏，又不重复地数出来，还有一些复杂的图形由若干个基本图形组合而成教学过程一、快速抢答：（课件出示）1、把一只鸡和一只鹅同时放进冰箱里，为什么鸡死了鹅没有死？答案：企鹅嘛。

2、什么人生病从来不看医生？答案：盲人。

3、哪一年哪月有二十八天？答案：每个月都有二十八号。

4、用铁锤锤鸡蛋为什么锤不破？答案：铁锤当然不会破了。

5、冬瓜、黄瓜、西瓜、南瓜都能吃，什么瓜不能吃？答案：傻瓜。

二、复习旧知．三、探索新知：（一）教学例1．1、出示例1：数图形。

正方形( )个长方形（）个三角形（）个圆形（）个平行四边形（）个2、引导学生读题，分析题意：上图中图形摆放的比较凌乱，数这样的凌乱放置的图形，不同的图形用不同的标记做记号，如图：3、学生自主探究。

4、交流汇报，教师点拨。

解：正方形（2）个；长方形（4）个；三角形（3）个；圆形（4）个；平行四边形（1 ）个。

（二）巩固练习：看一看，下图中共有几种图形，并数出每种图形的个数。

正方形（）个；长方形（）个；三角形（）个；圆形（）个。

（三）教学例2．1、出示例题：数一数，图中共有多少条线段？2、引导学生读题，分析题意：一段一条的有4条；两段一条的有3条；三段一条的有2条；四段为一条的有1条。

解：一共有4+3+2+1=10（条）3、学生自主探究。

4、交流汇报，教师点拨。

（四）巩固练习：数一数，下图中有（）个角。

（五）教学例3．1、出示例3：下图中共有（）个。

2、引导学生读题，分析题意：这道题可以按照的大小来分类。

图中有4个小的，还有一个由4个组成的大。

如图：3、学生自主探究。

4、交流汇报，教师点拨。

解：共有（5）个。

（六）巩固练习：数图形。

（）个长方形（）个正方形（七）教学例4．1、出示例4：下图中共有（）三角形。

2、引导学生读题，分析题意：这道题可以按照三角形大小分类来数，图中共有4个大小不同的三角形。

第1讲组合图形的计数第一关【知识点】1．组合图形的概念：圆，三角形，正多边形，梯形，平行四边形为基本图形其余的为组合图形，可以用辅助线分解为基本图．2．组合图形的计数实质上就是分类数图形，解决方法是：（1）合理进行分类．（2）利用排列组合的有关公式进行每一个类的数量计算．（3）将所有的类的数量进行相加．（4）仔细检查，防止遗漏．【例1】图中有多少个三角形？【答案】3【例2】数一数，图中一共有多少个三角形？【答案】13【例3】数一数，图中一共有多少个三角形？【答案】27【例4】数一数，图中一共有多少个三角形？【答案】48【例5】数一数，图中一共有多少个三角形？【答案】9【例6】数一数，图中一共有多少个三角形？【答案】8【例7】数一数，图中一共有多少个三角形？【答案】8【例8】数一数，图中一共有多少个三角形？【答案】20；24；24【例9】数一数，图中一共有多少个三角形？【答案】35【例10】数一数，图中一共有多少个三角形？【答案】67【例11】数一数，图中一共有多少个三角形？【答案】11【例12】数一数，图中一共有多少个三角形？【答案】40【例13】图中，有多少个三角形？【答案】16【例14】数一数，图中一共有多少个三角形？【答案】8【例15】数一数，图中一共有多少个三角形？【答案】13【例16】数一数，图中一共有多少个三角形？【答案】12【例17】数一数，图中一共有多少个三角形？【答案】11【例18】数一数，图中一共有多少个三角形？【答案】20【例19】数一数，图中一共有多少个三角形？【答案】12【例20】如图中有多少个三角形？【答案】27【例21】如图中有多少个三角形？【答案】17【例22】如图中有多少个三角形？【答案】10【例23】数一数，图中有多少个三角形？【答案】27【例24】图中有多少个三角形？【答案】14【例25】图中有多少个三角形？【答案】11【例26】数一数，图中共有多少个三角形？【答案】15【例27】如图是一些等腰直角三角形组成的图形，图中一共有多少个三角形？【答案】23【例28】如图中，一共有多少个三角板？【答案】12【例29】如图中共能数出多少个三角形？【答案】24【例30】如图中共能数出多少个三角形？【答案】24【例31】在△ABC中，D1、D2、D3为AB边的内分点，E1、E2、E3为AC边的内分点，那么图中有　多少个三角形？【答案】64【例32】如图中共能数出多少个三角形？【答案】11【例33】如图中，共有多少个三角形？【答案】10【例34】数一数，图中共有多少个三角形？【答案】10【例35】数一数，图中共有多少个三角形？【答案】12【例36】数一数，图中共有多少个三角形？【答案】16【例37】数一数，图中共有多少个三角形？【答案】18【例38】数一数，图中共有多少个三角形？【答案】30【例39】数一数，图中共有多少个三角形？【答案】28【例40】如图中，一共有多少个三角形？【答案】32【例41】如图中，一共有多少个三角形？【答案】72【例42】如图中，一共有多少个三角形？【答案】22【例43】图中共有多少个三角形？【答案】60【例44】下图中共有多少个三角形？【答案】8【例45】下图中共有多少个三角形？【答案】24【例46】下图中共有多少个三角形？【答案】34【例47】下图中共有多少个三角形？【答案】35【例48】下图中共有多少个三角形？【答案】16【例49】下图中共有多少个三角形？【答案】30【例50】下图中共有多少个三角形？【答案】22【例51】下图中共有多少个三角形？【答案】62【例52】下图中共有多少个三角形？【答案】10【例53】下图中共有多少个三角形？【答案】35【例54】下图中共有多少个三角形？【答案】32【例55】下图“七角星”中共有多少个三角形？【答案】35【例56】下图中共有多少个三角形？【答案】20【例57】下图中共有多少个三角形？【答案】40【例58】如图，图中3个大三角形都是等边三角形，则图中共有多少个三角形？【答案】30【例59】如图中有多少个三角形？【答案】76【例60】如图中有多少个三角形？【答案】76【例61】如图中，包含“”的三角形有多少个？【答案】4【例62】如图，数一数其中共有多少个包含“☆”的三角形？【答案】8【例63】如图是由18个大小相同的小正三角形拼成的四边形．其中某些相邻的小正三角形可以拼成较大的正三角形若干个．那么，图中包含“*”号的大、小正三角形一共有多少个？【答案】6【例64】如图，图中包含“★”的大、小三角形共有多少个？【答案】12【例65】数一数如图中共有多少个包含“﹡”号的三角形？【答案】6【例66】图中，共有多少个直角三角形？【答案】16【例67】图中，共有多少个等边三角形？【答案】14【例68】数一数，图中一共有多少个正三角形？【答案】44【例69】如图，四边形ABCD与CEFG是边长相等的正方形，且B、C、G在一条直线上，则图中有多少个等腰直角三角形？【答案】22【例70】如图，连接一个正六边形的各顶点，问图中共有多少个等腰三角形（包括等边三角形）？【答案】38【例71】圆周上有8个点，把它们两两相连，若任意三条线都不交于一点，那么图中顶点全在圆内的三角形共有多少个？【答案】56【例72】如图，有这样的两条线，请问从这5个点中任选三个点可以构成多少个不同的三角形？【答案】8【例73】木板上钉有五颗钉子（如图所示，排成两行），用橡皮筋可以套出多少个三角形？【答案】9【例74】如图，木板上有10根钉子，任意相邻的两根钉子距离都相等，以这些钉子为顶点，用橡皮筋可套出多少个正三角形?【答案】13【例75】以平面上4个点为端点连接线段，形成的图形中最多可以有多少个三角形？【答案】8【例76】平面上有四个点，任意三个点都不在﹣条直线上．以这四个点为端点连接六条线段，在所组成的图形中用它们作顶点可以组成多少个三角形？【答案】4【例77】以平面上任意4个点为顶点的三角形中，钝角三角形最多有多少个？【答案】4【例78】从图中两个正方形的7个顶点中选出3个点作为顶点构成三角形，一共可以构成多少个不同的三角形？【答案】32【例79】如图由5个大小相同的正方形构成．以图中12个点为顶点的三角形共有多少个？【答案】200【例80】长方形内有2017个点，连同长方形的4个顶点在内，共有2021个点，任意3个点都不在同一条直线上，以这2021个点中的某三点为顶点，可作出多少个互不重叠的三角形?【答案】4036【例81】如图，是由9个点组成的点阵，那么以图中3个点为顶点的直角三角形有多少个？【答案】44【例82】如图有12个点，相邻两个点之间的距离是1厘米，这些点为顶点可以连成多少个面积为3平方厘米的三角形？【答案】26【例83】如图是由四个边长为1的小正方形组织的图形，图中共有9个格点（格点即为小正方形的顶点）．如果以这些格点为顶点，那么一共可组成多少个等腰三角形?【答案】36【例84】如图是由32个面积为1的等边三角形组成的一个大的平行四边形，这个大的平行四边形内部及边上共有25个交叉点．以这些交叉点为顶点，可以连成多少个等边三角形？【答案】28【例85】在一个圆周上均匀分布10个点，以这些点为顶点，可以画出多少个不同的钝角三角形？（补充知识：由直径和圆周上的一点构成的三角形一定是直角三角形，其中直径的边所对的角是直角，所以如果圆周上三点在同一段半圆周上，则这三点构成钝角三角形）【答案】60【例86】用9个钉子钉成相互间隔为l厘米的正方阵（如图）．如果用一根橡皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于1平方厘米的三角形有多少个？【答案】32【例87】如图由4个正六边形组成，每个面积是6，以这4个正六边形的顶点为顶点，可以连接面积为4的等边三角形有多少个？【答案】8【例88】如图，大三角形由9个形状、大小相同的等边三角形组成，共有10个顶点，以这些顶点为顶点构成的三角形中，面积与阴影部分面积相等的三角形共有多少个?【答案】36【例89】如图，一小正方形的边为边向小正方形外作四个正方形，再依次连接几个定点，若图中阴影三角形的面积是S，则面积为2S的三角形有_______个，面积为8S的正方形有_______个【答案】20；1【例90】如图由九个边长为1厘米的正方形组成，在如图中面积为0.5平方厘米的三角形有_______个．面积为1平方厘米的三角形有_______个，面积为1.5平方厘米的三角形有_______个，面积最大的三角形的面积是_______平方厘米．【答案】5；11；2；2.5【例91】在图中填上2条直线，最多能数出多少个三角形？【答案】10【例92】今有甲、乙两个大小相同的正三角形，各画出了一条两边中点的连线，如图，甲、乙位置左右对称，但甲、乙内部所画线段的位置不对称，从图中所示的位置开始，甲向右水平移动，直至两个三角形重叠后在离开．在移动过程中的每个位置，甲与乙所组成的图形中都有若干个三角形，那么三角形个数最多的位置，图形中有多少个三角形？【答案】11【例93】如图，在正方形的内部放入1个点，就可以把原来的正方形分成了4个小三角形；在正方形的内部放入2个点，就可以把原来的正方形分成了6个小三角形．那么如果在正方形的内部放入10个点，最多能把原来的正方形分成了多少个小三角形?【答案】22【例94】在一张三角形纸内任作2009个互不重合的点（所有的点都不在三角形的任意一条边上），以这2009个点和三角形纸的3个顶点为顶点的三角形，最多能剪出多少个？【答案】4019【例95】在三角形ABC中，D是BC的中点，图中面积相等的三角形共有多少对？【答案】6第二关【知识点】【例96】图中一共能数出多少正方形？【答案】26【例97】图中一共能数出多少正方形？【答案】55【例98】图中一共能数出多少正方形？【答案】26【例99】图中一共能数出多少正方形？【答案】23【例100】图中一共能数出多少正方形？【答案】14【例101】．将4×4的大正方形切割为16个1×1的小正方形，擦去其中的两条线段，得到如图所示图形．则图中一共有多少个正方形？【答案】22【例102】图中一共能数出多少正方形？【答案】20【例103】图中一共能数出多少正方形？【答案】13【例104】图中一共能数出多少正方形？【答案】17【例105】图中一共能数出多少正方形？【答案】35【例106】图中一共能数出多少正方形？【答案】46【例107】图中一共能数出多少正方形？【答案】10【例108】图中一共能数出多少正方形？【答案】14【例109】图中共有多少个正方形？【答案】17【例110】数一数，图中共有多少个正方形？【答案】23【例111】数一数，图中共有多少个正方形？【答案】18【例112】数一数，图中共有多少个正方形？【答案】11【例113】数一数，图中共有多少个正方形？【答案】20【例114】数一数，图中共有多少个正方形？【答案】15【例115】数一数，图中共有多少个正方形？【答案】28【例116】如图由相同的正方形和相同的等腰直角三角形构成，求正方形的个数。

奥数一、数图形数线段方法1、打枪法：朝一个方向打，按照一定顺序打。

方法2、基本线段法【定义】直线上的端点数比基本线段数大1 。

问题一、一直线有9 个端点，能组成几条线段？题解：一直线有9 个端点，此直线上的基本线段数为8，所能组成的线段数为：8+7+6+5+4+3+2+1＝36（条）。

数图形【定义】基本图形法（基本图形：在图中最小的图形，不能再被分割）【要点】数图形就要先数基本图形。

问题二、求图中含有三角形的个数解题：上图含有3 个基本三角形，图中含有三角形个数为：3+2+1＝6（个）。

【要点】数图形的角就先数基本角。

问题三、求图中含有几个锐角解题：上图最大角为锐角，基本角有4个，图中含有锐角数量为：4+3+2+1＝10（个）分类法：分层法、分边法【分层法】当图形不是我们前面学过的基本图形，但通过观察可以发现里面包含有基本图形，并且是可以通过分层的方法来得到基本图形时，我们就用分层数的方法。

如上图，三角形中加一条横线，分成上下2 层，上层是三角形，下层为梯形，上、下合起来为三角形；上层2 个基本三角形，图形数为2+1＝3（个）,下层无三角形，三角形数为0 ,上、下组合时，有2 个基本三角形，图形数为2+1＝3（个），此图形中三角形总数为：3+0+3＝6（个）。

【分边法】将图形分为左、右2边来数，左边有2个基本三角形，图形数为：2+1＝3（个），右边有2个基本三角形，图形数为：2+1＝3（个），左、右合并后的图形如右图，图中含有2个三角形，本题图中含有三角形的总数为：3+3+2＝8（个）图中恰含1个三角形的有6个，分别：①、②、③、④、⑤、⑥恰含2个三角形的有3 个，分别：①②、③④、⑤⑥恰含3个三角形的有6个，分别：①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②恰含4、5个三角形的均为：0，恰含6个三角形的有：1个；此图中含有三角形的个数为：6+3+6+1+1＝16（个）。