全等三角形(常见辅助线)

几何证明-常用辅助线(一)中线倍长法:例1 、求证：三角形一边上的中线小于其他两边和的一半。

已知：如图，△ABC 中，AD 是BC 边上的中线，求证：AD ﹤21(AB+AC) 分析：要证明AD ﹤21(AB+AC)，就是证明AB+AC>2AD ，也就是证明两条线段之和大于第三条线段，而我们只能用“三角形两边之和大于第三边”，但题中的三条线段共点，没有构成一个三角形，不能用三角形三边关系定理，因此应该进行转化。

待证结论AB+AC>2AD 中，出现了2AD ，即中线AD 应该加倍。

证明：延长AD 至E ，使DE=AD ，连CE ，则AE=2AD 。

在△ADB 和△EDC 中，AD =DE ∠ADB =∠EDC BD =DC∴△ADB ≌△EDC(SAS) ∴AB=CE又 在△ACE 中，AC+CE ＞AE∴AC+AB ＞2AD ，即AD ﹤21(AB+AC)小结：(1)涉及三角形中线问题时，常采用延长中线一倍的办法，即中线倍长法。

它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中，以利于问题的获解。

课题练习:ABC ∆中，AD 是BAC ∠的平分线，且BD=CD ，求证AB=AC 例2:中线一倍辅助线作法 △ABC 中方式 AD 是BC 边中线方式2：间接倍长作CF ⊥AD 于F ，延长MD 到N ， 作BE ⊥AD 使DN=MD ， 连接BE 连接CD 例3：△ABC 中，AB=5，AC=3，求中线例4：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE 课堂练习：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 交AC 于F ，求证：AF=EF例5：已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠C 第 1 题图A DBCE图2-1课堂练习：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE 作业：1、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

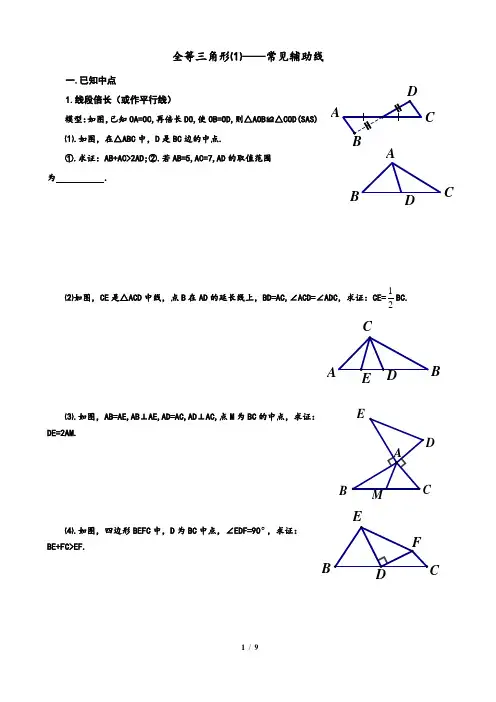
全等三角形⑴----常见辅助线一.已知中点1.线段倍长（或作平行线）模型：如图，已知OA=OC,再倍长DO,使OB=OD,则△AOB≌△COD(SAS)⑴.如图，在△ABC中，D是BC边的中点.①.求证：AB+AC>2AD;②.若AB=5,AC=7,AD的取值范围为 .⑵如图，CE是△ACD中线，点B在AD的延长线上，BD=AC,∠ACD=∠ADC，求证：CE=12BC.⑶.如图，AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点，求证：DE=2AM.⑷.如图，四边形BEFC中，D为BC中点，∠EDF=90 ，求证：BE+FC>EF.CBDBBA C2.作垂线(知中点作垂线；证中点作垂线)模型：如图，OA=OB,BC ⊥CD,AD⊥CD,则△AOD ≌△BOC(AAS) ⑴.如图，△ABC 中，D 为BC 的中点.①在图中作出CM ⊥AD,BN⊥AD,垂足分别为点M,N; ②⑵求证：DM=DN; ③若AD=3，求AM+AN 的值.⑵.如图，CD 为△ABC 的角平分线，E,F 分别在CD,BD 上，且DA=DF,EF=AC.求证：EF ∥BC.⑶.如图，BC ⊥CE,BC=CE,AC ⊥CD,AC=CD,DE 交AC 的延长线于点M,M 是DE 的中点. ①求证：AB ⊥AC;②若AB=8，求CM 的长.⑷.如图，已知A(-2,1),C(0,2),且C 为线段AB 的中点，求点B 的坐标.DABCABA3.证中点【方法技巧】证线段的中点，常过线段的端点构造一组平行线，或过线段的两端点向过中点的线段作垂线，根据AAS 或ASA 构造全等三角形，证题关键往往是证明一组对应边相等.【作平行证中点】⑴.如图，在△ABC 中，∠ABC=∠ACB，D,E 分别是AC 和AC 的延长线上的点，连接BD,BE,若AB=CE ，∠DBC=∠EBC.求证：D 是AC 的中点.⑵.如图，AB⊥AE,AB=AE,AC⊥AD,AC=AD,AH⊥DE 于点H,延长AH 交BC 于点M.求证：M 是BC 的中点.【作垂线证中点】⑶.如图，AB⊥AC,AB=AC,D 是AB 上一点，CE⊥CD,CE=CD,连接BE 交AC 于点F ，求证：F 是BE 的中点.⑷如图，A,B,C 三点共线，D,C,E 三点共线，∠A=∠DBC,EF⊥AC 于点F ，AE=BD. ①求证：C 是DE 的中点；②求证：AB=2CF.EBEB二、线段的和差处理 1.等线段代换法⑴如图，CD 为△ABC 的中线，M,N 分别为直线CD 上的点，且BM ∥AN. ①求证：AN=BM;②求证：CM+CN=2CD⑵如图，△ABC 中，∠BAC=90︒，AB=AC,AN 是过点A 的一条直线，且BM ⊥AN 于点M ，CN ⊥AN 于点N. ①求证：AM=CN ；②求证：MN=BM-CN.⑶如图，在△ABC 中，AD ⊥BC 于D ，且AD 平分∠BAC,CE ⊥AB 于点E ，交AD 于点F. ①求证：BD=CD;②若AF=BC,求证：AC-CE=EF.⑷.如图，△ABC 中，AC=BC,∠ACB=90︒，D 为BC 延长线上一点，BF ⊥AD 于点F ，交AC 于点E.①求证：BE=AD ；②过C 点作CM ∥AB 交AD 于点M ，连接EM ，求证：BE=AM+EM.ABACBA B2.截长补短法（直接和间接）如图，△ABC中，∠CAB=∠CBA=45 ，CA=CB,点E为BC的中点，CN⊥AE交AB于点N.①求证：∠1=∠2；②求证：AE=CN+EN. （用多种方法）方法1：直接截长方法2：间接载长方法3：直接补短方法4：间接补短EBCA EBCA EBCA EBC A三、角平分线模型1.作垂线模型：如图，∠1=∠2，PA⊥OA,PB⊥OB,则PA=PB.⑴如图，△ABC中，CD是角平分线，AC=3,BC=5,求S△ACD∶S△BCD的值.⑵.如图，四边形ABCD中，AC平分∠BAD，CE⊥AB于点E，且∠B+∠D=180︒，求证：AE=AD+BE.⑶.如图，△ABC中，AC>AB,F为BC的中点，FD⊥BC,交∠BAC的平分线于点D，DE⊥AC于点E.①求证：BD=CD;②求证：AB+AC=2AE;③直接写出-AC ABCE的值是 .⑷如图，△ABC中，AB=AC，D为△ABC外一点，且∠1=∠2，AB⊥BD于点M.①求证：AD平分△BDC的外角；②求-BD CDDM的值.21BAOPA BB CD2.截长补短模型：如图，若∠AOP=∠BOP,OA=OB，则△OAP≌△OBP⑴.如图，四边形ABCD中，AC平分∠DAB，∠B+∠D=180 ，求证：CD=CB.⑵.△ABC中，AB>AC,AD平分∠BAC，AE=AC，连DE.①求证：∠C>∠B;②若AB-AC=2,BC=3，求△BED的周长.⑶.如图，AD∥BC，E是CD上一点,且∠1=∠2，∠3=∠4，求证：AB=AD+BC⑷.如图，BC>AB,AD=CD，∠1=∠2，探究∠BAD与∠C之间的数量关系.(多种方法)C BBBBA3.角平分线+垂线：延长法模型：如图，若∠1=∠2，AC⊥OC，延长AC 交OB 于点B ，则△OCA≌△OCB. ⑴.如图，在△ABC 中，AD 平分∠BAC，CE⊥AD 于点E ，探究∠ACE，∠B，∠ECD 之间的数量关系.⑵.如图，在△ABC 中，AB<BC ，BP 平分∠ABC，AP⊥BP 于P 点，连接PC ，若△ABC 的面积为4，求△BPC 的面积.⑶.如图，在△AOB 中，AO=OB ，∠AOB=90 ，BD 平分∠ABO 交AO 于点D ，AE ⊥BD 交BD 的延长线于点E ，求证：BD=2AE.⑷.如图，四边形ABCD 中，AD∥BC，AE,BE 分别平分∠DAB,∠CBA.①求证：AE⊥BE；②求证：DE=CE ；③若AE=4,BE=6,求四边形ABCD 的面积.BBA B四、半角与倍角模型⑴如图，已知AB=AC,∠BAC=90°,∠MAN=45°,过点C作NC⊥AC交AN于点N,过点B作BM⊥AB交AM 于点M，连接MN.①当∠MAN在∠BAC内部时，求证：BM+CN=MN.②如图，在①的条件下，当AM和AN在AB⑵如图，在△ABC中，CA=CB,∠ACB=120°,E为AB上一点，∠DCE=60°,∠DAE=120°,求证：DE-AD=BE.⑶如图，在△ABC中，CA=CB,∠ACB=120°,点E为AB上一点，∠DCE=∠DAE=60°,求证：AD+DE=BE.⑷.①如图1，在四边形ABCD中，AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点，且∠EAF=1 2∠BAD,求证：EF=BE+DF;②如图2，在①条件下，若将△AEF绕点A逆时针旋转，当点E,F分别运动到BC,CD延长线上时，则EF,BE,DF之间的数量关系是 .BN MDB A BC。

全等三角形问题中常见的辅助线的作法总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用D C BAED F CB A的思维模式是全等变换中的“旋转”法构造全等三角形．3)遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

（3）可以在该角的两边上，距离角的顶点相等长度的位置上截取二点，然后从这两点再向角平分线上的某点作边线，构造一对全等三角形。

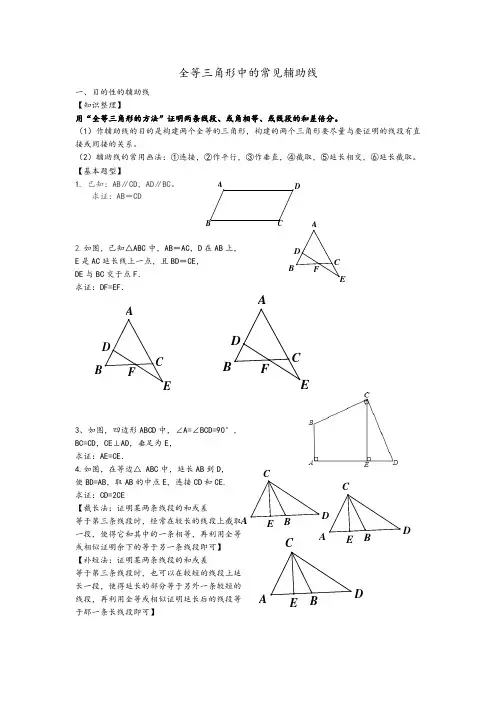
全等三角形中的常见辅助线一、目的性的辅助线 【知识整理】用“全等三角形的方法”证明两条线段、或角相等、或线段的和差倍分。

（1）作辅助线的目的是构建两个全等的三角形，构建的两个三角形要尽量与要证明的线段有直接或间接的关系。

（2）辅助线的常用画法：①连接，②作平行，③作垂直，④截取，⑤延长相交，⑥延长截取。

【基本题型】1. 已知：AB ∥CD ，AD ∥BC 。

求证：AB ＝CD2.如图，已知△ABC 中，AB ＝AC ，D 在AB 上， E 是AC 延长线上一点，且BD ＝CE ， DE 与BC 交于点F ． 求证：DF=EF ．ADBCFA BC EDFA BC EDFA BC ED3、如图，四边形ABCD 中，∠A=∠BCD=90°， BC=CD ，CE⊥AD，垂足为E ， 求证：AE=CE ．4.如图，在等边△ ABC 中，延长AB 到D ， 使BD=AB ，取AB 的中点E ，连接CD 和CE.求证：CD=2CE【截长法：证明某两条线段的和或差等于第三条线段时，经常在较长的线段上截取 一段，使得它和其中的一条相等，再利用全等 或相似证明余下的等于另一条线段即可】 【补短法：证明某两条线段的和或差等于第三条线段时，也可以在较短的线段上延 长一段，使得延长的部分等于另外一条较短的 线段，再利用全等或相似证明延长后的线段等 于那一条长线段即可】5.如图，△ABC 中，∠C ＝2∠B ，∠1＝∠2。

求证：AB ＝AC ＋CDCABDECABDECABDE21ABCD二、探究性的常作辅助线1.角平分线：（1）作角的两边的垂线，使用“角平分线的点到角两边的距离相等” （2）作一边的平行线，使用“平行线的性质、等腰三角形的性质” （3）在角的两边截取相等的线段，构造全等三角形例：已知：△ABC 的∠B 、∠C 的外角平分线交于点P 。

求证：AP 平分∠BAC21ABCD21AB CDACBP2.中垂线：作辅助线构建“中垂线的基本图案”，使用“线段垂直平分线上的点到线段的两个端点的距离相等”3.等腰三角形：（1）作辅助线构建“三线合一”（2）旋转一定的度数，构造全都三角形，等腰一般旋转顶角的度数，等边旋转0604.三角形的中线（或中点）：倍长中线（中点），使延长线段与原中线长相等，构造全等三角形。

全等三角形问题中常有的协助线的作法(有答案)总论：全等三角形问题最主要的是结构全等三角形，结构二条边之间的相等，结构二个角之间的相等【三角形协助线做法】图中有角均分线，可向两边作垂线。

也可将图对折看，对称此后关系现。

角均分线平行线，等腰三角形来添。

角均分线加垂线，三线合一试一试看。

线段垂直均分线，常向两头把线连。

要证线段倍与半，延伸缩短可试验。

三角形中两中点，连结则成中位线。

三角形中有中线，延伸中线等中线。

1.等腰三角形“三线合一”法：碰到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延伸线段与原中线长相等，结构全等三角形3.角均分线在三种添协助线4.垂直均分线联络线段两头5.用“截长法”或“补短法” ：碰到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后组成等边三角形7.角度数为 30、60 度的作垂线法：碰到三角形中的一个角为30 度或 60 度，可以从角一边上一点向角的另一边作垂线，目的是组成30-60-90 的特别直角三角形，而后计算边的长度与角的度数，这样能够获得在数值上相等的二条边或二个角。

从而为证明全等三角形创建边、角之间的相等条件。

8.计算数值法：碰到等腰直角三角形，正方形时，或30-60-90 的特别直角三角形，或40-60-80 的特别直角三角形,常计算边的长度与角的度数，这样能够获得在数值上相等的二条边或二个角，从而为证明全等三角形创建边、角之间的相等条件。

常有协助线的作法有以下几种：最主要的是结构全等三角形，结构二条边之间的相等，二个角之间的相等。

1)碰到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思想模式是全等变换中的“对折”法结构全等三角形．2)碰到三角形的中线，倍长中线，使延伸线段与原中线长相等，结构全等三角形，利用的思想模式是全等变换中的“旋转”法结构全等三角形．3)碰到角均分线在三种添协助线的方法，（1）能够自角均分线上的某一点向角的两边作垂线，利用的思想模式是三角形全等变换中的“对折” ，所考知识点经常是角均分线的性质定理或逆定理．（ 2）能够在角均分线上的一点作该角均分线的垂线与角的两边订交，形成一对全等三角形。

全等三角形六种辅助线方法及例题全等三角形是初中数学中一个非常重要的概念，掌握全等三角形的判定方法和辅助线方法对于解题至关重要。

本文将介绍全等三角形的六种辅助线方法，并结合例题进行详细讲解。

一、辅助线法1.等角分线法：将三角形内角的平分线相互交点构成的点与三角形的另外一个顶点相连，得到一条辅助线。

这条辅助线将三角形分成两个等角的小三角形，从而得到相似或全等三角形。

2.中线法：将三角形任意两边的中点相连，得到三角形的中线。

相等的中线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

3.高线法：将三角形内任意一条边的垂线向另外两边引出，得到三角形的高线。

相等的高线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

4.角平分线法：将三角形内角的平分线相互交点构成的点相连，得到三角形的角平分线。

相等的角平分线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

5.角平分线中垂线法：将三角形内角的平分线的中垂线相互交点构成的点相连，得到三角形的角平分线中垂线。

相等的角平分线中垂线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

6.外心连线法：将三角形外接圆心与三角形三个顶点分别相连，得到三条辅助线。

这三条辅助线相等，将三角形分成三个面积相等的小三角形，从而得到相似或全等三角形。

二、例题解析1.已知△ABC，点D,E分别为BC,AB边上的中点，连接AD，BE相交于点F，求证：△DEF≌△ABC。

解析：由题意可知，△ABC是由两个等腰三角形组成的，因此可使用中线法证明两个三角形的全等。

由于D，E分别是BC,AB边上的中点，因此DE是AC中线，即DE=1/2AC；同理，AE是BC中线，AF=1/2BC。

因此，△ADB和△AEC是等腰三角形，且AD=EC，AB=AB，∠BAC=∠BAC，因此△ADB≌△AEC。

又因为DE是AC中线，BF是AE中线，因此DE=1/2AC，BF=1/2AE。

三角形全等证明常见做辅助线方法一、遇到三角形中线时常见的辅助线若遇到三角形的中线，可倍长中线，使延长线段与原中线长相等，构造全等三角形。

（倍长中线法或“旋转”全等）1、如图，AD 为 △ABC 的中线，求证：AB ＋AC ＞2AD 。

（三角形一边上的中线小于其他两边之和的一半）2、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 。

3、如图，已知：AD 是△ABC 的中线，且CD=AB ，AE 是△ABD 的中线，求证：AC=2AE.C二、遇到角平分线时常见的辅助线1.角平分线上点向角两边作垂线构造全等 过角平分线上一点向角两边作垂线，利用角平分线上的点到角两边距离相等的性质来证明问题。

（作垂线）2.截取构造全等（截长法、补短法）如图1-1，∠AOC=∠BOC ，如取OE=OF ，并连接DE 、DF ，则有△OED ≌△OFD ，从而为我们证明线段、角相等创造了条件。

ADBC图1-1B3.延长垂线段（延长法）遇到垂直于角平分线的线段，则延长该线段与角的另一边相交，构成等腰三角形。

4.作平行线①、以角平分线上一点作角的另一边的平行线，构造等腰三角形，图4-1。

②、通过一边上的点作角平分线的平行线与另外一边的反向延长线相交，从而也构造等腰三角形，图4-2。

图4-2图4-1ABCBIG4、已知：如图2-6,在正方形ABCD 中，E 为CD 的中点，F 为BC上的点，∠FAE=∠DAE 。

求证：AF=AD+CF 。

5、已知CE 、AD 是△ABC 的角平分线，∠B=60°，求证：AC=AE+CD6、已知：如图在△ABC 中，∠A=90°，AB=AC ，BD 是∠ABC 的平分线，求证：BC=AB+AD三、截长补短法（适合于证明线段的和、差、倍、分等类题目）截长法：在长线段上截取与两条线段中的一条相等的一段，证明剩余的线段与另一段相 等（截取----全等----等量代换）图2-6ECDABCD AEBDC补短法：延长其中一短线段使之与长线段相等，再证明延长段与另一短线段相等（延长----全等----等量代换）①、对于证明有关线段和差的不等式，通常会联系到三角形中两线段之和大于第三边、之差小于第三边，故可想办法将其放在一个三角形中证明。

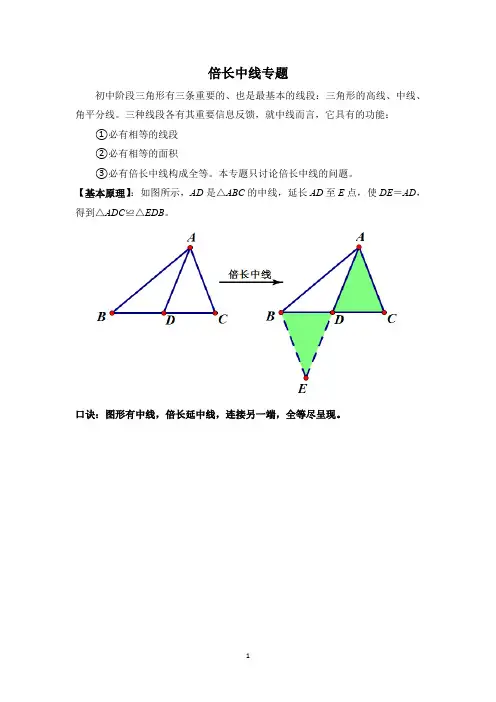
倍长中线专题初中阶段三角形有三条重要的、也是最基本的线段：三角形的高线、中线、角平分线。

三种线段各有其重要信息反馈，就中线而言，它具有的功能：①必有相等的线段②必有相等的面积③必有倍长中线构成全等。

本专题只讨论倍长中线的问题。

【基本原理】：如图所示，AD是△ABC的中线，延长AD至E点，使DE＝AD，得到△ADC≌△EDB。

口诀：图形有中线，倍长延中线，连接另一端，全等尽呈现。

【模型实例】：如图，在△ABC 中，AD 是BC 边的中线，E 是AD 上一点，连接BE 并延长交AC 于F 点，AF=EF ，求证：AC=BE证明： 如图所示。

延长AD 至G 点，使DG=AD ，连接BG 。

在△ADC 与△GDB 中，⎪⎩⎪⎨⎧=∠=∠=CD BD GDB ADC GD AD∴△ADC ≌△GDB∴BG =AC ，∠1=∠G又因为AF=EF∴∠1=∠2=∠3∴∠3=∠G∴BG=BE （等角对等边）∴AC=BE②证全等①作倍长中线 ③列出需要用的结果④转化替代 ⑤得出结果【练习1】：如图，在在△ABC中，D为BC的中点，求证：AD+>AB2AC【练习2】：如图，在△ABC中，D为B C的中点,且AD是角平分线。

求证：AB=AC【练习3】：AD是△ABC的中线，分别以AB边、AC边为直角边向外作等腰直角三角形，求证：EF=2AD【练习4】：在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于F点。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论。

截长补短专题要证明两条线段之和等于第三条线段，可以采用“截长补短”法。

①截长法：把较长的线段截取一段等于两较短线中的一条；②补短法：把两条较短的线段补成一条，再证与长线段相等。

【模型实例】：如图，△ABC中，∠1=∠2，∠B=2∠C。

求证：AC=AB+BD 方法一：截长(利用角平分线构建全等三角形)分析：如图，在AC上截AE=AB，连接DE。

全等三角形几种常见辅助线精典题型一、截长补短1、已知ABC中， A 60o，BD、CE分别平分ABC和.ACB，BD、CE交于点O , 试判断BE、CD、BC的数量关系，并加以证明.2、如图，点M为正三角形ABD的边AB所在直线上的任意一点（点B除外），作DMN 60 ,射线MN与/ DBA外角的平分线交于点N , DM与MN有怎样的数量关系？3、如图，AD 丄AB, CB丄AB, DM = CM= a , AD= h , CB= k，/AMD =75 ZBMC=45 °，求AB 的长4、已知：如图，ABCD是正方形，/ FAD= /FAE求证：BE+DF=AE.B D C连结CD 、BE 相交于点 0 .求证： OA 平分 DOE .6、如图所示，ABC 是边长为1的正三角形，BDC 是顶角为120的等腰三角形, 以D 为顶点作一个60的MDN ，点M 、N 分别在AB 、AC 上, 求AMN 的周长.7、如图所示，在 ABC 中，AB AC , D 是底边BC 上的一点，E 是线段AD 上的一 点，且 BED 2 CED BAC ，求证 BD 2CD .5、以ABC 的AB 、AC 为边向三角形外作等边 ABD 、 ACE ,DFCEE8、 五边形 ABCDE 中，AB =AE , BC +DE 二 CD ,/ABC + ZAED =180 °，求证：AD 平分/CDE二、全等与角度1、如图，在ABC 中, 的度数•3、在正 ABC 内取一点 D ，使DA DB ，在 ABC 外取一点 E ，使 DBE DBC ，且BE BA ，求 BED .BAC 60， AD 是 BAC 的平分线，且 AC AB BD ，求 ABC2、如图所示，在ABC 中，AC BC ，BC 上，且满足 BAN 50 ，C 20，又M 在AC 上，N 在ABM 60，求 NMB .4、如图所示，在ABC中，BAC BCA 44 , M为ABC内一点，使得MCA 30 , MAC 16，求BMC的度数.5、如图：在ABC 内取一点M，使得MBA 30o, MAB 10o.设ACB 80o, AC BC , 求AMC .6、如图，点M为正方形ABCD的边AB上任意一点，MN DM且与/ABC外角的平分线交于点N , MD与MN有怎样的数量关系？如是正五边形，正六边形呢？D C参考答案：一、截长补短1、BE CD BC,理由是：在BC上截取BF BE，连结OF ,利用SAS证得BEO也BFO，二1 2 ,A 60，•/BOC190o -2A 120°，•/ DOE 120°，A DOE 180o，/• AEO ADO 180°，•/ 1 3 180°，2 4 180 o，•/12，••- 3 4，利用AAS证得CDO 也CFO，二CD CF ,二BC BF CF2、DM MN.过点M 作MG II BD 交AD 于点G , AG AM GD MB 又•••/ ADM DMA 120°, / DMA / NMB 120°/•Z ADMZ NMB，而/ DGM / MBN 120°,二DGM 也MBN ,/• DM MN •3、过点D作BC的垂线，垂足为E.vZ AMD =75。

全等三角形几种常见辅助线精典题型This model paper was revised by the Standardization Office on December 10, 2020全等三角形几种常见辅助线精典题型一、截长补短1、已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．2、如图，点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外)，作60DMN ∠=︒，射线MN 与DBA ∠外角的平分线交于点N ，DM 与MN 有怎样的数量关系 3、如图，AD ⊥AB ，CB ⊥AB ，DM =CM =a ，AD =h ，CB =k ，∠AMD =75°，∠BMC =45°，求AB 的长。

4、已知：如图，ABCD 是正方形，∠FAD =∠FAE . 求证：BE +DF =AE .5、以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆，连结CD 、BE 相交于点O ．求证：OA 平分DOE ∠．6、如图所示，ABC ∆是边长为1的正三角形，BDC ∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．7、如图所示，在ABC ∆中，AB AC =，D 是底边BC 上的一点，E 是线段AD 上的一点，且2BED CED BAC ∠=∠=∠，求证2BD CD =.8、五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°，求证：AD 平分∠CDE二、全等与角度NEB M ADDO ECBAMDCBANMDCBAED CBACEDBA1、如图，在ABC ∆中，60BAC ∠=︒，AD 是BAC ∠的平分线，且AC AB BD =+，求ABC ∠的度数.2、如图所示，在ABC ∆中，AC BC =，20C ∠=︒，又M 在AC 上，N 在BC 上，且满足50BAN ∠=︒，60ABM ∠=︒，求NMB ∠.3、 在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.4、如图所示，在ABC ∆中，44BAC BCA ︒∠=∠=，M 为ABC ∆内一点，使得30MCA ︒∠=，16MAC ︒∠=，求BMC ∠的度数.5、如图：在ABC ∆内取一点M ，使得MBA ∠=30，10MAB ∠=.设80ACB ∠=，AC BC =，求AMC ∠.6、如图，点M 为正方形ABCD 的边AB 上任意一点，MN DM ⊥且与ABC ∠外角的平分线交于点N ，MD 与MN 有怎样的数量关系如是正五边形，正六边形呢参考答案：一、截长补短1、BE CD BC +=，理由是：在BC 上截取BF BE =，连结OF ，利用SAS 证得BEO ∆≌BFO ∆，∴12∠=∠，∵60A ∠=︒，∴1901202BOC A ∠=+∠=，∴120DOE ∠=，∴180A DOE ∠+∠=，∴180AEO ADO ∠+∠=，∴13180∠+∠=，NMCBA4321FD OE CBA∵24180∠+∠=，∴12∠=∠，∴34∠=∠，利用AAS 证得CDO ∆≌CFO ∆，∴CD CF =，∴BC BF CF BE CD =+=+．2、DM MN =.过点M 作MG BD ∥交AD 于点G ，AG AM =，∴GD MB =又∵120ADM DMA +∠=∠，120DMA NMB +=∠∠∴ADM NMB =∠∠，而120DGM MBN ==∠∠，∴DGM MBN ∆∆≌，∴DM MN =．3、过点D 作BC 的垂线，垂足为E .∵∠AMD =75°，∠BMC =45° ∴∠DMC =60°∵DM =CM ∴CD =DM∵AD ⊥AB ，DE ⊥BC ，CB ⊥AB ，∠AMD =75°∴∠ADM =∠EDC ∴△ADM ≌△CDE ∴AD =DE故ABED 为正方形，AB =AD =h ，选D .4、延长CB 至M ，使得BM =DF ，连接AM .E MDCBAM F EDCB A∵AB =AD ，AD ⊥CD ，AB ⊥BM ，BM =DF ∴△ABM ≌△ADF∴∠AFD =∠AMB ，∠DAF =∠BAM ∵AB ∥CD∴∠AFD =∠BAF =∠EAF +∠BAE =∠BAE +∠BAM =∠EAM∴∠AMB =∠EAM ∴AE =EM =BE +BM =BE +DF .5、因为ABD ∆、ACE ∆是等边三角形，所以AB AD =，AE AC =，CAE ∠=60BAD ∠=，则BAE DAC ∠=∠，所以BAE DAC ∆∆≌， 则有ABE ADC ∠=∠，AEB ACD ∠=∠，BE DC =．在DC 上截取DF BO =，连结AF ，容易证得ADF ABO ∆∆≌，ACF AEO ∆∆≌． 进而由AF AO =．得AFO AOF ∠=∠；由AOE AFO ∠=∠可得AOF ∠=AOE ∠，即OA 平分DOE ∠． 6、如图所示，延长AC 到E 使CE BM =.在BDM ∆与CDE ∆中，因为BD CD =，90MBD ECD ∠=∠=，BM CE =， 所以BDM CDE ∆∆≌，故MD ED =.EABC DM N因为120BDC ∠=，60MDN ∠=，所以60BDM NDC ∠+∠=. 又因为BDM CDE ∠=∠，所以60MDN EDN ∠=∠=.在MND ∆与END ∆中，DN DN =，60MDN EDN ∠=∠=，DM DE =， 所以MND END ∆∆≌，则NE MN =，所以AMN ∆的周长为2.7、如图所示，作BED ∠的平分线交BC 于F ，又过A 作AH EF ∥交BE 于G ，交BC 于H ，则知12EAG DEF BEF AGE BAC ∠=∠=∠=∠=∠，从而GE AE =.又12AGE BED CED ∠=∠=∠，则AGB CEA ∠=∠.由ABE BAE BED BAC CAE BAE ∠+∠=∠=∠=∠+∠可得ABG CAE ∠=∠. 注意到AB CA =，故有ABG CAE ∆∆≌，从而BG AE =，AG CE =，于是BG GE =.又由AH EF ∥，有BH HF =，12GH EF =，且AH HDEF FD=. 而CED FED ∠=∠，从而1122CD EC AG AH GH AH HD FD EF EF EF EF FD -====-=-， 即1111122222CD HD FD HF FD BF FD BD =-=+=+=，故2BD CD =.8、延长DE 至F ，使得EF =BC ，连接AC .∵∠ABC +∠AED =180°，∠AEF +∠AED =180° ∴∠ABC =∠AEFGH F ED CB A∵AB=AE，BC=EF∴△ABC≌△AEF∴EF=BC，AC=AF∵BC+DE=CD∴CD=DE+EF=DF∴△ADC≌△ADF∴∠ADC=∠ADF即AD平分∠CDE.二、全等与角度1、如图所示，延长AB至E使BE BD=，连接ED、EC.由AC AB BD=+知AE AC=，而60BAC∠=，则AEC∆为等边三角形.注意到EAD CAD∠=∠，AD AD=，AE AC=，故AED ACD∆∆≌.从而有DE DC=，DEC DCE∠=∠，故2BED BDE DCE DEC DEC∠=∠=∠+∠=∠.所以20DEC DCE∠=∠=，602080ABC BEC BCE∠=∠+∠=+=【另解】在AC上取点E，使得AE AB=，则由题意可知CE BD=.在ABD∆和AED∆中，AB AE=，BAD EAD∠=∠，ABD EFCED C BAED C BAAD AD =，则ABD AED ∆∆≌，从而BD DE =，进而有DE CE =，ECD EDC ∠=∠，AED ECD EDC ∠=∠+∠=2ECD ∠.注意到ABD AED ∠=∠，则：1318012022ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=-∠=，故80ABC ∠=︒.【点评】由已知条件可以想到将折线ABD “拉直”成AE ，利用角平分线AD 可以构造全等三角形.同样地，将AC 拆分成两段，之后再利用三角形全等亦可，此思路也是十分自然的.需要说明的是，无论采取哪种方法，都体现出关于角平分线“对称”的思想.上述方法我们分别称之为“补短法”和“截长法”，它们是证明等量关系时优先考虑的方法.2、过M 作AB 的平行线交BC 于K ，连接KA 交MB 于P .连接PN ，易知APB ∆、MKP ∆均为正三角形. 因为50BAN ∠=︒，AC BC =，20C ∠=︒，所以50ANB ∠=︒，BN AB BP ==，80BPN BNP ∠=∠=︒，则40PKN ∠=︒，180608040KPN ∠=︒-︒-︒=︒， 故PN KN =. 从而MPN MKN ∆∆≌.进而有PMN KMN ∠=∠，1302NMB KMP ∠=∠=︒3、如图所示，连接DC .因为AD BD =，AC BC =，CD CD =， 则ADC BDC ∆∆≌，故30BCD ∠=.而DBE DBC ∠=∠，BE AB BC ==，BD BD =，因此BDE BDC ∆∆≌， 故30BED BCD ∠=∠=.4、在ABC ∆中，由44BAC BCA ︒∠=∠=可得AB AC =，92ABC ︒∠=. 如图所示，作BD AC ⊥于D 点，延长CM 交BD 于O 点，连接OA ，则有30OAC MCA ︒∠=∠=，443014BAO BAC OAC ︒︒︒∠=∠-∠=-=，301614OAM OAC MAC ︒︒︒∠=∠-∠=-=，所以BAO MAO ∠=∠.又因为90903060AOD OAD COD ︒︒︒︒∠=-∠=-==∠， 所以120AOM AOB ∠=︒=∠.120BOM ∠=︒DECBAOD MCA B而AO AO =，因此ABO AMO ∆∆≌，故OB OM =.由于120BOM ︒∠=，则180302BOMOMB OBM ︒-∠∠=∠==︒，故180150BMC OMB ︒︒∠=-∠=5、如图所示，ABC ∆的高CH 与直线BM 交于点E ，则AE BE =. 而301020EAM EAB MAB ∠=∠-∠=-=，1402ACE ACB ∠=∠=，(9040)3020EAC CAH EAB ∠=∠-∠=--=，103040AME MAB MBA ∠=∠+∠=+=，由两角夹一边法则可知AME ACE ∆∆≌， 因此AM AC =，6、DM MN =.在AD 上截取AG AM =，∴DG MB =，∴45AGM =∠∴135DGM MBN ==︒∠∠，∴ADM NMB =∠∠， ∴DGM MBN ∆∆≌，∴DM MN =．EHABCMNCDEB M A。

全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”：遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。

从而为证明全等三角形创造边、角之间的相等条件。

8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。

常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。

1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”法构造全等三角形．3)遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。

全等三角形常见辅助线做法
（1）在△ABC中，如AD是中线，常采用的作法是：
①延长AD到E，使DE＝AD，连结BE（或过B作BE∥AC，交AD的延长线于E），如图甲。

②取AC的中点E，连结DE（或过D作DE∥BA，交AC于E），如图乙。

③延长BA至E，使AE＝AB，连结CE（或过C作CE∥AD交BA的延长线于E），如图丙。

（2）在△ABC中，若AD是∠BAC的平分线，常采用的作法是：
①延长BA至E，使AE＝AC，连结CE（或过C作CE∥AD，交BA的延长线于E），如图甲。

②在较长边AB上截取AE＝AC，连结DE，如图乙。

③过C作CE∥AB，交AD的延长线于E，如图丙。

④过D作DE∥AB，交AC于E，如图丁。

（3）在△ABC中，若D是AB的中点，常采用的作法是：
①过D作DE∥BC，交AC于E。

②取AC的中点E，连结DE。

③连结CD，用中线的性质。

④若已知△ABC为特殊三角形，可利用特殊三角形的性质：如为等腰三角形，考虑顶点平分线；若为直角三角形，考虑斜边中线；若为有一个角是30°的直角三角形，考虑斜边中线及30°角所对边之间的关系，常可作出中线。

全等三角形几何证明常用辅助线
辅助线证明三角形全等
一、辅助线定义
辅助线，又称辅助规则，是专门用来证明几何结论的辅助线，它可以
指向几何结论的前提或结果，以更清晰地证明几何结论。

二、辅助线用法
1.在证明三角形全等的情况下，用辅助线来证明角的相等性：用一条
辅助线平分角A，然后将辅助线平移到角B上，如果辅助线可以在角B上
的两点重合，则说明角A和角B是相等的。

2.在证明三角形全等的情况下，用辅助线来证明边的相等性：用一条
辅助线平分边AB，然后将辅助线平移到边CD上，如果辅助线可以在边CD
上的两点重合，则说明边AB和边CD是相等的。

3.在证明三角形全等的情况下，用辅助线来证明两个三角形的相等性：在三角形ABC中画出一条辅助线，然后将该辅助线平移到三角形CDE中，
如果辅助线可以在三角形CDE中的三个点重合，则说明两个三角形ABC和CDE是相等的。

三、辅助线证明三角形全等的步骤
1.识别出待证明的相关图形，并将其准确地表示在平面上。

2.根据定义，确定三角形全等的前提条件，并假设三角形全等。

3.画出两个三角形之间的辅助线，如果相交点都在两个三角形相交的
边上，证明该辅助线可以同时在两个三角形中存在。

全等三角形六种辅助线方法全等三角形是指具有相同形状和大小的三角形。

在解决与全等三角形相关的问题时，辅助线是一种常用的方法，可以帮助我们更好地理解和解决问题。

下面将介绍全等三角形的六种辅助线方法。

一、垂直辅助线法垂直辅助线法是指通过某个顶点引一条垂直线与对边相交，从而将三角形分割成两个直角三角形。

利用直角三角形的性质，我们可以更方便地求解各种问题。

二、角平分线法角平分线法是指通过某个顶点引一条角平分线与对边相交，将三角形分割成两个等角的三角形。

利用等角三角形的性质，我们可以更容易地求解各种问题。

三、高线法高线法是指通过某个顶点引一条垂直于底边的线段，将三角形分割成一个直角三角形和一个等腰三角形。

利用这两个三角形的性质，我们可以更快速地解决问题。

四、中线法中线法是指连接三角形的两个顶点和底边中点，将三角形分割成三个相似的三角形。

利用相似三角形的性质，我们可以更高效地解决问题。

五、中垂线法中垂线法是指通过三角形的每条边的中点引一条垂直于对边的线段，将三角形分割成三个直角三角形。

利用直角三角形的性质，我们可以更轻松地解决问题。

六、对称线法对称线法是指通过三角形的某个顶点引一条对称线，将三角形分割成两个全等的三角形。

利用全等三角形的性质，我们可以更直接地解决问题。

通过以上六种辅助线方法，我们可以更灵活地分析和解决与全等三角形相关的问题。

这些方法使得计算更加简便，推理更加直观，提高了问题解决的效率。

同时，这些方法也加深了我们对全等三角形的理解，拓宽了我们的数学思维。

在实际应用中，我们可以根据具体问题的要求选择合适的辅助线方法，以便更好地解决问题。

全等三角形的六种辅助线方法是垂直辅助线法、角平分线法、高线法、中线法、中垂线法和对称线法。

这些方法在解决与全等三角形相关的问题时起到了重要的作用，使我们能够更快速、准确地解决问题。

希望通过这篇文章的介绍，能够帮助大家更好地理解和应用这些方法。

全等三角形常见辅助线作法知识结构图一．中点类辅助线作法见到中线(中点)，我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段，尤其是在涉及线段的等量关系时，倍长中线的应用更是较为常见，常见添加方法如下图（是底边的中线)．二．角平分线类辅助线作法有下列三种作辅助线的方式：1．由角平分线上的一点向角的两边作垂线；2．过角平分线上的一点作角平分线的垂线，从而形成等腰三角形；3．，这种对称的图形应用得也较为普遍．三．截长补短类辅助线作法截长补短法，是初中数学几何题中一种辅助线的添加方法，也是把几何题化难为易的一种思想．所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段等于已知的两条较短线段中的一条，然后证明其中的另一段与已知的另一条线段相等；所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等，然后求出延长后的线段与最长的已知线段的关系．有的是采取截长补短后，使之构成某种特定的三角形进行求解．四．型图（一线三等角）型图是最重要的几何模型之一，在证明三角形全等、相似，求点的坐标时有着重要的应用．（1）如图，已知，，，；则，，．（2）型图变化：将向右移动会出现下面两种情况：①如图，已知，，，，，则，；②如图，已知，，，，，则，．题模一中点类全等问题例1.1、如图，已知在中，是边上的中线，是上一点，延长交于，，求证：．例1.2、在中，，点为的中点，点、分别为、上的点，且．以线段、、为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形或钝角三角形？例1.3、八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．【探究与发现】（1）如图1，AD是△ABC的中线，延长AD至点E，使ED=AD，连接BE，写出图中全等的两个三角形______ 【理解与应用】（2）填空：如图2，EP是△DEF的中线，若EF=5，DE=3，设EP=x，则x的取值范围是______．（3）已知：如图3，AD是△ABC的中线，∠BAC=∠ACB，点Q在BC的延长线上，QC=BC，求证：AQ=2AD．例1.4、在△ABC中，D为BC边的中点，在三角形内部取一点P，使得．过点P作PE⊥AC于点E，PF⊥AB于点F．（1）如图1，当时，判断的DE与DF的数量关系，直接写出你的结论；（2）如图2，当，其它条件不变时，（1）中的结论是否发生改变？请说明理由．题模二角平分线类全等问题例2.1、中，AD是的平分线，且．若，则的大小为（）A、40°B、60°C、80°D、100°例2.2、如图所示，在△ABC中，，AD是∠BAC的平分线，BE⊥AD于F．求证：．例2.3、已知，AC平分∠MAN，点B、D分别在AN、AM上．（1）如图1，若，请你探索线段AD、AB、AC之间的数量关系，并证明之；（2）如图2，若，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．题模三截长补短类全等问题例3.1、如图所示，是边长为的正三角形，是顶角为的等腰三角形，以为顶点作一个的，点、分别在、上，求的周长．例3.2、(2013初二上期中人民大学附属中学)如图，△ABC中，，AD是BC边上的高，如果，我们就称△ABC为“高和三角形”．请你依据这一定义回答问题：（1）若，，则△ABC____ “高和三角形”（填“是”或“不是”）；（2）一般地，如果△ABC是“高和三角形”，则与之间的关系是____，并证明你的结论例3.3、（1）如图，四边形ABPC中，，，，求证：．（2）如图，四边形ABCD中，，，P为四边形ABCD内一点，且，求证：．题模四K型图例4.1、如图，在等腰中，，为的中点，，垂足为，过点作交的延长线于点，连接．（1）求证：；（2）连接，求证：．例4.2、如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是线段BC上一点，以AE为边在直线MN的上方作正方形AEFG（1）连接GD，求证：；（2）连接FC，求证：，并说明理由；（3）当E点在CB的延长线上时，如图（2），连接FC，则等于多少度？请说明理由．例4.3、如图（1），已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一条直线，且B、C在A、E的异侧，BD ⊥AE于D，CE⊥AE于E（1）试说明：BD=DE+CE．（2）若直线AE绕A点旋转到图（2）位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果；（3）若直线AE绕A点旋转到图（3）位置时（BD＞CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果，不需说明理由．随堂练习随练1.1、如图所示，是等腰直角三角形，，是边上的中线，过作的垂线，交于点，交于点，求证：．随练1.2、如图，在△ABC中，AD是△ABC的角平分线，AB=4，BD=3，∠B=2∠C，则AC的长为（）A、 6B、 7C、 8D、9随练1.3、如图所示，在中，，延长到，使，为的中点，连接、，求证：．随练1.4、如图，在中，D为BC边上的中点，AE平分交BC于E，交AC于F，，，求CF的长．随练1.5、(2013初二上期末怀柔区)（1）已知：如图1，在△ABC中，∠A=90°，D为BC中点，E为AB上一点，F为AC上一点，ED⊥DF，连接EF，求证：线段BE、FC、EF总能构成一个直角三角形；（2）已知：如图2，∠A=120°，D为BC中点，E为AB上一点，F为AC上一点，ED⊥DF，连接EF，请你找出一个条件，使线段BE、FC、EF能构成一个等边三角形，给出证明．随练1.6、已知∠MAN，AC平分∠MAN．（1）在图1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：AB+AD=AC；（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）在图3中：①∠MAN=60°，∠ABC+∠ADC=180°，则AB+AD= AC；②若∠MAN=α（0°＜α＜180°），∠ABC+∠ADC=180°，则AB+AD= AC（用含α的三角函数表示），并给出证明．随练1.7、如图，在△ABC中，，D是三角形外一点，且，．求证：随练1.8、如图，△ABC中，，点P是三角形右外一点，且．（1）如图1，若，点P恰巧在∠ABC的平分线上，，求PB的长；（2）如图2，若，探究PA，PB，PC的数量关系，并证明；（3）如图3，若，请直接写出PA，PB，PC的数量关系．随练1.9、在△DEF中，DE=DF，点B在EF边上，且∠EBD=60°，C是射线BD上的一个动点（不与点B重合，且BC≠BE），在射线BE上截取BA=BC，连接AC．（1）当点C在线段BD上时，①若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系为；②如图2，若点C不与点D重合，请证明AE=BF+CD；（2）当点C在线段BD的延长线上时，用等式表示线段AE，BF，CD之间的数量关系（直接写出结果，不需要证明）．随练1.10、直角三角形有一个非常重要的性质：直角三角形斜边上的中线等于斜边的一半，比如：如图1，Rt△ABC 中，∠C=90°，D为斜边AB中点，则CD=AD=BD=AB．请你利用该定理和以前学过的知识解决下列问题：如图2，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若B、P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM、PN；（1）求证：PM=PN；（2）若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变，此时PM=PN还成立吗？若成立，请给予证明：若不成立，请说明理由；（3）如图4，∠BAC=90°，a旋转到与BC垂直的位置，E为BC上一点且AE=AC，EN⊥a于N，连接EC，取EC中点P，连接PM，PN，求证：PM⊥PN．随练1.11、【问题情境】如图，在正方形ABCD中，点E是线段BG上的动点，AE⊥EF，EF交正方形外角∠DCG的平分线CF于点F．【探究展示】（1）如图1，若点E是BC的中点，证明：∠BAE+∠EFC=∠DCF．（2）如图2，若点E是BC的上的任意一点（B、C除外），∠BAE+∠EFC=∠DCF是否仍然成立？若成立，请予以证明；若不成立，请说明理由．【拓展延伸】（3）如图3，若点E是BC延长线（C除外）上的任意一点，求证：AE=EF．随练1.12、直线过的顶点，．分别是直线上两点，且．（1）若直线经过的内部，且在射线上，请解决下面两个问题：①如图1，若则_______（填“”，“”或“”）；②如图②，若，若使①中的结论任然成立，则与应满足的关系式_______________；（2）如图3，若直线经过的外部，，请探究与三条线段的数量关系，并给予证明．能力拓展拓展1、已知：如图，在中，AD平分，于点D，，若，，求AB的长．拓展2、如图所示，，是的中点，，，求证．拓展3、如图，点为正三角形的边所在直线上的任意一点（点除外），作，射线与外角的平分线交于点，与有怎样的数量关系?拓展4、已知的顶点C在的平分线OP上，CD交OA于F，CE交OB于G．（1）如图1，若，，则图中有哪些相等的线段，请直接写出你的结论：__________；（2）如图2，若，，试判断线段CF与线段CG的数量关系并加以证明；（3）若，当满足什么条件时，你在（2）中得到的结论仍然成立，请直接写出满足的条件．拓展5、如图1，在△ABC中，，∠BAC的平分线AO交BC于点D，点H为AO上一动点，过点H 作直线l⊥AO于H，分别交直线AB、AC、BC于点N、E、M．（1）当直线l经过点C时（如图2），证明：；（2）当M是BC中点时，写出CE和CD之间的等量关系，并加以证明；（3）请直接写出BN、CE、CD之间的等量关系．拓展6、如图，在△ABC中，，，P、Q分别在BC、CA上，并且AP、BQ分别是∠BAC、∠ABC的角平分线．求证：（1）；（2）．拓展7、已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为E、F、Q为斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是__，QE与QF的数量关系是__；（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；（3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．拓展8、在△ABC，∠BAC为锐角，，AD平分∠BAC交BC于点D．（1）如图1，若△ABC是等腰直角三角形，直接写出线段AC，CD，AB之间的数量关系；（2）BC的垂直平分线交AD延长线于点E，交BC于点F．①如图2，若，判断AC，CE，AB之间有怎样的数量关系并加以证明②如图3，若，求∠BAC的度数．拓展9、在平行四边形ABCD中，E是AD上一点，，过点E作直线EF，在EF上取一点G，使得，连接AG．（1）如图1，当EF与AB相交时，若，求证：；（2）如图2，当EF与AB相交时，若，请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；（3）如图3，当EF与CD相交时，且，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．拓展10、在□ABCD中，，过点D作，且，连接EF、EC，N、P分别为EC、BC的中点，连接NP．（1）如图1，若点E在DP上，EF与DC交于点M，试探究线段NP与线段NM的数量关系及∠ABD与∠MNP 满足的等量关系，请直接写出你的结论；（2）如图2，若点M在线段EF上，当点M在何位置时，你在（1）中得到的结论仍然成立，写出你确定的点M的位置，并证明（1）中的结论．拓展11、如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC中，∠ACB是直角，，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，请你判断并写出FE与FD之间的数量关系（不需证明）；（2）如图③，在△ABC中，，请问，在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．拓展12、如图①所示，已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1．（1）如图②，当点E恰好在直线l上时（此时E1与E重合），试说明DD1=AB；（2）在图①中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；（3）如图③，当点E在直线l的下方时，请直接写出三条线段DD1、EE1、AB之间的数量关系．（不需要证明）拓展13、已知△ABC中，M为BC的中点，直线m 绕点A旋转，过B，M，C 分别作BD⊥m于点D，ME⊥m于点E，CF⊥m于点F．当直线m经过点B时，如图1，可以得到．（1）当直线m不经过B点，旋转到如图2，图3 的位置时，线段BD，ME，CF之间有怎样的数量关系，请直接写出你的猜想．图2，猜想：；图3，猜想：．（2）选择第（1）问中任意一种猜想加以证明．拓展14、（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图①，已知：在△ABC中，∠BAC=90°，AB=AC，直线L经过点A，BD⊥直线L，CE⊥直线L，垂足分别为点D、E．证明：①△ABD≌△CAE；②DE=BD+CE．（2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线L上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图③，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点．。

五种辅助线助你证全等姚全刚在证明三角形全等时有时需添加辅助线，对学习几何证明不久的学生而言往往是难点．下面介绍证明全等时常见的五种辅助线，供同学们学习时参考．一、截长补短一般地，当所证结论为线段的和、差关系，且这两条线段不在同一直线上时，通常可以考虑用截长补短的办法：或在长线段上截取一部分使之与短线段相等；或将短线段延长使其与长线段相等．例1．如图1，在△ABC中，∠ABC=60°，AD、CE分别平分∠BAC、∠ACB．求证：AC=AE+CD．分析：要证AC=AE+CD，AE、CD不在同一直线上．故在AC上截取AF=AE，则只要证明CF=CD．证明：在AC上截取AF=AE，连接OF．∵AD、CE分别平分∠BAC、∠ACB，∠ABC=60°∴∠1+∠2=60°，∴∠4=∠6=∠1+∠2=60°．显然，△AEO≌△AFO，∴∠5=∠4=60°，∴∠7=180°－（∠4+∠5）=60°在△DOC与△FOC中，∠6=∠7=60°，∠2=∠3，OC=OC∴△DOC≌△FOC，CF=CD∴AC=AF+CF=AE+CD．截长法与补短法，具体作法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明。

这种作法，适合于证明线段的和、差、倍、分等类的题目。

例2：如图甲，AD∥BC，点E在线段AB上，∠ADE=∠CDE，∠DCE=∠ECB。

求证：CD=AD+BC。

思路分析：1）题意分析：本题考查全等三角形常见辅助线的知识：截长法或补短法。

2）解题思路：结论是CD=AD+BC，可考虑用“截长补短法”中的“截长”，即在CD上截取CF=CB，只要再证DF=DA即可，这就转化为证明两线段相等的问题，从而达到简化问题的目的。

解答过程：证明：在CD上截取CF=BC，如图乙∴△FCE≌△BCE（SAS），∴∠2=∠1。