初中数学之函数图像题必考5种类型,考试必备!

初中数学：函数及其图像易错题归纳
函数是中考数学的重点和难点，因为函数的题型变化太多，可以和很多知识点进行糅合。

但是，我们把最基础的概念完全理解透彻，牢牢掌握。

能够把函数的三种基本形式：一般式，顶点式和交点式的特点和异同特性做到灵活运用。

我们可以通过函数图像的开口方向，对称轴，和坐标系x轴y轴的交点，或者根据抛物线上的点，就可以快速地求出函数的解析式。

考试中求解析式的题目非常常见，特别是在中考的最后一道大题，算作是数学大题中的压轴题。

而对学生来说，抛物线学不好，函数就无从下手，抛物线中的开口问题、对称轴问题、交点问题等充斥大脑，会让很多同学望而却步。

虽然话是这样说，但是学好函数还是有诀窍的，要结合图像说性质，结合性质画图像，正所谓数形结合，函数无敌。

初中数学：掌握这15张函数图，函数真的白捡分，建议家长
珍藏打印
从小学到高中，数学都是学习的大头，初中的数学在整个学习阶段中有限的尤为重要，难点自然也非常多。

但是并不是每一个难点都特别困难，今天我要跟大家分享的就是中考必考的一个知识点：“函数”。

为了帮助同学们更有效地学习，老师将“函数”做了分类讲解，每个知识点都讲得特别细，大家看看就知道了，希望大家不要忽略，吃透基础的，高分自然就来了。

●文末附有电子版资料下载方式
函数只要分清楚三个部分就行了，一次函数，反比例函数，了解清楚他们的图像与性质，弄清楚他们的平面直角坐标系与变量，函数问题就变得一目了然了。

一次函数
反比例函数
二次函数
1. 由抛物线开口方向确定a
1. 由对称轴的位置确定b、ab。

函数图像大全函数图像是数学中的重要概念之一，它可以直观地展现出函数的性质和特点。

在数学教学中，函数图像也是一个重要的教学内容，通过观察函数的图像，可以更好地理解函数的变化规律和特点。

本文将对常见的函数图像进行详细介绍，希望能够帮助读者更好地理解和掌握函数图像的相关知识。

一、线性函数图像。

线性函数是最简单的一类函数，它的图像通常是一条直线。

线性函数的一般形式为y=kx+b，其中k和b为常数，k表示直线的斜率，b表示直线与y轴的交点。

当k大于0时，直线向上倾斜；当k小于0时，直线向下倾斜；当k等于0时，直线平行于x轴。

b的取值决定了直线与y轴的交点的位置。

线性函数的图像特点明显，通过观察直线的斜率和截距，可以快速了解函数的性质。

二、二次函数图像。

二次函数的一般形式为y=ax^2+bx+c，其中a、b、c为常数且a不等于0。

二次函数的图像通常是一个抛物线，其开口方向由a的正负决定。

当a大于0时，抛物线开口向上；当a小于0时，抛物线开口向下。

二次函数的图像特点较为复杂，需要通过求导、配方法等手段来确定抛物线的顶点、焦点等重要特征点。

三、指数函数图像。

指数函数的一般形式为y=a^x，其中a为常数且a大于0且不等于1。

指数函数的图像通常是一条曲线，其特点是随着自变量x的增大，函数值呈指数增长或指数衰减。

指数函数的图像在x轴的左侧逐渐逼近y轴，而在x轴的右侧则迅速增长。

指数函数是一种常见的增长模型，在经济、生物、物理等领域有着广泛的应用。

四、对数函数图像。

对数函数的一般形式为y=loga(x)，其中a为常数且a大于0且不等于1。

对数函数的图像通常是一条曲线，其特点是随着自变量x的增大，函数值呈对数增长。

对数函数的图像在x轴的右侧逐渐逼近y轴，而在x轴的左侧则迅速减小。

对数函数是一种常见的减小模型，在金融、生物、信息论等领域有着广泛的应用。

五、三角函数图像。

三角函数包括正弦函数、余弦函数、正切函数等，它们的图像都具有周期性。

初中知识点归纳——函数图像篇函数图像是初中数学中的重要内容之一。

通过函数图像的形状、特点以及变化规律，可以深入理解函数的性质和作用。

本文将从函数图像的基本形状与分类、常见函数图像的特点及其变化规律等方面进行归纳与总结。

一、函数图像的基本形状与分类函数图像的形状可以分为线性函数、二次函数、指数函数和对数函数等几种常见类型。

1. 线性函数图像线性函数的特点是图像为一条直线。

直线的斜率表示了函数的增减趋势，当斜率为正时，函数图像呈上升趋势；当斜率为负时，函数图像呈下降趋势；斜率为0时，函数图像为水平直线。

2. 二次函数图像二次函数的图像通常为抛物线形状。

抛物线的开口方向由二次项的系数决定，当二次项的系数为正时，抛物线开口向上；当二次项的系数为负时，抛物线开口向下。

二次函数的图像还受到常数项的影响，常数项决定了抛物线的位置。

3. 指数函数图像指数函数的图像为指数曲线，呈现上升或下降的趋势。

指数函数的底数决定了曲线在坐标系中的位置和形状。

当底数大于1时，指数曲线呈现上升趋势；当底数小于1但大于0时，指数曲线呈现下降趋势。

4. 对数函数图像对数函数的图像为对数曲线，也呈现上升或下降的趋势。

对数函数的底数决定了曲线在坐标系中的位置和形状。

当底数大于1时，对数曲线呈现上升趋势；当底数小于1但大于0时，对数曲线呈现下降趋势。

二、常见函数图像的特点与变化规律1. 线性函数的特点与变化规律线性函数的图像为一条直线，具有以下特点和变化规律：（1）斜率决定了线性函数图像的倾斜程度和方向，斜率越大图像越陡峭，斜率为正表示函数图像上升，斜率为负表示函数图像下降。

（2）截距决定了线性函数图像与纵轴的交点位置，截距为正表示交点在纵轴上方，截距为负表示交点在纵轴下方。

2. 二次函数的特点与变化规律二次函数的图像为抛物线，具有以下特点和变化规律：（1）开口方向由二次项的系数决定，正系数表示抛物线开口向上，负系数表示抛物线开口向下。

（2）顶点是抛物线的最高点或最低点，在坐标系中的横坐标为顶点的x坐标，纵坐标为顶点的y坐标。

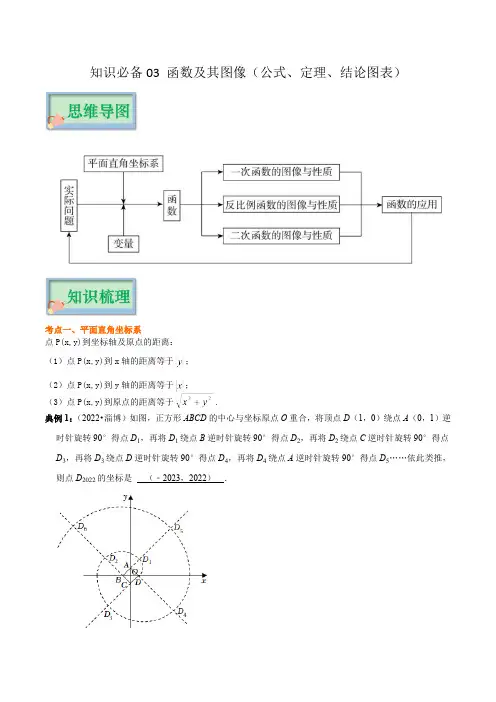
知识必备03 函数及其图像（公式、定理、结论图表）考点一、平面直角坐标系点P(x,y)到坐标轴及原点的距离：（1）点P(x,y)到x轴的距离等于；（2）点P(x,y)到y轴的距离等于；（3）点P(x,y)到原点的距离等于.典例1：（2022•淄博）如图，正方形ABCD的中心与坐标原点O重合，将顶点D（1，0）绕点A（0，1）逆时针旋转90°得点D1，再将D1绕点B逆时针旋转90°得点D2，再将D2绕点C逆时针旋转90°得点D3，再将D3绕点D逆时针旋转90°得点D4，再将D4绕点A逆时针旋转90°得点D5……依此类推，则点D2022的坐标是　（﹣2023，2022）　．【分析】由题意观察发现：每四个点一个循环，D4n+2（﹣4n﹣3，4n+2），由2022＝505×4+2，推出D2022（﹣2023，2022）．【解答】解：∵将顶点D（1，0）绕点A（0，1）逆时针旋转90°得点D1，∴D1（1，2），∵再将D1绕点B逆时针旋转90°得点D2，再将D2绕点C逆时针旋转90°得点D3，再将D3绕点D逆时针旋转90°得点D4，再将D4绕点A逆时针旋转90°得点D5……∴D2（﹣3，2），D3（﹣3，﹣4），D4（5，﹣4），D5（5，6），D6（﹣7，6），……，观察发现：每四个点一个循环，D4n+2（﹣4n﹣3，4n+2），∵2022＝4×505+2，∴D2022（﹣2023，2022）；故答案为：（﹣2023，2022）．【点评】本题考查坐标与图形的变化﹣旋转，等腰直角三角形性质，规律型问题，解题的关键是学会探究规律的方法，属于中考选择题中的压轴题．考点二、函数及其图象由函数解析式画其图像的一般步骤：（1）列表：列表给出自变量与函数的一些对应值；（2）描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；（3）连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来.考点三、一次函数确定一个正比例函数，就是要确定正比例函数定义式（k0）中的常数k；确定一个一次函数，典例2：（2022•柳州）如图，直线y1＝x+3分别与x轴、y轴交于点A和点C，直线y2＝﹣x+3分别与x轴、y轴交于点B和点C，点P（m，2）是△ABC内部（包括边上）的一点，则m的最大值与最小值之差为（ ）A．1B．2C．4D．6【分析】由于P的纵坐标为2，故点P在直线y＝2上，要求符合题意的m值，则P点为直线y＝2与题目中两直线的交点，此时m存在最大值与最小值，故可求得．【解答】解：∵点P（m，2）是△ABC内部（包括边上）的一点，∴点P在直线y＝2上，如图所示，当P为直线y＝2与直线y2的交点时，m取最大值，当P为直线y＝2与直线y1的交点时，m取最小值，∵y2＝﹣x+3中令y＝2，则x＝1，y1＝x+3中令y＝2，则x＝﹣1，∴m的最大值为1，m的最小值为﹣1．则m的最大值与最小值之差为：1﹣（﹣1）＝2．故选：B．【点评】本题考查一次函数的性质，要求符合题意的m值，关键要理解当P在何处时m存在最大值与最小值，由于P的纵坐标为2，故作出直线y＝2有助于判断P的位置．需要确定一次函数定义式（k0）中的常数k和b.解这类问题的一般方法是待定系数法.典例3：（2022•沈阳）如图，在平面直角坐标系中，一次函数y＝kx+b的图象与x轴交于点A，与y轴交于点B（0，9），与直线OC交于点C（8，3）．（1）求直线AB的函数表达式；（2）过点C作CD⊥x轴于点D，将△ACD沿射线CB平移得到的三角形记为△A′C′D′，点A，C，D的对应点分别为A′，C′，D′，若△A′C′D′与△BOC重叠部分的面积为S，平移的距离CC′＝m，当点A′与点B重合时停止运动．①若直线C′D′交直线OC于点E，则线段C′E的长为　m　（用含有m的代数式表示）；②当0＜m＜时，S与m的关系式为　m2　；③当S＝时，m的值为　或15﹣2　．【分析】（1）将点B（0，9），C（8，3）的坐标代入直线解析式，求解即可；（2）①过点C作CF⊥C′D′，易得△CFC′∽△AOB，可用m表达CF和C′F的长度，进而可表达点C′，D′的坐标，由点C的坐标可得出直线OC的解析式，代入可得点E的坐标；②根据题意可知，当0＜m＜时，点D′未到直线OC上，利用三角形面积公式可得出本题结果；③分情况讨论，分别求出当0＜m＜时，当＜m＜5时，当5＜m＜10时，当10＜m＜15时，S与m的关系式，分别令S＝，建立方程，求出m即可．【解答】解：（1）将点B（0，9），C（8，3）的坐标代入直线y＝kx+b，∴，解得．∴直线AB的函数表达式为：y＝﹣x+9；（2）①由（1）知直线AB的函数表达式为：y＝﹣x+9，令y＝0，则x＝12，∴A（12，0），∴OA＝12，OB＝9，∴AB＝15；如图1，过点C作CF⊥C′D′于点F，∴CF∥OA，∴∠OAB＝∠FCC′，∵∠C′FC＝∠BOA＝90°，∴△CFC′∽△AOB，∴OB：OA：AB＝C′F：CF：CC′＝9：12：15，∵CC′＝m，∴CF＝m，C′F＝m，∴C′（8﹣m，3+m），A′（12﹣m，m），D′（8﹣m，m），∵C（8，3），∴直线OC的解析式为：y＝x，∴E（8﹣m，3﹣m）.∴C′E＝3+m﹣（3﹣m）＝m．故答案为：m．②法一、当点D′落在直线OC上时，有m＝（8﹣m），解得m＝，∴当0＜m＜时，点D′未到直线OC，此时S＝C′E•CF＝•m•m＝m2；法二、∵C′D′∥BO，∴△CC′E∽△CBO，∴＝（）2，即＝，∴S＝m2．故答案为：m2．③法一、分情况讨论，当0＜m＜时，由②可知，S＝m2；令S＝m2＝，解得m＝＞（舍）或m＝﹣（舍）；当≤m＜5时，如图2，设线段A′D′与直线OC交于点M，∴M（m，m），∴D′E＝m﹣（3﹣m）＝m﹣3，D′M＝m﹣（8﹣m）＝m﹣8；∴S＝m2﹣•（m﹣3）•（m﹣8）＝﹣m2+m﹣12，令﹣m2+m﹣12＝；整理得，3m2﹣30m+70＝0，解得m＝或m＝＞5（舍）；当5≤m＜10时，如图3，S＝S△A′C′D′＝×4×3＝6≠，不符合题意；当10≤m≤15时，如图4，此时A′B＝15﹣m，∴BN＝（15﹣m），A′N＝（15﹣m），∴S＝•（15﹣m）•（15﹣m）＝（15﹣m）2，令（15﹣m）2＝，解得m＝15+2＞15（舍）或m＝15﹣2．法二、分情况讨论，当0＜m＜时，由②可知，S＝m2；令S＝m2＝，解得m＝＞（舍）或m＝﹣（舍）；（同法一）当≤m＜5时，如图2，设线段A′D′与直线OC交于点M，∵S△A′C′D′＝×4×3＝6，∴S△A′CM＝6﹣＝，∵S△AOC＝18，∵A′D′∥OA，∴△A′CM∽△ACO，∴＝，∴CA′＝，∴m＝C′A′﹣CA′＝5﹣，当5≤m＜10时，如图3，S＝S△A′C′D′＝×4×3＝6≠，不符合题意；当10≤m≤15时，如图4，∵A′D′∥x轴，∴△A′BK∽△ABO，∵S＝，S△ABO＝54，∴＝，解得BA′＝2，∴m＝BA﹣BA′＝15﹣2．故答案为：或15﹣2．【点评】本题属于一次函数综合题，涉及待定系数法求函数解析式，三角形的面积，相似三角形的性质与判定，分类讨论思想等知识，根据△A′C′D′的运动，进行正确的分类讨论是解题关键．考点四、反比例函数反比例函数中反比例系数的几何意义，如下图，过反比例函数图像上任一点作x轴、y轴的垂线PM，PN，垂足为M、N，则所得的矩形PMON的面积S=PM PN=.∴.典例4：（2022•东营）如图，一次函数y1＝k1x+b与反比例函数y2＝的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为﹣1，则不等式k1x+b＜的解集是（ ）A．﹣1＜x＜0或x＞2B．x＜﹣1或0＜x＜2C．x＜﹣1或x＞2D．﹣1＜x＜2【分析】根据两函数图象的上下位置关系结合交点横坐标，即可得出不等式k1x+b＜的解集，此题得解．【解答】解：观察函数图象可知，当﹣1＜x＜0或x＞2时，一次函数y1＝k1x+b的图象在反比例函数y2＝的图象的下方，∴不等式k1x+b＜的解集为：﹣1＜x＜0或x＞2，故选：A．【点评】本题考查了反比例函数与一次函数的交点问题，根据两函数图象的上下位置关系找出不等式的解集是解题的关键．典例5:（2022•徐州）如图，一次函数y＝kx+b（k＞0）的图象与反比例函数y＝（x＞0）的图象交于点A，与x轴交于点B，与y轴交于点C，AD⊥x轴于点D，CB＝CD，点C关于直线AD的对称点为点E．（1）点E是否在这个反比例函数的图象上？请说明理由；（2）连接AE、DE，若四边形ACDE为正方形．①求k、b的值；②若点P在y轴上，当|PE﹣PB|最大时，求点P的坐标．【分析】（1）设点A的坐标为（m，），根据轴对称的性质得到AD⊥CE，AD平分CE，如图，连接CE交AD于H，得到CH＝EH，求得E（2m，），于是得到点E在这个反比例函数的图象上；（2）①根据正方形的性质得到AD＝CE，AD垂直平分CE，求得CH＝AD，设点A的坐标为（m，），得到m＝2（负值舍去），求得A（2，4），C（0，2），把A（2，4），C（0，2）代入y＝kx+b得，解方程组即可得到结论；②延长ED交y轴于P，根据已知条件得到点B与点D关于y轴对称，求得|PE﹣PD|＝|PE﹣PB|，则点P 即为符合条件的点，求得直线DE的解析式为y＝x﹣2，于是得到结论．【解答】解：（1）点E在这个反比例函数的图象上，理由：∵一次函数y＝kx+b（k＞0）的图象与反比例函数y＝（x＞0）的图象交于点A，∴设点A的坐标为（m，），∵点C关于直线AD的对称点为点E，∴AD⊥CE，AD平分CE，如图．连接CE交AD于H，∴CH＝EH，∵BC＝CD，OC⊥BD，∴OB＝OD，∴OC＝AD，∵AD⊥x轴于D，∴CE∥x轴，∴E（2m，），∵2m×＝8，∴点E在这个反比例函数的图象上；（2）①∵四边形ACDE为正方形，∴AD＝CE，AD垂直平分CE，∴CH＝AD，设点A的坐标为（m，），∴CH＝m，AD＝，∴m＝×，∴m＝2（负值舍去），∴A（2，4），C（0，2），把A（2，4），C（0，2）代入y＝kx+b得，∴；②延长ED交y轴于P，∵CB＝CD，OC⊥BD，∴点B与点D关于y轴对称，∴|PE﹣PD|＝|PE﹣PB|，则点P即为符合条件的点，由①知，A（2，4），C（0，2），∴D（2，0），E（4，2），设直线DE的解析式为y＝ax+n，∴，∴，∴直线DE的解析式为y＝x﹣2，当x＝0时，y＝﹣2，∴P（0，﹣2）．故当|PE﹣PB|最大时，点P的坐标为（0，﹣2）．【点评】本题考查了反比例函数的综合题，正方形的性质，轴对称的性质，待定系数法求一次函数的解析式，正确地作出辅助线是解题的关键．考点五、二次函数1、两点间距离公式（当遇到没有思路的问题时，可用此方法拓展思路，以寻求解题方法）如图：点A坐标为（x1，y1），点B坐标为（x2，y2），则AB间的距离，即线段AB的长度为.2、函数平移规律：左加右减、上加下减.3、二次函数的最值如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当时，，当时，；如果在此范围内，y随x的增大而减小，则当时，，当时，.4、抛物线的对称变换①关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是.②关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是.③关于原点对称关于原点对称后，得到的解析式是；关于原点对称后，得到的解析式是.④关于顶点对称关于顶点对称后，得到的解析式是；关于顶点对称后，得到的解析式是．⑤关于点对称关于点对称后，得到的解析式是.根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此永远不变．求抛物线的对称图象的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．典例6:（2022•内蒙古）如图，抛物线y＝ax2+bx+c（a≠0）与x轴的一个交点坐标为（﹣1，0），抛物线的对称轴为直线x＝1，下列结论：①abc＜0；②3a+c＝0；③当y＞0时，x的取值范围是﹣1≤x＜3；④点（﹣2，y1），（2，y2）都在抛物线上，则有y1＜0＜y2.其中结论正确的个数是（ ）A．1个B．2个C．3个D．4个【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【解答】解：根据函数的对称性，抛物线与x轴的另外一个交点的坐标为（3，0）；①函数对称轴在y轴右侧，则ab＜0，而c＝3＞0，故abc＜0，故①正确，符合题意；②∵x＝﹣＝1，即b＝﹣2a，而x＝﹣1时，y＝0，即a﹣b+c＝0，∴a+2a+c＝0，∴3a+c＝0．∴②正确，符合题意；③由图象知，当y＞0时，x的取值范围是﹣1＜x＜3，∴③错误，不符合题意；④从图象看，当x＝﹣2时，y1＜0，当x＝2时，y2＞0，∴有y1＜0＜y2，故④正确，符合题意；故选：C．【点评】本题考查了二次函数图象与系数的关系：对于二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b 和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．考点六、函数的应用分段函数是指自变量在不同的取值范围内，其关系式（或图象）也不同的函数，分段函数的应用题多设计成两种情况以上，解答时需分段讨论.在现实生活中存在着很多需分段计费的实际问题，因此，分段计算的应用题成了近几年中考应用题的一种重要题型.典例7：（2022•德州）如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少一个条件而无法解答，经查询结果发现，该二次函数的解析式为y＝x2﹣4x+1．已知二次函数y＝ax2+bx+c的图象经过点A（0，1），B（1，﹣2），．求该二次函数的解析式．（1）请根据已有信息添加一个适当的条件：　C（2，﹣3）（答案不唯一）　；（2）当函数值y＜6时，自变量x的取值范围：　﹣1＜x＜5　；（3）如图1，将函数y＝x2﹣4x+1（x＜0）的图象向右平移4个单位长度，与y＝x2﹣4x+1（x≥4）的图象组成一个新的函数图象，记为L．若点P（3，m）在L上，求m的值；（4）如图2，在（3）的条件下，点A的坐标为（2，0），在L上是否存在点Q，使得S△OAQ＝9．若存在，求出所有满足条件的点Q的坐标；若不存在，请说明理由．【分析】（1）只需填一个在抛物线图象上的点的坐标即可；（2）求出y＝6时，对应的x值，再结合图象写出x的取值范围即可；（3）求出抛物线向右平移4个单位后的解析式为y＝（x﹣6）2﹣3，根据题意可知x＝3时，P点在抛物线y＝（x﹣6）2﹣3的部分上，再求m的值即可；（4）分两种情况讨论：当Q点在抛物线y＝（x﹣6）2﹣3的部分上时，设Q（t，t2﹣12x+33），由S△OAQ＝2×（t2﹣12x+33）＝9，求出Q点坐标即可；当Q点在抛物线y＝x2﹣4x+1的部分上时，设Q （m，m2﹣4m+1），由S△OAQ＝2×（m2﹣4m+1）＝9，求出Q点坐标即可．【解答】解：（1）C（2，﹣3），故答案为：C（2，﹣3）（答案不唯一）；（2）∵y＝x2﹣4x+1，∴当x2﹣4x+1＝6时，解得x＝5或x＝﹣1，∴当y＜6时，﹣1＜x＜5，故答案为：﹣1＜x＜5；（3）∵y＝x2﹣4x+1＝（x﹣2）2﹣3，∴抛物线向右平移4个单位后的解析式为y＝（x﹣6）2﹣3，当x＝3时，点P在抛物线y＝（x﹣6）2﹣3的部分上，∴m＝6；（4）存在点Q，使得S△OAQ＝9，理由如下：当Q点在抛物线y＝（x﹣6）2﹣3的部分上时，设Q（t，t2﹣12x+33），∴S△OAQ＝2×（t2﹣12x+33）＝9，解得t＝6+2或t＝6﹣2，∴t＜4，∴t＝6﹣2，∴Q（6﹣2，9）；当Q点在抛物线y＝x2﹣4x+1的部分上时，设Q（m，m2﹣4m+1），∴S△OAQ＝2×（m2﹣4m+1）＝9，解得m＝2+2或m＝﹣2，∵m≥4，∴m＝2+2，∴Q（2+2，9）；综上所述：Q点坐标为（6﹣2，9）或（2+2，9）．【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，函数图象平移的性质，数形结合解题是关键．。

八年级上册函数图像知识点在学习数学中，函数图像是一个重要的概念。

当我们学习函数图像时，需要明确一些关键的知识点。

下面将重点介绍八年级上册函数图像的知识点。

一、什么是函数图像？函数图像指数学中函数的图形，是指在平面直角坐标系中，通过将自变量的所有可能取值对应的因变量的值点进行连线而得到的连续曲线或曲线段的总称。

二、函数图像的表示方式当我们绘制函数图像时，可以选择不同的表示方式。

以下列举了常用的函数图像表示方式：1. 解析式函数的解析式是用一组公式来表示函数的数学表达式。

以y=f(x) 为例，通过将 x 带入函数中计算，得出对应的 y 值。

再将所有的 (x,y) 坐标点绘制在坐标系上，就形成了函数的图像。

2. 参数式函数的参数式是指将自变量 x 的值与一个或多个参数符号 t 进行关联。

通过改变参数 t 的取值，使函数的图像发生变化。

以y=at+b 为例，通过改变 a 和 b 的取值，可以绘制出不同的直线图像。

3. 点列式点列式将函数对应的坐标点逐一列出，然后将这些点进行连线，即可得到该函数的图像。

点列式的表达方式直接清晰，适合于人工绘图或计算机绘图。

三、常见函数图像1. 一次函数一次函数又称为一元一次函数，是指函数的最高次项为一次的函数。

一次函数的图像为一条直线，具有一定的倾斜度。

2. 二次函数二次函数又称为一元二次函数，是指函数的最高次项为二次的函数。

二次函数的图像为一条开口向上或开口向下的 U 型曲线。

3. 立方函数立方函数的最高次项为三次，是一种平滑的连续曲线。

立方函数的图像为一条先向负无穷走，再向正无穷走的 S 型曲线。

4. 指数函数指数函数是一个以常数 e 为底的幂函数，具有固定的单调性和对称轴。

指数函数的图像为一条向上凸起的曲线。

5. 对数函数对数函数的图像为一条斜率逐渐减小趋向于零的曲线。

四、绘制函数图像的方法1. 通过解析式绘制函数图像根据函数的解析式，计算 x 取不同的值对应的 y 值，然后将这些坐标点绘制在坐标系中，即可得到函数的图像。

冲刺中考数学压轴之满分集训专题02函数图像与性质综合题（四大类）【类型一：分析函数图像】【典例1】（锦州）已知A，B两地相距10千米，上午9：00甲骑电动车从A 地出发到B地，9：10乙开车从B地出发到A地，甲、乙两人距A地的距离y（千米）与甲所用的时间x（分）之间的关系如图所示，则乙到达A地的时间为．【答案】9：20【解答】解：因为甲30分走完全程10千米，所以甲的速度是千米/分，由图中看出两人在走了5千米时相遇，那么甲此时用了15分钟，则乙用了（15﹣10）分钟，所以乙的速度为：5÷5＝1千米/分，所以乙走完全程需要时间为：10÷1＝10分，因为9：10乙才出发，所以乙到达A地的时间为9：20；故答案为9：20．【变式1-1】（2022•潍坊）如图，在▱ABCD中，∠A＝60°，AB＝2，AD＝1，点E，F在▱ABCD的边上，从点A同时出发，分别沿A→B→C和A→D→C 的方向以每秒1个单位长度的速度运动，到达点C时停止，线段EF扫过区域的面积记为y，运动时间记为x，能大致反映y与x之间函数关系的图象是（）A．B．C．D．【答案】A【解答】解：过点F作FH⊥AB于H，当0≤x≤1时，如图1，在Rt△FAH中，AF＝x，∠A＝60°，则FH＝AF•sin A＝x，∴线段EF扫过区域的面积y＝x•x＝x2，图象是开口向上的抛物线，当1＜x≤2时，如图2，过点D作DP⊥AB于P，则DP＝AD•sin A＝，∴线段EF扫过区域的面积y＝×（x﹣1+x）×＝x﹣，图象是y 随x的增大而增大的线段，当2＜x≤3时，如图3，过点E作EG⊥CD于G，则CE＝CF＝3﹣x，∴EG＝（3﹣x），∴线段EF扫过区域的面积y＝2×﹣×（3﹣x）×（3﹣x）＝﹣（3﹣x）2，图象是开口向下的抛物线，故选：A．【变式1-2】（2022•齐齐哈尔）如图①所示（图中各角均为直角），动点P从点A出发，以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动，△AFP的面积y随点P运动的时间x（秒）之间的函数关系图象如图②所示，下列说法正确的是（）A．AF＝5B．AB＝4C．DE＝3D．EF＝8【答案】B【解答】解：由图②的第一段折线可知：点P经过4秒到达点B处，此时的三角形的面积为12，∵动点P从点A出发，以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动，∴AB＝4．∵×AF•AB＝12，∴AF＝6，∴A选项不正确，B选项正确；由图②的第二段折线可知：点P再经过2秒到达点C处，∴BC＝2，由图②的第三段折线可知：点P再经过6秒到达点D处，∴CD＝6，由图②的第四段折线可知：点P再经过4秒到达点E处，∴DE＝4．∴C选项不正确；∵图①中各角均为直角，∴EF＝AB+CD＝4+6＝10，∴D选项的结论不正确，故选：B．【变式1-3】（2022•宜昌）如图是小强散步过程中所走的路程s（单位：m）与步行时间t（单位：min）的函数图象．其中有一时间段小强是匀速步行的．则这一时间段小强的步行速度为（）A．50m/min B．40m/min C．m/min D．20m/min【答案】D【解答】解：由函数图象知，从30﹣70分钟时间段小强匀速步行，∴这一时间段小强的步行速度为＝20（m/min），故选：D．【变式1-4】（2022•辽宁）如图，在等边三角形ABC中，BC＝4，在Rt△DEF 中，∠EDF＝90°，∠F＝30°，DE＝4，点B，C，D，E在一条直线上，点C，D重合，△ABC沿射线DE方向运动，当点B与点E重合时停止运动．设△ABC运动的路程为x，△ABC与Rt△DEF重叠部分的面积为S，则能反映S与x之间函数关系的图象是（）A．B．C．D．【答案】A【解答】解：过点A作AM⊥BC，交BC于点M，在等边△ABC中，∠ACB＝60°，在Rt△DEF中，∠F＝30°，∴∠FED＝60°，∴∠ACB＝∠FED，∴AC∥EF，在等边△ABC中，AM⊥BC，∴BM＝CM＝BC＝2，AM＝BM＝2，＝BC•AM＝4，∴S△ABC①当0＜x≤2时，设AC与DF交于点G，此时△ABC与Rt△DEF重叠部分为△CDG，由题意可得CD＝x，DG＝x∴S＝CD•DG＝x2；②当2＜x≤4时，设AB与DF交于点G，此时△ABC与Rt△DEF重叠部分为四边形AGDC，由题意可得：CD＝x，则BD＝4﹣x，DG＝（4﹣x），﹣S△BDG＝4﹣×（4﹣x）×（4﹣x），∴S＝S△ABC∴S＝﹣x2+4x﹣4＝﹣（x﹣4）2+4，③当4＜x≤8时，设AB与EF交于点G，过点G作GM⊥BC，交BC于点M，此时△ABC与Rt△DEF重叠部分为△BEG，由题意可得CD＝x，则CE＝x﹣4，DB＝x﹣4，∴BE＝x﹣（x﹣4）﹣（x﹣4）＝8﹣x，∴BM＝4﹣x在Rt△BGM中，GM＝（4﹣x），∴S＝BE•GM＝（8﹣x）×（4﹣x），∴S＝（x﹣8）2，综上，选项A的图像符合题意，故选：A．【类型二：判断函数图像】【典例2】（2020•铜仁市）如图，在矩形ABCD中，AB＝3，BC＝4，动点P沿折线BCD从点B开始运动到点D，设点P运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（）A．B．C．D．【答案】D【解答】解：由题意当0≤x≤4时，y＝×AD×AB＝×3×4＝6，当4＜x＜7时，y＝×PD×AD＝×（7﹣x）×4＝14﹣2x．故选：D．【变式2-1】（2022•湖北）如图，边长分别为1和2的两个正方形，其中有一条边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形的面积为S1，小正方形与大正方形重叠部分的面积为S2，若S＝S1﹣S2，则S随t变化的函数图象大致为（）A．B．C．D．【答案】A【解答】解：由题意得：当0≤t＜1时，S＝4﹣t，当1≤t≤2时，S＝3，当2＜＜t≤3时，S＝t+1，故选：A．【变式2-2】（2022•绥化）已知二次函数y＝ax2+bx+c的部分函数图象如图所示，则一次函数y＝ax+b2﹣4ac与反比例函数y＝在同一平面直角坐标系中的图象大致是（）A．B．C．D．【答案】B【解答】解：∵二次函数y＝ax2+bx+c的部分函数图象开口向上，∴a＞0，∵二次函数y＝ax2+bx+c的部分函数图象顶点在x轴下方，开口向上，∴二次函数y＝ax2+bx+c的图象与x轴有两个交点，b2﹣4ac＞0，∴一次函数y＝ax+b2﹣4ac的图象位于第一，二，三象限，由二次函数y＝ax2+bx+c的部分函数图象可知，点（2，4a+2b+c）在x轴上方，∴4a+2b+c＞0，∴y＝的图象位于第一，三象限，据此可知，符合题意的是B，故选：B．【变式2-3】（2022•广西）已知反比例函数y＝（b≠0）的图象如图所示，则一次函数y＝cx﹣a（c≠0）和二次函数y＝ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．【答案】D【解答】解：∵反比例函数y＝（b≠0）的图象位于一、三象限，∴b＞0；∵A、B的抛物线都是开口向下，∴a＜0，根据同左异右，对称轴应该在y轴的右侧，故A、B都是错误的．∵C、D的抛物线都是开口向上，∴a＞0，根据同左异右，对称轴应该在y轴的左侧，∵抛物线与y轴交于负半轴，∴c＜0由a＞0，c＜0，排除C．故选：D．【类型三：反比例函数综合】【典例3】（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36B．18C．12D．9【答案】B【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图象上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B【变式3-1】（2021•鄂州）如图，点A是反比例函数y＝（x＞0）的图象上一点，过点A作AC⊥x轴于点C，AC交反比例函数y＝（x＞0）的图象于点B，点P是y轴正半轴上一点．若△PAB的面积为2，则k的值为．【答案】8【解答】解：连接OA、OB，∵AC⊥x轴，∴AC∥y轴，＝S△APB，∴S△AOB＝2，∵S△APB＝2，∴S△AOB由反比例函数系数k的几何意义可得：S△AOC＝6，S△BOC＝，∴6﹣＝2，解得：k＝8，故答案为8．【变式3-2】（2021•荆州）如图，过反比例函数y＝（k＞0，x＞0）图象上的四点P1，P2，P3，P4分别作x轴的垂线，垂足分别为A1，A2，A3，A4，再过P1，P2，P3，P4分别作y轴，P1A1，P2A2，P3A3的垂线，构造了四个相邻的矩形．若这四个矩形的面积从左到右依次为S1，S2，S3，S4，OA1＝A1A2＝A2A3＝A3A4，则S1与S4的数量关系为．【答案】S1＝4S4【解答】解：∵过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积S 是个定值，OA1＝A1A2＝A2A3＝A3A4，∴S1＝k，S2＝k，S3＝k，S4＝k，∴S1＝4S4．故答案为：S1＝4S4．【变式3-3】（2022•毕节市）如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y＝（x＞0，k＞0）的图象经过点C，E．若点A（3，0），则k的值是．【答案】4【解答】解：设C（m，），∵四边形ABCD是正方形，∴点E为AC的中点，∴E（，），∵点E在反比例函数y＝上，∴，∴m＝1，作CH⊥y轴于H，∴CH＝1，∵四边形ABCD是正方形，∴BA＝BC，∠ABC＝90°，∴∠OBA＝∠HCB，∵∠AOB＝∠BHC，∴△AOB≌△BHC（AAS），∴BH＝OA＝3，OB＝CH＝1，∴C（1，4），∴k＝4，故答案为：4．【变式3-4】（2022•雁塔区校级模拟）如图，正方形ACBE的边长是，点B，C分别在x轴和y轴正半轴上，BO＝2，ED⊥x轴于点D，ED的中点F在反比例函数y＝（x＞0）的图象上，则k＝．【答案】3【解答】解：∵正方形ACBE的边长是，BO＝2，∴BC＝BE＝，∴OC＝＝＝1，∵∠ABC＝90°，∴∠OBC+∠EBD＝90°，∵∠OBC+∠OCB＝90°，∴∠OCB＝∠EBD，在△OBC和△DEB中，，∴△OBC≌△DEB（AAS），∴BD＝OC＝1，DE＝OB＝2，∴OD＝3，∴E（3，2），∵点F是ED的中点，∴F（3，1），∵点F在反比例函数y＝（x＞0）的图象上，∴k＝3×1＝3，故答案为3．【变式3-5】（2021•广元）如图，点A（﹣2，2）在反比例函数y＝的图象上，点M在x轴的正半轴上，点N在y轴的负半轴上，且OM＝ON＝5．点P（x，y）是线段MN上一动点，过点A和P分别作x轴的垂线，垂足为点D和E，＜S△OPE时，x的取值范围是．连接OA、OP．当S△OAD【答案】1＜x＜4【解答】解：过点B作BF⊥ON于F，连接OB，过点C作CG⊥OM于点G，连接OC，如图，∵点A（﹣2，2）在反比例函数y＝的图象上，∴k＝﹣4．∴y＝．∵点A（﹣2，2），∴AD＝OD＝2．∴．设B（a，b），则ab＝﹣4，OF＝﹣b，BF＝a．∴＝＝2．＝2．同理：S△OCG＞S△OBF，从图中可以看出当点P在线段BC上时，S△OPE＜S△OPE．即当点P在线段BC上时，满足S△OAD∵OM＝ON＝5，∴N（0，﹣5），M（5，0）．设直线MN的解析式为y＝mx+n，则：，解得：．∴直线MN的解析式为y＝x﹣5．∴，解得：，．∴B（1，﹣4），C（4，﹣1）．∴x的取值范围为1＜x＜4．【变式3-6】（2021•荆门）如图，在平面直角坐标系中，Rt△OAB斜边上的高为1，∠AOB＝30°，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A的对应点C恰好在函数y＝（k≠0）的图象上，若在y＝的图象上另有一点M使得∠MOC＝30°，则点M的坐标为．【答案】（，1）【解答】解：作AE⊥OB于E，MF⊥x轴于F，则AE＝1，∵∠AOB＝30°，∴OE＝AE＝，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A的对应点C为（1，），∵点C在函数y＝（k≠0）的图象上，∴k＝1×＝，∴y＝，∵∠COD＝∠AOB＝30°，∠MOC＝30°，∴∠DOM＝60°，∴∠MOF＝30°，∴OF＝MF，设MF＝n，则OF＝n，∴M（n，n），∵点M在函数y＝的图象上，∴n＝，∴n＝1（负数舍去），∴M（，1），故答案为（，1）．【变式3-7】（2021•达州）如图，将一把矩形直尺ABCD和一块等腰直角三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，EF交BC于点M，反比例函数y＝（x＜0）的图象恰好经过点F，M，若直尺的宽CD＝1，三角板的斜边FG＝4，则k＝．【答案】﹣12【解答】解：过点M作MN⊥AD，垂足为N，则MN＝CD＝1，在Rt△FMN中，∠MFN＝45°，∴FN＝MN＝1又∵FG＝4，∴NA＝MB＝FG﹣FN＝4﹣1＝3，设OA＝a，则OB＝a+1，∴点F（﹣a，4），M（﹣a﹣1，3），又∵反比例函数y＝（x＜0）的图象恰好经过点F，M，∴k＝﹣4a＝3（﹣a﹣1），解得，a＝3，∴k＝﹣4a＝﹣12，故答案为：﹣12．【类型4：二次函数综合】【典例4】（2021•广安）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0，②4a﹣2b+c＜0，③a﹣b≥x（ax+b），④3a+c＜0，正确的有（）A．1个B．2个C．3个D．4个【答案】C【解答】解：∵抛物线开口向下，∴a＜0，∵对称轴为直线x＝﹣1，即，∴b＝2a，则b＜0，∵抛物线与y轴交于正半轴，∴c＞0，∴abc＞0，故①正确；∵抛物线对称轴为直线x＝﹣1，与x轴的一个交点横坐标在0和1之间，则与x轴的另一个交点在﹣2和﹣3之间，∴当x＝﹣2时，y＝4a﹣2b+c＞0，故②错误；∵x＝﹣1时，y＝ax2+bx+c的最大值是a﹣b+c，∴a﹣b+c≥ax2+bx+c，∴a﹣b≥ax2+bx，即a﹣b≥x（ax+b），故③正确；∵当x＝1时，y＝a+b+c＜0，b＝2a，∴a+2a+c＝3a+c＜0，故④正确；故选：C．【变式4-1】（2022•辽宁）抛物线y＝ax2+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，直线y＝kx+c与抛物线都经过点（﹣3，0）．下列说法：①ab＞0；②4a+c＞0；③若（﹣2，y1）与（，y2）是抛物线上的两个点，则y1＜y2；④方程ax2+bx+c＝0的两根为x1＝﹣3，x2＝1；⑤当x＝﹣1时，函数y＝ax2+（b﹣k）x有最大值．其中正确的个数是（）A．2B．3C．4D．5【答案】A【解答】解：∵抛物线的开口方向向下，∴a＜0．∵抛物线的对称轴为直线x＝﹣1，∴﹣＝﹣1，∴b＝2a，b＜0．∵a＜0，b＜0，∴ab＞0，∴①的结论正确；∵抛物线y＝ax2+bx+c经过点（﹣3，0），∴9a﹣3b+c＝0，∴9a﹣3×2a+c＝0，∴3a+c＝0．∴4a+c＝a＜0，∴②的结论不正确；∵抛物线的对称轴为直线x＝﹣1，∴点（﹣2，y1）关于直线x＝﹣1对称的对称点为（0，y1），∵a＜0，∴当x＞﹣1时，y随x的增大而减小．∵＞0＞﹣1，∴y1＞y2．∴③的结论不正确；∵抛物线的对称轴为直线x＝﹣1，抛物线经过点（﹣3，0），∴抛物线一定经过点（1，0），∴抛物线y＝ax2+bx+c与x轴的交点的横坐标为﹣3，1，∴方程ax2+bx+c＝0的两根为x1＝﹣3，x2＝1，∴④的结论正确；∵直线y＝kx+c经过点（﹣3，0），∴﹣3k+c＝0，∴c＝3k．∵3a+c＝0，∴c＝﹣3a，∴3k＝﹣3a，∴k＝﹣a．∴函数y＝ax2+（b﹣k）x＝ax2+（2a+a）x＝ax2+3ax＝a﹣a，∵a＜0，∴当x＝﹣时，函数y＝ax2+（b﹣k）x有最大值，∴⑤的结论不正确．综上，结论正确的有：①④，故选：A．【变式4-2】（2022•烟台）二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，其对称轴为直线x＝﹣，且与x轴的一个交点坐标为（﹣2，0）．下列结论：①abc＞0；②a＝b；③2a+c＝0；④关于x的一元二次方程ax2+bx+c﹣1＝0有两个相等的实数根．其中正确结论的序号是（）A．①③B．②④C．③④D．②③【答案】D【解答】解：①由图可知：a＞0，c＜0，＜0，∴b＞0，∴abc＜0，故①不符合题意．②由题意可知：＝﹣，∴b＝a，故②符合题意．③将（﹣2，0）代入y＝ax2+bx+c，∴4a﹣2b+c＝0，∵a＝b，∴2a+c＝0，故③符合题意．④由图象可知：二次函数y＝ax2+bx+c的最小值小于0，令y＝1代入y＝ax2+bx+c，∴ax2+bx+c＝1有两个不相同的解，故④不符合题意．故选：D．【变式4-3】（2022•梧州）如图，已知抛物线y＝ax2+bx﹣2的对称轴是直线x ＝﹣1，直线l∥x轴，且交抛物线于点P（x1，y1），Q（x2，y2），下列结论错误的是（）A．b2＞﹣8aB．若实数m≠﹣1，则a﹣b＜am2+bmC．3a﹣2＞0D．当y＞﹣2时，x1•x2＜0【答案】C【解答】解：根据函数图象可知a＞0，根据抛物线的对称轴公式可得x＝﹣＝﹣1，∴b＝2a，∴b2＞0，﹣8a＜0，∴b2＞﹣8a．故A正确，不符合题意；∵函数的最小值在x＝﹣1处取到，∴若实数m≠﹣1，则a﹣b﹣2＜am2+bm﹣2，即若实数m≠﹣1，则a﹣b＜am2+bm．故B正确，不符合题意；∵l∥x轴，∴y1＝y2，令x＝0，则y＝﹣2，即抛物线与y轴交于点（0，﹣2），∴当y1＝y2＞﹣2时，x1＜0，x2＞0．∴当y1＝y2＞﹣2时，x1•x2＜0．故D正确，不符合题意；∵a＞0，∴3a＞0，没有条件可以证明3a＞2．故C错误，符合题意；故选：C．【变式4-4】（2022•天津）已知抛物线y＝ax2+bx+c（a，b，c是常数，0＜a＜c）经过点（1，0），有下列结论：①2a+b＜0；②当x＞1时，y随x的增大而增大；③关于x的方程ax2+bx+（b+c）＝0有两个不相等的实数根．其中，正确结论的个数是（）A．0B．1C．2D．3【答案】C【解答】解：①∵抛物线y＝ax2+bx+c经过点（1，0），∴a+b+c＝0，∵a＜c，∴a+b+a＜0，即2a+b＜0，本小题结论正确；②∵a+b+c＝0，0＜a＜c，∴b＜0，∴对称轴x＝﹣＞1，∴当1＜x＜﹣时，y随x的增大而减小，本小题结论错误；③∵a+b+c＝0，∴b+c＝﹣a，对于方程ax2+bx+（b+c）＝0，Δ＝b2﹣4×a×（b+c）＝b2+4a2＞0，∴方程ax2+bx+（b+c）＝0有两个不相等的实数根，本小题结论正确；故选：C．【变式4-5】（2021•福建）二次函数y＝ax2﹣2ax+c（a＞0）的图象过A（﹣3，y1），B（﹣1，y2），C（2，y3），D（4，y4）四个点，下列说法一定正确的是（）A．若y1y2＞0，则y3y4＞0B．若y1y4＞0，则y2y3＞0C．若y2y4＜0，则y1y3＜0D．若y3y4＜0，则y1y2＜0【答案】C【解答】解：如图，由题意对称轴为直线x＝1，观察图象可知，y1＞y4＞y2＞y3，若y1y2＞0，如图1中，则y3y4＜0，选项A不符合题意，若y1y4＞0，如图2中，则y2y3＜0，选项B不符合题意，若y2y4＜0，如图3中，则y1y3＜0，选项C符合题意，若y3y4＜0，如图4中，则y1y2＞0，选项D不符合题意，故选：C．【变式4-6】（2021•恩施州）如图，已知二次函数y＝ax2+bx+c的图象与x轴交于（﹣3，0），顶点是（﹣1，m），则以下结论：①abc＞0；②4a+2b+c＞0；③若y≥c，则x≤﹣2或x≥0；④b+c＝m．其中正确的有（）个．A．1B．2C．3D．4【答案】B【解答】解：①∵抛物线开口向上，对称轴在y轴左边，与y轴交于负半轴，∴a＞0，b＞0，c＜0，∴abc＜0，故结论①错误；②∵二次函数y＝ax2+bx+c的图象与x轴交于（﹣3，0），顶点是（﹣1，m），∴抛物线与x轴的另一个交点为（1，0），∵抛物线开口向上，∴当x＝2时，y＝4a+2b+c＞0，故结论②正确；③由题意可知对称轴为：直线x＝﹣1，∴x＝，∴b＝2a，把y＝c，b＝2a代入y＝ax2+bx+c得：ax2+2ax+c＝c，∴x2+2x＝0，解得x＝0或﹣2，∴当y≥c，则x≤﹣2或x≥0，故结论③正确；④把（﹣1，m），（1，0）代入y＝ax2+bx+c得：a﹣b+c＝m，a+b+c＝0，∴b＝，∵b＝2a，∴a＝，∵抛物线与x轴的另一个交点为（1，0），∴a+b+c＝0，∴c＝，∴b+c＝，故选：B．。

函数图像知识点在数学的世界里，函数图像就像是函数的“照片”，它以直观的方式展现了函数的性质和特点。

理解函数图像对于我们掌握函数的行为、解决相关问题以及深入理解数学的本质都具有极其重要的意义。

首先，我们来聊聊什么是函数图像。

简单来说，函数图像就是把函数中自变量和因变量的对应关系用图形的形式表现出来。

比如说，对于函数 y ＝ 2x ＋ 1，我们可以通过给 x 赋予不同的值，计算出相应的y 值，然后把这些（x, y) 的坐标点在平面直角坐标系中标记出来，再用平滑的线把它们连接起来，就得到了这个函数的图像。

函数图像的类型多种多样。

常见的有直线、抛物线、双曲线等等。

直线函数图像，就像我们刚才提到的 y ＝ 2x ＋ 1，它的图像是一条直线。

而抛物线函数图像，比如 y ＝ x²，它的形状就像一个开口朝上或朝下的“碗”。

双曲线函数图像，像 y ＝ 1/x，它的形状则有自己独特的特点。

在观察函数图像时，有几个关键的要素需要我们注意。

一个是定义域和值域。

定义域就是函数中自变量 x 能够取值的范围，而值域则是因变量 y 相应的取值范围。

从图像上来看，定义域就是图像在 x 轴上的覆盖范围，值域则是图像在 y 轴上的覆盖范围。

再说说单调性。

如果函数图像从左到右一直上升，那这个函数就是单调递增的；如果图像从左到右一直下降，那就是单调递减的。

比如说，对于函数 y ＝ x³，它在整个实数范围内都是单调递增的，从图像上就能清晰地看出来。

还有奇偶性。

如果函数图像关于y 轴对称，那这个函数就是偶函数；如果图像关于原点对称，那就是奇函数。

比如，y ＝ x²是偶函数，y ＝x³是奇函数。

通过观察图像的对称性，我们可以很容易地判断函数的奇偶性。

函数图像的平移也是一个重要的知识点。

比如说，对于函数 y ＝ x²，如果把它向左平移 2 个单位，就变成了 y ＝（x ＋ 2)²；如果向上平移3 个单位，就变成了 y ＝ x²＋ 3 。

五大基本函数图像及性质经过数学发展的几千年，函数成为数学研究的主要内容之一，用来描述理解宇宙规律的精妙抽象工具，而函数图像则是这些函数形式反射出来的表达形式。

在数学探索中，五种基本函数图像最为常见，它们分别是：直线函数图像，二次函数图像，指数函数图像，对数函数图像和正弦函数图像。

直线函数图像是函数图像中最简单的一种形式，它可以用方程的形式y=kx +b来表示，其中K表示斜率，b表示偏移量，x、y是函数的模型变量，模型变量是可以表达数学物理实验结果的变量。

斜率便是表示函数图像斜线斜率，偏移量是表示函数图像经过y轴的截距，而此类函数一般没有极限，但伴随着变量不断变化而无限的延伸。

这种特性使它成为很多具有统计推论意义的实验结果的基础数据，在解决微积分问题时也是非常重要的概念。

二次函数图像的基本形式为y=ax^2 +bx +c，其中a,b,c代表的是函数的方程的三个常数，x是函数模型变量，y是函数的值，在实际应用中，一般需要将该方程写成y=a(x-h)^2 +k的形式；a为非负实数，当a为0时，表示函数直线，当a不为0时，表示函数曲线；h是函数的极值点横坐标，k是函数极值点的点的纵坐标，这样的函数有两个极值点，极值点的大小取决于a的正负，正值表示极值点为最小值，负值表示极值点为最大值。

指数函数图像是根据指数函数进行描述的，其基本形式为y=a^x，其中a为正实数，x为函数模型变量，y为函数值，这种函数图像有两个极限，即横坐标上趋于无穷大时，纵坐标为正负无穷大，指数函数在应用时非常广泛，它可以用来描述多种不同的物理实验结果，比如温度变化，加速速度的变化等等。

对数函数图像是根据对数函数来描绘的，其基本形式为y=loga(x)，其中a是底数，x是函数模型变量，y是函数值，这种函数图像的横坐标上的极限为0，纵坐标上的极限为正负无穷大，对数函数可以用来描述指数函数和二次函数的变化，在温度变化，分子运动速度和其它变化等等应用也十分重要。

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线，其一般形式为 y = mx + b，其中 m是斜率，b 是 y 轴截距。

当 m > 0 时，直线向上倾斜；当 m < 0 时，直线向下倾斜。

2. 二次函数图像二次函数图像是一个抛物线，其一般形式为 y = ax^2 + bx + c，其中 a、b、c 是常数。

当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。

3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。

正弦函数图像是一条波动曲线，余弦函数图像与正弦函数图像相似，但相位差为π/2。

正切函数图像是一条周期性振荡的曲线。

4. 指数函数图像指数函数图像是一条上升或下降的曲线，其一般形式为 y = a^x，其中 a 是底数，x 是指数。

当 a > 1 时，曲线上升；当 0 < a < 1 时，曲线下降。

5. 对数函数图像对数函数图像是一条上升或下降的曲线，其一般形式为 y =log_a(x)，其中 a 是底数，x 是真数。

当 a > 1 时，曲线上升；当0 < a < 1 时，曲线下降。

6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。

双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线，而双曲正切函数图像是一条周期性振荡的曲线。

7. 幂函数图像幂函数图像是一条上升或下降的曲线，其一般形式为 y = x^n，其中 n 是指数。

当 n > 0 时，曲线上升；当 n < 0 时，曲线下降。

8. 反比例函数图像反比例函数图像是一条双曲线，其一般形式为 y = k/x，其中 k是常数。

当 k > 0 时，曲线位于第一和第三象限；当 k < 0 时，曲线位于第二和第四象限。

经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数，包括反正弦函数、反余弦函数和反正切函数。

八年级函数图像知识点函数图像是初中数学中一个非常重要的知识点，学好函数图像的知识不仅可以为学生将来学习高中数学和大学数学打下坚实的基础，而且还可以为学生成为优秀的一个数学家打下基础。

在这篇文章中，我将会涉及到八年级函数图像的几个重要知识点。

一、一次函数一次函数是最简单的线性函数，可以用y=kx+b 的方式来表达，其中 k 是斜率， b 是截距。

一次函数的图像是一条直线，斜率为正的直线向右上方倾斜，斜率为负的则向右下方倾斜。

当斜率k=0 时，直线是水平的；当 b=0 时，直线经过原点，称为原点通过的直线。

二、二次函数二次函数是常见的非线性函数之一，可以用 y=ax²+bx+c 的方式来表达，其中 a 不等于0。

a 的正负决定了二次函数开口朝上或朝下，当 a>0 时，二次函数开口朝上，当 a<0 时，二次函数开口朝下。

b 的正负决定了二次函数的对称轴位置，对称轴的方程为 x=-b/2a。

c 影响了二次函数的 y 坐标截距。

当 a=1，b=c=0 时，二次函数变为 y=x²，这是一个基础的二次函数，成为抛物线。

三、指数函数指数函数是 y=a^x 的函数形式，其中 a 是正数，且不等于 1。

当a>1 时，指数函数增长迅速；当0<a<1 时，指数函数衰减迅速。

指数函数的图像随着指数 x 不断增加而上升或下降，与 x 轴永不相交。

指数函数有一个特殊的基础函数 y=2^x，这个函数的图像是一条向上的曲线，与 x 轴相交于 x 轴上方的一点。

指数函数是一种常用的模型，可以描述很多实际现象，如细菌数量增长、放射性衰变等。

四、对数函数对数函数是 y=loga(x) 的函数形式，其中 a 是正数，不等于 1。

这个函数的反函数是指数函数。

当 a>1 时，对数函数单调增加，当 0<a<1 时，对数函数单调减少。

对数函数的图像有一个特殊点(1,0)，这是因为 loga(a^x)=x，所以当 x=0 时，a^x=1，对数函数得到最小值 0。

初中常见函数题型总结归纳函数作为数学的一个重要概念，在初中数学中占据着重要地位。

掌握函数的概念和常见题型对学生来说非常重要。

本文将对初中常见的函数题型进行总结和归纳，帮助学生更好地掌握函数的概念和解题方法。

一、线性函数题型1. 线性函数的定义和表示：线性函数是指函数的图像为一条直线的函数，常用的表示形式为f(x) = kx + b，其中k和b为常数。

2. 求解线性函数的截距：当已知函数的图像经过一点(x₀, y₀)时，可利用该点求解出函数的截距b。

通过代入(x₀, y₀)和f(x) = kx + b，解出b的值。

3. 求解线性函数的斜率：斜率k表示函数图像上每增加一个单位自变量x，函数值增加的量。

当已知函数的图像经过两点(x₁, y₁)和(x₂, y₂)时，斜率k可通过公式k = (y₂ - y₁) / (x₂ - x₁) 计算得出。

4. 求解线性函数与坐标轴的交点：函数与x轴的交点称为零点，与y轴的交点称为截距。

通过将x=0或y=0代入线性函数的表达式中，可以求出函数与坐标轴的交点。

二、二次函数题型1. 二次函数的定义和表示：二次函数是指函数的图像为抛物线的函数，常用的表示形式为f(x) = ax² + bx + c，其中a、b和c为常数，且a ≠ 0。

2. 求解二次函数的顶点：二次函数的顶点是抛物线的最高点或最低点，可以通过公式x = -b / (2a) 求解。

3. 求解二次函数与坐标轴的交点：通过将x=0或y=0代入二次函数的表达式中，可以求出函数与坐标轴的交点。

4. 二次函数图像的平移和翻转：二次函数图像可以通过平移和翻转实现形状的改变。

平移可以通过在函数表达式中引入常数h和k实现，使得f(x) = a(x-h)² + k。

翻转可以通过将函数表达式中的二次项的系数a取负值实现。

三、组合函数题型1. 组合函数的定义和表示：组合函数是指由两个函数嵌套而成的函数。

例如，给定函数f(x)和g(x)，则组合函数可以表示为h(x) = f(g(x))。

初中数学函数图像知识点汇总函数是数学中的重要概念，而函数图像则是理解函数性质的重要工具之一。

在初中数学中，学习函数图像有助于学生理解函数的变化规律、性质和应用。

下面将对初中数学函数图像的知识点进行详细总结。

1. 基本函数图像：(1) 常数函数 f(x)=a : 这是一条平行于x轴的直线，横坐标不变，纵坐标为常数a。

(2) 一次函数 f(x)=kx+b : 这是一条斜率为k的直线，纵截距为b。

(3) 平方函数 f(x)=x^2 : 这是一条开口向上的抛物线，对称轴是y轴。

(4) 绝对值函数 f(x)=|x| : 这是一条以原点为顶点的V字形折线。

2. 函数的变换：(1) 平移：将函数图像沿x轴或y轴平行地移动。

当函数图像向右平移h单位时，函数表示形式为f(x-h)；当函数图像向上平移k单位时，函数表示形式为f(x)+k。

(2) 翻折：将函数图像沿x轴或y轴翻转。

当函数图像关于x轴对称时，函数表示形式为-f(x)；当函数图像关于y轴对称时，函数表示形式为f(-x)。

(3) 压缩与拉伸：将函数图像沿x轴或y轴进行扩大或缩小。

当函数图像水平方向压缩为原来的1/a倍，纵轴方向拉伸为原来的a倍时，函数表示形式为f(ax)；当函数图像水平方向拉伸为原来的a倍，纵轴方向压缩为原来的1/a倍时，函数表示形式为f(x/a)。

3. 常见函数图像特征：(1) 斜率：一次函数的斜率代表了函数图像的倾斜程度。

斜率越大，函数图像越陡峭。

(2) 零点：函数图像与x轴相交的点称为零点。

零点对应于函数的解，即f(x)=0。

(3) 最值：函数图像的最高点称为最大值，最低点称为最小值。

(4) 对称中心：若函数图像关于某一点对称，则该点为对称中心。

常见对称中心有原点和y轴。

(5) 单调性：函数图像在某一区间上递增或递减称为函数的单调性。

4. 常用函数图像的特点：(1) 常数函数 f(x)=a : 函数图像平行于x轴，斜率为0，没有零点，单调性为常数。

函数的图像一、必备知识：1．作函数的图象有两种基本方法：(1)利用描点法作图，其一般步骤为：①确定函数定义域；②化简函数解析式；③讨论函数的性质(奇偶性、单调性、周期性、最值等)；④描点并作出函数图象．(2)图象变换法．2．图象变换的四种形式(1)平移变换①水平平移：y＝f(x)的图象向左平移a(a＞0)个单位长度，得到________的图象；y＝f(x－a)(a＞0)的图象可由y＝f(x)的图象向________平移a个单位长度而得到．②竖直平移：y＝f(x)的图象向上平移b(b＞0)个单位长度，得到________的图象；y＝f(x)－b(b＞0)的图象可由y＝f(x)的图象向________平移b个单位长度而得到．总之，对于平移变换，记忆口诀为“左加右减，上加下减”．(2)对称变换①y＝f(－x)，y＝－f(x)，y＝________－f(－x)三个函数的图象与y＝f(x)的图象分别关于________、________、________对称；②若对定义域内的一切x均有f(m＋x)＝f(m－x)，则y＝f(x)的图象关于直线________对称．(3)伸缩变换①要得到y＝Af(x)(A>0)的图象，可将y＝f(x)的图象上每点的纵坐标伸(A>1时)或缩(A<1时)到原来的_____________；②要得到y＝f(ax)(a>0)的图象，可将y＝f(x)的图象上每点的横坐标伸(a<1时)或缩(a>1时)到原来的_____________．(4)翻折变换①y＝|f(x)|的图象作法：作出y＝f(x)的图象，将图象位于x轴下方的部分以x轴为对称轴翻折到x轴上方，上方的部分不变；②y ＝f (|x |)的图象作法：作出y ＝f (x )在y 轴右边的图象，以y 轴为对称轴将其翻折到左边得y ＝f (|x |)在y 轴左边的图象，右边的部分不变． 自查自纠：2．(1)①y ＝f (x ＋a ) 右 ②y ＝f (x )＋b 下 (2)①y 轴 x 轴 原点 ②x ＝m (3)①A 倍 ②1a 倍二、应用题型题组一：1．已知函数|)|(x f y -=的图像如左图所示，则函数)(x f y =的图像不可能．．．是（ ）(1)(2)(3)(4)A.（1）B.（2）C.（3）D.（4） 2 ）A. B. C. D.3．函数y =xa x |x|(0<a <1)的图象的大致形状是（ ）A. B. C. D.4．曲线的部分图像是（ ）21||y x =+5．函数)(x f y=的图象如图所示，则函数)(log21x f y =的图象大致是（ ）6．如果我们定义一种运算： 已知函数，那么函数y=的大致图象是（）课堂检测： 1.函数的图像大致是（ ）2．函数1()1f x x=+的图象是（ ）3．函数的图象大致为（）A ．B ．C ．D ．g g h h ⎧⊗=⎨⎩(),(),g h g h ≥<()21x f x =⊗(1)f x -()21,01,03x x x f x x ⎧-+<⎪=⎨⎛⎫≥⎪ ⎪⎝⎭⎩题组二： 1．函数()21x fx e -=（e 是自然对数的底数）的部分图象大致是（ ）2．函数xx x y sin cos +=的图象大致为（）12）课堂检测： 3．函数的图象大致是（ ）4．函数()1cos f x x x x ⎛⎫=-⎪⎝⎭（x ππ-≤≤且0x ≠）的图象可能（ ） xln5．函数()2sin 1xf x x =+的图象大致为（ ）6．函数221ln )(x x x f -=的图象大致是（ ）7．函数()ln f x x x =的大致图像为（ ）8．函数2()(2)x f x x x e =-的图像大致是（ ）题组三：1．函数y kx b =+与函数kby x=在同一坐标系中的大致图象正确的是（）2．已知0,0a b >>，且1ab =则函数()x f x a =与函数()log b g x x =-的图像可能是（）3．已知0a >，1a ≠，函数log ay x =，x y a =，y x a =+在同一坐标系中的图象可能是（ ）4 ）5．在同一个坐标系中画出函数x a y =，ax y sin =的部分图像，其中0>a 且1≠a ，则下列所给图像可能正确的是（ ）课堂检测：1． 在同一坐标系中画出函数a x y a yx +==,的图象, 可能正确的是（ ）2．若函数()log ()a f x x b =+（其中,a b 为常数）的图象如右图所示，则函数()x g x a b =+ 的大致图象是3．已知函数))(()(b x a x x f --=（其中b a >）的图象如图所示，则函数b a x g x +=)(的图象是图中的（ ）A B C D题组四：1．“龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点.用S 1、S 2分别表示乌龟和兔子所行的路程，t 为时间，则与故事情节相吻合是（ ）2．如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x 轴的直线)0(:a t t x l ≤≤=经过原点O 向右平行移动,l 在移动过程中扫过平面图形的面积为y （图中阴影部分）,若函数)(t f y =的大致图像如右图,那么平面图形的形状不可能是y=f (x )3．如图，点在边长为的正方形ABCD 的边界上运动，设是CD 边的中点，当点P 沿着M C B A ,,,匀速率运动时，点P 经过的路程x 为自变量，三角形APM 的面积为y ，则函数()y f x 图像的形状大致是（ ）.4．如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上，过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设BP x =，MN y =，函数()y f x =的图象大致是( )课堂检测：1．某工厂从2000年开始，近八年以来生产某种产品的情况是：前四年年产量的增长速度越来越慢，后四年年产量的增长速度保持不变，则该厂八年来这种产品的年产量y 可用图像表示的是（ ）.2．如图：ABC ∆为等腰直角三角形，90ABC ∠=︒.直线l 与AB 相交.且l AB ⊥，直线l 截这个三角形所得的位于直线右方的图形面积为y .点A 到直线l 的距离为x .则()y f x =的图像大致为（ ）P 1M MA BD C P3．如图所示，设点A是单位圆上的一定点，动点P从点A出发在圆上按逆时针方向旋转一周，点P所旋转过的弧AP的长为l，原点O到弦AP的长为d，则函数d＝f（l）的图像大致是( )三、课外作业：1．下列函数图象中不正确的是（）2．已知函数()ln xf x e=，则函数()1y f x=+的大致图象为（）34．下列图象中，可能是函数图象的是（ ）5．函数的图象大致是（ ）6．定义运算“*”为：,0,2,0a b ab a a b a +<⎧⎪*=⎨⎪⎩≥.若函数()(1)f x x x =+*，则该函数的图象大致是（ ）．7．函数2y ax bx 与log bay x = (0,||||)ab a b ≠≠在同一直角坐标系中的图象可能是（ ）8．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后为了赶时间加快速度行驶．与以上事件吻合得最好的图象是（ ）x xx xe e y e e---=+22x y x =-A ．B ．C ．D ．9．如图，一高为H 且装满水的鱼缸，其底部装有一排水小孔，当小孔打开时，水从孔中匀速流出，水流完所用时间为.T 若鱼缸水深为h 时，水流出所用时间为t ，则函数()h f t =的图象大致是( )A ．B ．C ．D ．解析二、应用题型题组一：1．已知函数|)|(x f y -=的图像如左图所示，则函数)(x f y =的图像不可能．．．是（ ）(1)(2)(3)(4)A.（1）B.（2）C.（3）D.（4） 【答案】C【解析】由题意得当x ＜0时，|)|(x f y -=与函数f （x ）的图像一致，故选C 。

初中数学比赛专题选讲（初三.17）函数的图象一、内容概要1.函数的图象定义：在直角坐标系中，以自变量 x 为横坐标和以它的函数坐标的点的会合，叫做函数y=f(x) 的图象 .比如一次函数 y=kx+b (k,b 是常数， k ≠0)的图象是一条直线 l.① l 上的任一点 p0(x0,y0) 的坐标，合适等式y=kx+b, 即 y0=kx 0+b ；②若 y1=kx 1+b，则点 p1(x 1,y1)在直线l上.2. 方程的图象：我们把y=kx+b 看作是对于 x, y 的二元一次方程 kx － y+b=0, 那么直线 l 就是以这个方程的解为坐标的点的会合，我们把这条直线叫做二元一次方程的图象.二元一次方程 ax+by+c=0 (a,b,c 是常数， a≠ 0,b≠ 0) 叫做直线方程一般地，在直角坐标系中，假如某曲线是以某二元方程的解为坐标的点的会合，那么这曲线就叫做这个方程的图象. 比如：y的对应值为纵ylP(x,y)o x .二元二次方程y=ax 2+bx+c(a ≠ 0) (即二次函数 )的图象是抛物线；二元分式方程y= (k ≠ 0) (即反比率函数 )的图象是双曲线 .3. 函数的图象能直观地反应自变量x 与函数 y 的对应规律 . 比如：①由图象的最高，最低点可看函数的最大，最小值；②由图象的上涨，降落反应函数y 是随 x 的增大而增大 (或减小 )；③函数 y=f(x) 的图象在横轴的上方，下方或轴上，分别表示y>0,y<0,y=0. 图象所对应的横坐标就是不等式 f(x)>0,f(x)<0 的解集和方程 f(x)=0 的解 .④两个函数图象的交点坐标，就是这两个图象所表示的两个方程(即函数分析式 )的公共解 .等等4.画函数图象一般是：①应先确立自变量的取值范围.要使代数式存心义，并使代数式所表示的实质问题有意义，还要注意能否连续，能否有界.②一般用描点法，但对一次函数 (二元一次方程 )的图象，因它是直线 (包含射线、线段 )，因此可采纳两点法 .线段必定要画出端点 (包含临界点 ).③对含有绝对值符号 (或其余特别符号 )的分析式，应按定义对自变量分区议论，写成几个分析式 .二、例题例 1. 右图是二次函数 y=ax2 +bx+c (a≠ 0)，试决定 a, b, c 及 b2－ 4ac 的符号 .解：∵抛物线张口向下，∴ a<0.∵对称轴在原点右侧，∴x=－ >0 且 a<0,∴b>0.∵抛物线与纵轴的交点在正半轴上，∴截距 c>0.∵抛物线与横轴有两个交点，∴ b2－ 4ac>0.例 2. 已知：抛物线 f ： y= － (x－ 2)2+5.试写出把 f 向左平行挪动 2 个单位后，所得的曲线 f 1的方程；以及 f 对于 x 轴对称的曲线 f 2 的方程 . 画出 f 1和 f2的略图，并求：（ 1）x 的值什么范围，曲线 f 1和 f2都是降落的；（ 2）x 的值在什么范围，曲线 f 1和 f2围成一个关闭图形；（ 3）求在 f 1和 f2围成关闭图形上，平行于y 轴的线段的长度的最大值 .（ 1980 年福建省中招试题）解： f1 ： y=－ x2+5 (由极点横坐标变化确立的)，f2： y=(x － 2)2－5 (由张口方向相反确立的).（1）当 x≥ 0 时， f1降落，当x≤2 时， f2降落，∴当 0≤x≤ 2 时，曲线f1和 f 2都是降落的 .（ 2）求两曲线的交点横坐标，y x25，即解方程组y (x 2)2 5.x2－ 2x－3=0 .∴x= － 1；或 x=3.∴当－ 1≤ x ≤3 时，曲线 f 1和 f2围成一个关闭图形.(3)关闭图形上，平行于y 轴的线段的长度，就是对应于同一个横坐标，两曲线上的点的纵坐标的差.在区间–1≤ x ≤ 3 内，设 f 1上的点 P1(x,y 1 ), f2 上的点 P2(x,y 2) ，求 y1－ y2 的最大值，可用配方法：y1－ y2 ＝ ( －x2+5) － [ (x －2) 2－ 5]＝－ 2x2+4x+6＝－ 2(x－ 1)2+8.∵－ 2<0，∴ y － y 有最大值 .1 2当 x=1 时， y1－ y2的值最大是 8.即线段长度的最大值是8.例 3. 画函数 y= x 1 x 2的图象.解：自变量 x 的取值范围是全体实数，下面分区议论：当 x< － 1 时，y=－ (x+1) － (x－ 2)= － 2x+1；当－ 1 ≤ x<2 时，y=x+1 － (x－ 2)=3 ；当 x ≥ 2 时，y=x+1+x －2=2x － 1.2x 1( x 1)；即 y= x 1 x 2 =3( 1 x 2)；2x 1( x 2).x － 2 － 1 2 3y=－ 2x+1 (x< － 1) 5 3y=3( －1≤ x<2) 3 3y=2x － 1(x≥ 2) 3 5∴画函数 y= x 1 x 2 的图象以以下图：例 4. 画方程 [x] 2 +[y] 2=1 的图象，[m]表示不超出m 的最大整数 .(1985 年徐州市初中数学比赛题解：∵ [x] 2≥ 0， 且[y] 2 =1－[x] 2≥ 0，∴ [x] 2≤ 1 .∴ 0≤ [x] 2≤ 1.∵ [m] 表示不超出 m 的最大整数， ∴当 [x] 2 =0[x]=00≤ x ≤ 1 .当 [x] 2=1[x]=1( 1 x 0)，1(1 x 2).自变量 x 的取值范围是：－ 1≤ x<2.部分的x－1≤ x<0 0 ≤ x<11≤ x<2 四个正方形， [x]－ 11方程的[x]211 图象 .[y] 2=1 －[x] 21正方形[y]0 － 1 1 0 左、下界限，y0≤ y<1－ 1≤ y<0 1≤ y<2 0≤ y<1正方形右、上界限 . 例 5.直线 y=x+m 与双曲线 y= m在第一象限订交点A ， S Rt △ AOB =3.x① 求 m 的值 ；②设直线与 x 轴交于点 C ，求点 C 的坐标； ③求 S △ABC .解： ①设 A 坐标为(x, x+m).∵ S △ AOB = 1OB × BA.231x( x m) ∴2mx mx整理得x 2 mx 6 0 x 2 mx m).如图暗影就是所求只包含各不包含各∴ m=6② ∵直线与 x 轴交于点 C. 把 y=0 代入 y=x+6 得 x= － 6,∴点 C 的坐标是 (－ 6，0) ③∵直线 y=x+m 与双曲线 y=m在第一象限订交点A ，xy x 63 156x解方程组得315yx y即点 A 的坐标是(－3+ 15 ，3+ 15 ).∴ BC= 63 15 =3+ 15∴ S △ABC =1(3+15 )(3+ 15 )=12+3 15 .2例 6.选择题 (只有一个正大确的答案 ).①函数 y=kx+k 与 y=k在同一坐标系中的图象的大概地点是()x② 函数 y=1－ x x 2的图象是 ()解：①常数k 是同一个值，.双曲线y=k在一、三象限，k>0,那么y=kx+k中，x当k>0时，直线上涨且在y 轴上的截距为正.因此应选(D) ；②注意到y=1 －xx 2中， 当x=0和x=1时y 有最大值1，应选(A).三、练习1. 填空：① 横坐标为－ 2 的点的会合，记作直线＿＿＿＿＿，纵轴记作直线＿＿＿＿＿＿，横轴记作直线＿＿＿＿＿，横坐标与纵坐标互为相反数的点的会合是直线＿＿＿＿＿＿，经过一、三象限，均分两坐标轴夹角的直线记作方程＿＿＿＿＿＿＿.② 点 P （ x, y ）对于横轴的对称点 P 1 的坐标是（ ），点 P 对于原点的对称点 P 2 的坐标是（ ） .③ f ： y=3(x － 2)2+5,对于横轴对称的抛物线f 1 记作＿＿＿＿＿＿＿f 对于原点对称的抛物线f 2 记作＿＿＿＿＿＿＿ .，） .④ A （ 1， 3）对于直线 y=x 的对称点 A 的坐标是（点 B （－ 2， 3）对于直线 y= － x 的对称点 B ，的坐标是（ ） .2. 依据图象地点判断指定的常数的符号① 直线 y=kx+b 经过二、一、四象限，则k,b 的符号是＿＿＿＿＿＿② 抛物线 y=ax 2+bx+c 的地点，以下图，试确立以下代数式的符号b______,b______,c_______,a__, －2ab 2－ 4ac______,4ac b 24a ______bb 2 4ac2a _____3. 选择题（只有一个正确的答案）（ 1）以下图（ 1）是一次函数 p x+qy+r=0（ A ） p=q, r=0 . (B) p= － q,的图象，以下条件正确的选项是（r=0. (C)p=q, r=1.） .(D) p= － q, r=1.（ 2）以下图（ 2）是二次函数y=ax 2+bx+c 的图象，以下答案哪个正确？（）（A ） a+b+c=0.（B）a+b+c<0.（C）a+b+c>0.（D）a+b+c值不定.(1)（ 3）二次函数y=a(x+m) 2+n 中， a>0 , m>0, n>0它的图象（）(4)两个一次函数 y=mx+n y=nx+m 且 mn<0, 那么它们在同一坐标系内的图象大概为（）（ D）（ 5）在同一坐标系内，y=ax+b 与 y=ax2+b 的图象大概地点是（）(6) 已知函数 y+ax+b 和 y=ax2 +bx+c 那么它们的图象是（）（ 1983 年福建省初中数学比赛题）4.画以下函数的图象① y= x2；②y=x2；③ y=(x )2；④y=－x . x5.有 m 部相同的机器，同时开始工作，需要任务，求所需的时间 y(小时 )与机器台数时函数的图象 .m 小时达成某项任务 .设由 x 部机器达成某一 x(x 为小于 m 的整数 )的函数关系，并画出当 m=56. 画以下方程、函数的图象. ①x y 2 ；②y=x2－2|x|－3.7. 这是一张追及图看图回答：①谁追及谁？②谁早出发，早几小时？③甲、乙在这段行程速度各多少？④追的人从出发到追上，用了几小时？走多少行程？S公里⑤分别列出甲、乙两人的行程y 甲， y 乙和时间 x 的函数关系的分析式 .8. 如图，抛物线 1 2 和抛物线 2 2 的地点以下图 .L ： y=ax +2bx+c L ： y=(a+1)x +2(b+2)x+c+3① .判断哪条抛物线经过A、 B、 C 三点，说明原因；② .求出点 B 和点 C 的横坐标；2 255b, c 的值 .③ .若 AB ＝BC ， OC＝ OD，求 a,20 x 2 x 9 9. 坐标平面上，纵坐标与横坐标都是整数的格点(整点 )，试在二次函数y=1510 10 5的图象上找出10知足甲x 的全部整点(x,y), 并说明原因 . y5 乙(1995 年全国初中数学联赛题 )（ 8）-5 0 1 2 3 45t小时10C D练习题参照答案1. ① x= － 2, x=0,y=0, y= － x,y=x ；② (x,y),( － x, － y) ；③ y=－ 3(x － 2)2－ 5, y= － 3(x+2) 2－ 5 ④ (3，1)， (－3， 2)2. ① k<0, b>0. ②正，负，正，负，负，正，负.3. ①(A)，② (B)，③(B) ，④ (C)，⑤ (D) ，⑥ (C)4. ①∵ x≠ 0，∴图象不以过原点；②y≥0；③ x≥ 0；④y≤ 0.m 25. y=(x 是正整数x≤ m=5).x6.（如图）7. ①乙追及甲；②甲先1小时；③时速甲4、乙5千米；④乙用 4 小时追上甲先走的 4 千米⑤ y 甲 =4x, y 乙 =5x8. ①∵由图象 a,a+1 异号，∴ L 2过 A ， B， C 三点 . ②－ 3，－ 1. ③－1，0，1.3 39.(2， 2)， (4， 3)， (7，6)， (9， 9)， (－ 3， 3)， (－ 6，6). 由 x2－ x+18≤ 10 x .当 x≥0 时， x2－x+18 ≤ 10x, x2－ 11x+18≤0,(x－ 2)(x－ 9)≤ 0，2≤ x≤ 9, 这时，有 4 个整数点： (2， 2) ，(4， 3)， (7， 6)， (9， 9)；当x<0 时， x2－ x+18≤－ 10x, x2＋ 9x+18 ≤ 0，（ x+6 ）(x+3) ≤ 0，－ 6≤ x≤－ 3,这时有两个整数点：(－ 3， 3)， (－ 6， 6).。

2024年初中数学函数与图像题型解析在初中数学的学习中，函数与图像是一个非常重要的知识点，也是中考的重点和难点之一。

对于很多同学来说，函数与图像的题型可能会让人感到困惑和头疼，但只要我们掌握了正确的方法和技巧，就能够轻松应对。

首先，我们来了解一下什么是函数。

简单来说，函数就是一种特殊的关系，在这种关系中，对于一个自变量的每一个取值，都有唯一的因变量的值与之对应。

比如，y ＝ 2x 就是一个函数，当 x 取 1 时，y就等于 2；当 x 取 2 时，y 就等于 4。

而函数图像则是将函数关系用图形的形式表示出来。

通过观察函数图像，我们可以更直观地了解函数的性质和特点。

常见的函数类型有一次函数、二次函数和反比例函数。

一次函数的表达式为 y ＝ kx ＋ b（k、b 为常数，k ≠ 0）。

它的图像是一条直线。

当 k ＞ 0 时，函数图像从左到右上升，y 随 x 的增大而增大；当 k ＜ 0 时，函数图像从左到右下降，y 随 x 的增大而减小。

比如，给出一次函数 y ＝ 3x 1。

我们可以先确定其斜率 k ＝ 3 ＞ 0，所以函数图像是上升的。

然后，当 x ＝ 0 时，y ＝－1，这就是函数图像与 y 轴的交点（0，－1）。

再令 y ＝ 0，解得 x ＝ 1/3，这就是函数图像与 x 轴的交点（1/3，0）。

有了这两个点，我们就可以画出函数的图像。

二次函数的一般式为 y ＝ ax²＋ bx ＋ c（a、b、c 为常数，a ≠ 0）。

它的图像是一条抛物线。

当 a ＞ 0 时，抛物线开口向上；当 a ＜ 0 时，抛物线开口向下。

以二次函数 y ＝ x² 2x 3 为例。

我们可以通过配方法将其化为顶点式：y ＝（x 1)² 4，从而得到顶点坐标为（1，－4）。

然后求出与 x轴的交点，令 y ＝ 0，即 x² 2x 3 ＝ 0，解得 x ＝－1 或 x ＝ 3。

这样就能画出大致的图像。

初中数学之函数图像题必考5种类型（含答案）类型一根据函数性质判断函数图象1.若关于X的一元二茹:方程^ + 1=0自两亍不栩籌的真劉根,则一衣画畑=尿十勺的大致图象可能是］＞A B C Ds二衣函数十紙十「的屈象在平面直角塑标系中的楼畫如图所示，则一孜国劉+ b与反比例函数冋一年頂自角半标系中的图象可能昴类型二分析实际问题判断函数图象试&农练1•如囲把一个小球垂直向丄葩岀，则下列描述该小球的运动速皮°（单位：H1S）与运动时问K单位，＜）关系的因数團象中，正确的是A B C D2・"黄金1诗”玉深种子的价格为5元汁克，如果一次购买2干克以上的种子, 韶过2千克部分的种子价格打0折，设购买种子数量为"千兗，的隸金额対）•元，別，与二的函數天系的磁大致罡（）A B C D70 58 2 M乳如^辺、眈辞＜3 0的两条与梱乖有訓育龟点P 从点0暗屈—0 的踣些匀遵巨动，谡乂*片」询补 團，那么:与P 运动的何同匚望位：期的关 轟酹： （）3，结合几何图形中的动点问题判断函数的图像1.如创所示，布平砒胡小中.帝育干对命塔的肯埔4从点J5幵姑;fl 看昨 遵啟）匀速平彩到点巧嘏直站『被』酬BHfi 址段£f 的畑为m 运血寸何为心刚 」咲于『的因戟的大致蘇罡t 01 iDBC-4,旦P 長M AE 1■一动点.2/面帜舟二剣T 列囲象中A B C D工如囲'已知八4%为等边三角形，4B=19 6 D 为边“上一点“过点。

作DEIIAC,艾BC 干E 点，过E 点作护丄交肿的延长线于F ©、•设・3二心△2)打的面积为厂则能大致反映J 与w 的因数关系的圉象是()5•如用.iF 方彫.“CQ 的询长为3 cm,动点尸从万点出发以3 cm/5的建启沿看 边BC-CD-DA 运动，到达*点停止运动；另一动点0同时从B 点出发，以女皿 的速度沿看边血冋4点运劝，到达-4点停止运功一设P 点运加何为R), /XBPQ 的面积为Xcn?),別y 关于"的的数囹衆杲沪4廿牯第4题囹D类型四分析雷数图象判断结论正误试題茨等1.删川=如叭朴的團毅加團所示'则下列说法酣鑽的恵）A.曲曲数團象的交点」坐肚禹亡.」）基”当X>1时,C.当x=l时，BC=3执当上逐笳増大附，n雷看丄啲旳:而賭大，F倔若左的增丈而孫小:.如囲①》E^&.iBCD边a上一点，点戶从点/帖折线恥―册-叱运动刘鱼广时停止「直Q从克E沿就?运adJ^Jfi广时停止，它ri抵功的遵度半睫若P、©同时JT始运孤识正动时间为斶,ABPQ的面帜为ygj已知占啲函数关系圃按如图②.则下列箔论溶误的是（）生.<£-« f IM B SinZjWTg 扌, 7匸当°<虑1呎」=?1D、当t=12s时，APEA是等腰三角形第2题圉拓展类型分析函数国角判新几何国形试题演纺1.匀速地向个容器內注水，最后把容器注满，在注水过程中,水面高度h随时间『的变化如图所亦（團中O4B「为一折钱），这个容器的形状是卜图中哪f （）a e ©A B C D2.点/从点0出发，披逆时针方向沼團K为Z的囹形运动周，0、P两点问的跑宴y与点P走过的賂程=・的曲数关彳如图"那么点P折走的图形是（）【答案】类型一根据函数性质判断函数图像试越液塔1.B【解析】丁"一2\+■肋4匸0有两个不相等的真数根，A4-伽-l=-dWM), 7、0异号冃均不为0,弁析各诜顷可知：A.由图象知，*>0, D>0,故北选J页错気 B.由豳知，A>0,b<0,故此迭项正确,C.由同象知，k<0, X),故此选项错误§D宙豳知,g b=O,故此选项错误_2.C【解析】丁幻“，.•.反比例国執L冊布在第二、四象眼，又VA2X) H国数J=^v-1经过(0, -1), /.直线尸址一1经过第一、三、囚象眼，故选C.3 .C【齋析】观祭一次餉的图象知其幵L1I可下，最X"拜冃剤种右侧，所以-缶0,故於0,与J轴的交点礼轴正半轴，故。