第52讲 空间距离及其计算、折叠问题
- 格式:ppt
- 大小:3.30 MB
- 文档页数:66

空间折叠空间折叠是一种因为强大的引力使空间发生扭曲的现象。
这种现象是真实存在的,因而在理论上只要能达到一定的引力就能使空间发生弯曲,就好比要从一张平整的纸一端到另一端除了走两点间的直线外,还可以直接把纸叠起来,让两点靠近。
因此人们普遍认为黑洞能够穿越遥远的空间,因为黑洞具有无法比拟的巨大引力,连光都不可避免的被它巨大的引力吸引,那么在这样的引力下空间也有极大的可能被折叠,这也就使得以不超越光速却能在短时间内进行宇宙旅行成为了可能。
中文名空间折叠原因强大的引力结果空间发生扭曲特点真实存在的结果短时间内进行宇宙旅行目录1. 1 空间折叠简介2. 2 新闻资讯3. 3 举例1. 4 详细了解2.▪发现3.▪基础浅析4.▪瞬间移动1.▪艺术2. 5 时空旅行3. 6 出现过的作品空间折叠简介空间折叠在《哆啦A梦·大雄的宇宙开拓史》中有相关说明,《哆啦A梦》中称为“翘曲空间”。
(做时空转换时所经历的空间。
一张纸上的两个点,之间的距离记作a。
如果你把纸弯曲,使这两个点重合,那么这两个点的距离就是0,而不是刚开始的纸面上的距离a。
这就是空间翘曲。
可以进行瞬间移动。
科技水平无法实现。
这样使扭曲的空间就是翘曲空间)“……星球与星球之间,都相隔几光年至几十万光年。
因此,宇宙飞船即使是以光速飞行,也要用几年至几十万年。
如果只靠重力控制飞行,当然太慢了……但是,如果反复翘曲空间就可以更快地到达目的地。
”新闻资讯人们的宇宙空间是一个以真空基态为界。
若飞行器可以进入异矢量方向上的世界,则从人们的世界中消失。
之后的飞行器的速度相对我们而言是超极限大的。
当一定时间之后,飞行器重新回到我们的世界。
而这个过程,我们产生折叠飞行的错觉。
实际上飞行器飞过的路程尺度没有改变,只是在同样路程的花用时间上少了。
而当飞行器在负能量的世界时,飞行器的类性也成负能量体。
在宇宙大爆炸的前后一段时间里,光子的速度更加快。
其中主要原因是背景空间的能场(也可能是U惯性系能场)比背景空间的能场高。

空间几何中的距离公式在空间几何中,距离公式是计算两点之间距离的重要工具。
距离公式不仅广泛应用于数学领域,还在物理学、工程学等各个领域发挥重要作用。
本文将详细介绍空间几何中的距离公式,包括二维空间和三维空间中的情况。
一、二维空间中的距离公式在二维空间中,我们可以使用欧几里得距离公式来计算两点之间的距离。
假设有两点A(x1, y1)和B(x2, y2),它们之间的距离可以通过以下公式来计算:d = √((x2 - x1)² + (y2 - y1)²)其中,d表示两点之间的距离。
以一个例子来说明。
假设有两个点A(2, 3)和B(5, 7),我们可以使用距离公式计算它们之间的距离。
根据公式,我们有:d = √((5 - 2)² + (7 - 3)²)= √(3² + 4²)= √(9 + 16)= √25= 5因此,点A和点B之间的距离为5个单位长度。
二、三维空间中的距离公式在三维空间中,我们可以使用三维欧几里得距离公式来计算两点之间的距离。
假设有两点A(x1, y1, z1)和B(x2, y2, z2),它们之间的距离可以通过以下公式来计算:d = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)以一个例子来说明。
假设有两个点A(1, 2, 3)和B(4, 5, 6),我们可以使用距离公式计算它们之间的距离。
根据公式,我们有:d = √((4 - 1)² + (5 - 2)² + (6 - 3)²)= √(3² + 3² + 3²)= √(9 + 9 + 9)= √27= 3√3因此,点A和点B之间的距离为3√3个单位长度。
距离公式在空间几何中有着广泛的应用。
在实际问题中,我们经常需要计算两点之间的距离,比如在导航系统中计算两地之间的距离,或者在建筑工程中计算两个点之间的距离等。
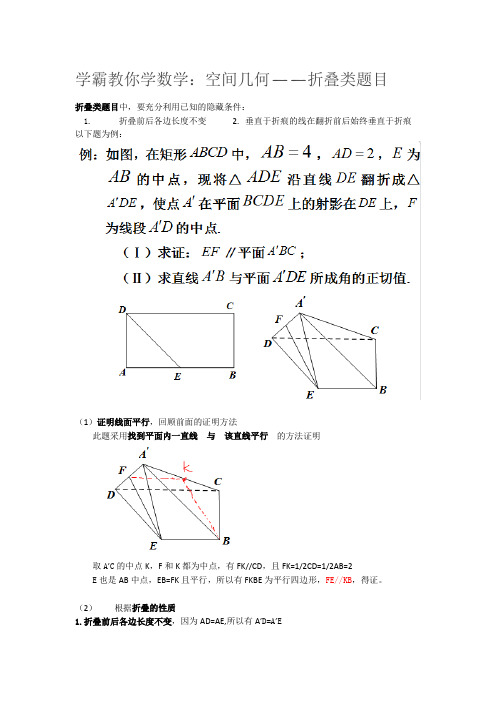
学霸教你学数学:空间几何——折叠类题目折叠类题目中,要充分利用已知的隐藏条件:1. 折叠前后各边长度不变2. 垂直于折痕的线在翻折前后始终垂直于折痕以下题为例:(1)证明线面平行,回顾前面的证明方法此题采用找到平面内一直线与该直线平行的方法证明取A’C的中点K,F和K都为中点,有FK//CD,且FK=1/2CD=1/2AB=2E也是AB中点,EB=FK且平行,所以有FKBE为平行四边形,FE//KB,得证。
(2)根据折叠的性质1.折叠前后各边长度不变,因为AD=AE,所以有A’D=A’E2.垂直于折痕的线在翻折前后始终垂直于折痕:这题的折痕是DE,过A作AH垂直于DE,在等腰直角三角形AED中,就有H是DE的中点。
过A’作A’G垂直于DE,根据这个性质,G 和H就是同一点,也就是DE的中点根据题目所说,A’的投影在DE上,就可以确定A’H垂直于底面DEBC再通过建系解出此题。
建系的坐标系选取方法有很多,尽量选择可以方便写出面的法向量或者各个点的坐标的X、Y、Z轴。
如图建系,就可以直接得出面A’DE的法向量为n=(0,1,0)。
此题的答案是:正切值( θ=)为,做对了吗?(如果是用上面的建系方法,可以核对下面的坐标是不是写对了:A’(0,0,),B(2,,0) , | sin|=, cosθ=,tanθ=)另外,也可以尝试不用建系法求解。
建系法的常用公式:1、求线段的长度:|AB|= =2、求P点到平面α的距离:|PN|=(N为P到平面的垂足,M 为平面上任意一点,n为平面α的法向量)3、求直线l 与平面α 所成的角θ:| sinθ|=( n为α的法向量)4、求两异面直线AB 与CD的夹角θ:cosθ=5、求两个平面的二面角θ(方法一)| cosθ |=(n1,n2为两个面的法向量)补充:求两个平面的二面角θ还有一种方法:射影面积法cosθ =实例:求面A’BC和面α的二面角θ:cosθ = = (其中A 是A’在面α上的投影)。

空间折叠题公考技巧
随着科技的不断进步,空间折叠这项技术也逐渐走入人们的生活。
空间折叠是将物体从一个空间传送到另一个空间的技术,它可以将两
个地点之间的距离缩短至极限,让人们在短时间内到达遥远的地方。
目前,这项技术已经在科幻小说和电影中被广泛运用,但它的应用领
域正在不断扩展。
空间折叠的实现需要强大的能量与复杂的技术,它的实现有着许
多限制,其中最主要的一项是空间折叠只能在特定条件下进行。
因此,空间折叠技术主要用于军事、航天和科研领域。
在军事上,空间折叠
技术可以快速、安全地将装备和士兵传送到远程位置,实现快速投送。
同时,空间折叠还可以使军事通讯更加安全,防止敌人截获信息。
在
航天领域,空间折叠技术可以将宇航员传送到深空探测器中,帮助人
类更深入地探索太空。
而在科研领域,空间折叠技术可以协助科学家
进行超长距离的实验和观测,解开更多的科学之谜。
随着技术的不断发展,空间折叠技术的应用领域也不断扩展,有
望在未来进一步推动人类社会的发展。
然而,空间折叠也产生了一些
问题和风险。
例如,可能会出现空间折叠传送出错或引发空间漩涡等
问题,这些都需要技术上的完善和严密的管理。
此外,空间折叠技术
的广泛应用还需要考虑道德和伦理问题,例如如何保障人类自身的安
全和尊严等。
最后,我们可以看到,空间折叠技术虽然在现实生活中还有一些
限制和风险,但它作为一项高新技术,在未来有望为人类创造更多的
机遇和发展空间。
我们需要保持谨慎和审慎的态度,把技术应用于各
个领域,为推动人类社会的发展做出更多的贡献。

错误!A1B1C1D1中,若AB=BC=a,AA1=2a,则点A到直线A1C的距离为 Ca aa a解析:如图,点A到直线A1C的距离,即为Rt△A1AC斜边上的高AE由AB=BC=a,得AC=错误!a又AA1=2a,所以A1C=错误!a,所以AE=错误!=错误!aA1B1C1D1的底面边长为1,AB1与底面ABCD成60°角,则直线A1C1到底面ABCD的距离为 DB.1解析:直线A1C1∥平面ABCD,A1C1到底面ABCD的距离即为正棱柱的高h,tan 60°=错误!,所以h=错误!,故选D3改编已知1、2是两条异面直线,α、β、γ是三个互相平行的平面,1、2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,则DE= C解析:由面面平行的性质定理可得错误!=错误!,所以错误!=错误!,即错误!=错误!,所以DE=,故选C中,平面OAB的一个法向量n=2,-2,1,已知,N分别为AB,AC上的点,满足AM =AN=2,沿MN将△AMN折起,使得平面AMN与平面MNCB所成的二面角为60°,则A点到平面MNCB的距离为错误!解析:在△ABC中,过A点作AF⊥BC交BC于F点,交MN于E点,由题意知折叠后∠AEF即为平面AMN与平面MNCB所成的二面角的平面角,故∠AEF=60°,过A点作AH⊥EF 于H点,则AH即为A点到平面MNCB的距离,因为AE=错误!,所以AH=AE·in 60°=错误!72022·安徽怀宁检测在空间直角坐标系中,定义:平面α的一般方程为A+B+C+D=0A,B,C,D∈R,且A,B,C不同时为零,点分别为三条棱的中点,A、B是顶点,求点M到截面ABCD的距离.解析:设点M到截面ABCD的距离为h连接AC、AM,作CF⊥AB,垂足为F,连接CMV CABM=错误!S△ABM·CM=错误!×错误!×1=错误!又V MABC=错误!·错误!·AB·CF·h=错误!×错误!×错误!×错误!×h=错误!,故由V CABM=V MABC,得错误!=错误!,所以h=错误!92022·广东省珠海市上期期末矩形ABCD中,2AB=AD,E是AD的中点,沿BE将△ABE折起到△A′BE的位置,使A′C=A′D,F、G分别是BE、CD的中点.1求证:A′F⊥CD;2设AB=2,求四棱锥A′BCDE的体积.解析:1证明:矩形ABCD中,因为F、G分别是BE、CD的中点,所以FG∥BC,所以FG⊥CD因为A′C=A′D,所以A′G⊥CD,又FG∩A′G=G,所以CD⊥平面A′GF,所以CD⊥A′F2因为AB=2,所以BC=4,ED=2,在等腰直角三角形△A′BE中,A′F=错误!且A′F⊥BE,因为CD⊥A′F且BE、CD不平行,所以A′F⊥平面BCDE所以几何体A′BCDE的体积V A′BCDE=错误!A′F·S四边形BCDE=错误!×错误!×错误!×2=2错误!。
一、空间中的折叠类问题1.如图,圆形纸片的圆心为O ,半径为5cm ,该纸片上的等边三角形ABC 的中心为O 。
D,E,F 为圆O 上的点,△DBC,△ECA,△F AB 分别是以BC,CA,AB 为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB 为折痕折起△DBC,△ECA,△F AB ,使得D,E,F 重合,得到三棱锥,当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为。
2.已知一个三棱锥的六条棱的长分别为1,1,1,1,√2,a,且长为a 的棱与长为√2的棱所在直线的异面直线,则三棱锥的体积的最大值为()。
A.√212 B.√312 C.√26 D.√363.如图,一张A 4纸的长,宽分别为2√2a,2a,A,B,C,D 分别是其四条边的中点,现将其沿图中虚线折起,使得P 1,P 2,P 3,P 4四点重合为一点P .从而得到一个多面体,关于该多面体的下列命题,正确的是。
(写出所有正确命题的序号)①该多面体是三棱锥;②平面BAD ⊥平面BCD ;③平面BAC ⊥平面ACD ;④该多面体外接球的表面积为5πa 24.如图,在正方形ABCD 中,AC 为对角线,E,F 分别是BC,CD 的中点,G 是EF 的中点现在沿AE,AF 及EF 把这个正方形折成一个空间图形,使B,C,D 三点重合,重合后的点记为H ,下列说法错误的是。
(将符合题意的序号写在横线上)①AG ⊥△EF H 所在平面;②AH ⊥△EF H 所在平面;③HF ⊥△AEF 所在平面;④HG ⊥△AEF 所在平面。
5.如图,矩形ABCD 中,AB =2AD =4,E 为边AB 的中点,将△ADE 沿直线DE 翻转成△A 1DE ,构成四棱锥A 1−BCDE ,若M 为线段A 1C 的中点,在翻转的过程中有如下4个命题:①MB//平面A 1DE ;②存在某个位置,使DE ⊥A 1C ;③存在某个位置,使A 1D ⊥CE ;④点A 1在半径为√2的圆周上运动,其中正确命题的个数是()。