材料力学(金忠谋)第六版答案解析第07章
- 格式:doc
- 大小:1.04 MB
- 文档页数:25

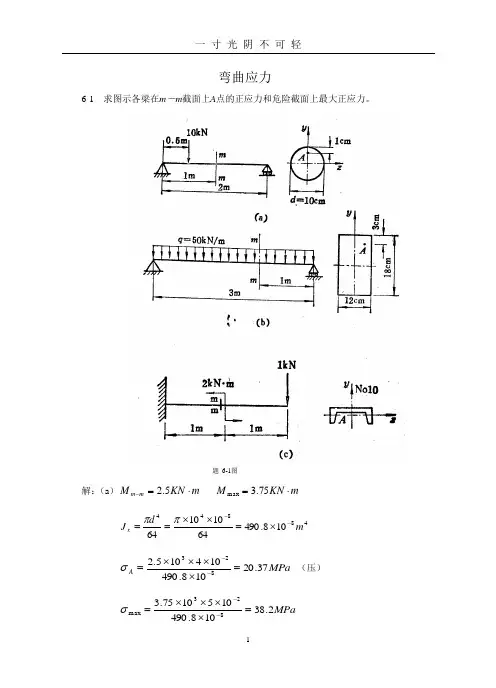
弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。

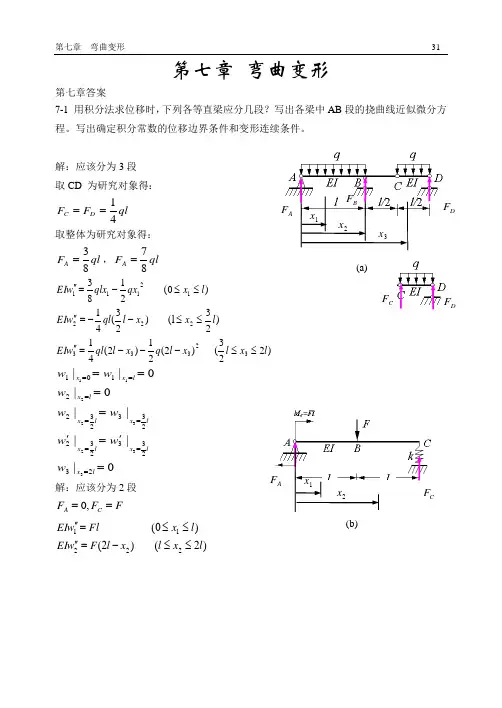
第七章 弯曲变形第七章答案7-1 用积分法求位移时,下列各等直梁应分几段?写出各梁中AB 段的挠曲线近似微分方程。
写出确定积分常数的位移边界条件和变形连续条件。
解:应该分为3段 取CD 为研究对象得:ql F F D C 41==取整体为研究对象得:ql F A 83=,ql F A 87= )223( )2(21)2(41)23(l )23(41)(0 21833233322212111l x l x l q x l ql w EI l x x l ql w EI l x qx qlx w EI ≤≤---=''≤≤--=''≤≤-=''0|||||0|0||23233232233232210133232211='='============l x lx lx lx lx l x l x x w w w w w w w w解:应该分为2段F F F C A ==,0)2( )2()(0 22211l x l x l F w EI l x Fl w EI ≤≤-=''≤≤=''1x x AF DF BF DF(b)AF 1xkFw w w w w w l x l x l x l x l x x -='='========22212101232321|||||0| 7.2 用积分法求图示梁跨度中点的挠度c w 和端截面转角A θ及B θ。
(EI ql w C 76854=,EI ql A 38473=θ,EI ql B 12833-=θ)解:ql F A 81=;ql F B 83=1113111211111 481 161)2(0 81D x C qlx EIw C qlx w EI l x qlx w EI ++=+='≤≤='' 2224232223222222222 )2(241 481 )2(61 161)2( )2(21 81D x C l x q qlx EIw C l x q qlx w EI l x l l x q qlx w EI ++--=+--='≤≤--='' 边界条件:0|011==x w ⇒ 01=D 0|22==l x w ⇒0 162414812244=++⋅-D l C ql ql 222132||l x l x w w ===⇒2211)2( )2(D l C D l C +=+ 222132||l x l x w w =='='⇒021==C C则:021==D D ,4213847ql C C -== 32111133113847 161)2(0 3847 481qlqlx w EI l x x ql qlx EIw -='≤≤-=3847)2(61 161)2( 3847)2(241 48133222222342322ql l x q qlx w EI l x l x ql l x q qlx EIw ---='≤≤---= AF BF1xEI ql w x A 3847|3011-='==θ EI ql w l x B 1283|322='==θ EIql l ql l ql EI w w C 3845)]2(3847 )2(481[13331-=-==7.3 用叠加法求下列各梁的指定位移。

材料力学(金忠谋)第六版答案- 附录2]附录I 截面图形的几何性质I-1求下列截面图形对 z 轴的静矩与形心的位—置。
(b )解:(a )S zbt(h 2)htt(b(h 2)号)y ct(b(h2) h)t(bb(h2)b h3D 2{2[(〒D 2 (7)](2邑 (3 (3D)2字金卫D 3/D 、2〃 192(7)S zyc ~AH D 3________ 192 D D 3D 2 2( ) — [( )2 4 4 2 40.1367D(c)+h+S z(b t) t2 htht[(b t) 2s z _ (b-t)t + h27 - 2(/? + /,-/)1-2试求(1)图示工字形截面对形心轴y及的惯性矩厶与厶。
(2)图示卩字形截面对形心轴的惯矩与厶。
_hh3 (h-t)(h-2t)3胡3_(—2川一12 一\22tb3 (h - 2t)(t)y t(2b3 +(h-2t)t2)F --- =-------------- 12 12 12252 X5+52X(15-5)2(15x5 + 20x5)(b) =9.643c/??2]41-33 315 53 2 5 203 2J z(9.643 2.5) 15 5 (25 10 9.643) 20 512 123 320 5 5 15 4--------- ------------ 1615cm10186cmJ y12 12求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。
解:y b sin , z cosdy bcos d J zb y2dAb:y2 2zdyJ zb2 22b sin a cos bcos db2ab32sin2cos2 d4ab3i zab34abJ p J z J y(ab3a3b) ab(a2b2)4 4角A 点一对主轴 u 及v 的方位,并求i u及i v1-4 试求图示的£的圆面积(半径a )对于z,4 2 az )dz8I-5图示矩形截面h : b = 3 : 2。

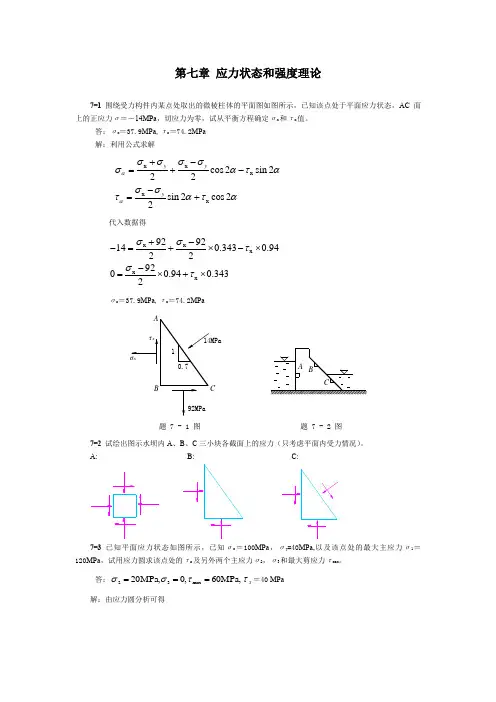
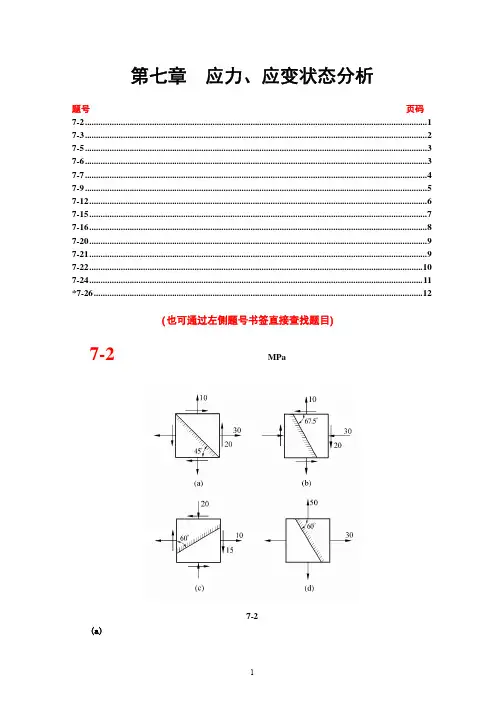
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示,已知该点处于平面应力状态,AC 面上的正应力σ=-14MPa ,切应力为零,试从平衡方程确定σx 和τx 值。
答:σx =37.9MPa ,τx =74.2MPa 解:利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx =37.9MPa ,τx =74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力(只考虑平面内受力情况)。
A: B: C:7-3 已知平面应力状态如图所示,已知σx =100MPa ,σy =40MPa,以及该点处的最大主应力σ1=120MPa ,试用应力圆求该点处的τx 及另外两个主应力σ2,σ3和最大剪应力τmax。
答:MPa,60,0MPa,20max 32===τσσx τ=40 MPa 解:由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ,这些面上还有剪应力,如果最大主应力为拉应力100MPa ,试求:(1) 上述面上的切应力; (2) 此平面上另一主应力; (3) 最大切应力平面上的正应力; (4) 最大切应力。

第7章应力和应变分析强度理论7.1复习笔记一、应力状态一点的应力状态:过一点不同方向面上应力的集合。
应力状态的研究对象是单元体,其特征为:①单元体的尺寸无限小,每个面上应力均匀分布;②任意一对平行平面上的应力相等。
主单元体是指各侧面上切应力均为零的单元体。
其中,单元体上切应力为零的面称为主平面,主平面上的正应力称为主应力。
说明:一点处必定存在一个单元体,使得三个相互垂直的面均为主平面,三个互相垂直的主应力分别记为σ1、σ2、σ3,且规定按代数值大小的顺序来排列,即σ1≥σ2≥σ3。
应力状态分类及实例(1)单向应力状态:也称为简单应力状态,三个主应力σ1、σ2、σ3中只有一个不等于零。
实例:简单的拉伸或压缩。
(2)平面(二向)应力状态:三个主应力σ1、σ2、σ3中有两个不等于零。
实例:薄壁圆筒横截面上的点和圆形容器包含直径的任意横截面上的点。
(3)空间(三向)应力状态:和平面应力状态统称为复杂应力状态,三个主应力σ1、σ2、σ3,均不等于零。
实例:在滚珠轴承中,滚珠与外圈接触点处的应力状态,可以作为三向应力状态的实例。
二、二向应力状态分析1.解析法如图7-1-1(a)所示,一单元体abcd处于平面应力状态,采用截面法取左边部分单元体eaf为研究对象,如图7-1-1(b)所示。
图7-1-1(1)符号规定:由x轴转到外法线n,逆时针转向夹角α为正;正应力仍规定拉应力为正;切应力对单元体内任一点取矩,顺时针转向为正。
(2)应力计算①任意斜截面α上应力正应力:cos2sin222x y x y xy ασσσσσατα+-=+-切应力:sin 2cos 22x y xy ασστατα-=+②主应力主应力的大小2max 2min 22x y x y xy σσσσστσ+-⎛⎫⎫=±+⎬ ⎪⎭⎝⎭将σmax 、σmin 和0按大小顺序排列,分别记为σ1、σ2和σ3。
主平面方位角tan2α0=-2τxy /(σx -σy )约定|α0|<45°,即α0取值在±45°范围内,则确定主平面的规则为:当σx ≥σy 时,α0是σx 与σmax 之间的夹角;当σx <σy 时,α0是σx 与σmin 之间的夹角。
习题8-1构件受力如图所示。
(1)确定危险点的位置; (2)用单元体表示危险点的应力状态。
3M d 3 16(c )A 截面的最上面一点的大小及方位。
解:A1 % ■\ 1 lltt4d2 8-2 图示悬臂粱受载荷 P=20kN 作用,试绘单元体 A 、B 、C 的应力图,并确定主应力 解:(a )在任意横截面上,任意一点■ S -2 ffi解:(a)(b)(c)(d)8-4cos60 13.75MPa -cos 220 10 20 10pcos 1355.606MPa20 10 sin 2—2si n2245;(与1方向夹角)或135「45 (与140方向夹角)单元体各面的应力如图示(应力单位为力的大小及所在截面的方位,并在单元体内注明。
解: (a)(b)(c)(d)8-5135;10.606MPa(与水平方向交角)MPa),试用解析法和图解法计算主应8-3主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力和剪应力,并找出最大剪应力值及方位(应力单位:MPa)。
20方向夹角)145 (与作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
3U解:(a) (b)(c ) (d)(e)8-6出截面上解:已知矩形截面梁某截面上的弯矩和剪力分别为M —10kN • m, F s—120kN,试绘1、2、3、4各点单兀体的应力状态,并求其主应力。
8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC面和BC面上的正应力均为-15MPa,试求AC和BC面上的剪应力与此单元体主应力的大小和方向。
解: X 015MPa1 2 0; 3 30MPa (方向平行于AB)8-8某点的应力状态如图所示,已知、与y,试参考如何根据已知数据直接作出应力图。
8-9 每边均为1cm的钢质立方体,放在边长均为 1.0001cm的刚性方槽内,立方体顶上承受总压力P = 15kN,材料的E= 200GPa, = 0.30。
习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角,梁的抗弯刚度EI 为常量。
7-1(a ) 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ;'0y = 代入上面方程可求得:C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l(b )222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+-3-1=6EJ B ql θ 4-1=8EJB y ql(c )()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++边界条件:0x = 时 0y = ;'0y = 代入上面方程可求得:4024q l C l -= 50120q l D l=()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件:x a = 时 12y y = ;12θθ=代入上面方程可求得:2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤43412476B B qa y EJqa EJθ=-=-(f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件:x a = 时 12y y = ; ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程,端截面转角θA 和θB ,跨度中点的挠度和最大挠度,梁的抗弯刚度EI 为常量。
* *7-2 (a) 解:''0'2030()()26M M xx lM EJy M x x lMEJy x Cl MEJy x Cx Dl====+=++边界条件:0x = 0y = 0D ∴=x l = 0y = 06M lC -∴= 23036M l x x y EJ l l ⎛⎫∴=-- ⎪⎝⎭22'03136M l x y EJ l l θ⎛⎫∴==-- ⎪⎝⎭当'0y =时,可得 3x =;此时挠度最大 2093f EJ =中点挠度 20216M ll y EJ -⎛⎫= ⎪⎝⎭06A M l EJ θ-=03B M lEJθ=(b )解:设中点为C 点,则分析CB 段'''101201301()()26M M x x lM EJy M x x lMEJy x Cl MEJy x Cx Dl====+=++边界条件:0x = 0y = 0D ∴=2l x = 0y = 024M lC -∴=30164M x lx y EJ l ⎛⎫∴=-- ⎪⎝⎭2'0364M x l y EJ l θ⎛⎫∴==-⎪⎝⎭可得最大挠度2f =(x =024A M l EJ θ-=024B M lEJθ-= (c )解:''''02'''03''042'0532'02624212062q EJy x l q x EJy Cl q x EJy Cx Dlq x Cx EJy Dx Al q x Cx Dx EJy Ax Bl ==+=++=+++=++++ 边界条件: 0x = ''00y y =⎧⎨=⎩ x l = ''00y y =⎧⎨=⎩03067360q lC q l A ∴=-= 0D B ==()442203710360q xy x l l x lEJ∴=--- ()'42201530360q y x l x lEJθ==-- 最大挠度: 40153q l f EJ=- (0.5193x l =)307360A q l EJ θ=- 3045B q l EJθ=(d ) 解:()2122''123'11341113()0822()823EJ 823EJ 1663EJ 4824qlx qx l M x x ql l M x l x x l qlx qx y qlx qx y C qlx qx y C x D ⎛⎫=-≤≤ ⎪⎝⎭⎛⎫=-≤≤ ⎪⎝⎭=-=-+=-++()''22'2223222EJ 8EJ 82EJ 826qly l x ql x y lx C ql x x y l C x D =-⎛⎫=-+ ⎪⎝⎭⎛⎫=-++ ⎪⎝⎭边界条件:02x x l == 1120y y y == ; 02x x l == 122''0y y y == 31193840qlC D -== 324117384384ql C qlD -==()()3231322329241603842172483842qx l y l lx x x EJ ql l y l l x lx x x l EJ -⎛⎫=-+≤≤ ⎪⎝⎭-⎛⎫=-+-+≤≤ ⎪⎝⎭4411536ql f EJ= (0.25x l =)4335276831287384A B l ql y EJ ql EJ ql EJθθ⎛⎫=-⎪⎝⎭=-=7-3 已知下列各梁的抗弯刚度EI 为常量,试用初参数法求各梁的挠曲线方程,并计算θC 、y C 、及θD 、y D 。
7-4 计算下列铰接梁在C 处的挠度,设梁的抗弯刚度EI 为常量。
(a)解:CA0M aM23033c M M a a y a EJ EJ=⨯=(b) 解:q()4242233c qaqa y a EJ EJ-=⨯=-(c) 解:DAPP PB'3333333CC D B y y a y Pa Pa Pa EJ EJ EJ Pa EJθ=++⎛⎫⎛⎫---=++ ⎪ ⎪⎝⎭⎝⎭-= (d) 解:()' 33332333103CC E By y a yP a Pa PaEJ EJ EJPaEJθ=++---=---=7-5 门式起重机横梁由4根36a工字钢组成如图所示,梁的两端均可视为铰支,钢的弹性模量E=210Gpa。
试计算当集中载荷P=176 kN作用在跨中并考虑钢梁自重时,跨中截面C的挠度y C。
解:查自重得:4587.02/15760q N mJ cm==3433984985483841761011482101015760104587.0251138521010157601040.0377 3.77Pl qlfEJ EJm cm--=---⨯⨯=⨯⨯⨯⨯⨯-⨯⨯+⨯⨯⨯⨯⨯==7-6 松木桁条的横截面为圆形,跨长为l=4m,两端可视为简支,全跨上作用有集度为q=1.8 kN/m的均布载荷。
已知松木的许用应力[σ]=10MPa,弹性模量E=1.0×103Mpa。
此桁条的容许挠度[y]= l/200,试求此桁条横截面所需的直径。
解:此松木条的最大挠度为45384qlEJ所以:45384200ql lEJ=[]33225 1.82104642000.006179384110321.6898dM qlMPaW dπσσπ⨯⨯⨯⨯=⨯=⨯⨯===<所以取40.0061790.28d m==7-7 试用虚梁法求图示悬臂梁自由端B的Bθ和By。