第一章 习题课(1)
- 格式:doc
- 大小:56.50 KB
- 文档页数:5



概率论与数理统计第一章习题课1. 掷3枚硬币, 求出现3个正面的概率. 解: 设事件A ={出现3个正面}基本事件总数n =23, 有利于A 的基本事件数n A =1, 即A 为一基本事件,则125.08121)(3====n n A P A .2. 10把钥匙中有3把能打开门, 今任取两把, 求能打开门的概率. 解: 设事件A ={能打开门}, 则A 为不能打开门基本事件总数210C n =, 有利于A 的基本事件数27C n A =, 467.0157910212167)(21027==⨯⨯⋅⨯⨯==C C A P因此, 533.0467.01)(1)(=-=-=A P A P .3. 100个产品中有3个次品,任取5个, 求其次品数分别为0,1,2,3的概率.解: 设A i 为取到i 个次品, i =0,1,2,3,基本事件总数5100C n =, 有利于A i 的基本事件数为3,2,1,0,5973==-i C C n i i i则138.09833209495432194959697396979899100543213)(856.0334920314719969798991009394959697)(510049711510059700=⨯⨯⨯=⨯⨯⨯⨯⨯⨯⨯⋅⨯⨯⨯⨯⨯⨯⨯⨯=⨯===⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯⨯⨯===C C n n A P C C n n A P00006.09833512196979697989910054321)(006.0983359532195969739697989910054321)(51002973351003972322=⨯⨯==⨯⨯⋅⨯⨯⨯⨯⨯⨯⨯⨯====⨯⨯=⨯⨯⨯⨯⨯⋅⨯⨯⨯⨯⨯⨯⨯⨯===C C n n A P C C C n n A P4. 一个袋内有5个红球, 3个白球, 2个黑球, 计算任取3个球恰为一红, 一白, 一黑的概率.解: 设A 为任取三个球恰为一红一白一黑的事件,则基本事件总数310C n =, 有利于A 的基本事件数为121315C C C n A =, 则25.0412358910321)(310121315==⨯⨯⨯⨯⨯⨯⨯===C C C C n n A P A5. 两封信随机地投入四个邮筒, 求前两个邮筒内没有信的概率以及第一个邮筒内只有一封信的概率.解: 设A 为前两个邮筒没有信的事件, B 为第一个邮筒内只有一封信的事件,则基本事件总数1644=⨯=n , 有利于A 的基本事件数422=⨯=A n , 有利于B 的基本事件数632=⨯=B n , 则25.041164)(====n n A P A 375.083166)(====n n B P B . 6. 为防止意外, 在矿内同时设有两种报警系统A 与B , 每种系统单独使用时, 其有效的概率系统A 为0.92, 系统B 为0.93, 在A 失灵的条件下, B 有效的概率为0.85, 求(1) 发生意外时, 这两个报警系统至少有一个有效的概率 (2) B 失灵的条件下, A 有效的概率解: 设A 为系统A 有效, B 为系统B 有效, 则根据题意有P (A )=0.92, P (B )=0.93, 85.0)|(=A B P(1) 两个系统至少一个有效的事件为A ∪B , 其对立事件为两个系统都失效, 即B A B A = , 而15.085.01)|(1)|(=-=-=A B P A B P , 则988.0012.01)(1)(012.015.008.015.0)92.01()|()()(=-=-==⨯=⨯-==B A P B A P A B P A P B A P(2) B 失灵条件下A 有效的概率为)|(B A P , 则829.093.01012.01)()(1)|(1)|(=--=-=-=B P B A P B A P B A P 7. 用3个机床加工同一种零件, 零件由各机床加工的概率分别为0.5, 0.3, 0.2, 各机床加工的零件为合格品的概率分别等于0.94, 0.9, 0.95, 求全部产品中的合格率.解: 设A 1,A 2,A 3零件由第1,2,3个机床加工, B 为产品合格,A 1,A 2,A 3构成完备事件组.则根据题意有P (A 1)=0.5, P (A 2)=0.3, P (A 3)=0.2, P (B |A 1)=0.94, P (B |A 2)=0.9, P (B |A 3)=0.95,由全概率公式得全部产品的合格率P (B )为93.095.02.09.03.094.05.0)|()()(31=⨯+⨯+⨯==∑=i i i A B P A P B P8. 12个乒乓球中有9个新的3个旧的, 第一次比赛取出了3个, 用完后放回去, 第二次比赛又取出3个, 求第二次取到的3个球中有2个新球的概率.解: 设A 0,A 1,A 2,A 3为第一次比赛取到了0,1,2,3个新球, A 0,A 1,A 2,A 3构成完备事件组.设B 为第二次取到的3个球中有2个新球. 则有22962156101112321)|(,552132101112789321)(,442152167101112321)|(,55272101112389321)(,552842178101112321)|(,2202710111239321)(,552732189101112321)|(,2201101112321)(312162633123933121527231213292312142813122319131213290312330=⋅⨯⨯⋅⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯⨯⨯⨯===⋅⨯⨯⋅⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯⨯⨯===⋅⨯⨯⋅⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯===⋅⨯⨯⋅⨯⨯⨯⨯===⨯⨯⨯⨯==C C C A B P C C A P C C C A B P C C C A P C C C A B P C C C A P C C C A B P C C A P根据全概率公式有455.01562.02341.00625.00022.022955214421552755282202755272201)|()()(30=+++=⋅+⋅+⋅+⋅==∑=i i i A B P A P B P9. 某商店收进甲厂生产的产品30箱, 乙厂生产的同种产品20箱, 甲厂每箱100个, 废品率为0.06, 乙厂每箱装120个, 废品率是0.05, 求:(1)任取一箱, 从中任取一个为废品的概率;(2)若将所有产品开箱混放, 求任取一个为废品的概率. 解: (1) 设B 为任取一箱, 从中任取一个为废品的事件. 设A 为取到甲厂的箱, 则A 与A 构成完备事件组4.05020)(,6.05030)(====A P A P 05.0)|(,06.0)|(==AB P A B P 056.005.04.006.06.0)|()()|()()(=⨯+⨯=+=A B P A P A B P A P B P(2) 设B 为开箱混放后任取一个为废品的事件.则甲厂产品的总数为30×100=3000个, 其中废品总数为3000×0.06=180个,乙厂产品的总数为20×120=2400个, 其中废品总数为2400×0.05=120个, 因此...055555555.0540030024003000120180)(==++=B P10. 有两个口袋, 甲袋中盛有两个白球, 一个黑球, 乙袋中盛有一个白球两个黑球. 由甲袋中任取一个球放入乙袋, 再从乙袋中取出一个球, 求取到白球的概率.解: 设事件A 为从甲袋中取出的是白球, 则A 为从甲袋中取出的是黑球, A 与A 构成完备事件组. 设事件B 为从乙袋中取到的是白球. 则P (A )=2/3, P (A )=1/3, P (B |A )=2/4=1/2, P (B |A )=1/4, 则根据全概率公式有417.012541312132)|()()|()()(==⨯+⨯=+=A B P A P A B P A P B P11. 上题中若发现从乙袋中取出的是白球, 问从甲袋中取出放入乙袋的球, 黑白哪种颜色可能性大?解: 事件假设如上题, 而现在要求的是在事件B 已经发生条件下, 事件A 和A 发生的条件概率P (A |B )和P (A |B )哪个大, 可以套用贝叶斯公式进行计算, 而计算时分母为P (B )已上题算出为0.417, 因此2.0417.04131)()|()()|(8.0417.02132)()|()()|(=⨯===⨯==B P A B P A P B A P B P A B P A P B A PP (A |B )>P (A |B ), 因此在乙袋取出的是白球的情况下, 甲袋放入乙袋的球是白球的可能性大.12. 假设有3箱同种型号的零件, 里面分别装有50件, 30件和40件, 而一等品分别有20件, 12件及24件. 现在任选一箱从中随机地先后各抽取一个零件(第一次取到的零件不放回). 试求先取出的零件是一等品的概率; 并计算两次都取出一等品的概率.解: 称这三箱分别为甲,乙,丙箱, 假设A 1,A 2,A 3分别为取到甲,乙,丙箱的事件, 则A 1,A 2,A 3构成完备事件组. 易知P (A 1)=P (A 2)=P (A 3)=1/3. 设B 为先取出的是一等品的事件. 则6.04024)|(,4.03012)|(,4.05020)|(321======A B P A B P A B P 根据全概率公式有467.036.04.04.0)|()()(31=++==∑=i i i A B P A P B P 设C 为两次都取到一等品的事件, 则38.039402324)|(1517.029301112)|(1551.049501920)|(240224323021222502201=⨯⨯===⨯⨯===⨯⨯==C C A C P C C A C P C C A C P根据全概率公式有22.033538.01517.01551.0)|()()(31=++==∑=i i i A C P A P C P13. 发报台分别以概率0.6和0.4发出信号“·”和“—”。



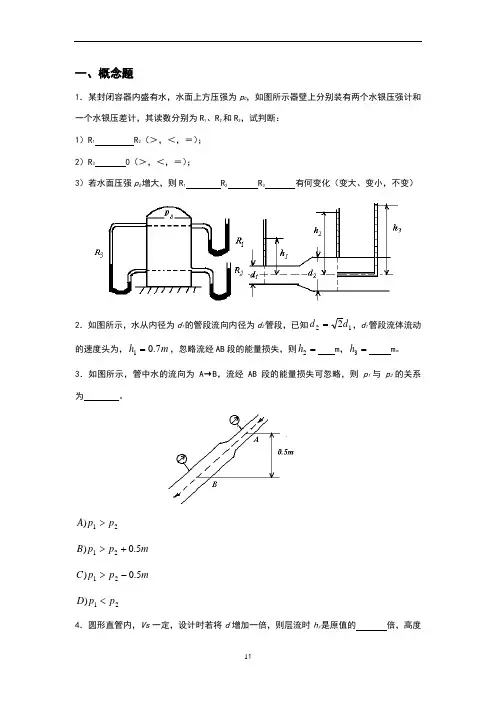
一、概念题1.某封闭容器内盛有水,水面上方压强为p 0,如图所示器壁上分别装有两个水银压强计和一个水银压差计,其读数分别为R 1、R 2和R 3,试判断: 1)R 1 R 2(>,<,=); 2)R 3 0(>,<,=);3)若水面压强p 0增大,则R 1 R 2 R 3 有何变化(变大、变小,不变)2.如图所示,水从内径为d 1的管段流向内径为d 2管段,已知122d d =,d 1管段流体流动的速度头为,m h 7.01=,忽略流经AB 段的能量损失,则=2h m ,=3h m 。
3.如图所示,管中水的流向为A →B ,流经AB 段的能量损失可忽略,则p 1与p 2的关系为 。
21)p p A > m p p B 5.0)21+> m p p C 5.0)21-> 21)p p D <4.圆形直管内,Vs 一定,设计时若将d 增加一倍,则层流时h f 是原值的 倍,高度湍流时,h f 是原值的 倍(忽略管壁相对粗糙度的影响)。
5.某水平直管中,输水时流量为Vs ,今改为输2Vs 的有机物,且水μμ2=,水ρρ5.0=,设两种输液下,流体均处于高度湍流状态,则阻力损失为水的 倍;管路两端压差为水的 倍。
6.已知图示均匀直管管路中输送水,在A 、B 两测压点间装一U 形管压差计,指示液为水银,读数为R (图示为正)。
则: 1)R 0(>,=,<)2)A 、B 两点的压差p ∆= Pa 。
)()ρρ-i Rg A gh Rg B i ρρρ+-)() )()ρρρ--i Rg gh C gh Rg D i ρρρ--)()3)流体流经A 、B 点间的阻力损失f h 为 J/kg 。
4)若将水管水平放置,U 形管压差计仍竖直,则R ,p ∆ ,f h 有何变化7.在垂直安装的水管中,装有水银压差计,管段很短,1,2两点间阻力可近似认为等于阀门阻力,如图所示,试讨论:1)当阀门全开,阀门阻力可忽略时,1p 2p (>,<,=);2)当阀门关小,阀门阻力较大时,1p 2p (>,<,=),R (变大,变小,不变);3)若流量不变,而流向改为向上流动时,则两压力表的读数差p ∆ ,R ;(变大,变小,不变)。



习题课(1)
一、选择题(每小题5分,共30分)
1.若600°角的终边上有一点(-4,a ),则a 的值为( ) A .4 3 B .-4 3 C .±4 3
D. 3
解析:600°角的终边在第三象限,则a <0,故选B. 答案:B
2.cos(-11π
3)的值为( ) A.12 B .-12 C.33
D .-3
2
解析:cos(-11π3)=cos(-4π+π3)=cos π3=1
2. 答案:A
3.若cos θ<0,且sin θ>0,则θ
2是第( )象限角.( ) A .一 B .二
C .一或三
D .任意象限角
解析:由已知cos θ<0,sin θ>0,知θ为第二象限角,即π
2+2k π<θ<π+2k π,k ∈Z ,所以π4+k π<θ2<π2+k π,k ∈Z ,即θ
2为第一或第三象限角.
答案:C
4.已知tan α=-1
2,则1+2sin αcos αsin 2α-cos 2α
的值是( )
A.13 B .3 C .-13
D .-3
解析:原式=sin 2α+cos 2α+2sin αcos α
sin 2α-cos 2α
=tan 2α+1+2tan αtan 2α-1
=1
4+1-1
14-1=-13. 答案:C
5.设a =sin 5π7,b =cos 2π7,c =tan 9π
7,则( ) A .a <b <c B .a <c <b C .b <c <a
D .b <a <c
解析:∵a =sin 5π7=sin 2π7,c =tan 9π7=tan 2π
7, 由角2π
7的三角函数线,
可知cos 2π7<sin 2π7<tan 2π
7,即b <a <c . 答案:D
6.已知cos(5π12+α)=13,且-π<α<-π2,则cos(π
12-α)等于( ) A.233 B.13 C .-13
D .-223
解析:cos(π12-α)=cos[π2-(5π
12+α)] =sin(5π
12+α).
又-π<α<-π
2, ∴-712π<5π12+α<-π12. ∴sin(512π+α)=-223. ∴cos(π12-α)=-223. 答案:D
二、填空题(每小题5分,共15分)
7.已知α为第三象限角,且tan α=2,则cos α=________. 解析:∵sin α=2cos α,
∴4cos 2α+cos 2α=1,即cos 2α=1
5, 又∵α为第三象限角,∴cos α=-5
5. 答案:-5
5
8.若角α终边落在直线x +y =0上,则sin α
1-sin 2α+1-cos 2αcos α的值为________.
解析:原式=sin α|cos α|+|sin α|
cos α,当α为第二、四象限角时,去掉绝对值号可得结果为0.
答案:0
9.已知A =sin (k π+α)sin α+cos (k π+α)
cos α(k ∈Z ),则A 的值构成的集合是________.
解析:当k =2n ,n ∈Z 时,
A =sin (2n π+α)sin α+cos (2n π+α)cos α =sin αsin α+cos αcos α=2. 当k =2n +1,n ∈Z 时,
A =sin[(2n +1)π+α]sin α+cos[(2n +1)π+α]cos α =-sin αsin α+-cos α
cos α=-2.
∴A 的值构成的集合是{2,-2}. 答案:{2,-2} 三、解答题(共45分)
10.(本小题15分)已知(tan α-3)(sin α+cos α+3)=0.求下列各式的值.
(1)4sin α-2cos α5cos α+3sin α;(2)23sin 2α+14cos 2α. 解:由已知tan α-3=0,即tan α=3. (1)原式=4tan α-25+3tan α=4×3-25+3×3=1014=5
7.
(2)原式=23sin 2α+14cos 2αsin 2α+cos 2α=23tan 2α+14
tan 2α+1
=23×9+1
49+1
=58.
11.(本小题15分)已知方程2x 2-(3+1)x +m =0的两根分别为sin θ,cos θ.求实数m 的值.
解:由根与系数的关系,得sin θ+cos θ=3+12,sin θcos θ=m 2,
∴(sin θ+cos θ)2
=(3+12)2
,
即1+2sin θcos θ=2+3
2.
∴sin θcos θ=34,∴m 2=34,∴m =3
2. 12.(本小题15分)已知f (n )=sin n π
4,n ∈Z .
(1)求证:f (1)+f (2)+…+f (8)=f (9)+f (10)+…+f (16); (2)求f (1)+f (2)+…+f (2003). 解:(1)证明:f (1)+f (2)+…+f (8) =sin π4+sin 2π4+sin 3π4+…+sin 7π4+sin 8π4 =22+1+22+0-22+…-2
2+0=0. 同理f (9)+f (10)+…+f (16)=0.
∴f (1)+f (2)+…+f (8)=f (9)+f (10)+…+f (16).
(2)由(1)可知,从第一项开始,每8项的和为0,又2003=250×8+3
∴f (1)+f (2)+…+f (2003)
=250×0+f (2001)+f (2002)+f (2003) =sin 20014π+sin 20024π+sin 20034π =sin π4+sin 2π4+sin 3π
4=2+1.。