方格网法计算场地平整土方量!

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种。

(1)方格网法用于地形较平缓或台阶宽度较大的地段。

计算方法较为复杂，但精度较高，其计算步骤和方法如下：1)划分方格网根据已有地形图(一般用1：500的地形图)将欲计算场地划分成若干个方格网,尽量与测量的纵、横坐标网对应，方格一般采用20m×20m或40m×40m,将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度(挖或填)，填在方格网的左上角,挖方为（－），填方为（＋）。

2）计算零点位置在一个方格网内同时有填方或挖方时,应先算出方格网边上的零点的位置，并标注于方格网上,连接零点即得填方区与挖方区的分界线（即零线）。

零点的位置按下式计算（图6—3）：（6—8）式中x1、x2——角点至零点的距离（m）；h1、h2——相邻两角点的施工高度（m），均用绝对值；a-—方格网的边长（m）。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置,如图6-4所示，方法是用尺在各角上标出相应比例，用尺相接,与方格相交点即为零点位置.这种方法可避免计算(或查表）出现的错误。

3）计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量,或用查表法计算,有关计算用表见表6—31.常用方格网点计算公式表6-31注:1.a——方格网的边长（m)；b、c——零点到一角的边长（m）；h1、h2、h3、h4——方格网四角点的施工高程（m)，用绝对值代入;Σh—-填方或挖方施工高程的总和(m），用绝对值代入;V--挖方或填方体积（m3)。

2。

本表公式是按各计算图形底面积乘以平均施工高程而得出的。

4）计算土方总量将挖方区（或填方区)所有方格计算土方量汇总，即得该场地挖方和填方的总土方量.[例6-1] 厂房场地平整,部分方格网如图6-5所示,方格边长为20m×20m，试计算挖填总土方工程量。

如何计算场地平整土方工程量(总3页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除如何计算场地平整土方工程量土方, 工程量, 平整在场地平整土方工程施工之前，通常要计算土方的工程量。

但土方外形往往复杂，不规则，要得到精确的计算结果很困难。

一般情况下，可以按方格网将其划为一定的几何形状，并采用具有一定精度而又和实际情况近似的方法进行计算。

场地平整土方量的计算可按以下步骤进行：①场地设计标高确定后，求出平整的场地方格网各角点的施工高度Hi②确定“零线”的位置。

确定“零线”的位置有助于了解整个场地的挖、填区域分布状态。

③然后按每个方格角点的施工高度算出填、挖土方量，并计算场地边坡的土方量，这样即得到整个场地的填、挖土方总量。

1。

确定方格网零线及零点零线即挖方区与填方区的交线，在该线上，施工高度为零。

零线的确定方法是：在相邻角点施工高度为一挖一填的方格边线上，用插入法求出方格边线上零点的位置（图1-4），再将各相邻的零点连接起来即得零线。

此主题相关图片如下：001.gif如不需计算零线的确切位置，则绘出零线的大致走向即可。

绘出例1-1计算结果的零线位置。

解:先将各点的施工高度标在图上,然后查找相邻角点为一挖一填的方格边线。

本题共有a2-3、a6-7、a13-14、a18-19、a21-22、a5-10、a6-11、a2-7、a17-22、a18-23、a9-14这些边线。

用插入法求各方格边线零点位置x=8.56ma2-3：此主题相关图片如下：002.gifx=8.56ma2-7：此主题相关图片如下：003.gifx=9.72ma6-7：此主题相关图片如下：004.gifx=0.54m其余零点位置见例1-4图.连接各零点得到零线.2。

土方工程量计算零线确定后，便可进行土方量的计算。

方格中土方量的计算有两种方法：“四方棱柱体法”和“三角棱柱体法”。

这个图是施工单位进场后在基础开挖以前，由测量员或技术员对施工现场的自然地坪进行测量.先按矩型排点,排完以后点之间连上线就像百格网,横竖按一定距离分布测量点，一般根据场地大小设定（5米20米不等）,测量标高，在百格网上标明标高数据。

绘制完成以后报监理或甲方验证签字，这个文件就是百格网。

它的主要用途就是确定土方的挖填工程量，以便于施工统计和结算。

土石方调配施工及计算问题：1，对于大面积土石方开挖,可采用方格网法，根据各点标高计算处土方工程的零线，根据零线可调配各个方格区域内挖填的土方，根据总量可计算出土方是否需要借土还是外弃。

当然，要注意土方要乘松散系数，比如挖1.09m3填1m3. 2，对于道路上的土石方，在设计图里有道路工程那一册，里面便有土石方调配平衡表，道路工程一般为1km内土石方平衡利用，超过1km需计算运距或者外借土.计算方法可采用纵断面的调配示意图来表示。

按1km一个区间进行调配。

主要依据:1，原始测量数据，原地面标高与开挖后标高；2,方格网平面图；3，设计图内的土石方平衡调配表;4，计算表;5，土石方计算规则，比如考虑松散系数等2．场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种。

(1）方格网法用于地形较平缓或台阶宽度较大的地段.计算方法较为复杂，但精度较高，其计算步骤和方法如下：1)划分方格网根据已有地形图（一般用1：500的地形图）将欲计算场地划分成若干个方格网，尽量与测量的纵、横坐标网对应，方格一般采用20m×20m或40m×40m，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填），填在方格网的左上角，挖方为（－），填方为（＋）。

2）计算零点位置在一个方格网内同时有填方或挖方时,应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界线(即零线)。

场地平整土方量计算方法分析作者：李卓松来源：《城市建设理论研究》2013年第17期摘要:在对场地平整土方量计算时，方格网法是最为常用的土方量计算方法之一，本文从方格网法出发，阐述场地平整土方量计算方法。

关键词:场地平整；方格网法；计算方法；土方量中图分类号： V552 文献标识码： A 文章编号：引言在土地开发整理以及建筑场地平整土石方施工工程中，方格网法是一种最简单同时也是最为实用的计算方法之一。

这些工程中的土石方量的计算是否精准，直接关系到工程施工成本，如若出现偏差将导致工程成本的增加，因此在进行土方量计算的过程中，需要掌握好相关的计算方法，确保计算的精准性。

1、方格网法计算土方量的原理方格网法是土方量计算的基本方法,很大部分的场地平整土方量计算仍然基于方格网法计算原理进行手工、半手工或计算机软件计算,且很大部分土方计算软件在数字高程模型建模时仍然使用基于格网的表面建模。

它的基本原理是:在需要计算的范围内按一定的间距绘好方格网,以设计高程面作为土方计算底面,根据地形图上高程点或等高线内插出各方格顶点的高程,分别计算出各方格的土方量,然后将全部方格内土方量累加起来得到总土方量。

方格网法通常适用于平坦及高差不太大、地形比较平缓的地区。

方格网法的基本原理是将要平整的项目区场地,根据地形复杂程度、地形图比例尺以及精度要求划分成边长为10m~50m 的方格,在水平面上形成方格网,分别测出各方格网4个顶点的高程,根据地面高程和设计高程计算各个格网挖填深度及土方量,最后汇总格网挖填土方量和边坡土方量,即为场地平整总土方量。

2、计算方法及改进方格网法计算公式很多，用不同的计算公式，工作方案和程序便不一样。

一般用水准测量或三角高程测量方法，测出方格网点的标高，计算方格网的平均标高H及面积S，平均标高H 平均可按下述几种方法计算:1)算术平均法。

将格网的4个角点高程相加求和，除以点的总数即为平均标高。

2)加权平均法。

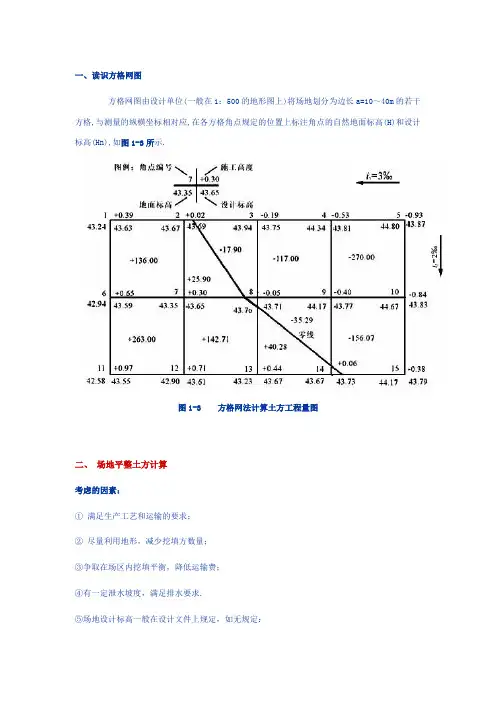
一、读识方格网图方格网图由设计单位(一般在1：500的地形图上)将场地划分为边长a=10～40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图1-3所示.图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素：① 满足生产工艺和运输的要求；② 尽量利用地形，减少挖填方数量；③争取在场区内挖填平衡，降低运输费；④有一定泄水坡度，满足排水要求.⑤场地设计标高一般在设计文件上规定，如无规定：A.小型场地――挖填平衡法；B.大型场地――最佳平面设计法(用最小二乘法，使挖填平衡且总土方量最小)。

1、初步标高(按挖填平衡)，也就是设计标高。

如果已知设计标高，1.2步可跳过。

场地初步标高：H0=(∑H1+2∑H2+3∑H3+4∑H4)/4MH1－－一个方格所仅有角点的标高；H2、H3、H4－－分别为两个、三个、四个方格共用角点的标高.M——方格个数.2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整.按泄水坡度调整各角点设计标高：①单向排水时，各方格角点设计标高为: Hn = H0 ±Li②双向排水时，各方格角点设计标高为：Hn = H0± Lx ix± L yi y3.计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差，是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算：式中hn------角点施工高度即填挖高度(以“+”为填，“-”为挖)，m；n------方格的角点编号(自然数列1，2，3，…，n).Hn------角点设计高程，H------角点原地面高程.4.计算“零点”位置，确定零线方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点，即“零点”(如图1-4所示).图1-4 零点位置零点位置按下式计算：式中x1、x2 ——角点至零点的距离,m；h1、h2 ——相邻两角点的施工高度(均用绝对值),m；a —方格网的边长，m.5.计算方格土方工程量按方格底面积图形和表1-3所列计算公式，逐格计算每个方格内的挖方量或填方量.表1-3 常用方格网点计算公式6.边坡土方量计算场地的挖方区和填方区的边沿都需要做成边坡,以保证挖方土壁和填方区的稳定。

土方量计算方法现在说到土方量结算，绝大多数施工行业的人都说某某软件很方便，但是我要问到手算会吗，大多数人都会支支吾吾，虽然手算确实不现实，但是我们做为专业人员，总不能沦为软件使用者吧？其中的原理大家还是需要明白的。

今天就给大家讲讲土方量手算，学校交给我们的方法。

一、土方量计算方格网法计算场地平整土方量步骤如图1-1所示。

图1-1 方格网法计算场地平整土方量步骤（一）读识方格网图图1-2 方格网法计算土方工程量图（二）确定场地设计标高1．确定场地设计标高需要考虑的因素（1）满足生产工艺和运输的要求。

（2）尽量利用地形，减少挖填方数量。

（3）争取在场区内挖填平衡，降低运输费。

（4）有一定泄水坡度，满足排水要求。

2．初步计算场地设计标高（按挖填平衡）计算的场地设计标高：式中，H1、H2、H3、H4分别为一个方格、两个方格、三个方格、四个方格共用角点的标高（m），如图1-3b所示。

（三）场地各方格角点的施工高度的计算施工高度为场地各方格角点设计地面标高与自然地面标高之差，是以角点设计标高为基准的挖方或填方的施工高度。

各方格角点的施工高度按下式计算：式中，hn为各角点的施工高度，即填挖高度（以“+”为填，“-”为挖）（m）；n为方格的角点编号（自然数列1，2，3，…，n）；Hn为角点的设计标高（m），若无泄水坡时，即为场地的设计标高（m）；H为角点原地面标高（m）。

（四）计算“零点”位置，确定“零线”方格边线一端施工标高为“+”，若另一端为“-”，则沿其边线必然有一处不挖不填的点，即“零点”，如图1-5所示。

零点位置按下式计算：式中，x1、x2为角点至零点的距离（m）；h1、h2为相邻两角点的施工高度（均用绝对值）（m）；a为方格网的边长（m）。

（五）计算方格土方工程量的计算1．方格的4个角点全为填方或挖方方格的4个角点全为填方或挖方，如图1-7所示。

其计算公式如下：2 . 两个点填方，两个点挖方方格的相邻两个角点为填方，另外两个点为挖方，如图1-8所示。

方格网土方计算公式
11.2.1 方格网法土方计算
方格网法土方计算适用于地形变化比较平缓的地形情况，用于计算场地平整的土方量计算较为精确。

具体做法如下:
首先建立地形的坐标方格网，方格网的一边与地形等高线或场地坐标网平行，大小根据地形变化的复杂程序和设计要求的精度确定，边长一般常采用20m×20m 或40m×40m(地形平坦、机械化施工时也可采用100m×100m)。

然后求出方格各个角点的自然标高、设计标高以及施工高程。

计算零点位置，在每相邻的填方点和挖方点之间总存在一个零点，零点的确定方法如下:
说明:
X:零点据填方角顶的距离;X:零点据挖方角顶的距离 tw
h:填方高度;h:挖方高度;a:方格边长 tw
连接每个方格上的相邻两个零点，根据零线将方格划分的情况，采用相应公式来计算，如表 11-2所示。

汇总，分别将填方区、挖方区所有土方汇总，得到填、挖土方总量。

四个角点全填方(或全挖方)
一个角点填方(或挖方)，另外三个角点挖方(或填方)
一侧两个角点填方(或挖方)，另一侧两个角点挖方(或填方)
相对两个角点填方(或挖方)，另外相对两个角点挖方(或填方)
表 11-2 方格网法土方计算公式说明:
a:方格边长(m)
h、h、h、h:方格网角点的施工高度，正值代表填方，负值代表挖方 12343V、V-:填方(或挖方)的体积(m) +。

场地平整土方量计算的步骤和方法说实话场地平整土方量计算这事儿，我一开始也是瞎摸索。

我试过好多种方法，也走了不少弯路呢。

首先我想说方格网法，这是我最早接触的方法。

就是把场地划分成一个个小方格，就像棋盘那样。

我最开始总是弄错方格的大小，我想着方格大一点不就计算简单嘛，结果大错特错。

方格大了，地形起伏的细节就被忽略了，算出来的土方量偏差特别大。

后来我才知道方格大小得根据场地的大小和地形复杂程度来定，一般的场地如果地形有点复杂的话，5米乘5米或者10米乘10米这样的方格就比较合适。

然后要测量每个方格角点的原地形标高。

这可不容易，刚开始我拿着水准仪在那测，测着测着就晕了，不知道哪些点测过哪些没测。

这里就一定要有条理，最好先画个简单的示意图，把方格角点编号，一个一个按顺序测，就像按图索骥一样。

接着算出土方挖填高度，每个方格角点的设计标高减去原地形标高就是了。

这里我犯过的错误就是对设计标高没理解透，以为设计师给的标高是个固定不变的数，其实还得考虑排水坡度之类的因素。

之后将每个方格的挖填土方量计算出来，再汇总，这个过程就是个细活，要特别仔细。

再就是断面法。

我觉得这种方法就像是把场地横着切成一片片来看。

先确定断面的间距，我当初是没有什么概念就随便定，后面发现合适的间距能让计算结果更准确。

这个要多根据场地的长度来调整，短一点的场地间距可以小点，长的场地就稍大点，差不多20米到50米这样，具体还得看实际地形状况。

测量断面的原地形和设计地形特征点标高的时候也很关键，就跟方格网法测量角点标高一样容不得马虎。

计算每个断面的挖填方面积，这步骤就像是算一个特殊形状的面积似的，有点复杂，不过可以把它分成几个规则形状来算。

最后用断面面积算出各段的土方量，再累加起来。

场地平整土方量计算真不是个简单事儿，得慢慢摸索，多实践，总结自己犯过的错，这样才能把土方量计算得准确点。

还有就是如果有新方法出现或者有软件可以辅助计算的，也可以去尝试尝试，说不定能省不少事儿。

方格网法土方量计算的计算原理和方法文章类别：工程论文摘要：下文分析了方格网法进行土石方量计算的使用原理，提出了一种适用于平整场地后地面不为平面的工程土方量的计算方法。

关键词：土方量计算，方格网法，计算方法，原理1引言土方量计算方法有许多种，目前我们比较常用的有断面法、DTM法、等高线法和方格网法等4种土方量计算方法。

断面法、DTM法、和等高线方法只适于基准面为平面的土方量的计算，对于基准面为斜面或不规则形状，则不能直接应用上述方法。

对这种情况，可假设一个共同的基准面，计算场地平整前后相对于该基准面的填挖方量，两次填挖方量的差就是所要求的填挖方量。

下面就方格网法土方量计算的计算原理和方法进行阐述。

2方格网法当建筑场地规整、地形较为平坦，场地设计标高尚未确定或已经确定时，均可以采用方格网法进行土方计算。

该方法首先将场地划分为若干方格(一般为边长5～20m的正方形)，从地形图或实测得到每个方格角点的自然标高，由给出的地面设计标高，根据各点的设计标高与自然标高之差，求出零线位置，进而求出各方格的工程量，所有方格的工程量之和即为整个场地的工程量。

2．1方格网四角原始高程数据的计算从原始地形图中直接剖取，可按地形图上的等高线用内插法求得或采用就近原则进行剖取计算。

把测区的地形表面按一定的格网间距dx、dy(一般dx=dy)进行格网化，然后求出每个方格中心点的高程作为该方格面元的平均高程，最后按一定排列(如按行或列)进行存储，从而得到基于规则格网的面元DTM。

2．2方格网四角设计高程的计算量算方格点的地面高程，注在相应方格点的右上方。

为使挖方与填方大致平衡，可取各方体积点高程的平均值作为设计高程H0，则各方格点的施工标高hi为：hi=H0-Hi将施工标高注在地面高程的下面，负号表示挖土，正号表示填土。

在图上按设计高程确定填挖边界线，根据方格四个角点的施工标高符号不同。

可选择以下四种情况之一，计算各方格的填挖方量。

补充：方格网法计算土方工程量在进行土方工程量计算之前，将绘有等高线的现场地形图，分为若干数量的方格（或根据测绘的方格网图），然后按设计高程和自然高程，求出挖填高程，进行土方量的计算。

适用于地形平缓或台阶宽度较大的地段采用。

其计算步骤为：1、方格的划分常用的方法是在1/500的地形图上，以20×20或40×40m 划分成若干个方格，将设计标高和地面标高分别标在方格点的右上角和右下角，将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填），填在方格网的左上角，挖方为（+）填方为(-)。

2、计算零点位置：在一个方格网内同时有填方或挖方时，要先算出方格边的零点位置，并标注于方格网上，连按零点就得零线，它是填方区与挖方区的分界线。

零点的位置按下式计算：a h h h ⨯+=2111χ a h h h ⨯+=2122χ 式中、—角点至零点的距离（m ）、—相邻两角点的施工高度（m ）均用绝对值—方格网的边长（m ）在实际工作中，为省略计算，常采用图解法直接求出零点。

方法是用尺在各角上标出相应比例，用尺相连，与方格相交点即为零点位置。

3、计算土方工程量按方格网底面积图形和表7-10所列公式计算每个方格法内的挖方或填方量或用查表法计算。

4、计算土方总量将挖方区（或填方区）所有方格计算土方量汇总，即得到该场地挖方和填方的总土方量。

例：某建筑场地方格网的一部分如图所示，方格边长为20×20m ，试用公式法计算挖填土方总量。

解：（1）划分方格网计算方格各点的施工高度（2）计算零点位置：从图7-3（b ）中知，8~13，9~14，14~15三条方格边两端的施工高度符号不同，说明在此方格边上有零点存在。

a h h h ⨯+=2111χ 8-13线)(6.72026.016.016.01m =⨯+=χ9-14线)(0.112021.026.026.01m =⨯+=χ 14-15线)(2.162005.021.021.01m =⨯+=χ 将各零点标于图上，并将零点线连接起来。

一、读识方格网图方格网图由设计单位(一般在1：500的地形图上)将场地划分为边长a=10～40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图1-3所示.图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素：① 满足生产工艺和运输的要求；② 尽量利用地形，减少挖填方数量；③争取在场区挖填平衡，降低运输费；④有一定泄水坡度，满足排水要求.⑤场地设计标高一般在设计文件上规定，如无规定：A.小型场地――挖填平衡法；B.大型场地――最正确平面设计法(用最小二乘法，使挖填平衡且总土方量最小)。

1、初步标高(按挖填平衡)，也就是设计标高。

如果已知设计标高，1.2步可跳过。

场地初步标高：H0=(∑H1+2∑H2+3∑H3+4∑H4)/4MH1－－一个方格所仅有角点的标高；H2、H3、H4－－分别为两个、三个、四个方格共用角点的标高.M——方格个数.2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整.按泄水坡度调整各角点设计标高：①单向排水时，各方格角点设计标高为: Hn = H0 ±Li②双向排水时，各方格角点设计标高为：Hn = H0± Lx ix± L yi y3.计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差，是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算：式中hn------角点施工高度即填挖高度(以“+”为填，“-”为挖)，m；n------方格的角点编号(自然数列1，2，3，…，n).Hn------角点设计高程，H------角点原地面高程.4.计算“零点”位置，确定零线方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点，即“零点”(如图1-4所示).图1-4 零点位置零点位置按下式计算：式中x1、x2 ——角点至零点的距离,m；h1、h2 ——相邻两角点的施工高度(均用绝对值),m；a —方格网的边长，m.5.计算方格土方工程量按方格底面积图形和表1-3所列计算公式，逐格计算每个方格的挖方量或填方量.表1-3 常用方格网点计算公式6.边坡土方量计算场地的挖方区和填方区的边沿都需要做成边坡,以保证挖方土壁和填方区的稳定。

一、读识方格网图方格网图由设计单位(一般在1：500的地形图上)将场地划分为边长a=10～40m的若干方格,与测量的纵横坐标相对应，在各方格角点规定的位置上标注角点的自然地面标高（H）和设计标高(Hn),如图1—3所示。

图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素:① 满足生产工艺和运输的要求；② 尽量利用地形，减少挖填方数量;③争取在场区内挖填平衡，降低运输费;④有一定泄水坡度，满足排水要求.⑤场地设计标高一般在设计文件上规定,如无规定：A.小型场地――挖填平衡法；B。

大型场地――最佳平面设计法（用最小二乘法，使挖填平衡且总土方量最小)。

1、初步标高（按挖填平衡）,也就是设计标高。

如果已知设计标高,1.2步可跳过.场地初步标高:H0=（∑H1+2∑H2+3∑H3+4∑H4）/4MH1－－一个方格所仅有角点的标高；H2、H3、H4－－分别为两个、三个、四个方格共用角点的标高。

M -—方格个数.2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整.按泄水坡度调整各角点设计标高：①单向排水时，各方格角点设计标高为: Hn = H0 ±Li②双向排水时，各方格角点设计标高为：Hn = H0± Lx ix± L yi y3。

计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差,是以角点设计标高为基准的挖方或填方的施工高度。

各方格角点的施工高度按下式计算：式中hn-————-角点施工高度即填挖高度（以“+”为填，“-”为挖),m；n—-——-—方格的角点编号(自然数列1，2，3，…，n)。

Hn—-—--—角点设计高程，H——————角点原地面高程。

4。

计算“零点”位置，确定零线方格边线一端施工高程为“+”,若另一端为“—"，则沿其边线必然有一不挖不填的点，即“零点”（如图1-4所示).图1—4 零点位置零点位置按下式计算：式中x1、x2 ——角点至零点的距离，m；h1、h2 ——相邻两角点的施工高度(均用绝对值）,m；a —方格网的边长，m。

一、读识方格网图方格网图由设计单位(一般在1：500的地形图上)将场地划分为边长a=10～40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图1-3所示.图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素：① 满足生产工艺和运输的要求；② 尽量利用地形，减少挖填方数量；③争取在场区内挖填平衡，降低运输费；④有一定泄水坡度，满足排水要求.⑤场地设计标高一般在设计文件上规定，如无规定：A.小型场地――挖填平衡法；B.大型场地――最佳平面设计法(用最小二乘法，使挖填平衡且总土方量最小)。

1、初步标高(按挖填平衡)，也就是设计标高。

如果已知设计标高，1.2步可跳过。

场地初步标高：H0=(∑H1+2∑H2+3∑H3+4∑H4)/(4*M)H1－－一个方格所仅有角点的标高；H2、H3、H4－－分别为两个、三个、四个方格共用角点的标高.M ——方格个数.2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整.按泄水坡度调整各角点设计标高：①单向排水时，各方格角点设计标高为:Hn = H0 ±Li②双向排水时，各方格角点设计标高为：Hn = H0±Lx ix±L yi y3.计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差，是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算：式中hn------角点施工高度即填挖高度(以“+”为填，“-”为挖)，m；n------方格的角点编号(自然数列1，2，3，…，n).Hn------角点设计高程，H------角点原地面高程.4.计算“零点”位置，确定零线方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点，即“零点”(如图1-4所示).图1-4 零点位置零点位置按下式计算：式中x1、x2 ——角点至零点的距离,m；h1、h2 ——相邻两角点的施工高度(均用绝对值),m；a —方格网的边长，m.5.计算方格土方工程量按方格底面积图形和表1-3所列计算公式，逐格计算每个方格内的挖方量或填方量.表1-3 常用方格网点计算公式6.边坡土方量计算场地的挖方区和填方区的边沿都需要做成边坡,以保证挖方土壁和填方区的稳定。

场地平整的土方量计算场地平整前，要确定场地设计标高，计算挖填土方量以便据此进行土方挖填平衡计算，确定平衡调配方案，并根据工程规模、施工期限、现场机械设备条件，选用土方机械，拟定施工方案。

1．场地平整高度的计算对较大面积的场地平整，正确地选择场地平整高度（设计标高），对节约工程投资、加快建设速度均具有重要意义。

一般选择原则是：在符合生产工艺和运输的条件下，尽量利用地形，以减少挖方数量；场地内的挖方与填方量应尽可能达到互相平衡，以降低土方运输费用；同时应考虑最高洪水位的影响等。

场地平整高度计算常用的方法为“挖填土方量平衡法”，因其概念直观，计算简便，精度能满足工程要求，应用最为广泛，其计算步骤和方法如下：（1)计算场地设计标高如图6-2（a），将地形图划分方格网（或利用地形图的方格网），每个方格的角点标高，一般可根据地形图上相邻两等高线的标高，用插入法求得。

当无地形图时，亦可在现场打设木桩定好方格网，然后用仪器直接测出。

图6-2场地设计标高计算简图（a）地形图上划分方格；（b)设计标高示意图1-等高线；2-自然地坪；3-设计标高平面；4-自然地面与设计标高平面的交线（零线）一般要求是，使场地内的土方在平整前和平整后相等而达到挖方和填方量平衡，如图6-2（b）。

设达到挖填平衡的场地平整标高为H0，则由挖填平衡条件，H 0值可由下式求得：N H H H H H 443243210∑∑∑∑+++= （6-5)式中 a ——方格网边长（m ）；N ——方格网数（个）；H 11…H 22——任一方格的四个角点的标高（m ）；H 1——一个方格共有的角点标高（m ）；H 2——二个方格共有的角点标高（m ）；H 3——三个方格共有的角点标高（m ）；H 4——四个方格共有的角点标高（m ）。

(2）考虑设计标高的调整值上式计算的H 0，为一理论数值，实际尚需考虑：1)土的可松性；2)设计标高以下各种填方工程用土量，或设计标高以上的各种挖方工程量；3)边坡填挖土方量不等；4)部分挖方就近弃土于场外，或部分填方就近从场外取土等因素。