高斯函数问题赏析

以”高斯函数”为背景的问题中蕴含的数学思想分析作者：家辉培优数学老师——陈怡[]x 表示不超过x 的最大整数,比如[2.4]2,[ 1.3]2=-=-,把函数[]y x =称为高斯函数,又称为取整函数. 在高中数学的各知识点中,频繁出现以高斯函数为背景的问题,高斯函数也是高考和竞赛的热门素材,它形式新颖，解答巧妙，能考察学生的数学素养和潜能.本篇文章通过列举一些高斯函数与高中数学各个知识点相结合的问题,在分析并解决这些问题过程中，最后总结背后蕴含数学思想. 一、不等式思想与高斯函数取整符号[]x 本身就蕴含不等式[][]11x x x x -<≤<+，因此在处理一些高斯函数方程问题的时候，可以构造出不等式，通过解不等式的解集确定方程可能的范围.然后逐一带入验证得到方程的解.例1、设[]m 表示不超过实数m 的最大整数，则集合2{|930[]200}x R x x ∈-+=中所有元素的和为 .解析：由2930[]200()x x -+=*，得230[]9200x x =+>，则[]1,x ≥ 从而 1.x ≥因为[],x x ≤ 所以22[].x x ≤ 所以，29[]30[]200,x x -+≤ 即2(3[]5) 5.x -≤所以[]1[]2x x ==或.若[]1x =，代入得13x =；若[]2,x =带入得23x =.例2、若a 为正数，[]a 表示不超过a 的整数部分，{}[],a a a =-如果[]{}a a a 、、顺次组成等比数列，则a = .解析：由题意得，2[]{}a a a =⋅即2[]([])a a a a =-整理得：22[][]()a a a a =+*，因为[]1a a >-，得到22(1)(1)a a a a >-+- 即2310,a a -+<解得3(0,2a ∈.所以，[]1 2.a =或 当[]1,a =代入()*得：a =符合要求；当[]2a =，代入()*得1a =+不符合题意.因此，a =点评：解带有高斯函数的方程，一般先要确定[]x 的范围，然后再一一代入原方程求解.如何求解[]x 的范围，例题1给出两种不同的方法.首先是230[]9200x x =+>，通过这个不等式可以得到[]x 的范围;再有[],x x ≤然后得到29[]30[]200,x x -+≤这是一种基于[]x 本身的范围，通过放缩得到的一个不等式.例题2通过[]1a a >-先确定了a 范围，再得到[]a 的范围.总结方法，通过问题外部的不等式结构和本身的不等式得到关于x 或者[]x 的范围,得到[]x 的范围，再代入计算.这里主要体现了体现了不等式的思想. 2 、分组思想与高斯函数要计算1011[]3k k =∑的值，需要分3,31,32n k n k n k ==+=+讨论，当n 取这三个值[]3nk =,因此把n 取这三个数分为一组进行分组计算33033132[][][]333k k k k =++++∑=3331683k k ==∑.有些分组问题需要一定的技巧，比如当,,x y Z x y Z +∈∉,[][][] 1.x y x y +=+-这个性质在计算取整问题中(例4)显得特别有用.例3、符号[]x 表示不超过x 的最大整数，n 是正整数，则20141([][][])236n n n n=++=∑ . 解析：设()[][][]236n n n f n =++，任意k N ∈，666(6)[][][]6,236k k kf k k =++=616161(61)[][][]6,236k k k f k k ++++=++=同理可得：(62)61,f k k +=+(63)62,f k k +=+(64)63,f k k +=+(65)63,f k k +=+所以，20141([][][])236n n n n=++=∑2014([][][])236n n n n=++=∑335((6)(61)(62)k f k f k f k =++++∑(63)(64)(65))(2015)f k f k f k f ++++++-=335(369)(63355)k k f =+-⨯+∑=2027091点评：这里对n 以6的余数分了6类，这样的分类能使得[],[],[]236nn n 都能求出来，这里的6是2,3,6的最小公倍数.在计算的过程中，注意到0k =时(0)0f =，再以六为循环进行计算.这里体现了分类讨论以及分组求和的思想.例4、设89nn a =，则1232014[][][][]S a a a a =++++=.（符号[]x 表示不超过x的最大正整数）解析: 对任意的212k k a a -、均不是整数，且2122121288899k kk k k a a ---+=+=. 所以对任意的正整数,k 21212[][]81k k k a a --+=-.所以100710071007100721212118(164)8(641)[][]8116463k k k k k S a a --==--=+=-==-∑∑-1007.点评：本题的突破点在于以下事实：Z x y +∈，且,x y Z ∉，则[]1x y x y +=+-.发现了这个性质之后，用分组求和的方法即可.接下来，我们解决一个稍复杂的变式问题：求2320162222[][][][]7777S =++++.解析：假设27k k a =，对任意的k a 不是整数，且满足32323132k k k k a a a ---++=.所以 323232313[][][]2122.k k k k k a a a ----++=--或 又因为322277k kk +-= ，所以322{}{}77k k+=，因此3{}{}k k a a += ，得32313123{}{}{}{}{}{}k k k a a a a a a --++=++=1， 所以3232313[][][]21k k k k a a a ---++=- ，所以672672672323231311282[][][](21)6727k k k k k k S a a a ---==⋅-=++=-=-∑∑.3、对应思想与高斯函数在解析几何中，方程对应了坐标平面内的一条曲线.取整符号[]1x =对应了数轴上的点[0,1)，高斯函数与解析几何相结合的问题中，往往体现了这种对应思想.例5、[]x 表示不超过x 的最大整数，则在平面直接坐标系xOy 中，满足[][]2013x y ⋅=的所有点(,)x y 组成的图形面积为 .解析：满足[],[]x a y b ==对应的(,)x y 所组成的图形就是不等式 1.1a x a b y b ≤<+≤<+ 围成的区域，其面积是1.因为2013367112013111833361==⨯=⨯=⨯=⨯，所以满足[][]2013x y ⋅=的点(,)x y 组成的图形面积为4416⨯=.点评：本题整数对([],[])x y 要联系到直角坐标系中的对应的区域，2013要想到所有的因式分解可能性.同样的思路请读者完成以下问题：设[]x 表示不超过实数x 的最大整数，则在平面上，由满足22[][]50x y +=的点所形成的图形面积是 .4、换元思想与高斯函数换元法是高中数学的重要思想，通过换元，把问题转化，使问题简化，怎样换元，如何换元,为什么这样换元，是一个非常值得探讨的问题.例6、对正整数,n 设n x 是关于x 的方程320nx x n +-=的实根，记[(1)]n n a n x =+（符号[]x 表示不超过x 的最大整数）.则23420111()1005a a a a ++++= .解析：设(1)t n x =+，则原方程转化为3320()(1)1n t t n n n +-=*++，设方程()*的解为n t ，容易验证(1)n n t n x =+，因此[][]n n a t =.设函数332()(1)1n f t t t n n n =+-++，则()f n =23(1)(1)n n n n -+++，(1)2f n +=.当2n ≥时，()0,(1)0f n f n <+>，所以(,1)n t n n ∈+，所以[](2)n a n n =≥. 所以23420111()1005a a a a ++++=12010(22011)10052⨯+=2013. 点评：本例利用换元思想，把原来要求整的表达式看成一个变量，这样只需要求换元后方程的解.利用零点定理寻找函数的解，只需要寻找两个正整数,1n n +，两个端点函数值异号，就得到该变量的取整后的值.本题很好地把换元思想，零点定理和高斯函数融合地结合. 例7、若[]x 表示不超过x 的最大整数，则关于x 的函数()|[]|f x x x a =-+存在最大值(),M a 则正实数a 的取值范围是 .解析：设,x a N α+=+，其中N 为整数，[0,1)α∈. 则 ()||||f x N a N a αα=+--=-，[0,1)α∈，则原问题只需求()||,[0,1)g a ααα=-∈能取到最大值时整数a 的取值范围. 通过作出函数图象，容易得到，当12a <，函数()g α 的最大值为(1)g ，但1取不到，因此不存在最大值；当1,2a ≥函数()g α最小值为(0),g 且0在定义域内.所以1.2a ≥点评：本题对取整表达式的进行换元，并不是常见的换元方法，而是结合了取整函数的特点的换元x a +换成一个整数加小数部分N α+，把得到了非常简单的表达式，使得原来表达式里既有取整符号又有绝对值符号的复杂的函数转化为一个常见的函数问题.本题体现了换元思想和取整符号合理结合. 5、单调思想与高斯函数,x y > 则[][]x y ≥.特别地，1,x y -≥ 则[][];x y >10x y >->，则[][]x y =或[][]1x y =+.这个性质表明取整函数是一个非减函数；还可以通过两个数的差的大小，估算两个数取整之后的差异.例8、设[]x 表示不超过x 的最大整数，2009[],k 1,2,,100k a k==，则这100个整数中不同的整数的个数为 .解析：以下事实：1,x y -≥ 则[][];x y > 若01x y <-<，则[][]x y =或[][]1x y =+.2009200920091(1)k k k k -=++,当[1,44]k ∈，20091;(1)k k >+ 当[45,99]k ∈，20091.(1)k k <+ 所以，12444544a a a a >>>>=;[45,100]k ∈,1k k a a +=或11k k a a +=-，且10020a =，由此得：4546100,,,a a a 中一共有44-20+1=25个数；1244,,,a a a 各不相同且4445a a >，所以一共有25+44=69个不同的整数.点评：本题通过比较相邻两个数的差的大小来判断取整之后的大小.从45项起，前后两项满足1k k a a +=或11k k a a +=-，且451004,20,a a == 得到45项到100项的不同个数为25个，显示了本题的精髓和巧妙之处，不禁让人醍醐灌顶！ 6、进制思想与高斯函数 例9、对正整数x ，记23[][][][],2222kx x x x m =++++其中k 为满足2kx ≥的最小整数，符号[]x 表示不超过x 的最大整数，x 与m 的差，即x m -称为正整数x 的“亏损数”.（如，100x =时，234567100100100100100100100[][][][][][][]972222222m =++++++=，3,x m -=因此，数100的“亏损数”为3.）则亏损数为9的最小正整数x 为 .解析：设正整数x 的2进制表示为1122102110[]222n n n n n n n x a a a a a a a a a a ----==⋅+⋅++⋅+， 0,01n k a a ≠=（或）则120112222n n n n a xa a a ---=⋅+⋅+++，得，1111112[]22[]2n n n n n n xa a a a a a ----=⋅+⋅+⋯+=则012210212212[][0]n n n n n n a a a a a a a a a a a a ----=-=1122[]n n x a a a --⋅⋅=2[]2xx -同理得到：12[]2[]2[][]2[]2222x x x x a =-=-，2231[]2[],[]2[]2222n n n x x x xa a +=-=-,所以012212[][][]2[][][][]2222222n n n n x x x x x x xa a a a x x +++++=-----=----因为122n n x +≤<，则k 取n 或1n +，当,k n =23[][][][]2222n x x x xm =++++，当1,k n =+ 231[][][][][]22222n n x x x x x m +=+++++=23[][][][]2222n x x x x++++，因此012n a a a a x m ++++=-，因此若x 亏损数是9，则代表x 的二进制表达式中的非零个数为9.因此，x 的最小值为872[111111111]2221511.=++++=点评：本题解题独特，构思巧妙，体现了进制与取整的内在联系.在不同的知识点之间可以相互联系，互相渗透，这也许是数学的奇妙之处吧！。

赏析与高斯函数有关的中考新定义问题1 高斯函数问题的提出早年，数学王子高斯在闲暇时发现并定义了取整函数，即设x ∈R ，用[x ]或int (x )[2]表示不超过x 的最大整数，并用"{}x "表示x 的非负纯小数,则[]y x =称为高斯函数，也叫取整函数。

高斯函数[x ]的定义域是R ,值域为Z ,其图象是不连续的水平线段。

在初中、高中数学竞赛中经常出现含有取整函数的问题。

笔者前些年在高三复习时发现高斯函数问题[1]在高考中频繁出现，同样的，高斯函数也已渗透到中考，多以阅读理解的新定义问题的形式出现在压轴题的位置。

创新意识的培养是现代数学教育的基本任务，应体现在数学教与学的过程之中。

学生自己发现和提出问题是创新的基础；独立思考、学会思考是创新的核心；归纳概括得到猜想和规律，并加以验证，是创新的重要方法。

创新意识的培养应该从义务教育阶段做起，贯穿数学教育的始终[8]。

陶行知指出：“创造力最能发挥的条件是民主。

”民主、平等、宽松、和谐、愉悦的教学气氛，能够使学生产生自觉参与的欲望，无顾忌地充分表达自己的创意和“心理安全”，为其创造性活动的开展提供必要的条件。

高斯函数[x ]有关的求值问题及方程问题，这类问题新颖有趣味性，备受命题者关注。

同时这类问题对初中生有较大难度。

下面本文从一些各地中考考题和一些数学竞赛题为例去体会高斯函数。

2 高斯函数有关的准备我们只提出本文需要的一些性质[]{}x x x =+，[]1x x x -<≤[]1x <+。

3 高斯函数有关问题的解决一．以高斯函数的定义为背景考察例1 （2016乐山16）高斯函数[x ]，也称为取整函数，即[x ]表示不超过x 的最大整数． 例如：[2.3]=2，[﹣1.5]=﹣2．则下列结论：①[﹣2.1]+[1]=﹣2；②[x ]+[﹣x ]=0；③若[x +1]=3，则x 的取值范围是2≤x ＜3； ④当﹣1≤x ＜1时，[x +1]+[﹣x +1]的值为0、1、2．其中正确的结论有 （写出所有正确结论的序号）．分析：①[﹣2.1]+[1]=﹣3+1=﹣2，正确；②错误，例如：[2.5]=2，[﹣2.5]=﹣3，2+（﹣3）≠0；③若[x +1]=3，则x 的取值范围是2≤ x ＜3，正确；④当﹣1≤ x ＜1时，0≤ x +1＜2，0＜﹣x +1≤2，∴[x +1]=0或1，[﹣x +1]=0或1或2，当[x +1]=1时，[﹣x +1]=2；当[﹣x +1]=1时，[﹣x +1]=1或0；所以[x +1]+[﹣x +1]的值为1、2，故错误．故答案为：①③．点评：根据“定义[x ]为不超过x 的最大整数”进行计算．【变式1】（2017崇仁）规定：用符号[x ]表示一个不大于实数x 的最大整数，例如：[3.69]=3，[3+1]=2，[﹣2.56]=﹣3，[﹣3]=﹣2．按这个规定，[﹣13﹣1]= ．分析：∵4133<<，∴3-13-4-<<，∴[]5-1-13-=．故答案为：﹣5．【变式2】（2015，永州）定义[x ]为不超过x 的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x ，下列式子中错误的是（ ）A ．[x ]=x （x 为整数）B ．0≤x ﹣[x ]＜1C ．[x +y ]≤[x ]+[y ]D ．[n +x ]=n +[x ]（n 为整数） 分析：A 、∵[x ]为不超过x 的最大整数，∴当x 是整数时，[x ]=x ，成立；B 、∵[x ]为不超过x 的最大整数，∴0≤x ﹣[x ]＜1，成立；C 、例如，[﹣5.4﹣3.2]=[﹣8.6]=﹣9，[﹣5.4]+[﹣3.2]=﹣6+（﹣4）=﹣10，∵﹣9＞﹣10，∴[﹣5.4﹣3.2]＞[﹣5.4]+[﹣3.2]，∴[x +y ]≤[x ]+[y ]不成立，D 、[n +x ]=n +[x ]（n 为整数），成立；故选：C ．美国著名心理学家布龙菲尔德说：“数学教学就是数学语言的教学”，可见数学不仅是一门科学，也是一种文化，更是一种语言---描述科学的语言。

最近有感于部分网友对高斯模糊滤镜的研究，现总结如下。

高斯模糊是数字图像模板处理法的一种。

其模板是根据二维正态分布（高斯分布）函数计算出来的。

正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到，C.F.高斯在研究测量误差时从另一个角度导出了它，P.S.拉普拉斯和高斯研究了它的性质。

一维正态分布的函数定义：在这个函数中，第一个参数μ是遵从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ,σ2)。

遵从正态分布的随机变量其概率规律为：取μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。

正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。

它的形状是中间高两边低，图像是一条位于x轴上方的钟形曲线。

当μ=0，σ2=1时，称为标准正态分布，记为N(0,1)。

两个参数的意义：μ－期望，σ2－方差。

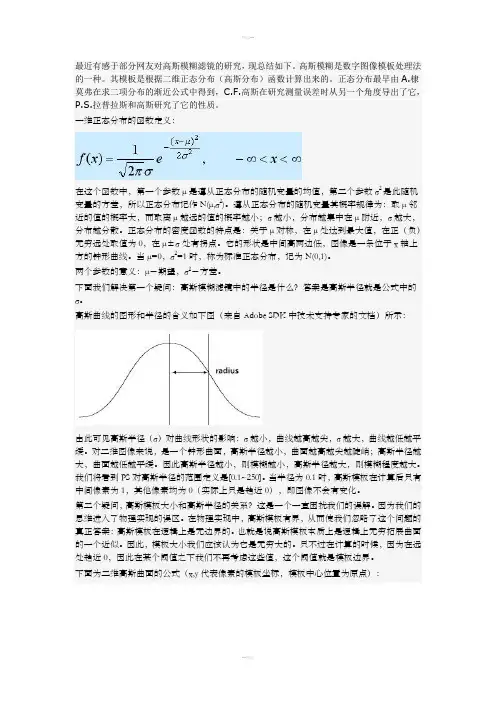
下面我们解决第一个疑问：高斯模糊滤镜中的半径是什么？答案是高斯半径就是公式中的σ。

高斯曲线的图形和半径的含义如下图（来自Adobe SDK中技术支持专家的文档）所示：由此可见高斯半径（σ）对曲线形状的影响：σ越小，曲线越高越尖，σ越大，曲线越低越平缓。

对二维图像来说，是一个钟形曲面，高斯半径越小，曲面越高越尖越陡峭；高斯半径越大，曲面越低越平缓。

因此高斯半径越小，则模糊越小，高斯半径越大，则模糊程度越大。

我们将看到PS对高斯半径的范围定义是[0.1~250]。

当半径为0.1时，高斯模板在计算后只有中间像素为1，其他像素均为0（实际上只是趋近0），即图像不会有变化。

第二个疑问，高斯模板大小和高斯半径的关系？这是一个一直困扰我们的误解。

因为我们的思维进入了物理实现的误区。

在物理实现中，高斯模板有界，从而使我们忽略了这个问题的真正答案：高斯模板在逻辑上是无边界的。

也就是说高斯模板本质上是逻辑上无穷拓展曲面的一个近似。

gis高斯函数GIS高斯函数GIS（地理信息系统）是一种用于收集、存储、管理、分析和展示地理数据的技术系统。

在GIS中，高斯函数是一种常用的空间分析方法，用于模拟地理现象的分布和插值。

本文将介绍GIS高斯函数的原理、应用和局限性。

一、高斯函数的原理高斯函数，又称为正态分布函数，是一种连续的数学函数，其曲线呈钟形，左右对称。

在GIS中，高斯函数被广泛应用于空间插值、地理统计和地理加权回归等领域。

高斯函数的数学表达式为：f(x) = (1 / (σ * √(2π))) * e^(-((x-μ)^2 / (2σ^2)))其中，f(x)表示函数的值，x为自变量，μ为均值，σ为标准差，e 为自然常数。

高斯函数的曲线在均值处达到峰值，随着离均值的距离增加，曲线逐渐减小。

二、高斯函数的应用1. 空间插值：GIS中常常需要通过已知点的属性值推算未知点的属性值。

高斯函数可以通过已知点的空间位置和属性值，对未知点进行插值计算。

通过高斯函数的插值结果，可以获得更加平滑和连续的空间分布。

2. 地理统计：高斯函数可以用于描述地理现象的分布特征。

例如，通过统计人口分布数据，可以使用高斯函数拟合出一个人口密度曲线，进而分析人口分布的集聚和离散情况。

3. 地理加权回归：在地理分析中，常常需要考虑空间自相关性。

高斯函数可以作为一种权重函数，用于对空间邻近性进行加权处理。

在地理回归分析中，使用高斯函数进行加权回归可以更准确地估计空间数据之间的关系。

三、高斯函数的局限性尽管高斯函数在GIS中有着广泛的应用，但也存在一些局限性。

首先，高斯函数的计算复杂度较高，特别是对于大规模数据集。

其次，高斯函数在边缘部分的衰减较慢，可能会导致插值结果过于平滑，忽略了局部的空间变化。

此外，高斯函数对异常值较为敏感，可能会导致插值结果受到极端值的影响。

四、总结GIS高斯函数是一种重要的空间分析工具，可以用于空间插值、地理统计和地理加权回归等应用中。

通过高斯函数的计算，可以获得更加平滑和连续的空间分布，并且考虑了空间自相关性。

浅析简单的高斯方程的解法广东省深圳市建文中学高中数学老师欧阳文丰一、知识概念介绍1、高斯函数的表示； [x]表示不超过x的整数部分,{x}表示x的小数部分。

2、高斯函数的基本性质；性质1： [x]≤x＜[x]+1 x-1＜[x] ≤x 0≤{x}<1性质2: [n+x]=n+[x],x为实数, n为整数性质3:{x+n}={x}, n为整数性质4:X= [x] + ｛χ｝3、简单的高斯方程；是指含有[x]表示不超过x的整数部分,{x}表示x的小数部分的简单方程。

求解简单的含高斯函数方程就是利用以上的性质进行转化来求解方程的未知数的值。

二、例题学习例1、解方程:[x]-4{x}=3,其中:[x]表示不超过x的整数部分,{x}表示x的小数部分。

解：把[x]-4{x}=3整理变形得：[x]= 4{x}+3因为0≤{x}<1，所以3≤4{x}+3＜7即3≤ [x] ＜7 [x] =3, 4, 5, 6。

(1)、当[x] =3时, 代入原方程得:3- 4{x}=3, 解得： {x}=0；所以x= [x] + {x}=3+0=3(2)、当[x] =4时, 代入原方程:4- 4{x}=3, 解得： {x}=；所以x= [x] + {x}=4+=(3)、当[x] =5,代入原方程: 5- 4{x}=3, 解得： {x}=； 所以x= [x] + {x}=5+=5. 5(4)、当[x] =6时,代入原方程得: 6- 4{x}=3, 解得：{x}=； 所以x= [x] + {x}=6+=综上所述， 方程[x]-4{x}=3 的解有四个， 分别为：x=3, , 5. 5, 。

例2、符号[X]表示不超过X 的最大整数.{X}表示X 的正的小数部分,求方程2[X]+5{X}+3=0的解 。

解： 由2[X]+5{X}+3=0得：{X}=(-3-2 [X]) ÷5因为0≤{x}<1 所以0≤ (-3-2 [X]) ÷5 ＜1解以上关于[X]的不等式得：≥ [X] ＞-4故[X]=-2, -3。

活跃在高考试卷中的高斯函数近年来，为创设新颖的问题情境，考查学生知识迁移能力，体现“以能力立意”，很多命题者把目光投向了高斯函数，并且由简单的直接利用定义到复杂的运用性质，难度越来越大.本文研究高斯函数的一些常用的性质，及其在高考试题中的简单运用.一、定义：设x R ∈，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，也叫取整函数.显然，任一实数都能写成整数部分与非负纯小数之和，即[]()01x x r r =+≤<. 二、常用性质：1、[]y x =的定义域是R ，值域是Z ，图像如图.2、对任意x R ∈，[][]11x x x x -<≤<+.证明：设[]()01x x r r =+≤<，于是[]01r x x ≤=-<, 所以[][]11x x x x -<≤<+. 3、若,n Z x R ∈∈，则[][]n x n x +=+.证明：设[]()1101x n x n r r +=++≤<，则[]1x x n n r =+-+, [][]1[][]x x n n r x n n =+-+=+-. 所以[][]n x n x +=+.4、若x R ∈，则[][][]1,,x x Z x x x Z ⎧--∉⎪-=⎨-∈⎪⎩证明：设[]()01x x r r =+≤<，则[]x x r -=--，[][]x x r ⎡⎤-=--⎣⎦ 若0r =，则[][][]x x x ⎡⎤-=-=-⎣⎦；若01r <<，则011r <-<，所以[][]1(1)x x r ⎡⎤-=--+-⎣⎦[][]11x x ⎡⎤=--=--⎣⎦.综上可得[][][]1,,x x Zx x x Z ⎧--∉⎪-=⎨-∈⎪⎩5、对任意,x y R ∈，[][][]x y x y +≥+.证明：设[]1x x r =+，[]2y y r =+，120,1r r ≤<，则[][]12x y x y r r +=+++，1202r r ≤+<. 若1201r r ≤+<，则[][][]x y x y +=+；若1212r r ≤+<，则12011r r ≤+-<, [][]121(1)x y x y r r +=++++-， 所以[][][]1x y x y +=++. 综上可得[][][]x y x y +≥+. 6、对任意,x y R ∈，[][][]x y x y -≤-.证明：由性质5知，[][][][]x y y x y y x -+≤-+=，所以[][][]x y x y -≤-. 7、对任意,x y R ∈，若x y ≤，则[][]x y ≤.证明：（反证法）若[][]x y >，则[][]0x y ->，所以整数[][]1x y -≥，即[][]1x y ≥+. 于是由性质2，[][]1x x y y ≥≥+>，这与已知x y ≤矛盾， 故[][]x y ≤. 8、对任意0,0x y ≥≥，[][][]xy x y ≥.证明：设0,0x y ≥≥且[]1x x r =+，[]2y y r =+, 120,1r r ≤<， 则[][][][]2112xy x y x r y r rr =+++. 因为0,0x y >>，120,1rr ≤<， 所以[][]21120x r y r rr ++≥，于是[][]xy x y ≥. 由性质7可知[][][][][]xy x y x y ⎡⎤≥=⎣⎦.特别地，对任意0,x n N +>∈都有[][]nx n x ≥.9、若1,0x y ≥≥， 则[][]y y x x ⎡⎤≤⎢⎥⎣⎦.证明：设1,0x y ≥≥，由性质8知[][]y y y x x x x ⎡⎤⎡⎤=⋅≥⋅⎢⎥⎢⎥⎣⎦⎣⎦. 又因为[]1x ≥，所以[][]y y x x ⎡⎤≤⎢⎥⎣⎦ 10、若,0n N x +∈≥，则[]x x n n ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦.证明：由性质2知[][]1x x x ≤<+. 又n N +∈，所以[][](1)n x nx n x ≤<+. 再由性质8知[][]n x nx ≤，由性质2知[]nx nx ≤，于是[][][](1)n x nx nx n x ≤≤<+,[][][]1nx x x n≤<+，所以[][]nx x n ⎡⎤=⎢⎥⎣⎦，x 用x n 代换，即得[]x x n n ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦.三、应用举例例1、2013年湖北文科8）x 为实数，[]x 表示不超过x 的最大整数，则函数()[]f x x x =-在R 上为A ．奇函数B ．偶函数C ．增函数D ． 周期函数 分析：由[]()01x x r r =+≤<知，[]()[0,1)f x r x x ==-∈，图像如图，可见，函数()[]f x x x =-是周期函数，选 D ．注：由图像可知，函数()[]f x x x =-是有界的、非奇非偶的、以1为周期的非单调函数，在每个区间[,1)n n +,（n Z ∈）上都是单调增函数.例2、（2013年陕西理科10）设[]x 表示不大于x 的最大整数，则对任意实数,x y ，有（ ）A.[][]x x -=-B.[][]22x x =C.[][][]x y x y +≤+D.[][][]x y x y -≤- 分析：由性质4、8、5知A. B. C.均不对，由性质6知D 是正确的.注：本题若根据[]x 的定义，取特殊值也可以淘汰掉A. B. C ．例3、（201２年四川理科16）记[]x 为不超过实数x 的最大整数. 例如，[2]2=，[1.5]1=，[0.3]1-=-.设a 为正整数，数列{}n x 满足1x a =，1[][]()2n nn ax x x n N *++=∈，现有下列命题：①当5a =时，数列{}n x 的前3项依次为5,3,2；②对数列{}n x 都存在正整数k ，当n k ≥时总有n k x x =； ③当1n ≥时，1n x ；④对某个正整数k ，若1k k x x +≥，则k x =．其中的真命题有____________．（写出所有真命题的编号）分析：对于①，5a =时，根据1[][]()2n nn ax x x n N *++=∈ 知15x =，251[]32x +==，3533[]22x +==.所以①为真.对于②，注意到3a =时，13x =,22x =,31x =,42x =,51x =,62x =,71x =，，此时数列{}n x 除第一项外，从第二项起以后的各项以2为周期重复出现，因此不存在正整数k ，当n k ≥时总有n k x x =.所以②为假.对于③，由条件知n x 是正整数，所以由性质3知[][]n n n n a ax x x x +=+.所以[][]22n n nna a x x x x ++=，[][][][]22n n nnaa x x x x ++=. 由性质10知[][][]22n n nna a x x x x ++=.又因为2n na x x +≥ 由性质8知[]2n n a x x +≥,从而1[][]12n nn a x x x ++=≥>（性质2），所以③为真. 对于④，因为n x 是整数，由性质3知1[][]()2n n n n n a x x x x x ++-=+-[][()]2n n n a x x x +=+-[][]2nn a x x -= [][]2n n ax x -=. 于是若1k k x x +≥，则0k ka x x -≥ ，又因为0k x >，所以2k x a ≤，k x ≤.又由③知k x ≥，所以k x ≤7知[]k x ⎡⎤=≤≤⎣⎦，从而[]k k x x ==.所以④为真. 综上可知，正确的编号为①③④注：本题难度较大，需要多次利用几个性质才能做出判断，特别是③④.例4、（2010年陕西理科10）某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于．．6．时再增选一名代表.那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数[]y x =（[]x 表示不大于x 的最大整数）可以表示为 ( )A. 10x y ⎡⎤=⎢⎥⎣⎦B. 310x y +⎡⎤=⎢⎥⎣⎦C. 410x y +⎡⎤=⎢⎥⎣⎦ D. 510x y +⎡⎤=⎢⎥⎣⎦分析：设)90(10≤≤+=ααm x . 当，时⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤≤10103103,60x m m x αα 1101103103,96+⎥⎦⎤⎢⎣⎡=+=⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤<x m m x αα时当，所以选B 注：本题也可以采用排除法：若56x =则5y =,排除C 、D ，若57x =则6y =，排除A ，所以选B例5、（2009年湖北文科9）设x R ∈,记不超过x 的最大整数为[]x ,令{}[]x x x =-，则12⎫⎪⎬⎪⎪⎩⎭，⎣⎦（ ） A. 是等差数列但不是等比数列 B. 是等比数列但不是等差数列 C. 既是等差数列又是等比数列 D. 既不是等差数列也不是等比数列分析：因为12<<，所以1=⎣⎦.又{}[]x x x =-故=-⎪⎪⎩⎭⎣⎦11122=-=. 而12，1，12成等比数列但不成等差数列，所以选B. 注：作为文科题，本题较简单，直接利用定义即可.例6、（2008年湖南理科10）设［x ］表示不超过x 的最大整数（如［2］=2, ［54］=1）,对于给定的n ∈N *,定义[][](1)(1)(1)(1)xn n n n x C x x x x --+=--+，x ∈[)1,+∞,则当x ∈3,32⎡⎫⎪⎢⎣⎭时，函数8x C 的值域是( )A.16,283⎡⎤⎢⎥⎣⎦B.16,563⎡⎫⎪⎢⎣⎭ C.284,3⎛⎫⋃ ⎪⎝⎭[)28,56 D.16284,,2833⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦分析：当3[,2)2x ∈时，[]1x =.8816(4,]3xC x =∈. 当[2,3)x ∈时，[]2x =，828756(1)x C x x x x⨯==-- 此时2211()[2,6)24x x x -=--∈，所以828(,28]3x C ∈. 于是81628(4,](,28]33x C ∈⋃，选D. 注：本题是对常见组合数计算公式的延拓，又结合取整函数，设计巧妙，构思新颖.由于x 未必是正整数，而根据定义在3,32⎡⎫⎪⎢⎣⎭内［x ］的值有两个，因此需要加以讨论, 再结合xn C 的定义研究8x C 的值域.。

与高斯函数有关的恒等式-概述说明以及解释1.引言1.1 概述概述高斯函数是一种在数学和物理领域广泛应用的特殊函数。

它由德国数学家高斯在18世纪末提出，并被广泛研究和应用于各个领域，如信号处理、图像处理、统计学以及自然科学等。

高斯函数不仅具有良好的数学性质，还具有许多重要的物理意义。

在本文中，我们将讨论高斯函数的定义及其一些基本性质，并介绍与高斯函数相关的一些重要恒等式。

这些恒等式是由高斯函数的特殊性质和运算规律导出的，对于解决实际问题和推导其他数学定理具有重要意义。

本文结构如下：第2部分将详细介绍高斯函数的定义与性质。

我们将从高斯函数的数学定义开始，并讨论它的图像、曲线特征以及一些重要的性质，如对称性、峰值和标准差等。

此外，我们还将介绍高斯函数在概率密度函数和误差函数中的应用。

第3部分将重点讨论与高斯函数相关的恒等式。

这些恒等式涉及到高斯函数的运算规律、积分性质以及与其他特殊函数的关系。

我们将详细介绍这些恒等式的推导过程，并给出一些实际应用的例子。

最后，结论部分将对本文内容进行总结，并展望未来对高斯函数及其相关恒等式的研究方向。

高斯函数作为一种重要的数学工具，在各个领域都有广泛的应用和深入的研究价值。

未来的研究可以着重于高斯函数在更复杂问题中的应用，以及与其他数学工具的结合，为解决实际问题提供更多的数学方法和技巧。

通过本文的阅读，读者将对高斯函数有更深入的了解，并了解到与高斯函数相关的一些重要恒等式的推导方法和应用。

希望本文能为读者提供有关高斯函数的全面信息，激发读者对高斯函数和相关数学工具的兴趣和研究热情。

文章结构部分的内容可以如下编写：1.2 文章结构本文主要分为三个部分：引言、正文和结论。

引言部分首先概述了与高斯函数有关的恒等式的重要性和应用背景。

然后介绍了本文的结构和目的，以给读者一个整体的了解。

正文部分主要包括两个小节。

第一小节（2.1 高斯函数的定义与性质）详细介绍了高斯函数的定义和一些基本性质，包括其数学表达式、图像特点以及常见的应用领域。

透彻理解高斯核函数背后的哲学思想与数学思想数据点转换到高维空间后，原始特征无关紧要。

仅仅计算测试数据与支持向量的点积，支持向量由SVM优化算法选择的特殊数据点。

在此，作一个类比如下：一个人看过湖泊，河流，溪流，浅滩等，但从未见过大海。

你怎么向这个人解释大海是什么？也许可以通过将海水中的水量与人们已经知道的水体中的水量相关联来解释。

简单与复杂的辩证：从线性模型到非线性模型简单性是一个古老朴素的哲学观念。

认识论和自然科学，对于世界的认识经历了由简单到复杂的过程。

复杂的事物与现象，背后存在简单的规律或过程；现实世界中，纯粹线性的模型是几乎不存在的，正如你在初中学习匀速运动一样，但在实际中，匀速运动的情况几乎很难找到，即使是定速，也会因外界的扰动而发生改变。

在机器学习实践中，也是如此，很多情况下需要非线性模型。

然而要构建复杂的非线性模型，往往是从简单的线性模型出发的。

线性模型很棒，因为它们易于理解且易于优化。

缺点是因为他们只能学习非常简单的决策边界。

神经网络可以学习更复杂的决策边界，但会丢失许多线性模型的漂亮凸性。

使线性模型表现为非线性的一种方法是转换输入。

例如，通过添加特征对作为附加输入。

在这样的表示上学习线性模型是凸的，但在除了非常低维空间之外的所有情况下都是计算上很难实现的。

你可能会问：不明确地扩展特征空间，是否可以在保留原始数据的同时，隐藏地处理特征扩张？令人惊讶的是，答案是肯定的，这就是核方法。

这是一个在当前空间下不可分的情况，我们的目标不是直接在当前维度寻找一个曲线来非线性划分类别，变换空间直接线性可分，这是哲学上简单性原则的应用：这个线性平面，返回到原来空间就是一个形状类似椭圆的决策边界。

这样就把问题解决了，从而找到了原空间的非线性分类边界。

这个原空间的复杂，实质上是由高维空间的简单演绎过来的。

通过核方法，可以很好的处理线性不可分问题。

简单性的哲学思想实质上就是，我们坚持寻找线性可分的转换问题，即变换数据，让它们线性可分，而变换数据的方法就是由低维到多维特征的一个特征空间变换。

例析与高斯函数有关问题的常考题型与备考建议刘海涛(安徽省芜湖市第一中学㊀２４１０００)摘㊀要:文章介绍了高斯函数的定义及其性质ꎬ例析高斯函数与其他知识的交汇问题的处理策略ꎬ最后给出复习备考的建议.关键词:高斯函数ꎻ高考备考ꎻ核心素养中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２３)０１－００２７－０５收稿日期:２０２２－１０－０５作者简介:刘海涛(１９８８－)ꎬ男ꎬ安徽省滁州人ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.１问题的提出«高考评价体系»指出:高考要从 知识立意 转向 能力立意 ꎬ考查学生的 关键能力 和 核心素养 .这就要求学生在学习中ꎬ学会灵活运用所学知识分析㊁解决问题ꎬ达到从 解题 向 解决问题 的转变.笔者在一轮复习的教学中ꎬ发现高斯函数频频出现在一些数学题中ꎬ学生面对此类问题常因方法不当ꎬ或运算过程繁杂ꎬ导致虽做对但耗时太多ꎬ或做错丢分ꎬ成绩不理想ꎬ而若能熟练掌握高斯函数的定义与性质ꎬ将其运用到解题中ꎬ定会事半功倍ꎬ提高解题正确率与效率.如何帮助学生在高考复习备考中ꎬ遇到与高斯函数有关的问题时ꎬ能够准确㊁快速㊁高效地解答呢?笔者通过梳理ꎬ现将该类问题整理成文ꎬ与读者交流ꎬ以期抛砖引玉.２高斯函数的介绍２.１高斯函数的定义设ｘɪＲꎬ用[ｘ]表示不超过ｘ的最大整数ꎬ则称ｙ＝[ｘ]为高斯函数ꎬ也叫取整函数.显然ꎬ其定义域为Ｒꎬ值域为Ｚ.高斯函数的定义域是连续的ꎬ但值域是离散的.我们把一个数的小数部分记作ｘ{}ꎬ则有ｘ＝[ｘ]＋ｘ{}ꎬ显然０ɤｘ{}<１.一般地ꎬ我们称ｙ＝ｘ{}为小数函数.２.２高斯函数的性质(１)若ｘɤｙꎬ则[ｘ]ɤ[ｙ]ꎻ(２)[ｎ＋ｘ]＝ｎ＋[ｘ]ꎬ其中ｎɪＺꎻ(３)ｘ－１<[ｘ]ɤｘ<[ｘ]＋１ꎻ(４)[ｘ]＋[ｙ]ɤ[ｘ＋ｙ]ꎻ(５)若ｘꎬｙȡ０ꎬ则[ｘｙ]ȡ[ｘ][ｙ]ꎻ(６)[－ｘ]＝－[ｘ]－１(ｘ不是整数)ꎬ－[ｘ](ｘ是整数)ꎻ{(７)若ｘ>０ꎬｎɪＮ∗ꎬ则在不超过ｘ的正整数中ꎬｎ的倍数共有[ｘｎ]个.３例析高斯函数与其他知识的交汇问题３.１利用高斯函数解函数问题３.１.１求函数解析式例１㊀某学校要召开学生代表大会ꎬ规定各班每１０人推选一名代表ꎬ当各班人数除以１０的余数大于６时再增选一名代表.那么ꎬ各班可推选代表人数ｙ与该班人数ｘ之间的函数关系用高斯函数ｙ＝[ｘ]可以表示为(㊀㊀).Ａ.ｙ＝[ｘ１０]㊀㊀㊀Ｂ.ｙ＝[ｘ＋３１０]Ｃ.ｙ＝[ｘ＋４１０]Ｄ.ｙ＝[ｘ＋５１０]解析㊀根据规定ꎬ当班级人数除以１０的余数分别为７ꎬ８ꎬ９时可增选一名代表ꎬ因此用取整函数可以表示为ｙ＝[ｘ＋３１０]ꎬ故选Ｂ.评注㊀该题主要考查学生的逻辑推理能力和综合运用数学知识的能力ꎬ另外该题可以用特殊值验证法.３.１.２求函数值例２㊀已知函数ｆ(ｘ)＝ｘ３ｌｎｘꎬ当ｆ(ｘ)的值域为(２ｅ６ꎬ＋¥)时ꎬ[ｌｏｇｘｆ(ｘ)]的值为.解析㊀求导得ｆᶄ(ｘ)＝ｘ２(３ｌｎｘ＋１).当０<ｘ<ｅ－１３时ꎬｆᶄ(ｘ)<０ꎬ当ｘ>ｅ－１３时ꎬｆᶄ(ｘ)>０ꎬ所以函数ｆ(ｘ)在(０ꎬｅ－１３)上单调递减且ｆ(ｘ)<０ꎬ在(ｅ－１３ꎬ＋¥)上单调递增.又因为ｆ(ｅ２)＝２ｅ６ꎬ所以ｘ>ｅ２.由ｌｏｇｘｆ(ｘ)＝ｌｏｇｘ(ｘ３ｌｎｘ)＝６＋２ｌｎ(ｌｎｘ)ｌｎｘꎬ设ｔ＝ｌｎｘꎬｈ(ｔ)＝６＋２ｌｎｔｔ(ｔ>２)ꎬ求导得ｈᶄ(ｔ)＝２(１－ｌｎｔ)ｔ２ꎬ当２<ｔ<ｅ时ｈᶄ(ｔ)>０ꎬ当ｔ>ｅ时ｈᶄ(ｔ)<０ꎬ所以函数ｈ(ｔ)在(２ꎬｅ)上单调递增ꎬ在(ｅꎬ＋¥)上单调递减.则６<ｈ(ｔ)ɤｈ(ｅ)＝６＋２ｅ.即６<ｌｏｇｘｆ(ｘ)ɤ６＋２ｅ.所以[ｌｏｇｘｆ(ｘ)]＝６.评注㊀该题的难度较大ꎬ主要考查利用导数研究函数的单调性与值域ꎬ换元法求复合函数值域等ꎬ体现了逻辑推理㊁直观想象㊁数学运算等数学核心素养.３.１.３求函数的值域(或最值)例３㊀对于给定的ｎɪＮ∗ꎬ定义Ｃｘｎ＝ｎ(ｎ－１) (ｎ－[ｘ]＋１)ｘ(ｘ－１) (ｘ－[ｘ]＋１)(ｘȡ１)ꎬ则当ｘɪ[３２ꎬ３)时ꎬ函数Ｃｘ８的值域是.解析㊀当ｘɪ[３２ꎬ２)时ꎬ[ｘ]＝１ꎬＣｘ８＝８ｘ单调递减ꎬ则Ｃｘ８ɪ(４ꎬ１６３]ꎻ当ｘɪ[２ꎬ３)时ꎬ[ｘ]＝２ꎬ所以Ｃｘ８＝５６ｘ(ｘ－１)单调递减ꎬ则Ｃｘ８ɪ(２８３ꎬ２８].综上ꎬ函数Ｃｘ８的值域为(４ꎬ１６３]ɣ(２８３ꎬ２８].评注㊀该题属于新定义题ꎬ解答的关键在于对定义的理解及变量的分段讨论ꎬ这也体现了高斯函数是一种分段函数的属性ꎬ考查了学生逻辑推理㊁数学运算的核心素养.例４㊀定义在Ｒ上的函数ｆ(ｘ)＝[２ｘ]＋[４ｘ]＋[８ｘ]ꎬ若Ａ＝ｙ｜ｙ＝ｆ(ｘ)ꎬ０ɤｘ<１{}ꎬ则Ａ中元素的最大值和最小值之和为.解析㊀记Ｍｎ＝[ｎ８ꎬｎ＋１８)(ｎɪＮ且ｎɤ７)ꎬ则ɣ７ｎ＝０Ｍｎ＝[０ꎬ１).当ｘɪＭｎ时ꎬｆ(ｘ)＝[２ｘ]＋[４ｘ]＋[８ｘ]＝[ｎ４]＋[ｎ２]＋[ｎ]ꎬＡ中元素的最大值和最小值分别为函数ｆ(ｘ)的最大值和最小值ꎬ易知ｎ＝０时ｆ(ｘ)取最小值０ꎬｎ＝７时ｆ(ｘ)取最大值１１.故最大值和最小值之和为１１.评注㊀集合Ａ为函数ｙ＝ｆ(ｘ)(０ɤｘ<１)的值域ꎬ由此问题转化为求函数的最大值与最小值的和ꎬ求该函数最值的关键在于ꎬ根据高斯函数的定义恰当地分段讨论ꎬ该题很好地考查了分类讨论思想.３.１.４判断函数的性质例５㊀已知函数ｆ(ｘ)＝ｓｉｎ[ｃｏｓｘ]＋ｃｏｓ[ｓｉｎｘ]ꎬ关于ｆ(ｘ)有下列四个结论:①ｆ(ｘ)的一个周期为２πꎻ②ｆ(ｘ)是非奇非偶函数ꎻ③ｆ(ｘ)在(０ꎬπ)上单调递减ꎻ④ｆ(ｘ)的最大值为２.其中所有结论正确的编号是(㊀㊀).Ａ.①②④㊀Ｂ.②④㊀Ｃ.①③㊀Ｄ.①②解析㊀由ｆ(ｘ＋２π)＝ｓｉｎ[ｃｏｓ(ｘ＋２π)]＋ｃｏｓ[ｓｉｎ(ｘ＋２π)]＝ｓｉｎ[ｃｏｓｘ]＋ｃｏｓ[ｓｉｎｘ]＝ｆ(ｘ)ꎬ得ｆ(ｘ)的一个周期为２πꎬ则编号①正确ꎻ由ｆ(－ｘ)＝ｓｉｎ[ｃｏｓ(－ｘ)]＋ｃｏｓ[ｓｉｎ(－ｘ)]＝ｓｉｎ[ｃｏｓｘ]＋ｃｏｓ[－ｓｉｎｘ]ꎬ知ｆ(－ｘ)＋ｆ(ｘ)＝０与ｆ(－ｘ)＝ｆ(ｘ)两式均不恒成立ꎬ则编号②正确ꎻ当ｘɪ(０ꎬπ２)时ꎬ有０<ｃｏｓｘ<１且０<ｓｉｎｘ<１ꎬ所以ｆ(ｘ)＝ｓｉｎ０＋ｃｏｓ０＝１为定值ꎬ则编号③错误ꎻ由ｆ(０)＝ｓｉｎ[ｃｏｓ０]＋ｃｏｓ[ｓｉｎ０]＝ｓｉｎ１＋ｃｏｓ０>ｓｉｎπ４＋１>２ꎬ知编号④错误.评注㊀该题是一道高斯函数与三角函数结合的判断函数性质的问题ꎬ考查了学生的数学运算㊁逻辑推理等数学核心素养.３.１.５函数的零点问题例６㊀已知函数ｆ(ｘ)＝２ｘｘ{}－ｘ－１ꎬ则函数的的所有零点之和为(㊀㊀).Ａ.－１㊀Ｂ.０㊀㊀Ｃ.１㊀㊀Ｄ.２解析㊀由ｆ(０)ʂ０ꎬ知函数ｆ(ｘ)的零点即为方程２ｘ{}＝１＋１ｘ的根ꎬ作出函数ｙ＝２ｘ{}与ｙ＝１＋１ｘ的图象ꎬ两函数图象的交点除点(－１ꎬ０)外ꎬ其余交点均关于点(０ꎬ１)中心对称ꎬ则函数ｆ(ｘ)的所有零点和为－１ꎬ故选Ａ.评注㊀该题是一道与小数函数有关的函数零点问题ꎬ蕴含了函数与方程㊁数形结合等数学思想ꎬ考查的知识点较多ꎬ难度较大ꎬ尤其是对于函数ｙ＝２ｘ{}与ｙ＝１＋１ｘ的图象交点ꎬ除点(－１ꎬ０)外其余点关于点(０ꎬ１)对称这一性质的发现.３.２高斯函数与方程交汇问题例７㊀设ｘɪＲꎬ关于ｘ的方程[３ｘ＋１]＝２ｘ－１２的全部实根之和为.解法１㊀设２ｘ－１２＝ｋ(ｋɪＺ)ꎬ则ｘ＝２ｋ＋１４.有３ｘ＋１＝ｋ＋１＋２ｋ＋３４.所以原方程等价于[２ｋ＋３４]＝－１.即－１ɤ２ｋ＋３４<０.即－７２ɤｋ<－３２.则ｋ＝－３或－２ꎬ相应的ｘ＝－５４或－３４ꎬ于是全部实根之和为－２.解法２㊀由３ｘ<[３ｘ＋１]ɤ３ｘ＋１ꎬ得３ｘ<２ｘ－１２ɤ３ｘ＋１.解得－３２ɤｘ<－１２.则－７２ɤ３ｘ＋１<－１２ꎬ[３ｘ＋１]＝－１ꎬ－２ꎬ－３ꎬ－４.当２ｘ－１２＝－１时ꎬｘ＝－１４(舍)ꎻ当２ｘ－１２＝－２时ꎬｘ＝－３４ꎻ当２ｘ－１２＝－３时ꎬｘ＝－５４ꎻ当２ｘ－１２＝－４时ꎬｘ＝－７４(舍).综上ꎬ方程全部实根和为－２.评注㊀解答该题的关键在于对高斯函数定义和性质的理解ꎬ是一道较简单的方程题ꎬ考查了学生的逻辑推理㊁数学运算核心素养.３.３高斯函数与不等式交汇问题例８㊀已知ｘ>０ꎬ不等式[ｘ]ｘ{}<ｘ－１的解集为.解析㊀由ｘ＝[ｘ]＋ｘ{}ꎬ不等式[ｘ]ｘ{}<ｘ－１变形为([ｘ]－１)(ｘ－[ｘ]－１)<０ꎬ有ｘ<[ｘ]＋１恒成立.所以不等式等价于[ｘ]－１>０.即[ｘ]>１ꎬ即ｘȡ２.所以不等式解集为[２ꎬ＋¥).评注㊀解答该题的关键在于对不等式的合理变形ꎬ及高斯函数性质ｘ<[ｘ]＋１的运用ꎬ考查了逻辑推理㊁数学运算的数学核心素养.３.４高斯函数与数列交汇问题３.４.１数列通项问题例９㊀已知函数ｆ(ｘ)＝[ｘ[ｘ]]ꎬ当ｘɪ[０ꎬｎ)(ｎɪＮ∗)时ꎬ设函数ｆ(ｘ)的值域为Ａꎬ记集合Ａ中的元素个数为ａｎꎬ则式子ａｎ＋９０ｎ的最小值为.解析㊀当ｘɪ[０ꎬ１)时ꎬｆ(ｘ)＝[ｘ[ｘ]]＝０ꎻ当ｘɪ[ｋꎬｋ＋１)(ｋɪＮ∗且ｋɤｎ－１)时ꎬｘ[ｘ]＝ｋｘɪ[ｋ２ꎬｋ２＋ｋ)ꎬ则ｆ(ｘ)＝ｋ２ꎬｋ２＋１ꎬ ꎬｋ２＋ｋ－１ꎬ共有ｋ个取值.所以ａｎ＝１＋１＋２＋ ＋(ｎ－１)＝１２ｎ(ｎ－１)＋１.则ａｎ＋９０ｎ＝１２(ｎ＋１８２ｎ)－１２.易知当ｎ＝１３或１４时取得最小值为１３.评注㊀解答该题的关键在于抓住高斯函数的定义ꎬ将区间进行分段讨论.３.４.２数列求和问题例１０㊀数列ａｎ{}满足ａ１＝３ꎬａｎ＋１－ａｎ＝２ｎ＋２ꎬ则数列[ａｎ]的前２０２２项和为.解析㊀当ｎȡ２时ꎬａｎ＝(ａｎ－ａｎ－１)＋(ａｎ－１－ａｎ－２)＋ ＋(ａ２－ａ１)＋ａ１＝２ｎ＋２(ｎ－１)＋ ＋４＋３＝ｎ２＋ｎ＋１.又ａ１＝３满足ａｎ＝ｎ２＋ｎ＋１ꎬ所以ａｎ＝ｎ２＋ｎ＋１.由ｎ２<ｎ２＋ｎ＋１<(ｎ＋１)２ꎬ得[ａｎ]＝ｎ.则数列[ａｎ]的前２０２２项和为１＋２＋ ＋２０２２＝２０２３ˑ１０１１.评注㊀累加法求出数列通项后ꎬ根据ｎ２<ａｎ<(ｎ＋１)２ꎬ结合高斯函数定义得到[ａｎ]＝ｎꎬ从而解决问题.３.５高斯函数与平面几何交汇问题例１１㊀已知点集Ｐ＝{(ｘꎬｙ)｜[ｘ]２＋[ｙ]２＝１}ꎬ则点集Ｐ表示的平面区域的面积是.解析㊀[ｘ]２＋[ｙ]２＝１等价于[ｘ]＝０ꎬ[ｙ]＝－１{或[ｘ]＝０ꎬ[ｙ]＝１{或[ｘ]＝－１ꎬ[ｙ]＝０{或[ｘ]＝１ꎬ[ｙ]＝０.{即０ɤｘ<１ꎬ－１ɤｙ<０{或０ɤｘ<１ꎬ１ɤｙ<２{或－１ɤｘ<０ꎬ０ɤｙ<１{或１ɤｘ<２ꎬ０ɤｙ<１.{易知相应的平面区域为四个边长为１的正方形ꎬ故面积和为４.评注㊀根据高斯函数的定义ꎬ逐一表示出平面区域对应的不等式组ꎬ便可发现平面区域为４个正方形.３.６高斯函数与二项式定理交汇问题例１２㊀已知ｃｎ＝[(２＋１)ｎ](ｎɪＮ∗)ꎬ则ｃ２０２２除以４的余数为.解析㊀由题意ꎬ设ａ＝(２＋１)２０２２ꎬｂ＝(２－１)２０２２.显然０<ｂ<１ꎬ则ａ＋ｂ＝２[１＋Ｃ２２０２２(２)２＋Ｃ４２０２２(２)４＋ ＋Ｃ２０２２２０２２(２)２０２２].显然Ｃ２２０２２(２)２＋Ｃ４２０２２(２)４＋ ＋Ｃ２０２２２０２２(２)２０２２为偶数ꎬ记作２ｋ(ｋɪＮ∗).则ａ＋ｂ＝２(２ｋ＋１)＝４ｋ＋２.所以ｃ２０２２＝[ａ]＝[４ｋ＋２－ｂ]＝４ｋ＋１＋[１－ｂ]＝４ｋ＋１.故ｃ２０２２除以４的余数为１.评注㊀解答该题的关键在于理解二项式定理展开式的结构和高斯函数的定义ꎬ通过构造对偶式法找出(２＋１)２０２２的整数部分值ꎬ该题属于难题.４有关高考复习备考的两点建议«普通高中数学课程标准(２０１７年版)»指出:在数学高考命题中ꎬ考查内容应围绕数学内容主线ꎬ聚焦学生对重要数学概念㊁性质㊁方法的理解和应用ꎬ强调基础性ꎬ注重数学本质和通性通法.在高考备考教学中ꎬ教师应加强基础知识㊁基本技能和基本数学思想方法的训练ꎬ以达到提高学生数学关键能力和数学核心素养的目的.基于此ꎬ笔者提出以下高考备考建议.４.１夯实基本知识ꎬ以不变应万变通过文中对与高斯函数有关问题的整理发现ꎬ该类问题主要考查高斯函数的概念与基本性质ꎬ考查的形式主要以选择㊁填空为主ꎬ难度也以中等㊁容易题为主.因此ꎬ我们在复习备考的过程中ꎬ要通过对该类试题的研究ꎬ归纳总结出高考考查的典型题型及其解题方法ꎬ构建完整的知识脉络和方法体系ꎬ熟练掌握与高斯函数有关的典型问题的通性通法ꎬ形成解题模型.只有扎实掌握了这些通性通法ꎬ才能在高考中游刃有余地处理该类问题.４.２渗透思想方法ꎬ提高核心素养数学思想是对数学知识的本质认识ꎬ是数学的精髓ꎬ是数学基础知识和数学能力之间的一座 桥梁 .通过上文的梳理ꎬ我们发现与高斯函数有关的问题主要考查分类讨论㊁数形结合㊁转化与化归等数学思想方法ꎬ如文中的例４考查了分类讨论的思想ꎬ例６将函数的零点个数转化为两个函数图象的交点个数ꎬ考查了转化与化归㊁数形结合的数学思想.笔者认为复习备考的教学中注重数学思想的渗透ꎬ可以帮助学生优化认知结构ꎬ学会用数学的眼光观察世界ꎬ用数学的思维思考世界ꎬ用数学的语言表达世界.数学学科核心素养的内涵包括数学核心知识㊁核心能力㊁核心品质ꎬ主要由数学抽象㊁逻辑推理㊁数学建模㊁直观想象㊁数学运算㊁数据分析等六个方面组成ꎬ这些数学核心素养既有独立性ꎬ又相互交融ꎬ形成一个有机整体.数学核心素养不是具体的知识和技能ꎬ也不是一般意义上的数学能力ꎬ它基于数学知识技能ꎬ但高于具体的数学知识技能.因此ꎬ笔者认为在高考复习备考中ꎬ我们广大一线教师不仅要重视解题方法的指导ꎬ更要重视对学生核心素养的提高ꎬ 授之以鱼不如授之以渔 ꎬ学生的数学素养提高了ꎬ解题能力和解题效率自然提高ꎬ无论高考题型如何变化ꎬ也定能在高考中 以不变应万变 ꎬ顺利取得高考的胜利.参考文献:[１]教育部考试中心.中国高考评价体系[Ｍ].北京:人民教育出版社ꎬ２０１９.[２]刘海涛.例析构造对偶式在解题中的应用[Ｊ].数理化学习(高中版)ꎬ２０２１(０４):１４－１７. [３]中华人民共和国教育部.普通高中数学课程标准(２０１７年版)[Ｍ].北京:人民教育出版社ꎬ２０１８.㊀[４]刘海涛.设计逻辑连贯的问题链追求自然流畅的数学教学 以 数系的扩充和复数的概念 教学为例[Ｊ].课程教材教学研究(中教研究)ꎬ２０２１(Ｚ２):７９－８３.[５]刘海涛.基于核心素养的 问题链 课堂教学实践研究 以 基本不等式 第一课时教学为例[Ｊ].中小学教学研究ꎬ２０２１ꎬ２２(０３):２１－２７.[责任编辑:李㊀璟]。

文理导航2010/8WEN LI DAO HANG高考中高斯函数相关问题探幽文/陆鹏随着新课程改革的不断推进和完善，高考命题越来越把学生的能力的考查放在第一位，高考命题的取材也随即变得越来越广阔，以往属于竞赛热点的内容常作为高考的命题素材，高斯取整函数就是其中之一，“高斯函数”是初等代数中的一个重要概念，但是由于高斯函数既能考查学生的知识迁移能力，又能考查学生的思维严谨性、周密性和条理性，符合新课程的理念。

近年来一直受到命题者的青睐，本文通过实例来研究高斯函数的高考命题动向。

一、概念定义函数y=[x]，其中[x]是不超过x 的最大整数，x ∈R 为高斯函数，又称取整函数.在实数轴R （箭头向右）上，[x]是在点x 左侧的第一个整数点，当x 是整数时[x]就是x 。

由[x]的定义不难得到如下常用的性质：（1）y=[x]的定义域为R ，值域为Z ；（2）对任意实数x ，都有x=[x]+{x},且0≤{x}＜1.（3）y=[x]是不减函数，即若x 1≤x 2则[x 1]≤[x 2]，其图像如图所示。

二、试题赏析1．高斯函数与数列例1（2006年北京西城抽样试题）对于一切实数x,令[x]为不大于x 的最大整数,则f(x)=[x]称为高斯函数或取整函数。

计算f(-0.3)+f(1)+f(1.3)=;若解析解此题需要注意两点（1）x ∈R （2）准确理解[x]的意义。

[x]是整数，是小于或等于x 的最大整数。

把握住这两点第一小题不难解决，答案为-1+1+1=1。

第二小题由知，，，，，……规律很清楚，可以求得。

我们还可以进一步研究S 3n ：例2．已知取整函数y=[x]，求[log 21]+[log 22]+[log 23]+[log 24]+∧＋[log 21024]的值。

解析结合对数知识可得，原式==，设，则，于是所以，原式=。

可以再考虑一般情形，即求其中，解题时可设，读者可以一试。

赏析高斯函数的引入，使得试题新颖别致，让人有耳目一新的感觉。

高斯分布函数解析高斯模糊是一种图像模糊滤波器，它用正态分布计算图像中每个像素的变换。

N 维空间正态分布方程为在二维空间定义为其中r是模糊半径 (r2 = u2 + v2)，σ 是正态分布的标准偏差。

在二维空间中，这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆。

分布不为零的像素组成的卷积矩阵与原始图像做变换。

每个像素的值都是周围相邻像素值的加权平均。

原始像素的值有最大的高斯分布值，所以有最大的权重，相邻像素随着距离原始像素越来越远，其权重也越来越小。

这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果，参见尺度空间实现。

理论上来讲，图像中每点的分布都不为零，这也就是说每个像素的计算都需要包含整幅图像。

在实际应用中，在计算高斯函数的离散近似时，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。

通常，图像处理程序只需要计算(6σ + 1) * (6σ + 1)的矩阵就可以保证相关像素影响。

除了圆形对称之外，高斯模糊也可以在二维图像上对两个独立的一维空间分别进行计算，这叫作线性可分。

这也就是说，使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。

从计算的角度来看，这是一项有用的特性，因为这样只需要 O(n * M * N) + O(m * M * N)计算，而不可分的矩阵则需要O(m * n * M * N)次计算，其中M,N是需要进行滤波的图像的维数，m、n是滤波器的维数。

对一幅图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果，大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。

例如，使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于一次半径为 10 的高斯模糊效果，sqrt(6 * 6 + 8 * 8) = 10。

根据这个关系，使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。

数学奥赛辅导 第五讲 高斯函数知识、方法、技能这一讲介绍重要的数论函数][x y =，称为高斯函数，又称取整函数. 它是数学竞赛热点之一.定义一：对任意实数][,x x 是不超过x 的最大整数，称][x 为x 的整数部分.与它相伴随的是小数部分函数].[}{},{x x x x y -==由][x 、}{x 的定义不难得到如下性质：（1）][x y =的定义域为R ，值域为Z ；}{x y =的定义域为R ，值域为)1,0[ （2）对任意实数x ，都有1}{0},{][<≤+=x x x x 且. （3）对任意实数x ，都有x x x x x x ≤<-+<≤][1,1][][.（4）][x y =是不减函数，即若21x x ≤则][][21x x ≤，其图像如图I －4－5－1；}{x y =是以1为周期的周期函数，如图I －4－5－2.图Ⅰ—4—5—1 图Ⅰ—4—5—2（5）}{}{];[][x n x x n n x =++=+.其中*∈∈N n R x ,. （6）∑∑==∈≥+≥++≥+ni iin i iR xx x y x y x x y x y x 11],[][};{}{}{{];[][][；特别地，].[][ba nb na ≥（7）][][][y x xy ⋅≥，其中+∈R y x ,；一般有∑∏=+=∈≥ni iin i iR xx x 11],[][；特别地，*∈+∈≤N n R x x x n n ,],[][.（8）]][[][nx n x =，其中*∈+∈N n R x ,. 【证明】（1）—（7）略.（8）令Z m m nx ∈=,][，则1+≤≤m nxm ，因此，)1(+<≤m n x nm .由于nm ， N m n ∈+)1(，则由（3）知，),1(][+<≤m n x nm 于是，.]][[,1][m nx m n x m =+<≤故 证毕.取整函数或高斯函数在初等数论中的应用是基于下面两个结论.定理一：*∈+∈N n R x ,，且1至x 之间的整数中，有][nx 个是n 的倍数.【证明】因n n xx n n x n x n x nx ⋅+<≤⋅+<≤)1]([][,1][][即，此式说明：不大于x 而是n 的倍数的正整数只有这nx ][个：.][,,2,n nxn n ⋅定理二：在n ！中，质数p 的最高方次数是.][][][)!(32 +++=pnp n p n n p【证明】由于p 是质数，因此!n 含p 的方次数)!(n p 一定是1，2，…，n n ,1-各数中所含p 的方次数的总和.由定理一知，1，2，…，n 中有][p n 个p 的倍数，有][2pn个p 2的倍数，…，所以.][][)!(2 ++=pnp nn p 此定理说明：M p n n p ⋅=)!(!，其中M 不含p 的因数.例如，由于]72000[]72000[)!2000(72+= +…=285+40+5=330，则2000！=7330·M ，其中7 M .定理三：（厄米特恒等式）][]1[]2[]1[][,,nx nn x n x n x x N n R x =-+++++++∈∈ 则 【证法1】引入辅助函数].1[]2[]2[]1[][][)(n n x n n x n x n x x nx x f -+--+--+-+--= 因=+)1(nx f …)(x f =对一切R x ∈成立，所以)(x f 是一个以n 1为周期的周期函数，而当]1,0[nx ∈时，直接计算知0)(=x f ，故任意R x ∈，厄米特恒等式成立.【证法2】等式等价于}].{[][]1}[{]1}[{}][{][x n x n nn x n x x x n +=-++++++ 消去][x n 后得到与原等式一样的等式，只不过是对)1,0[∈x ，则一定存在一个k 使得n k x n k <≤-1，即k nx k <≤-)1(，故原式右端.1][-==k nx 另一方面，由nkx n k <≤-1知，n n k x n n k n i k x n i k n k n x n k n k n x n k 12,,1,,221,11-+<≤-+++<≤++<+≤++<+≤ ，在这批不等式的右端总有一个等于1，设k n t n t k -==+即,1. 这时，==+= ]1[][nx x 0][=-+n k n x ，而1]1[]1[=-+==+-+n n x n k n x ，因此原式的左端是1-k 个1之和，即左端.1-=k 故左=右.【评述】证法2的方法既适用于证明等式，也适用于证明不等式.，这个方法是：第一步“弃整”，把对任意实数的问题转化为)1,0[的问题；第二步对)1,0[分段讨论.高斯函数在格点（又叫整点）问题研究中有重要应用. 下面给出一个定理. 定理四：设函数],[)(b a x f y 在=上连续而且非负，那么和式∑≤<bt a b a t t f ],[)](([为内的整数）表示平面区域)(0,x f y b x a ≤<≤<内的格点个数.特别地，有（1）位于三角形：d x c b ax y ≤<>+=,0内的格点个数等于∑≤<+dx c x b ax 且]([为整数）；（2）1),(=q p ，矩形域]2,0;2,0[pq 内的格点数等于.2121][][2/02/0∑∑<<<<-⋅-=+q x p y q p y pq x q p （3）0>r ，圆域222r y x ≤+内的格点个数等于∑≤<--++2/0222]2[4][8][41r x r x r r .（4）0>n ，区域：n xy y x ≤>>,0,0内的格点个数等于∑<<-nx n x n 02][][2. 这些结论通过画图即可得到.赛题精讲例1：求证：,2!211--=⇔k n n n 其中k 为某一自然数. （1985年第17届加拿大数学竞赛试题） [证明]2为质数，n!中含2的方次数为∑∞==1].2[)!(2t tn n 若∑∑∞=-=--------=-=++++====1111221111122221]2[]2[)!(2,2t k t k k t k t k k n n n 则故!.|21n n -反之，若n 不等于2的某个非负整数次幕，可设n=2sp ，其中p >1为奇数，这时总可以找出整数t ，使+++=<<--+ ]2[]2[)!(22!,222211p p n n p s s t s t 的方次数为中所含于是 ≤++- 0]2[p t s ].2[]22[])12(2[])222[(21p n p p p p t s t s s t t s t s s s -------+=-=-=+++由于12,2)!(22!,2]2[,221----≤-=-<<n t s t s n n n p 则的方次数中含故则n !.这与已知矛盾，故必要性得证.例2：对任意的∑∞=+*+=∈01].22[,K k kn S N n 计算和 （第10届IMO 试题）【解】因]212[]22[11+=+++k k n n 对一切k =0,1,…成立，因此，].2[]22[]212[111+++-⋅=+k k k nn n 又因为n 为固定数，当k 适当大时,.)]2[]2([,0]2[,1201n nn S n n K k k k k ==-==<∑∞=+ 故从而例3：计算和式.]503305[502的值∑==n n S （1986年东北三省数学竞赛试题） 【解】显然有：若.,,1][][][,1}{}{R y x y x y x y x ∈++=+=+则503是一个质数，因此，对n=1,2,…,502, 503305n 都不会是整数，但503305n +,305503)503(305=-n可见此式左端的两数的小数部分之和等于1，于是，[503305n ]+.304]503)503(305[=-n 故 ∑∑===⨯=-+==25115021.76304251304]),503)503(305[]503305([]503305[n n n n n S例4：设M 为一正整数，问方程222}{][x x x =-，在[1，M]中有多少个解？ （1982年瑞典数学竞赛试题）【解】显然x =M 是一个解,下面考察在[1，M]中有少个解.设x 是方程的解.将222}{}{}{2][x x x x x +⋅+=代入原方程，化简得=}]{[2x x,1}{0].}{}]{[2[2<≤+x x x x 由于所以上式成立的充要条件是2[x ]{x }为一个整数. .1)1(],1[,.)1())1(21(2),1[,11.2)1,[),12,,1,0(2}{,][个解中有原方程在因此个解中方程有可知在又由于个解中方程有即在则必有设+--⋅=-+++-≤≤+-==∈=M M M M M M M M m m m m m k mkx N m x例5：求方程.051][4042的实数解=+-x x （第36届美国数学竞赛题） 【解】.0][,1][][不是解又因<+<≤x x x x⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥>⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥<⎩⎨⎧≤-->--⎪⎩⎪⎨⎧≤+->+-+∴.217][,23][,211][;217][,23][,25][.07][2)(3][2(.0)11][2)(5][2(.051][4][4,051][40)1]([422x x x x x x x x x x x x x x 或.2269,02694;2229,02294;2189,01894;229,0294:,876][2][2222==-==-==-==-==x x x x x x x x x x 分别代入方程得或或或解得经检验知，这四个值都是原方程的解. 例6：.][3]3[2]2[1][][:,,nnx x x x nx N n R x ++++≥∈+∈*证明 （第10届美国数学竞赛试题）这道题的原解答要极为复杂，现用数学归纳法证明如下. 【证明】.,2,1,][2]2[][ =+++=k kkx x x A k 令 由于.,1],[1命题成立时则==n x A.,,,],[][][][][][][])[])1([(]))2[(]2([])1[(]([][]2[])2[(])1[(][])1[(]2[][][])1[(]2[][][])1[(]2[][)(:].[],2[22,],)1[()1()1(],[,][,][,].)1[(,],2[],[,1122112111221111121证毕均成立故原不等式对一切命题成立时即故相加得所以成立对一切即因为即有时命题成立设*---------∈=≤∴=+++≤++-++-++-+=+++-+-++-+++≤++++++-+++=+-+++=+++-==--=---=-=-=--≤≤≤-≤N n k n kx A kx k kx kx kx kx kx x x k x k x x k x x x x k x k kx x k x x A A A A kx x k x x kA kx x k x x A A A kA x A x A A x k A k A k kx kA kA k kx kA kA kkx A A x k A x A x A k n k k k k k k k k k k k k k k k例7：对自然数n 及一切自然数x ，求证：)].([]1[]2[]1[][苏联数学竞赛题nx nn x n x n x x =-+++++++【证明】则},{][x x x +=]1[]2[]1[][nn x n x n x x -+++++++].[]1[]2[]1[][}].{[]1}[{]2}[{]1}[{}][{.}]{[.1}{,}{11}{1}{.]1}[{]}[{]1}[{]2}[{]1}[{}][{,11}{,1}{,1,.}]{[]1}[{]2}[{]1}[{}][{}],{[][}]{][[][].1}[{]2}[{]1}[{}][{][],1}[{][]2}[{][]1}[{][}][{][]1}{][[]2}{][[]1}{][[}]{][[nx nn x n x n x x x n nn x n x n x x k n x n k n x n k n x n nk x n k x k n n n x n k x n k x n x n x x nk x n k x n k k x n nn x n x n x x x n x n x n x n nx nn x n x n x x x n n n x x n x x n x x x x n n x x n x x n x x x x =-+++++++=-+++++++-=+-<-≥<-+≥+-=-+++++-+++++++<-+≥+≤≤=-++++++++=+=-++++++++=-+++++++++++=-+++++++++++= 从而有知故知且知及由则而使设存在即可故只要证明例8：求出]31010[10020000+的个位数字.（第47届美国普特南数学竞赛试题） 【解】先找出3101010020000+的整数部分与分数部分.3101010020000+=31033103)10(100200100200200100+++- .3108110310910310310]31010[,131093103.310310,3)10(|310310|3)10(,)3(])10[(3)10(1005020000100100200001002002000100200001001001002001002002000022100100200200002210010021002100200200100+-=+-=+-=+<+=++--+---=-知显然是整数知又知其中分母的个位数字为3，分子的个位数字为9，故商的个位数字为3.。

高斯函数性质及应用高斯函数，又称为正态分布函数或钟形曲线，是数学上一种极其重要的函数形式。

它以德国数学家高斯命名，广泛应用于统计学、概率论、物理学、经济学等领域。

高斯函数具有许多重要的性质和广泛的应用。

首先，高斯函数具有对称性。

高斯函数的图像是关于其均值μ对称的，即函数的左右两边是完全一致的。

这是因为高斯函数的定义式中有(x-μ)的平方项，(x-μ)的值取正值和负值时对应的函数值是对称的。

这一特性使得高斯函数在处理对称性问题时非常有用。

其次，高斯函数的峰值出现在均值μ处。

高斯函数的峰值对应的横坐标就是函数的均值μ，即μ是高斯函数的中心位置。

这是因为高斯函数的定义式中有e的指数函数，指数函数在最值点处取最大值。

这一特性使得高斯函数在寻找数据的中心趋势时非常有用。

此外，高斯函数具有唯一的一个拐点。

当x等于均值μ时，高斯函数的斜率达到峰值的一半，这是高斯函数曲线从凹向下凸转折的点。

拐点使得高斯函数在研究曲线的凹凸性质时具有重要的参考依据。

另外，高斯函数具有无穷域的性质。

高斯函数的定义式中有e的指数函数，指数函数的定义域为负无穷到正无穷。

因此，高斯函数也具有相同的定义域，即对于实数x，高斯函数的定义是有效的，可以计算得出函数值。

这一性质使得高斯函数在推导数学模型和计算概率分布时非常方便。

在应用方面，高斯函数具有广泛的应用价值。

首先，高斯函数在统计学中常用于建模和描述数据分布。

许多自然界和社会现象都近似地符合高斯分布，例如人们的身高、IQ分数、心率等。

通过对数据进行高斯拟合，可以得到数据的均值和方差等统计特性，进而进行数据分析和决策。

其次，高斯函数在概率论中是重要的分布函数之一。

高斯函数常作为正态分布的密度函数，用于计算连续型随机变量的概率密度。

正态分布在实际问题中具有重要的应用，例如在质量控制中，高斯函数描述了产品质量分布的规律，帮助进行品质评估和质量改进。

此外，高斯函数在物理学领域也具有重要的应用。

例如，在量子力学中，高斯波包是描述粒子的一种波动模式，广泛应用于研究光束传播、粒子传导等问题。

高斯函数可视化高斯函数是一种重要的数学函数，是数理统计中经常出现的一种分布形式，它在科学计算、计算机图形学等领域有广泛的应用。

相信很多人都曾经听说过高斯函数，但是它究竟是如何运作的呢？今天，我们将通过“高斯函数可视化”来进行分步骤的解析。

一、什么是高斯函数高斯函数，又称为正态分布函数，是指在一条直线上随机分布的一组数据，这些数据呈现出一种钟形的分布形式，其中心最高，两端逐渐下降，它是一种连续分布的概率分布函数。

二、高斯函数代数式高斯函数的代数式可以表示为：$g(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$其中，$g(x)$为高斯函数的值。

$\mu$为均值，代表随机变量的期望值。

$\sigma$为标准差，它表示随机变量概率分布的离散程度，即观测值与均值之间的偏离程度。

三、高斯函数可视化为了更好地理解高斯函数，我们可以通过可视化的方式将其呈现出来，可以用Python实现。

首先，我们需要导入第三方库matplotlib，它是一个对于数据可视化很有用的工具库。

其次，我们需要定义函数g(x)，即高斯函数的值，由于高斯函数的变量是连续的，所以我们需要定义一个变量范围x，在x的范围内计算高斯函数的值：```import numpy as npimport matplotlib.pyplot as pltdef g(x, mu, sigma):return np.exp(-((x - mu)**2)/(2*(sigma**2))) /np.sqrt(2*np.pi*(sigma**2))x = np.linspace(-5, 5, num=1000)y = g(x, 0, 1)```在这个过程中，我们将变量范围定义为-5到5（num=1000表示在这个范围内分成了1000份）。

同时，我们定义了函数g(x)并且传入了两个参数：均值mu=0和标准差sigma=1。