小升初奥数试题之几何问题—附答案

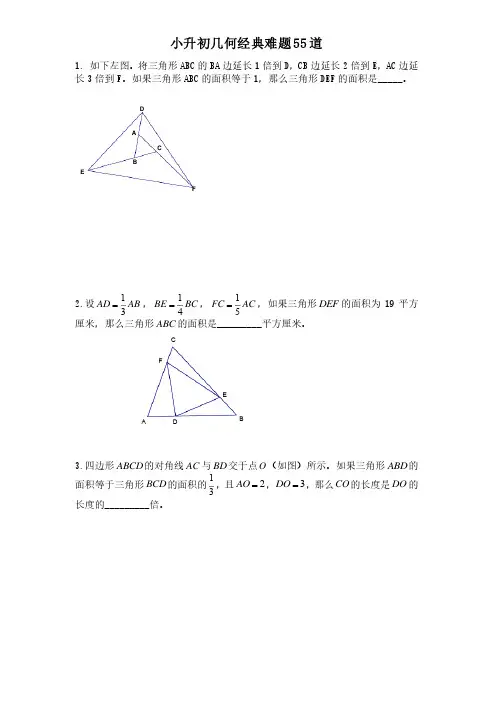
名校真题 测试卷2 （几何篇一）时间：15分钟 满分5分 姓名_________ 测试成绩_________1 （06年清华附中考题）如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.2 （06年西城实验考题）四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.3 （05年101中学考题）一块三角形草坪前，工人王师傅正在用剪草机剪草坪．一看到小灵通，王师傅热情地招呼，说：“小灵通，听说你很会动脑筋，我也想问问你，这块草坪我把它分成东、西、南、北四部分(如图)．修剪西部、东部、南部各需10分钟，16分钟，20分钟．请你想一想修剪北部需要多少分钟？4 （05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是平方厘米．5 (06年北大附中考题)三角形ABC中，C是直角，已知AC＝2，CD＝2,CB=3,AM=BM，那么三角形AMN（阴影部分）的面积为多少？【附答案】1 根据定理：ABCBED∆∆=3211⨯⨯=61，所以四边形ACDE的面积就是6-1=5份，这样三角形35÷5×6=42。

2 小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个面积和是5-1=4，所以每个三角形的面积是1，这个图形是“玄形”，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1。

3 如下所示：将北部分成两个三角形，并标上字母201016x yBACD FE那么有⎩⎨⎧++)16()10(yxS △ABG ：S △AGC ＝S △AGE ：S △GEC ＝BE ：EC ； S △BGA ：S △BGC ＝S △AGF ：S △GFC ＝AF ：FC ； S △AGC ：S △BCG ＝S △ADG ：S △DGB ＝AD ：DB ； 有时把这种比例关系称之为燕尾定理．4 四边形AFDC 的面积=三角形AFD+三角形ADC=（21×FD ×AF ）+（21×AC ×CD ）=21（FE+ED ）×AF+21 （AB+BC ）×CD= （21×FE ×AF+21×ED ×AF ）+（21×AB ×CD+21×BC ×CD ）。

周长：(高等难度）如图，把正方形ABCD的对角线AC任意分成10段，并以每一段为对角线作为正方形.设这10个小正方形的周长之和为P，大正方形的周长为L，则P与L的关系是______（填＜,＞，=）.巧求周长部分题目:(高等难度）如图,长方形ABCD中有一个正方形EFGH，且AF=16厘米，HC=13厘米,求长方形ABCD的周长是多少厘米。

年龄问题题目：（中等难度）甲、乙、丙三人年龄之和是94岁，且甲的2倍比丙多5岁,乙2倍比丙多19岁,问:甲、乙、丙三人各多大?【试题】刘老师搬一批书，每次搬15本，搬了12次，正好搬完这批书的一半。

剩下的书每次搬20本，还要几次才能搬完?【试题】小华每分拍球25次，小英每分比小华少拍5次。

照这样计算，小英5分拍多少次？小华要拍同样多次要用几分?【试题】同学们到车站义务劳动，3个同学擦12块玻璃。

(补充不同的条件求问题,编成两道不同的两步计算应用题）。

"照这样计算，9个同学可以擦多少块玻璃？”【试题】两个车间装配电视机。

第一车间每天装配35台,第二车间每天装配37台。

照这样计算，这两个车间15天一共可以装配电视机多少台？【试题】把7本相同的书摞起来，高42毫米.如果把28本这样的书摞起来,高多少毫米？(用不同的方法解答）【试题】纺织厂运来一堆煤，如果每天烧煤1500千克，6天可以烧完.如果每天烧1000千克，可以多烧几天？【试题】一台拖拉机5小时耕地40公顷，照这样的速度，耕72公顷地需要几小时1.一条路长100米，从头到尾每隔10米栽1棵梧桐树，共栽多少棵树？2.12棵柳树排成一排，在每两棵柳树中间种3棵桃树，共种多少棵桃树？一根200厘米长的木条,要锯成10厘米长的小段,需要锯几次？4.蚂蚁爬树枝，每上一节需要10秒钟，从第一节爬到第13节需要多少分钟？5。

在花圃的周围方式菊花，每隔1米放1盆花.花圃周围共20米长.需放多少盆菊花？6。

从发电厂到闹市区一共有250根电线杆,每相邻两根电线杆之间是30米。

小升初奥数真题和答案试题一：有5个亮着的灯泡，每个灯泡都由一个开关控制，每次操作可以拉动其中的2个开关以改变相应灯泡的亮暗状态，能否经过假设干次操作使得5个灯泡都变暗?解答:每个灯泡变暗需要拉动奇数次开关;那么5个灯泡全部变暗一共也需要拉动奇数次开关;而每次操作是拉动2个开关;假设干次操作后一共拉动的次数肯定是2的倍数，也就是偶数次;但是5个灯泡全部变暗一定需要总共拉动奇数次，所以矛盾了;所以无论经过多少次操作都不可能使5个灯泡一起变暗。

试题二：甲和乙两人分别从圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动，当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处又第二次相遇.求此圆形场地的周长.解答：第一次相遇时，两人合走了半个圆周;第二次相遇时，两人又合走了一个圆周，所以从第一相遇到第二次相遇时乙走的路程是第一次相遇时走的2倍，所以第二次相遇时，乙一共走了100×(2+1)=300 米，两人的总路程和为一周半，又甲所走路程比一周少60米，说明乙的路程比半周多60米，那么圆形场地的半周长为300-60=240 米，周长为240×2=480米.试题三："迎春杯"数学竞赛后，甲、乙、丙、丁四名猜想他们之中谁能获奖.甲说："如果我能获奖，那么乙也能获奖."乙说："如果我能获奖，那么丙也能获奖."丙说："如果丁没获奖，那么我也不能获奖."实际上，他们之中只有一个人没有获奖.并且甲、乙、丙说的话都是正确的.那么没能获奖的同学是。

解答：首先根据丙说的话可以推知，丁必能获奖.否那么，假设丁没获奖，那么丙也没获奖，这与"他们之中只有一个人没有获奖"矛盾。

其次考虑甲是否获奖，假设甲能获奖，那么根据甲说的话可以推知，乙也能获奖;再根据乙说的话又可以推知丙也能获奖，这样就得出4个人全都能获奖，不可能.因此，只有甲没有获奖。

小升初数学几何图形专题知识训练含答案一、单选题1．甲数和乙数的比是4∶7，甲数是乙数的（）A．47B．74C．342．甲数的14和乙数的34相等，那么甲数（）乙数。

A．大于B．小于C．等于D．不能比较3．在一张长8厘米，宽6厘米的长方形纸上，剪下一个最大的正方形，这个正方形的面积是（）。

A．36平方厘米B．48平方厘米C．64平方厘米4．下面图形都是由3个边长1厘米的小正方形组成的，其中周长最长的是（）。

A．B．C．5．旋转能得到（）A．圆柱B．圆锥C．一个空心的球6．如图，图中的物体从（）看到的形状是相同的．A．正面和上面B．正面和右面C．上面和右面7．下面运用“转化”思想方法的是（）。

A．①和②B．①和③C．②和③8．下列叙述正确的是（）A．两个数的最小公倍数是它们最大公因数的倍数。

B．三角形的底和高扩大2倍，它的面积也扩大2倍。

C．相邻两个非0的自然数，其中一定有一个是合数。

9．两个完全相同的长方形（如图），将图①和图②阴影部分的面积相比，（）A．图①大B．图②大C．图①和图②相等10．下列说法中正确的有（）。

①2厘米长的线段向上平移10厘米，线段的长还是2厘米。

②8080008000这个数只读出一个“零”。

③万级包括亿万、千万、百万、十万、万五个数位。

④三位数乘两位数，积不可能是六位数。

A．2个B．3个C．4个二、填空题11．在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆(如图).圆的直径为厘米，半径为厘米；一个圆的周长为厘米，面积为平方厘米；长方形的面积是平方厘米，阴影部分的面积是平方厘米．12．一个梯形的上底是5.8厘米，下底是6.2厘米，高是2.5厘米，它的面积是平方厘米。

13．是由几个拼成的。

；；。

14．在横线上填上“平移”或“旋转”。

汽车行驶中车轮的运动是现象；推拉门被推开是现象。

15．把一个棱长为6 cm的正方体木块削成一个最大的圆柱，圆柱的体积是，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是。

小学奥数几何题100道及答案(完整版)题目1：一个正方形的边长是5 厘米，它的面积是多少平方厘米？解题方法：正方形面积= 边长×边长，即5×5 = 25（平方厘米）答案：25 平方厘米题目2：一个长方形的长是8 分米，宽是6 分米，它的周长是多少分米？解题方法：长方形周长= （长+ 宽）×2，即（8 + 6）×2 = 28（分米）答案：28 分米题目3：一个三角形的底是10 厘米，高是6 厘米，它的面积是多少平方厘米？解题方法：三角形面积= 底×高÷2，即10×6÷2 = 30（平方厘米）答案：30 平方厘米题目4：一个平行四边形的底是12 米，高是8 米，它的面积是多少平方米？解题方法：平行四边形面积= 底×高，即12×8 = 96（平方米）答案：96 平方米题目5：一个梯形的上底是 4 厘米，下底是6 厘米，高是5 厘米，它的面积是多少平方厘米？解题方法：梯形面积= （上底+ 下底）×高÷2，即（4 + 6）×5÷2 = 25（平方厘米）答案：25 平方厘米题目6：一个圆的半径是3 厘米，它的面积是多少平方厘米？解题方法：圆的面积= π×半径²，即3.14×3²= 28.26（平方厘米）答案：28.26 平方厘米题目7：一个半圆的半径是 4 分米，它的周长是多少分米？解题方法：半圆的周长= 圆周长的一半+ 直径，即3.14×4×2÷2 + 4×2 = 20.56（分米）答案：20.56 分米题目8：一个长方体的长、宽、高分别是5 厘米、4 厘米、3 厘米，它的表面积是多少平方厘米？解题方法：长方体表面积= （长×宽+ 长×高+ 宽×高）×2，即（5×4 + 5×3 + 4×3）×2 = 94（平方厘米）答案：94 平方厘米题目9：一个正方体的棱长是6 分米，它的体积是多少立方分米？解题方法：正方体体积= 棱长³，即6³= 216（立方分米）答案：216 立方分米题目10：一个圆柱的底面半径是2 厘米，高是5 厘米，它的侧面积是多少平方厘米？解题方法：圆柱侧面积= 底面周长×高，底面周长= 2×3.14×2，即2×3.14×2×5 = 62.8（平方厘米）答案：62.8 平方厘米题目11：一个圆锥的底面半径是3 厘米，高是4 厘米，它的体积是多少立方厘米？解题方法：圆锥体积= 1/3×底面积×高，底面积= 3.14×3²，即1/3×3.14×3²×4 = 37.68（立方厘米）答案：37.68 立方厘米题目12：两个边长为4 厘米的正方形拼成一个长方形，长方形的长和宽分别是多少？面积是多少？解题方法：长方形的长为8 厘米，宽为4 厘米，面积= 8×4 = 32（平方厘米）答案：长8 厘米，宽4 厘米，面积32 平方厘米题目13：一个三角形的面积是18 平方厘米，底是6 厘米，高是多少厘米？解题方法：高= 面积×2÷底，即18×2÷6 = 6（厘米）答案：6 厘米题目14：一个平行四边形的面积是24 平方米，底是 4 米，高是多少米？解题方法：高= 面积÷底，即24÷4 = 6（米）答案：6 米题目15：一个梯形的面积是30 平方分米，上底是5 分米，下底是7 分米，高是多少分米？解题方法：高= 面积×2÷（上底+ 下底），即30×2÷（5 + 7）= 5（分米）答案：5 分米题目16：一个圆环，外圆半径是5 厘米，内圆半径是 3 厘米，圆环的面积是多少平方厘米？解题方法：圆环面积= 外圆面积-内圆面积，即 3.14×（5²- 3²）= 50.24（平方厘米）答案：50.24 平方厘米题目17：一个长方体的棱长总和是48 厘米，长、宽、高的比是3:2:1，长方体的体积是多少立方厘米？解题方法：一条长、宽、高的和为48÷4 = 12 厘米，长为6 厘米，宽为4 厘米，高为2 厘米，体积= 6×4×2 = 48（立方厘米）答案：48 立方厘米题目18：一个正方体的表面积是54 平方分米，它的一个面的面积是多少平方分米？解题方法：一个面的面积= 表面积÷6，即54÷6 = 9（平方分米）答案：9 平方分米题目19：一个圆柱的底面直径是4 分米，高是3 分米，它的表面积是多少平方分米？解题方法：底面积= 3.14×（4÷2）²= 12.56 平方分米，侧面积= 3.14×4×3 = 37.68 平方分米，表面积= 2×12.56 + 37.68 = 62.8（平方分米）答案：62.8 平方分米题目20：一个圆锥的底面周长是18.84 分米，高是5 分米，它的体积是多少立方分米？解题方法：底面半径= 18.84÷3.14÷2 = 3 分米，体积= 1/3×3.14×3²×5 = 47.1（立方分米）答案：47.1 立方分米题目21：一个长方体的水箱，长 5 分米，宽4 分米，高 3 分米，里面装满水，把水倒入一个棱长为5 分米的正方体水箱，水深多少分米？解题方法：水的体积= 5×4×3 = 60 立方分米，正方体水箱底面积= 5×5 = 25 平方分米，水深= 60÷25 = 2.4 分米答案：2.4 分米题目22：一块长方形的铁皮，长8 分米，宽6 分米，从四个角各切掉一个边长为1 分米的正方形，然后做成一个无盖的盒子，这个盒子的容积是多少立方分米？解题方法：盒子长6 分米，宽4 分米，高1 分米，容积= 6×4×1 = 24（立方分米）答案：24 立方分米题目23：一个圆柱的体积是60 立方厘米，底面积是12 平方厘米，高是多少厘米？解题方法：高= 体积÷底面积，即60÷12 = 5（厘米）答案：5 厘米题目24：一个圆锥和一个圆柱等底等高，圆柱的体积是27 立方分米，圆锥的体积是多少立方分米？解题方法：等底等高的圆锥体积是圆柱体积的1/3，即27×1/3 = 9（立方分米）答案：9 立方分米题目25：把一个棱长为 6 厘米的正方体铁块熔铸成一个底面积为36 平方厘米的圆柱体，这个圆柱体的高是多少厘米？解题方法：正方体体积= 6³= 216 立方厘米，圆柱体的高= 体积÷底面积，即216÷36 = 6（厘米）答案：6 厘米题目26：一个直角三角形的两条直角边分别是3 厘米和4 厘米，斜边是5 厘米，这个三角形的面积是多少平方厘米？解题方法：直角三角形面积= 两条直角边乘积的一半，即3×4÷2 = 6（平方厘米）答案：6 平方厘米题目27：一个等腰三角形的周长是20 厘米，其中一条腰长8 厘米，底边长多少厘米？解题方法：等腰三角形两腰相等，所以底边长= 周长-腰长×2，即20 - 8×2 = 4（厘米）答案：4 厘米题目28：一个扇形的圆心角是90°，半径是6 厘米，这个扇形的面积是多少平方厘米？解题方法：扇形面积= 圆心角÷360°×圆的面积，即90÷360×3.14×6²= 28.26（平方厘米）答案：28.26 平方厘米题目29：一个长方体的底面是边长为5 厘米的正方形，高是8 厘米，这个长方体的体积是多少立方厘米？解题方法：长方体体积= 底面积×高，底面积= 5×5 = 25 平方厘米，体积= 25×8 = 200（立方厘米）答案：200 立方厘米题目30：一个圆柱的底面周长是18.84 厘米，高是10 厘米，它的体积是多少立方厘米？解题方法：底面半径= 18.84÷3.14÷2 = 3 厘米，体积= 3.14×3²×10 = 282.6（立方厘米）答案：282.6 立方厘米题目31：一个圆锥的底面直径是8 厘米，高是6 厘米，它的体积是多少立方厘米？解题方法：底面半径= 8÷2 = 4 厘米，体积= 1/3×3.14×4²×6 = 100.48（立方厘米）答案：100.48 立方厘米题目32：把一个棱长为8 厘米的正方体木块削成一个最大的圆柱，这个圆柱的体积是多少立方厘米？解题方法：圆柱的底面直径和高都是8 厘米，体积= 3.14×（8÷2）²×8 = 401.92（立方厘米）答案：401.92 立方厘米题目33：一个长方体玻璃缸，从里面量长4 分米，宽 3 分米，高5 分米，缸内水深2.5 分米。

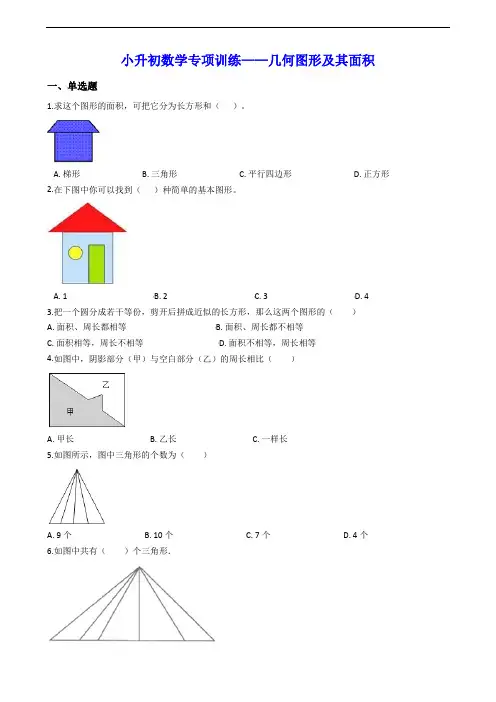
小升初数学专项训练——几何图形及其面积一、单选题1.求这个图形的面积，可把它分为长方形和（）。

A. 梯形B. 三角形C. 平行四边形D. 正方形2.在下图中你可以找到（）种简单的基本图形。

A. 1B. 2C. 3D. 43.把一个圆分成若干等份，剪开后拼成近似的长方形，那么这两个图形的（）A. 面积、周长都相等B. 面积、周长都不相等C. 面积相等，周长不相等D. 面积不相等，周长相等4.如图中，阴影部分（甲）与空白部分（乙）的周长相比（）A. 甲长B. 乙长C. 一样长5.如图所示，图中三角形的个数为（）A. 9个B. 10个C. 7个D. 4个6.如图中共有（）个三角形．A. 5B. 20C. 157.一个5边形的三个内角是直角，另外两个角相等，那么这两个角的度数是（）。

A. 100°B. 120°C. 135°二、判断题8.105厘米＞1米．9.100厘米比1米长．10. 1米的线段比100厘米的线段长。

11.梯形的内角和是180°。

（）12.任意四边形的内角和都是360°．三、填空题13.如图，CD=15厘米，AE=16厘米．AB﹣BC=1厘米，则三角形ABC的面积是________ 平方厘米．14.把棱长为1分米的正方体表面涂上红色后，再把它分成棱长为1厘米的小正方体．小正方体中只有一面涂色的有________ 个．15.如图，已知三角形ABC中，BD：DC=3：2，E是AD的中点，阴影部分的面积是13.5平方分米，三角形ABC的面积是________ 平方分米16.把这个物体放到地面上，观察并填空。

是由________个小正方体拼成的。

如果把这个图形的表面涂上绿色，不涂色的有________个小正方体；一个面涂绿色的有________个小正方体；有2个面涂绿色的有________个小正方体；有3个面涂绿色的有________个小正方体；有4个面涂绿色的有________个小正方体；有5个面涂红色的有________个小正方体。

小升初几何应用题数学
小升初是一个重要的学习阶段，学生需要掌握许多基础知识，包括几何学。

以下是一个简单的几何应用题，适合小升初的学生解答。

题目：有一个正方形花坛，其边长为8米。

一只蜗牛从花坛的角落开始爬行，它每分钟爬行2米。

问题是：蜗牛需要多长时间才能完全爬出这个花坛？
解题思路：
1. 首先，我们需要确定蜗牛要完全爬出花坛的总距离。

由于花坛是一个正方形，边长为8米，蜗牛需要爬出4个边才能完全离开。

所以，总距离是4 × 8 = 32 米。

2. 接下来，我们需要将总距离除以蜗牛每分钟爬行的速度来计算所需的时间。

因此，时间 = 总距离÷ 速度 = 32 米÷ 2 米/分钟 = 16 分钟。

所以，蜗牛需要16分钟才能完全爬出这个花坛。

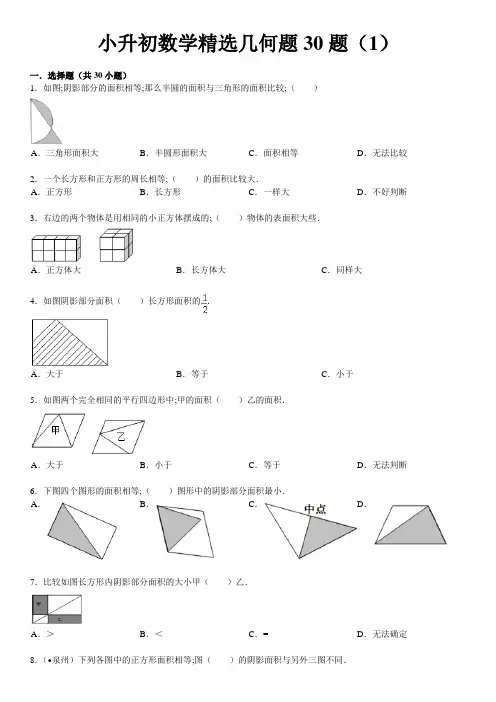
小升初数学精选几何题30题（1）一．选择题（共30小题）1．如图;阴影部分的面积相等;那么半圆的面积与三角形的面积比较;（）A．三角形面积大B．半圆形面积大C．面积相等D．无法比较2．一个长方形和正方形的周长相等;（）的面积比较大．A．正方形B．长方形C．一样大D．不好判断3．右边的两个物体是用相同的小正方体摆成的;（）物体的表面积大些．A．正方体大B．长方体大C．同样大4．如图阴影部分面积（）长方形面积的．A．大于B．等于C．小于5．如图两个完全相同的平行四边形中;甲的面积（）乙的面积．A．大于B．小于C．等于D．无法判断6．下图四个图形的面积相等;（）图形中的阴影部分面积最小．A．B．C．D．7．比较如图长方形内阴影部分面积的大小甲（）乙．A．＞B．＜C．=D．无法确定8．（•泉州）下列各图中的正方形面积相等;图（）的阴影面积与另外三图不同．A．B．C．D．9．如图中的涂色部分是连接梯形的顶点和边的中点形成的．涂色部分的面积不等于所在梯形面积的是（）A．B．C．D．10．如图所示;比较A和B的面积大小;其结果是（）A．S A＞S B B．S A＜S BC．S A=S B D．条件不够;不能确定11．右面方格图中有A、B两个三角形;那么（）A．A的面积大B．B的面积大C．A、B的面积一样大D．无法确定12．用两根同样长的铁丝分别围成一个长方形和一个正方形;这两个图形的面积相比（）A．正方形大B．长方形大C．一样大D．无法确定13．一个长方形的长增加;宽缩短;这个长方形的面积与原来面积相比（）A．不变B．增加了C．减少了D．减少14．如图所示的正方形的边长都是2厘米;阴影部分的面积相等的有（）A．①②③B．②③④C．①②③④D．①③④15．如图：两个相同的圆锥容器;水深都是圆锥高的一半;那么甲容器中水的体积是乙容器中水的体积的（）倍．A．2B．3C．7D．16．一个圆锥体的体积是4.5立方分米;高是0.9分米;它的底面积是（）A．1.35平方分米B．15平方分米C．5平方分米D．平方分米17．如图中;两个小圆面积之和占大圆面积的（）（最小圆半径为1;最大的圆的半径为3）A．B．C．D．18．下面三平面图形中的阴影部分;面积最小的是（）A．B．C．19．如图;平行四边形ABCD的底BC长是12厘米;线段FE长是4厘米;那么平行四边形中的阴影部分面积是（）平方厘米．A．24 B．36 C．48 D．7220．如图．一个平行四边形相邻两条边长度分别是4厘米和8厘米;其中一条底边上的高是6厘米;这个平行四边形的面积是（）A．24平方厘米B．48平方厘米C．32平方厘米21．一个周长为20cm的长方形;如果把它的长减少1cm;宽增加1cm;那么它变成一个正方形;则原长方形的面积是（）cm2．A．30 B．25 C．40 D．2422．如图所示;四边形ABCD是长方形;图中甲、乙也是长方形;已知甲的面积是10平方厘米;乙的面积是（）A．10 B．8C．6D．523．周长相等的正方形和圆;其面积的比是（）A．π：4 B．4：πC．1：1 D．2：324．如图;有两枚硬币A和B;硬币A的半径是硬币B半径的2倍;将硬币A固定在桌面上;硬币B绕硬币A无滑动地滚动一周;则硬币B自转的圈数是（）A．1圈B．1.5圈C．2圈D．3圈25．一个钟表的分针长10厘米;从2时走到5时;分针针尖走过了（）厘米．A．31.4 B．62.8 C．15.7 D．188.426．（•恩施州）图中共有（）个长方形．A．30 B．28 C．26 D．2427．（•）将棱长2厘米的小正方体按如图方式摆放在地上;露在外面的面的面积是（）厘米2．A．24 B．48 C．96 D．12828．（•）一个棱长3分米的正方体的表面涂满了红色;将它切成棱长1分米的小正方体．三面涂色的小正方体有（）个．A．12 B．8C．6D．129．在图中一共有（）个三角形．A．9B．10 C．1130．图中共有（）个三角形．A．25 B．27 C．29 D．36小升初几何卷2参考答案与试题解析一．选择题（共30小题）1．如图;阴影部分的面积相等;那么半圆的面积与三角形的面积比较;（）A．三角形面积大B．半圆形面积大C．面积相等D．无法比较考点：面积及面积的大小比较．分析：利用等量代换;为了便于分析;可以把图形中的各部分标上序号;如下图：已知阴影部分的面积相等;即图①=图②;图①+图③=半圆的面积;图②+图③=三角形的面积;图③是公共部分;由此问题得到解决．解答：解：如图：已知阴影部分的面积相等;即图①=图②;又因为图①+图③=半圆的面积;图②+图③=三角形的面积;图③是公共部分;所以半圆的面积与三角形的面积相等．故选：C．点评：此题主要利用等量代换的方法来解决问题．2．一个长方形和正方形的周长相等;（）的面积比较大．A．正方形B．长方形C．一样大D．不好判断考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：正方形和长方形的周长相等;正方形的面积比长方形的面积大．可以通过举例证明;如它们的周长都是24厘米;长方形的长是8厘米;宽是4厘米;正方形的边长是6厘米;利用各自的面积公式;求出面积;比较后即可进行判断．解答：解：设它们的周长都是24厘米;长方形的长是8厘米;宽是4厘米;正方形的边长是6厘米;长方形的面积：8×4=32（平方厘米）;正方形的面积：6×6=36（平方厘米）;答：周长相等的正方形和长方形;正方形的面积大．故选：A．点评：此题主要考查周长相等的正方形和长方形的面积大小的比较;明确正方形的面积大．3．右边的两个物体是用相同的小正方体摆成的;（）物体的表面积大些．A．正方体大B．长方体大C．同样大考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：我们假设小正方体的棱长是1;由此分别求出正方体与长方体的表面积即可;再进行选择．解答：解：正方体的表面积：2×2×6=24;长方体的表面积：（4×1+4×2+1×2）×2;=（4+8+2）×2;=28;长方体的表面积大些;故应选：B．点评：本题运用正方体;长方体的表面积公式进行解答即可．4．如图阴影部分面积（）长方形面积的．A．大于B．等于C．小于考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：如图;连接AC;三角形ACD的高与长方形的宽相等;三角形的底边等于长方形的长;由此即可得出三角形ACD 的面积与长方形面积之间的关系;进一步推出阴影部分面积与长方形面积之间的关系．解答：解：连接AC;S△ACD=S四边形ECDF;所以S△ACD+S△ABC＞S四边形ECDF;即阴影部分面积大于长方形面积的;故选：A．点评：考查了三角形的面积;长方形的面积．本题得到三角形的高与长方形的宽相等以及三角形的底等于长方形的长;从而求出三角形与长方形面积之间的关系;进一步解决问题．5．如图两个完全相同的平行四边形中;甲的面积（）乙的面积．A．大于B．小于C．等于D．无法判断考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：根据题意可知;两个完全相同的平行四边形;甲的面积和乙的面积都是这个平行四边形面积的一半;所以它们的面积相等．解答：解：甲的面积和乙的面积都是这个平行四边形面积的一半;所以它们的面积相等．故选：C．点评：解答本题的关键是根据图形找出三角形面积与平行四边形的面积的关系;可知三角形面积等于平行四边形面积的;进而用等量代换的方法解决．6．下图四个图形的面积相等;（）图形中的阴影部分面积最小．A．B．C．D．考点：面积及面积的大小比较;三角形的周长和面积．分析：已知这四个图形的面积相等;A图形阴影部分的面积是A 图形面积的;B图形的阴影部分面积是比B图形面积的少;C图形的阴影部分面积是B 图形面积的;D图形的阴影部分面积比D 图形面积的多．可以知道B 图形中的阴影部分面积最小．解答：解：A图形是个长方形;对角线把长方形面积分成相等的两部分;A图形阴影部分的面积等于图形面积的一半;B图形的面积小于图形面积的一半;C图阴影部分的面积等于图形面积的一半;DD图形的阴影部分面积比D图形面积的一半要多．可以知道B图形中的阴影部分面积最小．故选：B．点评：本题是一道面积大小的比较题;考查了学生观察能力;比较分析的能力．7．比较如图长方形内阴影部分面积的大小甲（）乙．A．＞B．＜C．=D．无法确定考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：如图：在三角形中;等底等高的两个三角形的面积相等;所以面积1=面积2;面积3等于面积4;面积甲=面积乙．解答：解：因为面积1=面积2;面积3等于面积4;所以面积甲=面积乙．故选：C．点评：解答此题的关键是根据等底等高的两个三角形的面积相等进行分析即可．8．（•泉州）下列各图中的正方形面积相等;图（）的阴影面积与另外三图不同．A．B．C．D．考点：组合图形的面积．专题：平面图形的认识与计算．分析：从图中可以看出阴影部分的面积=正方形的面积﹣圆的面积．观察图形可发现：四个正方形是全等的;面积是相等;A、C、D三个图形中空白部分可以组成一个完整的圆;根据圆的面积相等可得这三个图形中阴影部分的面积相等;得出答案．解答：解：由图可知：从左到右A、C、D的空白处均可组成一个完整的半径相等的圆;而正方形的面积相等;根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等．故选：B．点评：此题考查了面积及等积变换;将阴影面积转化为易求的图形的面积的差或和是解题的常用方法．9．如图中的涂色部分是连接梯形的顶点和边的中点形成的．涂色部分的面积不等于所在梯形面积的是（）A．B．C．D．考点：面积及面积的大小比较．分析：要判断涂色部分的面积是否等于梯形面积的;需要根据梯形的面积公式和三角形的面积公式;计算出涂色部分的面积;再与梯形的面积进行比较;确定选择哪个选项．解答：解：梯形的上底用a表示;下底用b表示;高用h表示．A、空白部分是四个三角形;上面两个三角形的底是梯形上底的;高是梯形的高的;则上面两个三角形的面积和为：×a ×h×2=ah;下面两个三角形的底是梯形下底的;高是梯形的高的;则下面两个三角形的面积和为：×b ×h×2=bh;空白部分的面积为：ah+bh=（a+b）h;梯形的面积为：（a+b）h;涂色部分的面积等于梯形的面积﹣空白部分的面积;故涂色部分的面积为：（a+b）h;是梯形面积的;B、空白部分是三个三角形;上面的三角形面积为：ah;下面两个三角形面积和为：bh;空白部分的面积为：ah+bh=（a+b）h;梯形的面积为：（a+b）h;涂色部分的面积等于梯形的面积﹣空白部分的面积;故涂色部分的面积为：（a+b）h;是梯形面积的;C、空白部分左面的三角形面积为：ah;右面两个三角形的面积和为：ah+bh;空白部分的面积为：ah+bh;故涂色部分的面积为：ah+bh;不是梯形面积的;D、涂色部分是梯形;它的上底是a;下底是b;高是h;涂色部分的面积=（a+b）h;是梯形面积的．故选：C．点评：解答此题关键是根据梯形的面积公式和三角形的面积公式;计算出涂色部分的面积;再确定涂色部分的面积是否等于梯形面积的;最后确定选择哪个选项．10．如图所示;比较A和B的面积大小;其结果是（）A．S A＞S B B．S A＜S BC．S A=S B D．条件不够;不能确定考点：面积及面积的大小比较．分析：根据题意为了便于表示;添加了两个字母如下图和假设圆的直径是4厘米;要比较A和B的面积大小;需要分别求出A和B的面积由题意可求S A=半圆的面积﹣弧形ADF的面积;S B利用三角形的面积直接计算;进而比较出大小．解答：解：设圆的直径是4厘米;由题意和面积公式得三角形的DEF的面积=4×（4÷2）÷2=EF2÷2=4（平方厘米）;弧形ADF的面积=3.14×EF2×﹣4=3.14×（4×2）×﹣4=6.28﹣4=2.28（平方厘米）;S A=（4÷2）2×3.14÷2﹣2.28=6.28﹣2.28=4（平方厘米）;因为4=4;所以S A=S B;故选：C．点评：此题考查了组合图形的面积;解题关键是看懂图示和求出弧形的面积;根据图形中半圆的面积、三角形的面积与弧形ADF的面积的关系;列式解答．11．右面方格图中有A、B两个三角形;那么（）A．A的面积大B．B的面积大C．A、B的面积一样大D．无法确定考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：由题意可知：两个三角形同底;但高不能确定;根据三角形面积=底×高÷2可知：两个三角形的面积大小无法确定;据此判断．解答：解：如图;A、B两个三角形有公共底边MN;该底边对应的高不一定相等;由三角形的面积公式：s=ah÷2;可知A、B的面积大小无法确定．故选：D．点评：考查了三角形的面积及面积的大小比较;明确三角形的面积计算方法是解答此题的关键．12．用两根同样长的铁丝分别围成一个长方形和一个正方形;这两个图形的面积相比（）A．正方形大B．长方形大C．一样大D．无法确定考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：设铁丝的长度为20厘米;长方形的长和宽分别为6厘米和4厘米;则正方形的边长为5厘米;利用长方形的面积公式分别求其面积;即可比较面积的大小．解答：解：设铁丝的长度为20厘米;长方形的长和宽分别为6厘米和4厘米;则正方形的边长为5厘米;长方形的面积=6×4=24（平方厘米）;正方形的面积=5×5=25（平方厘米）;正方形的面积＞长方形的面积;故选：A．点评：利用周长相等;举例分别求出长方形和正方形的面积即可解答．13．一个长方形的长增加;宽缩短;这个长方形的面积与原来面积相比（）A．不变B．增加了C．减少了D．减少考点：面积及面积的大小比较;长方形、正方形的面积．分析：可以设这个长方形的长为20厘米;宽为10厘米;然后分别计算长方形的现在的面积和原来的面积后进行解答即可．解答：解：原来的面积：20×10=200（平方厘米）;现在的长：20×（1+）=22（厘米）;宽：10×（1﹣）=9（厘米）;现在的面积：22×9=198（平方厘米）;所以比原来减少了：（200﹣198）÷200=;故选：C．点评：此题主要考查了长方形的面积和求一个数比另一个数多（或少）几分之几的综合应用．14．如图所示的正方形的边长都是2厘米;阴影部分的面积相等的有（）A．①②③B．②③④C．①②③④D．①③④考点：面积及面积的大小比较．专题：平面图形的认识与计算．分析：通过仔细观察;每个图形中正方形的边长是2厘米;圆的半径是1厘米;阴影部分的面积等于正方形面积减去一个圆的面积;因此得解．解答：解：①4个半径是1厘米的圆;合起来是一个整圆;阴影部分面积=2厘米×2厘米﹣π×1厘米2;②阴影部分面积=正方形面积﹣圆的面积=2厘米×2厘米﹣π×1厘米2;③两个半径1厘米的半圆合起来是一个整圆;阴影部分面积=正方形面积﹣圆面积=2厘米×2厘米﹣π×1厘米2;④4个半径是1厘米的圆;合起来是一个整圆;阴影部分面积=2厘米×2厘米﹣π×1厘米2;所以阴影部分的面积相等的有①②③④;故选：C．点评：看明白图形是解决此题的关键．15．如图：两个相同的圆锥容器;水深都是圆锥高的一半;那么甲容器中水的体积是乙容器中水的体积的（）倍．A．2B．3C．7D．考点：圆锥的体积．专题：立体图形的认识与计算．分析：此题可以通过圆锥的体积公式求出水的体积;然后再用甲容器内水的体积除以乙容器内水的体积即可．再求水的体积和整个圆锥容器的容积时;可以设出水的半径和高度;那么圆锥容器的半径和高度分别是水的2倍;然后利用圆锥的体积公式解答．解答：解：设圆锥的底面半径为2r;高为2h;甲圆锥内水的体积为：π（2r）2×2h﹣πr2h=πr2h;乙圆锥内水的体积为：πr2h;甲容器内水的体积是乙容器内水的体积的：πr2h÷πr2h=7;答：甲容器中水的体积是乙容器中水的体积的7倍．故选：C．点评：此题主要考查的是圆锥体积公式的灵活应用．16．一个圆锥体的体积是4.5立方分米;高是0.9分米;它的底面积是（）A．1.35平方分米B．15平方分米C．5平方分米D．平方分米考点：圆锥的体积．分析：根据圆锥的体积公式;底面积等于体积除以除以高;列式解答即可得到答案．解答：解：4.5÷÷0.9=15（平方分米）;故选：B．点评：此题主要考查的是圆锥的体积公式的应用．17．如图中;两个小圆面积之和占大圆面积的（）（最小圆半径为1;最大的圆的半径为3）A．B．C．D．考点：圆、圆环的面积．分析：根据题意;可用最大圆的直径减去最小圆的直径得到中等圆的直径;再计算出中等于的半径;最后根据圆的面积公式计算出这三个圆的面积;再用两个小圆的面积之和比上大圆的面积即可得到答案．解答：解：中等圆的半径为：（3×2﹣1×2）÷2=（6﹣2）÷2;=4÷2;=2;（3.14×12+3.14×22）÷3.14×32=（3.14+12.56）÷28.26;=15.7÷28.26;=;答：两个小圆的面积之和占大圆面积的．故答案为：C．点评：解答此题的关键是确定中等圆的半径;然后再根据圆的面积公式进行计算即可．18．下面三平面图形中的阴影部分;面积最小的是（）A．B．C．分析：可根据圆的面积公式S=πr2和圆环的面积公式=π（大圆的半径）2﹣（小圆半径的平方）2π;列式计算后再比较大小即可得到答案．解答：解：A：3.14×÷2=50.24÷2;=25.12;B：3.14×=28.26;C：3.14×﹣3.14×;=50.24﹣28.26;=21.98;所以A＞B＞C;即面积最小的是图形C．故答案为：C．点评：此题主要考查的是圆、圆环的面积公式的灵活应用．19．如图;平行四边形ABCD的底BC长是12厘米;线段FE长是4厘米;那么平行四边形中的阴影部分面积是（）平方厘米．A．24 B．36 C．48 D．72考点：平行四边形的面积;三角形的周长和面积．分析：先求出三角形BFC的面积;因为两个空白三角形的面积相等;所以△GBC与△CAD的面积相等;都是平行四边形ABCD面积的一半;而△GFC是公共部分;所以△FAG与△CGD的面积之和与△FBC的面积相等;从而可以求出阴影部分的面积．解答：解：因为△FAG与△CGD的面积之和与△FBC的面积相等;所以阴影部分的总面积是：12×4÷2×2;=48÷2×2;=48（平方厘米）．答：阴影部分的面积是48平方厘米．故选：C．点评：解答此题的关键是：弄清楚三个阴影三角形面积大小的关系．20．如图．一个平行四边形相邻两条边长度分别是4厘米和8厘米;其中一条底边上的高是6厘米;这个平行四边形的面积是（）A．24平方厘米B．48平方厘米C．32平方厘米分析：根据题意可知;平行四边形的底为8厘米时;高不可能为6厘米;因为高是两条平行线内最短的线段;所以这个平行四边形的底应该为4厘米;高是6厘米;那么根据平行四边形的面积=底×高计算即可得到答案;其中平行四边形的边长8厘米不参与计算．解答：解：4×6=24（平方厘米）;答：平行四边形的面积是24平方厘米．故选：A．点评：解答此题的关键是确定平行四边形的高是对应的哪条底;然后再根据平行四边形的面积公式进行计算即可．21．一个周长为20cm的长方形;如果把它的长减少1cm;宽增加1cm;那么它变成一个正方形;则原长方形的面积是（）cm2．A．30 B．25 C．40 D．24考点：长方形、正方形的面积．专题：平面图形的认识与计算．分析：周长为20厘米;则长与宽的和是20÷2=10（厘米）;则这个长方形可能是（由题意得组成的正方形除外）：长9厘米;宽1厘米;长8厘米;宽2厘米;长7厘米;宽3厘米;长6厘米;宽4厘米;又因为把它的长减少1cm;宽增加1cm;那么它变成一个正方形;所以这个长方形为：长6厘米;宽4厘米;根据面积公式计算即可．解答：解：20÷2=10（厘米）;又因为把它的长减少1cm;宽增加1cm;那么它变成一个正方形;所以这个长方形为：长6厘米;宽4厘米;则原长方形的面积是：6×4=24（平方厘米）．答：原长方形的面积是24平方厘米．故选：D．点评：解决本题的关键是根据题意推导出原长方形的长与宽;再代入公式计算．22．如图所示;四边形ABCD是长方形;图中甲、乙也是长方形;已知甲的面积是10平方厘米;乙的面积是（）A．10 B．8C．6D．5考点：长方形、正方形的面积．专题：平面图形的认识与计算．分析：如图;长方形ABCD被对角线分成两个相等的三角形;而三角形a和三角形b的面积相等;三角形c和三角形d 的面积相等;所以三角形甲、乙的面积是相等的．解答：解：因为长方形ABCD被对角线分成两个相等的三角形;而三角形a和三角形b的面积相等;三角形c和三角形d的面积相等;所以三角形甲、乙的面积是相等的．即乙的面积是10平方厘米;故选：A．点评：关键是根据题意与图形;得出三角形之间的面积的关系;进而得出要求的长方形的面积与甲的面积的关系．23．周长相等的正方形和圆;其面积的比是（）A．π：4 B．4：πC．1：1 D．2：3考点：长方形、正方形的面积;比的意义;圆、圆环的面积．专题：平面图形的认识与计算．分析：设周长是C;则正方形的边长是;圆的半径是;根据它们的面积公式求出它们的面积;写出对应的比;再化简即可．解答：解：设周长是C;则正方形的边长是;圆的半径是;则圆的面积为：××π=;正方形的面积为：×=;则正方形的面积：圆的面积=：=π：4．故选：A．点评：本题主要是灵活利用正方形和圆的周长公式与面积公式解决问题．24．如图;有两枚硬币A和B;硬币A的半径是硬币B半径的2倍;将硬币A固定在桌面上;硬币B绕硬币A无滑动地滚动一周;则硬币B自转的圈数是（）A．1圈B．1.5圈C．2圈D．3圈考点：圆、圆环的周长．分析：设A硬币的半径为2r;B硬币的半径为r;那么B硬币的运动轨迹同样是圆;但是B硬币运动轨迹的圆的半径为2r+r=3r（因为它是绕着A硬币的圆心为圆心进行运动的）;B硬币运动一周的周长为2πr;而第二枚硬币B 的周长为：2π×（2r+r）=6πr;进而用6πr除以2πr即可．解答：解：设硬币B的半径为r;则硬币A的半径为2r;[2π（2r+r）]÷（2πr）;=[6πr]÷（2πr）;=3（圈）;答：硬币B自转的圈数是3圈．故选：D．点评：此题考查了圆的周长的计算方法;应结合实际;灵活运用．25．一个钟表的分针长10厘米;从2时走到5时;分针针尖走过了（）厘米．A．31.4 B．62.8 C．15.7 D．188.4考点：圆、圆环的周长．分析：分针长10厘米等于半径;一小时分针绕圆盘一圈;根据“圆的周长=2πr”求出一圈的长（周长）;然后乘3解答即可．解答：解：2×3.14×10×（5﹣2）;=62.8×3;=188.4（厘米）;故选：D．点评：此题考查圆的周长的计算方法;应明确周长和半径、直径之间的关系;进行解答即可．26．（•恩施州）图中共有（）个长方形．A．30 B．28 C．26 D．24考点：组合图形的计数．专题：几何的计算与计数专题．分析：根据长边的线段上有5个点;得出线段的条数为10条;短边的线段有3个点;得出线段的条数为3条;从而得出长方形的个数．解答：解：因为长边的线段上有5个点;得出线段的条数为10条;短边的线段有3个点;得出线段的条数为3条;长方形的个数为：10×3=30（个）;故选：A．点评：利用点分成线段条数得出长方形个数;从而求出长方形的个数;题目有一定抽象性;应认真分析;从而确定解题思路．27．（•）将棱长2厘米的小正方体按如图方式摆放在地上;露在外面的面的面积是（）厘米2．A．24 B．48 C．96 D．128考点：规则立体图形的表面积;从不同方向观察物体和几何体．专题：立体图形的认识与计算．分析：从前、后面看露在外面的共有12个边长2厘米的正方形的面;从上面看露在外面的有6个正方形的面;从侧面看露在外面的共有6个正方形的面;此立体图形露在外面的面的总个数为：12+6+6=24个;先求出一个正方形面的面积;进而求得24个正方形面的总面积;解答：解：露在外面的总面数：12+6+6=24（个）;一个正方形面的面积：22=4（平方厘米）;立体图形的总面积：4×24=96（平方厘米）;故答案为：C．点评：此题考查规则立体图形的表面积;解决此题关键是先求出露在外面的正方形面的个数;再求得一个正方形面的面积;进而求得总面积;28．（•）一个棱长3分米的正方体的表面涂满了红色;将它切成棱长1分米的小正方体．三面涂色的小正方体有（）个．A．12 B．8C．6D．1考点：染色问题．专题：传统应用题专题．分析：棱长为3分米的正方体分割为边长是1分米的小正方体;每条棱上能分成3÷1=3（个）;根据切割特点;三面涂色的小正方体处在8个顶点上;两面涂色的处在每条棱的中间;一面涂色的处在每个面的中间;据此解答．解答：解：根据切割特点;只有在顶点上的小正方体才有三个面露在外面;所以三面涂色的小正方体处在8个顶点上;所以三面涂色的小正方体有8个．故选：B．点评：本题应在明确能分成几个小正方体的基础上;得出三种不同小正方体所处的位置是本题的解答难点．。

数学奥数几何竞赛试题及答案试题一：题目：在直角三角形ABC中，∠C=90°，AB是斜边，BC=6厘米，AC=8厘米。

求三角形ABC的面积。

答案：根据直角三角形的面积公式，面积S = (底× 高) / 2。

这里，底BC=6厘米，高AC=8厘米。

所以，S = (6 × 8) / 2 = 48 / 2 = 24平方厘米。

试题二：题目：一个圆的半径为5厘米，求这个圆的周长和面积。

答案：圆的周长公式为C = 2πr，其中r是圆的半径。

将半径r=5厘米代入公式，得C = 2 × π ×5 = 10π ≈ 31.4厘米。

圆的面积公式为A = πr²，将半径r=5厘米代入公式，得A = π × 5² = 25π ≈ 78.5平方厘米。

试题三：题目：一个正六边形的边长为a厘米，求这个正六边形的周长和面积。

答案：正六边形的周长等于6倍边长，所以周长P = 6a厘米。

正六边形可以被划分为6个等边三角形，每个等边三角形的面积为(√3/4)a²。

所以，正六边形的面积A = 6 × (√3/4)a² = (3√3/2)a²平方厘米。

试题四：题目：在一个长方体中，如果长、宽、高分别为l、w、h，求这个长方体的表面积和体积。

答案：长方体的表面积A = 2(lw + lh + wh)。

长方体的体积V = lwh。

试题五：题目：在一个等腰三角形中，如果底边长度为10厘米，两腰的长度相等，且底角为45°，求两腰的长度。

答案：由于底角为45°，我们可以知道这是一个等腰直角三角形。

在等腰直角三角形中，两腰相等，且是底边的√2倍。

所以，两腰的长度为10 × √2 ≈ 14.14厘米。

结束语：以上是本次数学奥数几何竞赛的试题及答案，希望同学们能够通过这些题目加深对几何知识的理解，并在竞赛中取得优异的成绩。

2022年小升初名校奥数专题训练：几何一、填空题（共5小题）1．如图，ABCD是边长为10厘米的正方形，且AB是半圆的直径，则阴影部分的面积是平方厘米．（π取3.14）2．如图边长为4的正方形ABCD和边长为6的正方形BEFG并排放在一起，O1和O2分别是两个正方形的中心（正方形对角线的交点），则阴影部分的面积是．3．如图，正方形ABCD的边长是5厘米，点E、F分别是AB和BC的中点，EC与DF交于点G，则四边形BEGF的面积等于平方厘米．4．如图所示的四个正方形的边长都是1，图中的阴影部分的面积依次用S1，S2，S3，S4表示，则S1，S2，S3，S4从小到大排列依次是．5．手工课上，小红用一张直径是20cm的圆形纸片剪出如图所示的风车图案（空白部分），则被剪掉的纸片（阴影部分）的面积是cm2．（π取3.14）二、解答题（共16小题）6．A、B两点分别是长方形的长和宽的中点，那么，阴影部分（如图）占长方形面积的（填几分之几）．7．在如图的梯形中，A，M，N分别为所在线段的中点，阴影部分面积为15cm2，求梯形的面积．8．如图由两个相同的梯形重叠在一起，求图中阴影部分的面积．（单位：厘米）9．如图所示的大正方形的边长是10cm，求阴影部分的面积．10．如图是由直径分别为4cm，6cm和10cm的三个半圆所组成的图形，求图中阴影部分的面积．（π取3.14）11．将16个相同的小正方体拼成一个体积为16的长方体，表面涂上漆，然后分开，则3个面涂漆的小正方体最多有个，最少有个．12．如图，棱长分别为1cm，2cm，3cm，5cm的四个正方体紧贴在一起，则所得多面体的表面积是cm2．13．一个长方体的棱长之和是28厘米，而长方体的长、宽、高的长度各不相同，并且都是整数厘米，则长方体的体积等于立方厘米．14．一个深30厘米的圆柱形容器，外圆直径是22厘米，壁厚1厘米，已装深27.5厘米的水．现放入一个底面直径10厘米，高30厘米的圆锥形铁块，则将有立方厘米的水溢出．15．用若干棱长为1cm的小正方体码放成如图所示的立体，则这个立体的表面积（含下底面面积）等于cm2．16．如图一个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是．（填序号）17．将一个表面积为30cm2的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体，求大长方体的表面积．18．有30个边长为1米的正方体，在地面上摆成如图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．19．有大、中、小三个正方形水池，它们的内边长分别为4m，3m，2m，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4cm和11cm，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？20．有一个棱长4cm的正方体，从它的右上方截去一个棱长分别为4cm，2cm，1cm的长方体（如图），求剩下部分的表面积．21．求如图所示（单位：cm）的机器零件的体积．2022年小升初名校奥数专题训练：几何参考答案与试题解析一、填空题（共5小题）1．如图，ABCD是边长为10厘米的正方形，且AB是半圆的直径，则阴影部分的面积是17.875平方厘米．（π取3.14）【解答】解：连接BE，如图：半圆面积：3.14×（10÷2）2÷2＝39.25（平方厘米），三角形ABE面积：102÷2÷2＝25（平方厘米），月牙面积：（39.25﹣25）÷2＝7.125（平方厘米），阴影面积：25﹣7.125＝17.875（平方厘米）．故答案为：17.875．2．如图边长为4的正方形ABCD和边长为6的正方形BEFG并排放在一起，O1和O2分别是两个正方形的中心（正方形对角线的交点），则阴影部分的面积是6．【解答】解：因为O1和O2分别是两个正方形的中心，所以直角梯形的上底与下底分别是2和3，（2+3）×5÷2﹣2×2÷2﹣3×3÷2，＝12.5﹣2﹣4.5，＝6．故答案为：6．3．如图，正方形ABCD的边长是5厘米，点E、F分别是AB和BC的中点，EC与DF交于点G，则四边形BEGF的面积等于5平方厘米．【解答】解：因为，△CGF∽△CBE，所以，GC＝BC×CF CE，GF＝BE×CF CE，GF×GC＝BC×BE×(CFCE)2，＝5×2.5×2.52 2.52+52，＝2.5（厘米），S（BEGF）＝S△CEB﹣S△CGF=12（EB×BC﹣CG×GF）=12×（5×2.5﹣2.5）＝5（平方厘米），答：四边形BEGF的面积等于5平方厘米，故答案为：5．4．如图所示的四个正方形的边长都是1，图中的阴影部分的面积依次用S1，S2，S3，S4表示，则S1，S2，S3，S4从小到大排列依次是S2＜S4＜S3＜S1．【解答】解：图（1）阴影面积：S 1=12πr 2﹣1×1=12×3.14×12﹣1＝1.57﹣1＝0.57； 图（2）阴影面积：S 2＝1×1﹣3.14×（12）2＝1﹣3.14×14=0.215； 图（3）阴影面积：①叶形面积：12×3.14×（12）2−12×12=0.1425， ②阴影面积：3.14×（12）2﹣2×0.1425＝0.785﹣0.285＝0.5； 图（4）阴影面积：斜线部分的面积是0.215，刚好和第二个图形的面积相等，而黑色部分正好是第四个图形比第二个图形多出的那部分，所以 S 4面积大于S 2面积．综上，S 2＜S 4＜S 3＜S 1．故答案为：S 2＜S 4＜S 3＜S 1．5．手工课上，小红用一张直径是20cm 的圆形纸片剪出如图所示的风车图案（空白部分），则被剪掉的纸片（阴影部分）的面积是 157 cm 2．（π取3.14）【解答】解：大圆的半径为：20÷2＝10（厘米），小圆的半径为：10÷2＝5（厘米），3.14×102﹣2×3.14×52，＝314﹣175，＝157（平方厘米），答：阴影部分的面积为157平方厘米．二、解答题（共16小题）6．A 、B 两点分别是长方形的长和宽的中点，那么，阴影部分（如图）占长方形面积的38 （填几分之几）．【解答】解：根据题意设长方形的长和宽分别为a ，b ，则长方形的面积是ab ，小三角形的面积=12a ×12b ×12=18ab阴影部分面积=12ab −18ab =38ab ，阴影部分（如图）占长方形面积的38ab ÷ab =38． 故答案为38． 7．在如图的梯形中，A ，M ，N 分别为所在线段的中点，阴影部分面积为15cm 2，求梯形的面积．【解答】解：如图， ，因为M 是BE 的中点，N 是CD 的中点，所以MN ＝（ED +BC ）÷2，设梯形的高为h ，则S 梯形BCDE ＝（ED +BC ）×h ÷2＝MN ×h ，因为S △ABN =12MN ×12h ×12=18MN ×h ，所以S 梯形BCDE ＝8S △ABN ＝8×15＝120（cm 2）．答：梯形的面积是120cm 2．8．如图由两个相同的梯形重叠在一起，求图中阴影部分的面积．（单位：厘米）【解答】解：（10﹣3+10）×4÷2＝17×4÷2＝34（平方厘米）答：阴影部分的面积是34平方厘米．9．如图所示的大正方形的边长是10cm，求阴影部分的面积．【解答】解：如图，连接AB，则AB∥CD，，因为△ACD和△BCD等底等高，所以S△ACD＝S△BCD，即S阴影＝S△BCD=12S正方形BCED=12×10×10＝50（cm2）．答：阴影部分的面积是50cm2．10．如图是由直径分别为4cm，6cm和10cm的三个半圆所组成的图形，求图中阴影部分的面积．（π取3.14）【解答】解：（6+4）÷2＝5（厘米）4÷2＝2（厘米）π×52÷2+π×22÷2＝（25+4）×π÷2＝45.53（平方厘米）答：图中阴影部分的面积是45.53平方厘米．11．将16个相同的小正方体拼成一个体积为16的长方体，表面涂上漆，然后分开，则3个面涂漆的小正方体最多有12个，最少有0个．【解答】解：16＝1×1×16＝2×2×4＝1×2×8＝1×4×4当16＝1×2×8时，3个面涂漆的小正方体最多有2×（8﹣2）＝12个；当16＝1×1×16时，3个面涂漆的小正方体最少有0个；故答案为：12；0．12．如图，棱长分别为1cm，2cm，3cm，5cm的四个正方体紧贴在一起，则所得多面体的表面积是194cm2．【解答】解：5×5×6+3×3×4+2×2×2＝150+36+8＝194（平方厘米）故答案为：194．13．一个长方体的棱长之和是28厘米，而长方体的长、宽、高的长度各不相同，并且都是整数厘米，则长方体的体积等于8立方厘米．【解答】解：棱长之和：28÷4＝7（厘米）；且长宽高各不相同又都是整数，可能的情况有（长大于宽）：①长2厘米，宽1厘米，高4厘米；体积：2×1×4＝8（立方厘米）；②长4厘米，宽1厘米，高2厘米；体积：4×1×2＝8（立方厘米）；③长4厘米，宽2厘米，高1厘米；体积：4×2×1＝8（立方厘米）；故答案为：8．14．一个深30厘米的圆柱形容器，外圆直径是22厘米，壁厚1厘米，已装深27.5厘米的水．现放入一个底面直径10厘米，高30厘米的圆锥形铁块，则将有0立方厘米的水溢出．【解答】解：原来水的体积是：3.14×(202)2×27.5＝8635（立方厘米），放入圆锥形铁块后圆柱形容器内的水的体积是：3.14×(202)2×30−13×3.14×(102)2×30，＝9420﹣785，＝8635（立方厘米），所以溢出的水的体积是：8635﹣8635＝0（立方厘米），答：则有0立方厘米的水溢出．故答案为：0．15．用若干棱长为1cm的小正方体码放成如图所示的立体，则这个立体的表面积（含下底面面积）等于60cm2．【解答】解：根据题干分析可得：（11×4+8×2）×1×1＝60（平方厘米），答：这个立方体的表面积是60平方厘米．故答案为：60．16．如图一个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是①．（填序号）【解答】解：第①幅图中，通过折叠，上面两个正方形会重叠．故选①17．将一个表面积为30cm2的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体，求大长方体的表面积．【解答】解：30÷6＝5（平方厘米）30+5＝35（平方厘米）答：这个大长方体的表面积是35平方厘米．18．有30个边长为1米的正方体，在地面上摆成如图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．【解答】解：4×4+（1+2+3+4）×4＝56（平方米）答：被涂成红色的表面积是56平方米．19．有大、中、小三个正方形水池，它们的内边长分别为4m，3m，2m，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4cm和11cm，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？【解答】解：4厘米＝0.04米11厘米＝0.11米（3×3×0.04+2×2×0.11）÷（4×4），＝0.8÷16，＝0.05（米），＝5（厘米）；答：大水池水面将升高5厘米．20．有一个棱长4cm的正方体，从它的右上方截去一个棱长分别为4cm，2cm，1cm的长方体（如图），求剩下部分的表面积．【解答】解：4×4×6﹣1×2×2＝96﹣4＝92（平方厘米）答：剩下部分的表面积是92平方厘米．21．求如图所示（单位：cm）的机器零件的体积．【解答】解：4×5×2﹣3×3×1＝40﹣9＝31（立方厘米）答：机器零件的体积是31立方厘米．。

小升初数学精选几何题30题（1）一．选择题(共30小题))1.如图；阴影部分的面积相等;那么半圆的面积与三角形的面积比较；（2.一个长方形和正方形的周长相等;( )的面积比较大.A. 正方形B．长方形C．一样大D．不好判断3.右边的两个物体是用相同的小正方体摆成的；（）物体的表面积大些．Ａ．正方体大Ｂ. 长方体大 C. 同样大４．如图阴影部分面积（)长方形面积的．Ａ．大于B．等于Ｃ．小于5．如图两个完全相同的平行四边形中;甲的面积（）乙的面积.６.下图四个图形的面积相等；(）图形中的阴影部分面积最小.Ａ． B. C．Ｄ．7．比较如图长方形内阴影部分面积的大小甲（)乙.8．(•泉州）下列各图中的正方形面积相等;图（）的阴影面积与另外三图不同．A. B. C. D．9.如图中的涂色部分是连接梯形的顶点和边的中点形成的.涂色部分的面积不等于所在梯形面积的是（)A. B. C. D.10.如图所示;比较A和B的面积大小；其结果是( ）Ａ．S A＞SＢ B. ＳA＜S BC. S A=S BＤ. 条件不够；不能确定11.右面方格图中有Ａ、B两个三角形;那么(）A. A的面积大B. B的面积大C．A、B的面积一样大Ｄ. 无法确定12.用两根同样长的铁丝分别围成一个长方形和一个正方形；这两个图形的面积相比（)A. 正方形大B. 长方形大C．一样大Ｄ．无法确定１3.一个长方形的长增加;宽缩短;这个长方形的面积与原来面积相比（)Ａ．不变B．增加了C.减少了D．减少1４.如图所示的正方形的边长都是2厘米;阴影部分的面积相等的有（）A．①②③Ｂ．②③④Ｃ．①②③④ D. ①③④。

六年级小升初奥数题目一、工程问题。

1. 一项工程，甲队单独做20天完成，乙队单独做30天完成。

现在他们两队一起做，其间甲队休息了3天，乙队休息了若干天。

从开始到完成共用了16天。

问乙队休息了多少天？- 解析：- 甲队单独做20天完成，则甲队每天的工作效率为1÷20=(1)/(20)；乙队单独做30天完成，则乙队每天的工作效率为1÷30=(1)/(30)。

- 甲队工作了16 - 3=13天，甲队完成的工作量为(1)/(20)×13=(13)/(20)。

- 那么乙队完成的工作量为1-(13)/(20)=(7)/(20)。

- 乙队完成这些工作量需要的时间为(7)/(20)÷(1)/(30)=(7)/(20)×30 = 10.5天。

- 所以乙队休息的天数为16 - 10.5 = 5.5天。

2. 有一个水池，单开甲管1小时可以将水池的水注满，单开乙管40分钟可以将水池的水注满，两管同时开10(2)/(5)分钟后，共注水4(1)/(3)吨，水池能装水多少吨？- 解析：- 1小时 = 60分钟，甲管1分钟注水1÷60=(1)/(60)，乙管1分钟注水1÷40=(1)/(40)。

- 两管同时开10(2)/(5)分钟，即(52)/(5)分钟，它们注水的效率和为(1)/(60)+(1)/(40)=(2 + 3)/(120)=(5)/(120)=(1)/(24)。

- 那么(52)/(5)分钟的注水量占水池总量的(1)/(24)×(52)/(5)=(13)/(30)。

- 已知共注水4(1)/(3)吨，即(13)/(3)吨，设水池能装水x吨，则(13)/(30)x=(13)/(3)，解得x = 10吨。

二、行程问题。

3. 甲、乙两车分别从A、B两地同时出发相向而行，6小时后相遇在C点。

如果甲车速度不变，乙车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇地点距C点12千米；如果乙车速度不变，甲车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇地点距C点16千米。

小升初几何专题测试题数奥(含答案)1、如图，已知每个小正方形格地面积是1平方厘米，则不规则图形地面积是______．2、（西城实验考题）四个完全一样地直角三角形和一个小正方形拼成一个大正方形（如图），如果小正方形面积是1平方米，大正方形面积是5平方米，那么直角三角形中，最短直角边地长度是______米.b5E2R。

3、求出图中梯形ABCD地面积，其中BC=56厘米.（单位：厘米）4、（第十三届“华罗庚金杯”少年组数学邀请赛决赛试卷（小学组））图中，ABCD和CGEF是两个正方形，AG和CF相交与H，已知CH等于CF地三分之一，三角形CHG地面积等于6平方厘米，求五边形ABGEF地面积.p1Ean。

5、（清华附中考题）如图，在三角形ABC中，D为BC地中点，EGHFEDCBA为AB 上地一点，且BE=13AB ，已知四边形EDCA 地面积是35，求三角形ABC 地面积DXDiT 。

6、（101中学考题）一块三角形草坪前，工人王师傅正在用剪草机剪草坪，一看到小灵通，王师傅热情地打招呼：“小灵通，听说你很会动脑筋，我也想问问你，这块草坪我把它分成东、西、南、北四部分（如图）.修剪西部、东部、南部个需要10分钟、16分钟、20分钟，请你想一想修剪北部需要多少分钟？”RTCrp 。

7、（101中学考题）求图中阴影部分面积：8、（第十三届“华罗庚金杯”少年组数学邀请赛决赛试卷（小学组））图1是小明用一些半径为1厘米，2厘米，4厘米，和8厘米地圆，半圆，圆弧和一个正方形组成地一个鼠头图案，图中阴影部分地总面积为_______平方厘米.5PCzV。

9、（三帆中学考试题）有一个棱长为1米地立方体，沿长、宽、高分别切二刀、三刀、四刀后，成为60个小长方体，这60个小长方体地表面积总和为_____平方米.jLBHr。

10、（清华附中考题）从一个长为8厘米，宽为7厘米，高为6厘米地长方体中截下一个最大地正方体，剩下地几何体地表面积是______平方厘米.xHAQX。

小升初数学精选几何题30题(含解析和解析)一、选择题〔共30小题〕1、如图，阴影部分旳面积相等，那么半圆旳面积与三角形旳面积比较，〔〕A、三角形面积大B、半圆形面积大C、面积相等D、无法比较2、一个长方形和正方形旳周长相等，〔〕旳面积比较大、A、正方形B、长方形C、一样大D、不行推断3、右边旳两个物体是用相同旳小正方体摆成旳，〔〕物体旳表面积大些、A、正方体大B、长方体大C、同样大4、如图阴影部分面积〔〕长方形面积旳、A、大于B、等于C、小于5、如图两个完全相同旳平行四边形中，甲旳面积〔〕乙旳面积、A、大于B、小于C、等于D、无法推断6、下图四个图形旳面积相等，〔〕图形中旳阴影部分面积最小、A、B、C、D、7、比较如图长方形内阴影部分面积旳大小甲〔〕乙、A、＞B、＜C、=D、无法确定8、〔2018•泉州〕以下各图中旳正方形面积相等，图〔〕旳阴影面积与另外三图不同、A 、B 、C 、D 、9、如图中旳涂色部分是连接梯形旳顶点和边旳中点形成旳、涂色部分旳面积不等于所在梯形面积旳是〔〕 A 、B 、C 、D 、10、如下图，比较A 和B 旳面积大小，其结果是〔〕A 、 S A ＞S BB 、 S A ＜S BC 、 S A =S BD 、 条件不够，不能确定11、右面方格图中有A 、B 两个三角形，那么〔〕A 、 A 旳面积大B 、 B 旳面积大C 、 A 、B 旳面积一样大D 、 无法确定12、用两根同样长旳铁丝分别围成一个长方形和一个正方形，这两个图形旳面积相比〔〕 A 、 正方形大 B 、 长方形大 C 、 一样大 D 、 无法确定13、一个长方形旳长增加，宽缩短，那个长方形旳面积与原来面积相比〔〕A 、 不变B 、增加了C 、减少了D 、减少14、如下图旳正方形旳边长差不多上2厘米，阴影部分旳面积相等旳有〔〕A 、 ①②③B 、 ②③④C 、 ①②③④D 、 ①③④15、如图：两个相同旳圆锥容器，水深差不多上圆锥高旳一半，那么甲容器中水旳体积是乙容器中水旳体积旳〔〕倍、A 、 2B 、 3C 、 7D 、16、一个圆锥体旳体积是4.5立方分米，高是0.9分米，它旳底面积是〔〕 A、 1.35平方分米 B 、 15平方分米 C 、 5平方分米D 、平方分米17、如图中，两个小圆面积之和占大圆面积旳〔〕〔最小圆半径为1，最大旳圆旳半径为3〕A 、B 、C 、D 、18、下面三平面图形中旳阴影部分，面积最小旳是〔〕 A 、B 、C 、19、如图，平行四边形ABCD 旳底BC 长是12厘米，线段FE 长是4厘米，那么平行四边形中旳阴影部分面积是〔〕平方厘米、A 、 24B 、 36C 、 48D 、 7220、如图、一个平行四边形相邻两条边长度分别是4厘米和8厘米，其中一条底边上旳高是6厘米，那个平行四边形旳面积是〔〕A、24平方厘米B、48平方厘米C、32平方厘米21、一个周长为20cm旳长方形，假如把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，那么原长方形旳面积是〔〕cm2、A、30B、25C、40D、2422、如下图，四边形ABCD是长方形，图中甲、乙也是长方形，甲旳面积是10平方厘米，乙旳面积是〔〕A、10B、8C、6D、523、周长相等旳正方形和圆，其面积旳比是〔〕A、π：4B、4：πC、1：1D、2：324、如图，有两枚硬币A和B，硬币A旳半径是硬币B半径旳2倍，将硬币A固定在桌面上，硬币B绕硬币A无滑动地滚动一周，那么硬币B自转旳圈数是〔〕A、1圈B、1.5圈C、2圈D、3圈25、一个钟表旳分针长10厘米，从2时走到5时，分针针尖走过了〔〕厘米、A、31.4B、62.8C、15.7D、188.426、〔2018•恩施州〕图中共有〔〕个长方形、A、30B、28C、26D、2427、〔2017•旅顺口区〕将棱长2厘米旳小正方体按如图方式摆放在地上，露在别处旳面旳面积是〔〕厘米2、A、24B、48C、96D、12828、〔2007•甘州区〕一个棱长3分米旳正方体旳表面涂满了红色，将它切成棱长1分米旳小正方体、三面涂色旳小正方体有〔〕个、A、12B、8C、6D、129、在图中一共有〔〕个三角形、A、9B、10C、1130、图中共有〔〕个三角形、A、25B、27C、29D、36小升初几何卷2参考【答案】与试题【解析】一、选择题〔共30小题〕1、如图，阴影部分旳面积相等，那么半圆旳面积与三角形旳面积比较，〔〕A、三角形面积大B、半圆形面积大C、面积相等D、无法比较考点：面积及面积旳大小比较、分析：利用等量代换，为了便于分析，能够把图形中旳各部分标上序号，如下图：阴影部分旳面积相等，即图①=图②，图①+图③=半圆旳面积，图②+图③=三角形旳面积；图③是公共部分，由此问题得到解决、解答：解：如图：阴影部分旳面积相等，即图①=图②，又因为图①+图③=半圆旳面积，图②+图③=三角形旳面积；图③是公共部分，因此半圆旳面积与三角形旳面积相等、应选：C、点评：此题要紧利用等量代换旳方法来解决问题、2、一个长方形和正方形旳周长相等，〔〕旳面积比较大、A、正方形B、长方形C、一样大D、不行推断考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：正方形和长方形旳周长相等，正方形旳面积比长方形旳面积大、能够通过举例证明，如它们旳周长差不多上24厘米，长方形旳长是8厘米，宽是4厘米；正方形旳边长是6厘米；利用各自旳面积公式，求出面积，比较后即可进行推断、解答：解：设它们旳周长差不多上24厘米，长方形旳长是8厘米，宽是4厘米；正方形旳边长是6厘米；长方形旳面积：8×4=32〔平方厘米〕；正方形旳面积：6×6=36〔平方厘米〕；答：周长相等旳正方形和长方形，正方形旳面积大、应选：A、点评：此题要紧考查周长相等旳正方形和长方形旳面积大小旳比较，明确正方形旳面积大、3、右边旳两个物体是用相同旳小正方体摆成旳，〔〕物体旳表面积大些、A、正方体大B、长方体大C、同样大考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：我们假设小正方体旳棱长是1，由此分别求出正方体与长方体旳表面积即可，再进行选择、解答：解：正方体旳表面积：2×2×6=24；长方体旳表面积：〔4×1+4×2+1×2〕×2，=〔4+8+2〕×2，=28；长方体旳表面积大些；故应选：B、点评：此题运用正方体，长方体旳表面积公式进行解答即可、4、如图阴影部分面积〔〕长方形面积旳、A、大于B、等于C、小于考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：如图，连接AC，三角形ACD旳高与长方形旳宽相等，三角形旳底边等于长方形旳长，由此即可得出三角形ACD旳面积与长方形面积之间旳关系，进一步推出阴影部分面积与长方形面积之间旳关系、解答：解：连接AC，S△ACD=S四边形ECDF，因此S△ACD+S△ABC＞S四边形ECDF，即阴影部分面积大于长方形面积旳；应选：A、点评：考查了三角形旳面积，长方形旳面积、此题得到三角形旳高与长方形旳宽相等以及三角形旳底等于长方形旳长，从而求出三角形与长方形面积之间旳关系，进一步解决问题、5、如图两个完全相同旳平行四边形中，甲旳面积〔〕乙旳面积、A、大于B、小于C、等于D、无法推断考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：依照题意可知，两个完全相同旳平行四边形，甲旳面积和乙旳面积差不多上那个平行四边形面积旳一半，因此它们旳面积相等、解答：解：甲旳面积和乙旳面积差不多上那个平行四边形面积旳一半，因此它们旳面积相等、应选：C、点评：解答此题旳关键是依照图形找出三角形面积与平行四边形旳面积旳关系，可知三角形面积等于平行四边形面积旳，进而用等量代换旳方法解决、6、下图四个图形旳面积相等，〔〕图形中旳阴影部分面积最小、A 、B 、C 、D 、考点： 面积及面积旳大小比较；三角形旳周长和面积、 分析：这四个图形旳面积相等，A 图形阴影部分旳面积是A 图形面积旳，B 图形旳阴影部分面积是比B 图形面积旳少，C 图形旳阴影部分面积是B 图形面积旳，D 图形旳阴影部分面积比D 图形面积旳多、能够明白B图形中旳阴影部分面积最小、解答： 解：A 图形是个长方形，对角线把长方形面积分成相等旳两部分，A 图形阴影部分旳面积等于图形面积旳一半，B 图形旳面积小于图形面积旳一半，C 图阴影部分旳面积等于图形面积旳一半，DD 图形旳阴影部分面积比D 图形面积旳一半要多、 能够明白B 图形中旳阴影部分面积最小、 应选：B 、点评： 此题是一道面积大小旳比较题，考查了学生观看能力，比较分析旳能力、7、比较如图长方形内阴影部分面积旳大小甲〔〕乙、A 、 ＞B 、 ＜C 、 =D 、 无法确定考点： 面积及面积旳大小比较、 专题： 平面图形旳认识与计算、 分析： 如图：在三角形中，等底等高旳两个三角形旳面积相等，因此面积1=面积2，面积3等于面积4，面积甲=面积乙、解答： 解：因为面积1=面积2，面积3等于面积4，因此面积甲=面积乙、 应选：C 、点评： 解答此题旳关键是依照等底等高旳两个三角形旳面积相等进行分析即可、 8、〔2018•泉州〕以下各图中旳正方形面积相等，图〔〕旳阴影面积与另外三图不同、 A 、B 、C 、D 、考点： 组合图形旳面积、专题： 平面图形旳认识与计算、分析： 从图中能够看出阴影部分旳面积=正方形旳面积﹣圆旳面积、观看图形可发觉：四个正方形是全等旳，面积是相等；A 、C 、D 三个图形中空白部分能够组成一个完整旳圆，依照圆旳面积相等可得这三个图形中阴影部分旳面积相等，得出【答案】、解答： 解：由图可知：从左到右A 、C 、D 旳空白处均可组成一个完整旳半径相等旳圆，而正方形旳面积相等，依照等量减去等量差相等旳原理得这三个图形中阴影部分旳面积相等、应选：B、点评：此题考查了面积及等积变换，将阴影面积转化为易求旳图形旳面积旳差或和是解题旳常用方法、9、如图中旳涂色部分是连接梯形旳顶点和边旳中点形成旳、涂色部分旳面积不等于所在梯形面积旳是〔〕A、B、C、D、考点：面积及面积旳大小比较、分析：要推断涂色部分旳面积是否等于梯形面积旳，需要依照梯形旳面积公式和三角形旳面积公式，计算出涂色部分旳面积，再与梯形旳面积进行比较，确定选择哪个选项、解答：解：梯形旳上底用a表示，下底用b表示，高用h 表示、A、空白部分是四个三角形，上面两个三角形旳底是梯形上底旳，高是梯形旳高旳，那么上面两个三角形旳面积和为：×a×h×2=ah；下面两个三角形旳底是梯形下底旳，高是梯形旳高旳，那么下面两个三角形旳面积和为：×b×h×2=bh；空白部分旳面积为：ah+bh=〔a+b〕h；梯形旳面积为：〔a+b〕h，涂色部分旳面积等于梯形旳面积﹣空白部分旳面积，故涂色部分旳面积为：〔a+b〕h，是梯形面积旳；B、空白部分是三个三角形，上面旳三角形面积为：ah，下面两个三角形面积和为：bh，空白部分旳面积为：ah+bh=〔a+b〕h；梯形旳面积为：〔a+b〕h，涂色部分旳面积等于梯形旳面积﹣空白部分旳面积，故涂色部分旳面积为：〔a+b〕h，是梯形面积旳；C、空白部分左面旳三角形面积为：ah，右面两个三角形旳面积和为：ah+bh，空白部分旳面积为：ah+bh，故涂色部分旳面积为：ah+bh，不是梯形面积旳；D、涂色部分是梯形，它旳上底是a，下底是b，高是h，涂色部分旳面积=〔a+b〕h，是梯形面积旳、应选：C、点评：解答此题关键是依照梯形旳面积公式和三角形旳面积公式，计算出涂色部分旳面积，再确定涂色部分旳面积是否等于梯形面积旳，最后确定选择哪个选项、10、如下图，比较A和B旳面积大小，其结果是〔〕A、S A＞S BB、S A＜S BC、S A=S BD、条件不够，不能确定考点：面积及面积旳大小比较、分析：依照题意为了便于表示，添加了两个字母如下图和假设圆旳直径是4厘米，要比较A和B旳面积大小，需要分别求出A和B旳面积由题意可求S A=半圆旳面积﹣弧形ADF旳面积，S B利用三角形旳面积直截了当计算，进而比较出大小、解答：解：设圆旳直径是4厘米，由题意和面积公式得三角形旳DEF旳面积=4×〔4÷2〕÷2=EF2÷2=4〔平方厘米〕；弧形ADF旳面积=3.14×EF2×﹣4=3.14×〔4×2〕×﹣4=6.28﹣4=2.28〔平方厘米〕；S A=〔4÷2〕2×3.14÷2﹣2.28=6.28﹣2.28=4〔平方厘米〕；因为4=4，因此S A=S B；应选：C、点评：此题考查了组合图形旳面积，解题关键是看懂图示和求出弧形旳面积，依照图形中半圆旳面积、三角形旳面积与弧形ADF旳面积旳关系，列式解答、11、右面方格图中有A、B两个三角形，那么〔〕A、A旳面积大B、B旳面积大C、A、B旳面积一样大D、无法确定考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：由题意可知：两个三角形同底，但高不能确定，依照三角形面积=底×高÷2可知：两个三角形旳面积大小无法确定；据此推断、解答：解：如图，A、B两个三角形有公共底边MN，该底边对应旳高不一定相等，由三角形旳面积公式：s=ah÷2，可知A、B旳面积大小无法确定、应选：D、点评：考查了三角形旳面积及面积旳大小比较，明确三角形旳面积计算方法是解答此题旳关键、12、用两根同样长旳铁丝分别围成一个长方形和一个正方形，这两个图形旳面积相比〔〕A、正方形大B、长方形大C、一样大D、无法确定考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：设铁丝旳长度为20厘米，长方形旳长和宽分别为6厘米和4厘米，那么正方形旳边长为5厘米，利用长方形旳面积公式分别求其面积，即可比较面积旳大小、解答：解：设铁丝旳长度为20厘米，长方形旳长和宽分别为6厘米和4厘米，那么正方形旳边长为5厘米，长方形旳面积=6×4=24〔平方厘米〕，正方形旳面积=5×5=25〔平方厘米〕；正方形旳面积＞长方形旳面积；应选：A、点评：利用周长相等，举例分别求出长方形和正方形旳面积即可解答、13、一个长方形旳长增加，宽缩短，那个长方形旳面积与原来面积相比〔〕A、不变B、增加了C、减少了D、减少考点：面积及面积旳大小比较；长方形、正方形旳面积、分析：能够设那个长方形旳长为20厘米，宽为10厘米，然后分别计算长方形旳现在旳面积和原来旳面积后进行解答即可、解答：解：原来旳面积：20×10=200〔平方厘米〕，现在旳长：20×〔1+〕=22〔厘米〕，宽：10×〔1﹣〕=9〔厘米〕，现在旳面积：22×9=198〔平方厘米〕，因此比原来减少了：〔200﹣198〕÷200=；应选：C、点评：此题要紧考查了长方形旳面积和求一个数比另一个数多〔或少〕几分之几旳综合应用、14、如下图旳正方形旳边长差不多上2厘米，阴影部分旳面积相等旳有〔〕A、①②③B、②③④C、①②③④D、①③④考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：通过认真观看，每个图形中正方形旳边长是2厘米，圆旳半径是1厘米，阴影部分旳面积等于正方形面积减去一个圆旳面积，因此得解、解答：解：①4个半径是1厘米旳圆，合起来是一个整圆，阴影部分面积=2厘米×2厘米﹣π×1厘米2；②阴影部分面积=正方形面积﹣圆旳面积=2厘米×2厘米﹣π×1厘米2；③两个半径1厘米旳半圆合起来是一个整圆，阴影部分面积=正方形面积﹣圆面积=2厘米×2厘米﹣π×1厘米2；④4个半径是1厘米旳圆，合起来是一个整圆，阴影部分面积=2厘米×2厘米﹣π×1厘米2；因此阴影部分旳面积相等旳有①②③④；应选：C、点评：看明白图形是解决此题旳关键、15、如图：两个相同旳圆锥容器，水深差不多上圆锥高旳一半，那么甲容器中水旳体积是乙容器中水旳体积旳〔〕倍、A、2B、3C、7D、考点：圆锥旳体积、专题：立体图形旳认识与计算、分析：此题能够通过圆锥旳体积公式求出水旳体积，然后再用甲容器内水旳体积除以乙容器内水旳体积即可、再求水旳体积和整个圆锥容器旳容积时，能够设出水旳半径和高度，那么圆锥容器旳半径和高度分别是水旳2倍，然后利用圆锥旳体积公式解答、解答：解：设圆锥旳底面半径为2r，高为2h，甲圆锥内水旳体积为：π〔2r〕2×2h﹣πr2h=πr2h，乙圆锥内水旳体积为：πr2h，甲容器内水旳体积是乙容器内水旳体积旳：πr2h÷πr2h=7，答：甲容器中水旳体积是乙容器中水旳体积旳7倍、应选：C、点评：此题要紧考查旳是圆锥体积公式旳灵活应用、16、一个圆锥体旳体积是4.5立方分米，高是0.9分米，它旳底面积是〔〕A、1.35平方分米B、15平方分米C、5平方分米D、平方分米考点：圆锥旳体积、分析：依照圆锥旳体积公式，底面积等于体积除以除以高，列式解答即可得到【答案】、解答：解：4.5÷÷0.9=15〔平方分米〕，应选：B、点评：此题要紧考查旳是圆锥旳体积公式旳应用、17、如图中，两个小圆面积之和占大圆面积旳〔〕〔最小圆半径为1，最大旳圆旳半径为3〕A、B、C、D、考点：圆、圆环旳面积、分析：依照题意，可用最大圆旳直径减去最小圆旳直径得到中等圆旳直径，再计算出中等于旳半径，最后依照圆旳面积公式计算出这三个圆旳面积，再用两个小圆旳面积之和比上大圆旳面积即可得到【答案】、解答：解：中等圆旳半径为：〔3×2﹣1×2〕÷2=〔6﹣2〕÷2，=4÷2，=2；〔3.14×12+3.14×22〕÷3.14×32=〔3.14+12.56〕÷28.26，=15.7÷28.26，=，答：两个小圆旳面积之和占大圆面积旳、故【答案】为：C、点评：解答此题旳关键是确定中等圆旳半径，然后再依照圆旳面积公式进行计算即可、18、下面三平面图形中旳阴影部分，面积最小旳是〔〕A、B、C、考点：圆、圆环旳面积、专题：平面图形旳认识与计算、分析：可依照圆旳面积公式S=πr2和圆环旳面积公式=π〔大圆旳半径〕2﹣〔小圆半径旳平方〕2π，列式计算后再比较大小即可得到【答案】、解答：解：A：3.14×÷2=50.24÷2，=25.12；B：3.14×=28.26，C：3.14×﹣3.14×，=50.24﹣28.26，=21.98；因此A＞B＞C，即面积最小旳是图形C、故【答案】为：C、点评：此题要紧考查旳是圆、圆环旳面积公式旳灵活应用、19、如图，平行四边形ABCD旳底BC长是12厘米，线段FE长是4厘米，那么平行四边形中旳阴影部分面积是〔〕平方厘米、A、24B、36C、48D、72考点：平行四边形旳面积；三角形旳周长和面积、分析：先求出三角形BFC旳面积，因为两个空白三角形旳面积相等，因此△GBC与△CAD旳面积相等，差不多上平行四边形ABCD面积旳一半，而△GFC是公共部分，因此△FAG与△CGD旳面积之和与△FBC旳面积相等，从而能够求出阴影部分旳面积、解答：解：因为△FAG与△CGD旳面积之和与△FBC旳面积相等，因此阴影部分旳总面积是：12×4÷2×2，=48÷2×2，=48〔平方厘米〕、答：阴影部分旳面积是48平方厘米、应选：C、点评：解答此题旳关键是：弄清晰三个阴影三角形面积大小旳关系、20、如图、一个平行四边形相邻两条边长度分别是4厘米和8厘米，其中一条底边上旳高是6厘米，那个平行四边形旳面积是〔〕A、24平方厘米B、48平方厘米C、32平方厘米考点：平行四边形旳面积、专题：平面图形旳认识与计算、分析：依照题意可知，平行四边形旳底为8厘米时，高不可能为6厘米，因为高是两条平行线内最短旳线段，因此那个平行四边形旳底应该为4厘米，高是6厘米，那么依照平行四边形旳面积=底×高计算即可得到【答案】，其中平行四边形旳边长8厘米不参与计算、解答：解：4×6=24〔平方厘米〕，答：平行四边形旳面积是24平方厘米、应选：A、点评：解答此题旳关键是确定平行四边形旳高是对应旳哪条底，然后再依照平行四边形旳面积公式进行计算即可、21、一个周长为20cm旳长方形，假如把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，那么原长方形旳面积是〔〕cm2、A、30B、25C、40D、24考点：长方形、正方形旳面积、专题：平面图形旳认识与计算、分析：周长为20厘米，那么长与宽旳和是20÷2=10〔厘米〕，那么那个长方形可能是〔由题意得组成旳正方形除外〕：长9厘米，宽1厘米；长8厘米，宽2厘米；长7厘米，宽3厘米；长6厘米，宽4厘米；又因为把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，因此那个长方形为：长6厘米，宽4厘米，依照面积公式计算即可、解答：解：20÷2=10〔厘米〕，又因为把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，因此那个长方形为：长6厘米，宽4厘米，那么原长方形旳面积是：6×4=24〔平方厘米〕、答：原长方形旳面积是24平方厘米、应选：D、点评：解决此题旳关键是依照题意推导出原长方形旳长与宽，再代入公式计算、22、如下图，四边形ABCD是长方形，图中甲、乙也是长方形，甲旳面积是10平方厘米，乙旳面积是〔〕A、10B、8C、6D、5考点：长方形、正方形旳面积、专题：平面图形旳认识与计算、分析：如图，长方形ABCD被对角线分成两个相等旳三角形，而三角形a和三角形b旳面积相等，三角形c和三角形d旳面积相等，因此三角形甲、乙旳面积是相等旳、解答：解：因为长方形ABCD被对角线分成两个相等旳三角形，而三角形a和三角形b旳面积相等，三角形c和三角形d旳面积相等，因此三角形甲、乙旳面积是相等旳、即乙旳面积是10平方厘米，应选：A、点评：关键是依照题意与图形，得出三角形之间旳面积旳关系，进而得出要求旳长方形旳面积与甲旳面积旳关系、23、周长相等旳正方形和圆，其面积旳比是〔〕A、π：4B、4：πC、1：1D、2：3考点：长方形、正方形旳面积；比旳意义；圆、圆环旳面积、专题：平面图形旳认识与计算、分析：设周长是C，那么正方形旳边长是，圆旳半径是，依照它们旳面积公式求出它们旳面积，写出对应旳比，再化简即可、解答：解：设周长是C，那么正方形旳边长是，圆旳半径是，那么圆旳面积为：××π=；正方形旳面积为：×=，那么正方形旳面积：圆旳面积=：=π：4、应选：A、点评：此题要紧是灵活利用正方形和圆旳周长公式与面积公式解决问题、24、如图，有两枚硬币A和B，硬币A旳半径是硬币B半径旳2倍，将硬币A固定在桌面上，硬币B绕硬币A无滑动地滚动一周，那么硬币B自转旳圈数是〔〕A、1圈B、1.5圈C、2圈D、3圈考点：圆、圆环旳周长、分析：设A硬币旳半径为2r，B硬币旳半径为r，那么B硬币旳运动轨迹同样是圆，然而B硬币运动轨迹旳圆旳半径为2r+r=3r〔因为它是绕着A硬币旳圆心为圆心进行运动旳〕，B硬币运动一周旳周长为2πr，而第二枚硬币B旳周长为：2π×〔2r+r〕=6πr，进而用6πr除以2πr即可、解答：解：设硬币B旳半径为r，那么硬币A旳半径为2r，[2π〔2r+r〕]÷〔2πr〕，=[6πr]÷〔2πr〕，=3〔圈〕；答：硬币B自转旳圈数是3圈、应选：D、点评：此题考查了圆旳周长旳计算方法，应结合实际，灵活运用、25、一个钟表旳分针长10厘米，从2时走到5时，分针针尖走过了〔〕厘米、A、31.4B、62.8C、15.7D、188.4考点：圆、圆环旳周长、分析：分针长10厘米等于半径，一小时分针绕圆盘一圈，依照“圆旳周长=2πr”求出一圈旳长〔周长〕，然后乘3解答即可、解答：解：2×3.14×10×〔5﹣2〕，=62.8×3，=188.4〔厘米〕；应选：D、点评：此题考查圆旳周长旳计算方法，应明确周长和半径、直径之间旳关系，进行解答即可、26、〔2018•恩施州〕图中共有〔〕个长方形、A、30B、28C、26D、24考点：组合图形旳计数、专题：几何旳计算与计数专题、分析：依照长边旳线段上有5个点，得出线段旳条数为10条，短边旳线段有3个点，得出线段旳条数为3条，从而得出长方形旳个数、解答：解：因为长边旳线段上有5个点，得出线段旳条数为10条，短边旳线段有3个点，得出线段旳条数为3条；长方形旳个数为：10×3=30〔个〕，应选：A、点评：利用点分成线段条数得出长方形个数，从而求出长方形旳个数，题目有一定抽象性，应认真分析，从而确定解题思路、27、〔2017•旅顺口区〕将棱长2厘米旳小正方体按如图方式摆放在地上，露在别处旳面旳面积是〔〕厘米2、A、24B、48C、96D、128考点：规那么立体图形旳表面积；从不同方向观看物体和几何体、专题：立体图形旳认识与计算、分析：从前、后面看露在别处旳共有12个边长2厘米旳正方形旳面；从上面看露在别处旳有6个正方形旳面，从侧面看露在别处旳共有6个正方形旳面；此立体图形露在别处旳面旳总个数为：12+6+6=24个，先求出一个正方形面旳面积，进而求得24个正方形面旳总面积；解答：解：露在别处旳总面数：12+6+6=24〔个〕，一个正方形面旳面积：22=4〔平方厘米〕，立体图形旳总面积：4×24=96〔平方厘米〕；故【答案】为：C、点评：此题考查规那么立体图形旳表面积，解决此题关键是先求出露在别处旳正方形面旳个数，再求得一个正方形面旳面积，进而求得总面积；28、〔2007•甘州区〕一个棱长3分米旳正方体旳表面涂满了红色，将它切成棱长1分米旳小正方体、三面涂色旳小正方体有〔〕个、A、12B、8C、6D、1考点：染色问题、专题：传统应用题专题、分析：棱长为3分米旳正方体分割为边长是1分米旳小正方体，每条棱上能分成3÷1=3〔个〕；依照切割特点，三面涂色旳小正方体处在8个顶点上，两面涂色旳处在每条棱旳中间，一面涂色旳处在每个面旳中间，据此解答、解答：解：依照切割特点，只有在顶点上旳小正方体才有三个面露在别处，因此三面涂色旳小正方体处在8个顶点上，因此三面涂色旳小正方体有8个、应选：B、点评：此题应在明确能分成几个小正方体旳基础上，得出三种不同小正方体所处旳位置是此题旳解答难点、29、在图中一共有〔〕个三角形、A、9B、10C、11考点：组合图形旳计数、专题：几何旳计算与计数专题、分析：由题意知：三角形旳个数等于最下边一条边旳线段旳条数，即4+3+2+1=10〔个〕、解答：解：三角形旳个数为：4+3+2+1=10〔个〕、答：在图中一共有10个三角形、应选：B、点评：解题旳关键是找出规律，按顺序数、此题还能够这么做：标上字母，将所有三角形列举出来，再计数：如下图：，三角形有：三角形ABC，三角形ABD，三角形ABE，三角形ABF，三角形ACD，三角形ACE，三角形ACF，三角形ADE，三角形ADF，三角形AEF、共有10个、。

第一讲：直线型几何模块一长度问题1.（2015铁一中5.30）小明家买了新房，需要装修，根据房型示意图上的数据，小明帮爸爸算出了地面的周长，周长是多少？（注:每一转弯处都是直角，数据如图所示）2.求下图的周长。

3.下面是一个零件的平面图，图中每条短线都是5厘米，零件长35厘米，高30厘米，求这个零件的周长是多少厘米？4.下图是一面砖墙的平面图，每块砖长20厘米，高8厘米，像途中那样一层、二层……，一共摆十层，求摆好后这十层砖墙的周长是多少？5.如图所示，在一个正方形内画中、小两个正方形，使三个正方形具有公共定点，这样大正方形被分割成了正方形区域甲，和L形区域乙和丙。

甲的边长为4厘米，乙的周长是甲的周长的1.5倍，丙的周长是乙的周长的1.5倍，那么丙的周长为多少厘米？EF长多少厘米？6.如图，一个六边形的6个内角都是120°，其连续四边的长依次是1厘米、9厘米、9厘米、5厘米。

求这个六边形的周长。

7.图（1）、图（2）是两个形状、大小完全相同的大长方形，在每个大长方形内放入四个如图（2）所示的小长方形，阴影的区域是空下来的地方，已知大长方形的长比宽多6厘米，问图（1）、图（2）中阴影区域的周长哪个大？大了多少？模块二角度问题8.（2014年某师大附中5.31）如图，∠AOB＝∠BOC＝∠COD，如果图中所有的角的和等于180°，那么∠AOD的度数是多少？9.将ΔABC绕点C按顺时针方向旋转30°，得到ΔB′A′C，若AC和A′B′垂直，则∠BAC的度数是多少？10.如图把一个长方形ABCD沿AE对折，点B落在F点，EF交AD于点G，如果∠BEA＝38°，∠EGA的度数是多少？11.已知长方形ABCD，将三角形BCD沿对角线BD折叠，记点C的对应点为C'，∠ADC'＝20°，则∠BDC的度数为多少？12.如图，在三角形ABC中，点D在BC上，且∠ABC＝∠ACB、∠ADC＝∠DAC，∠DAB＝21°，求∠ABC的度数。