2020年高考复习数学算法初步
- 格式:doc
- 大小:850.45 KB
- 文档页数:13

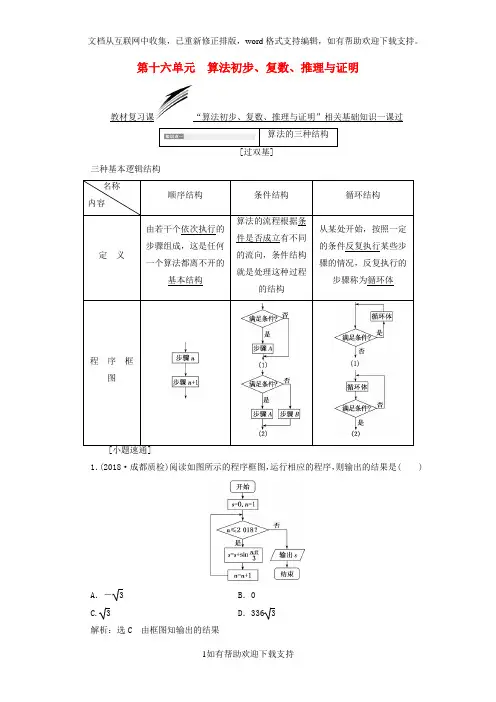
第十六单元算法初步、复数、推理与证明教材复习课“算法初步、复数、推理与证明”相关基础知识一课过算法的三种结构[过双基]三种基本逻辑结构名称内容顺序结构条件结构循环结构定义由若干个依次执行的步骤组成,这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向,条件结构就是处理这种过程的结构从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体程序框图1.(2018·成都质检)阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )A.- 3 B.0C. 3 D.336 3解析:选C 由框图知输出的结果s =sin π3+sin2π3+…+sin 2 018π3, 因为函数y =sin π3x 的周期是6,所以s =336⎝ ⎛⎭⎪⎫sin π3+sin 2π3+…+sin 6π3+sin π3+sin 2π3=336×0+32+32= 3.2.执行如图所示的程序框图.若输出y =-3,则输入的角θ=( )A.π6 B .-π6C.π3D .-π3解析:选D 由输出y =-3<0,排除A 、C ,又当θ=-π3时,输出y =-3,故选D.3.执行如图所示的程序框图,已知输出的s ∈[0,4],若输入的t ∈[m ,n ],则实数n -m 的最大值为( )A .1B .2C .3D .4解析:选D 由程序框图得s =⎩⎪⎨⎪⎧3t ,t <1,4t -t 2,t ≥1,作出s 的图象如图所示.若输入的t ∈[m ,n ],输出的s ∈[0,4],则由图象得n -m 的最大值为4.4.某程序框图如图所示,若输出的p 值为31,则判断框内应填入的条件是( )A .n >2?B .n >3?C .n >4?D .n >5?解析:选B 运行程序:p =1,n =0;n =1,p =2;n =2,p =6;n =3,p =15;n =4,p =31,根据题意,此时满足条件,输出p =31,即n =3时不满足条件,n =4时满足条件,故选B.[清易错]1.易混淆处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.2.易忽视循环结构中必有选择结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.某程序框图如图所示,若该程序运行后输出的值是74,则a =________.解析:由已知可得该程序的功能是计算并输出S =1+11×2+12×3+…+1aa +1=1+1-12+12-13+…+1a -1a +1=2-1a +1. 若该程序运行后输出的值是74,则2-1a +1=74, 解得a =3. 答案:3复数的基本运算 [过双基]1.复数的有关概念 名称 内容备注复数的概念 形如a +b i(a ∈R ,b ∈R)的数叫复数,其中实部为a ,虚部为b若b =0,则a +b i 为实数;若a =0且b ≠0,则a +b i 为纯虚数 复数相等 a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R)共轭复数a +b i 与c +d i 共轭⇔a =c 且b =-d (a ,b ,c ,d ∈R)复平面建立平面直角坐标系来表示复数的平面叫做复平面,x 轴叫实轴,y 轴叫虚轴 实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,各象限内的点都表示虚数复数的模设OZ ―→对应的复数为z =a +b i ,则向量OZ ―→的长度叫做复数z =a +b i 的模|z |=|a +b i|=a 2+b 22.复数的几何意义复数集C 和复平面内所有的点组成的集合是一一对应的,复数集C 与复平面内所有以原点O 为起点的向量组成的集合也是一一对应的,即(1)复数z =a +b i 一一对应复平面内的点Z (a ,b )(a ,b ∈R). (2)复数z =a +b i(a ,b ∈R)一一对应平面向量OZ ―→. 3.复数的运算设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R),则①加法:z 1+z 2=(a +b i)+(c +d i)=(a +c )+(b +d )i ; ②减法:z 1-z 2=(a +b i)-(c +d i)=(a -c )+(b -d )i ; ③乘法:z 1·z 2=(a +b i)·(c +d i)=(ac -bd )+(ad +bc )i ; ④除法:z 1z 2=a +b ic +d i =a +b ic -d ic +d i c -d i=ac +bd +bc -ad ic 2+d 2(c +d i≠0).[小题速通]1.(2016·全国卷Ⅲ)若z =4+3i ,则z|z |=( )A .1B .-1C.45+35iD.45-35i 解析:选D ∵z =4+3i ,∴z =4-3i ,|z |=42+32=5, ∴z|z |=4-3i 5=45-35i. 2.若复数z 满足(1+i)z =|3+i|,则在复平面内,z 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析:选A 由题意,得z =32+121+i =21-i1+i 1-i=1-i ,所以z =1+i ,其在复平面内对应的点为(1,1),位于第一象限.3.复数2i1+i (i 为虚数单位)实部与虚部的和为( )A .2B .1C .0D .-2解析:选A 因为2i1+i =2i 1-i 1+i 1-i =1+i ,所以复数2i1+i(i 为虚数单位)实部与虚部的和为2.4.已知(1+2i)z =4+3i ,则z =________. 解析:∵z =4+3i 1+2i =4+3i 1-2i 1+2i 1-2i =10-5i5=2-i ,∴z =2+i. 答案:2+i[清易错]1.利用复数相等a +b i =c +d i 列方程时,注意a ,b ,c ,d ∈R 的前提条件. 2.注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来.例如,若z 1,z 2∈C ,z 21+z 22=0,就不能推出z 1=z 2=0;z 2<0在复数范围内有可能成立.1.已知4+m i1+2i ∈R ,且m ∈R ,则|m +6i|=( )A .6B .8C .8 3D .10解析:选D4+m i 1+2i =4+m i1-2i 1+2i1-2i =4+2m +m -8i5,因为复数4+m i1+2i ∈R ,故m =8,所以|m +6i|=|8+6i|=10.2.已知5i2-i =a +b i(a ,b ∈R ,i 为虚数单位),则a +b =______.解析:5i 2-i =5i 2+i 2-i 2+i=-1+2i , 由5i2-i=a +b i ,得-1+2i =a +b i ,∴a =-1,b =2, ∴a +b =1. 答案:1合情推理与演绎推理1.合情推理类型定义特点归纳 推理由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理由部分到整体、由个别到一般 类比 推理 由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理由特殊到特殊 (1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.简言之,演绎推理是由一般到特殊的推理.(2)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的一般原理; ②小前提——所研究的特殊情况;③结论——根据一般原理,对特殊情况作出的判断. [小题速通]1.已知2和3都是无理数,试证:2+3也是无理数,某同学运用演绎推理证明如下:依题设2和3都是无理数,而无理数与无理数之和是无理数,所以2+3必是无理数.这个同学证明是错误的,错误原因是( )A .大前提错误B .小前提错误C .推理形式错误D .以上都可能解析:选A 大前提:无理数与无理数之和是无理数,错误; 小前提:2和3都是无理数,正确; 结论:2+3也是无理数,正确, 故只有大前提错误.2.我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线x 2a 2-y 2b2=1(a >0,b >0)与x 轴,直线y =h (h >0)及渐近线y =bax 所围成的阴影部分(如图)绕y 轴旋转一周所得的几何体的体积为________.解析:由题意可知,该几何体的横截面是一个圆环,设圆环的外半径与内半径分别为R ,r ,其面积S =π(R 2-r 2).∵x 2a 2-y 2b 2=1⇒R 2=a 2+a 2b 2y 2, 同理:r 2=a 2b2y 2,∴R 2-r 2=a 2,由祖暅原理知,此旋转体的体积等价于一个半径为a ,高为h 的柱体的体积,为πa 2h .答案:πa 2h 3.有如下等式: 2+4=6;8+10+12=14+16;18+20+22+24=26+28+30;……以此类推,则2 018出现在第________个等式中. 解析:①2+4=6; ②8+10+12=14+16;③18+20+22+24=26+28+30, ……其规律为:各等式首项分别为2×1,2×(1+3),2×(1+3+5),…, 所以第n 个等式的首项为2[1+3+…+(2n -1)]=2×n 1+2n -12=2n 2,当n =31时,等式的首项为2×312=1 922, 当n =32时,等式的首项为2×322=2 048, 所以2 018在第31个等式中. 答案:31证明方法1.直接证明 内容综合法分析法定义利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止实质由因导果执果索因框图表示P ⇒Q 1→Q 1⇒Q 2→…→Q n ⇒QQ ⇐P 1→P 1⇐P 2→…→得到一个明显成立的条件文字语言 因为……,所以…… 或由……,得……要证……,只需证……,即证……间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法. (1)反证法的定义:假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.(2)用反证法证明的一般步骤: ①反设——假设命题的结论不成立;②归谬——根据假设进行推理,直到推出矛盾为止; ③结论——断言假设不成立,从而肯定原命题的结论成立. [小题速通]1.(2018·成都一模)要证a 2+b 2-1-a 2b 2≤0,只需证明( ) A .2ab -1-a 2b 2≤0 B .a 2+b 2-1-a 4+b 42≤0C.a +b22-1-a 2b 2≤0D .(a 2-1)(b 2-1)≥0解析:选D a 2+b 2-1-a 2b 2≤0⇔(a 2-1)(b 2-1)≥0.2.观察(x 2)′=2x ,(x 4)′=4x 3,(cos x )′=-sin x ,由归纳推理可得:若定义在R 上的函数f (x )满足f (-x )=f (x ),记g (x )为f (x )的导函数,则g (-x )=( )A .f (x )B .-f (x )C .g (x )D .-g (x )解析:选D 由所给函数及其导数知,偶函数的导函数为奇函数,因此当f (x )是偶函数时,其导函数应为奇函数,故g (-x )=-g (x ).3.下列命题适合用反证法证明的是________.(填序号) ①已知函数f (x )=a x+x -2x +1(a >1),证明:方程f (x )=0没有负实数根; ②若x ,y ∈R ,x >0,y >0,且x +y >2, 求证:1+x y 和1+y x中至少有一个小于2;③关于x 的方程ax =b (a ≠0)的解是唯一的;④同一平面内,分别与两条相交直线垂直的两条直线必相交.解析:①是“否定”型命题,②是“至少”型命题,③是“唯一”型命题,且命题中条件较少,④中条件较少,不足以直接证明,因此四个命题都适合用反证法证明.答案:①②③④一、选择题1.若z =i(3-2i)(其中i 为复数单位),则z =( ) A .3-2i B .3+2i C .2+3iD .2-3i解析:选D 由z =i(3-2i)=2+3i ,得z =2-3i. 2.已知i 为虚数单位,a 为实数,复数z =a -3i1-i在复平面上对应的点在y 轴上,则a为( )A .-3B .-13C.13D .3解析:选A ∵z =a -3i1-i=a -3i1+i 1-i 1+i =a +3-3-a i2,又复数z =a -3i1-i在复平面上对应的点在y 轴上,∴⎩⎪⎨⎪⎧a +3=0,3-a ≠0,解得a =-3.3.分析法又称执果索因法,若用分析法证明“设a >b >c ,且a +b +c =0,求证:b 2-ac <3a ”索的因应是( )A .a -b >0B .a -c >0C .(a -b )(a -c )>0D .(a -b )(a -c )<0解析:选Cb 2-ac <3a ⇔b 2-ac <3a 2⇔(a +c )2-ac <3a 2⇔a 2+2ac +c 2-ac -3a 2<0⇔-2a 2+ac +c 2<0⇔2a 2-ac -c 2>0⇔(a -c )(2a +c )>0⇔(a -c )(a -b )>0.4.[n ]表示不超过 n 的最大整数. 若S 1=[ 1 ]+[ 2 ]+[ 3 ]=3,S 2=[ 4 ]+[ 5 ]+[ 6 ]+[7 ]+[8 ]=10,S 3=[9 ]+[10 ]+[11 ]+[12 ]+[13 ]+[14 ]+[15 ]=21,…… 则S n =( ) A .n (n +2)B .n (n +3)C .(n +1)2-1D .n (2n +1)解析:选D 观察得到:S n 是从n 2开始到n +12(不含)之前共2n +1个n 的和,所以S n 为n (2n +1).即[n 2]+[n 2+1]+[n 2+2]+…+[n +12-1]=n (2n +1).5.(2017·北京高考)执行如图所示的程序框图,输出的s 值为( )A .2 B.32 C.53D.85解析:选C 运行该程序,k =0,s =1,k <3;k =0+1=1,s =1+11=2,k <3; k =1+1=2,s =2+12=32,k <3; k =1+2=3,s =32+132=53,此时不满足循环条件,输出s ,故输出的s 值为53.6.若数列{a n }是等差数列,b n =a 1+a 2+…+a nn,则数列{b n }也为等差数列.类比这一性质可知,若正项数列{c n }是等比数列,且{d n }也是等比数列,则d n 的表达式应为( )A .d n =c 1+c 2+…+c nnB .d n =c 1·c 2·…·c nnC .d n = n c n 1+c n 2+…+c n nnD .d n =nc 1·c 2·…·c n解析:选D 因为数列{a n }是等差数列,所以b n =a 1+a 2+…+a n n =a 1+(n -1)·d2(d 为等差数列{a n }的公差),{b n }也为等差数列,因为正项数列{c n }是等比数列,设公比为q ,则d n =n c 1·c 2·…·c n =nc 1·c 1q ·…·c 1qn -1=c 1qn -12,所以{d n }也是等比数列.7.执行如图所示的程序框图,若输出的结果是99199,则判断框内应填的内容是( )A .n <98?B .n <99?C .n <100?D .n <101?解析:选B 由14n 2-1=12n -12n +1=1212n -1-12n +1, 可知程序框图的功能是计算并输出S =12⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1=12⎝ ⎛⎭⎪⎫1-12n +1=n 2n +1的值. 由题意令n 2n +1=99199,解得n =99,即当n <99时,执行循环体,若不满足此条件,则退出循环,输出S 的值.8.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )A .(7,5)B .(5,7)C .(2,10)D .(10,1)解:选B 依题意,把“整数对”的和相同的分为一组,不难得知第n 组中每个“整数对”的和均为n +1,且第n 组共有n 个“整数对”,这样的前n 组一共有n n +12个“整数对”,注意到10×10+12<60<11×11+12,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).二、填空题 9.M =1210+1210+1+1210+2+…+1211-1与1的大小关系为__________. 解析:因为M =1210+1210+1+1210+2+…+1211-1=1210+1210+1+1210+2+…+1210+210-1<1210+1210+1210+…+1210=1, 所以M <1. 答案:M <1 10.若复数z =a +ii(其中i 为虚数单位)的实部与虚部相等,则实数a =________.解析:因为复数z =a +i i =a i +i 2i2=1-a i ,所以-a =1,即a =-1. 答案:-111.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =________.解析:a =14,b =18.第一次循环:14≠18且14<18,b =18-14=4; 第二次循环:14≠4且14>4,a =14-4=10; 第三次循环:10≠4且10>4,a =10-4=6; 第四次循环:6≠4且6>4,a =6-4=2; 第五次循环:2≠4且2<4,b =4-2=2; 第六次循环:a =b =2,跳出循环,输出a =2. 答案:212.设n 为正整数,f (n )=1+12+13+…+1n ,计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,观察上述结果,可推测一般的结论为________.解析:∵f (21)=32,f (22)>2=42,f (23)>52,f (24)>62,∴归纳得f (2n)≥n +22(n ∈N *).答案:f (2n)≥n +22(n ∈N *)三、解答题13.若a >b >c >d >0且a +d =b +c , 求证:d +a <b +c . 证明:要证d +a <b +c , 只需证(d +a )2<(b +c )2, 即证a +d +2ad <b +c +2bc ,因为a +d =b +c ,所以只需证ad <bc ,即证ad <bc ,设a +d =b +c =t ,则ad -bc =(t -d )d -(t -c )c =(c -d )(c +d -t )<0, 故ad <bc 成立,从而d +a <b +c 成立.14.等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+3 2. (1)求数列{a n }的通项a n 与前n 项和S n ;(2)设b n =S n n(n ∈N *),求证:数列{b n }中任意不同的三项都不可能成为等比数列.解:(1)由已知得⎩⎨⎧a 1=1+2,3a 1+3d =9+32,所以d =2,故a n =2n -1+2,S n =n (n +2).(2)证明:由(1),得b n =S n n=n + 2.假设数列{b n }中存在三项b p ,b q ,b r (p ,q ,r 互不相等)成等比数列,则b 2q =b p b r ,即(q +2)2=(p +2)(r +2), 所以(q 2-pr )+2(2q -p -r )=0.因为p ,q ,r ∈N *,所以⎩⎪⎨⎪⎧q 2-pr =0,2q -p -r =0,所以⎝⎛⎭⎪⎫p +r 22=pr ,(p -r )2=0.所以p =r ,这与p ≠r 矛盾,所以数列{b n }中任意不同的三项都不可能成为等比数列. 高考研究课(一)算法与程序框图考查2类型——推结果、填条件 [全国卷5年命题分析]考点 考查频度 考查角度循环结构 5年10考 循环结构程序框图的输出功能及应用程序框图补条件 5年1考补全满足框图的条件程序框图的推结果问题[典例] a =-1,则输出的S =( )A.2 B.3C.4 D.5(2)(2017·山东高考)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )A.0,0 B.1,1C.0,1 D.1,0[解析] (1)运行程序框图,a=-1,S=0,K=1,K≤6成立;S=0+(-1)×1=-1,a=1,K=2,K≤6成立;S=-1+1×2=1,a=-1,K=3,K≤6成立;S=1+(-1)×3=-2,a=1,K=4,K≤6成立;S=-2+1×4=2,a=-1,K=5,K≤6成立;S=2+(-1)×5=-3,a=1,K=6,K≤6成立;S=-3+1×6=3,a=-1,K=7,K≤6不成立,输出S=3.(2)当输入x=7时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x成立,故a=1,输出a的值为1.当输入x=9时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x不成立且x 能被b 整除,故a =0,输出a 的值为0.[答案] (1)B (2)D [方法技巧]解决程序框图推结果问题要注意几个常用变量(1)计数变量:用来记录某个事件发生的次数,如i =i +1. (2)累加变量:用来计算数据之和,如S =S +i . (3)累乘变量:用来计算数据之积,如p =p ×i . [即时演练]1.(2016·全国卷Ⅰ)执行如图所示的程序框图,如果输入的x =0,y =1,n =1,则输出x ,y 的值满足( )A .y =2xB .y =3xC .y =4xD .y =5x解析:选C 输入x =0,y =1,n =1, 运行第一次,x =0,y =1,不满足x 2+y 2≥36; 运行第二次,x =12,y =2,不满足x 2+y 2≥36;运行第三次,x =32,y =6,满足x 2+y 2≥36,输出x =32,y =6.由于点⎝ ⎛⎭⎪⎫32,6在直线y =4x 上,故选C. 2.执行如图所示的程序框图,输出的s 是________.解析:第一次循环:i=1,s=1;第二次循环:i=2,s=-1;第三次循环:i=3,s =2;第四次循环:i=4,s=-2,此时i=5,执行s=3×(-2)=-6,故输出s=-6.答案:-6程序框图的补全及逆向求解问题[典例] (1)《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )A.4 B.5C.7 D.11(2)一个算法的程序框图如图所示,该程序输出的结果为3655,则空白处应填入的条件为( )A.i≤9? B.i≤6?C.i≥9? D.i≤8?[解析] (1)起始阶段有m=2a-3,i=1,第一次循环:m=2×(2a-3)-3=4a-9,i=2,第二次循环:m=2×(4a-9)-3=8a-21,i=3,第三次循环:m=2×(8a-21)-3=16a-45,i=4,第四次循环:m =2×(16a -45)-3=32a -93, 跳出循环,输出m =32a -93=35,解得a =4. (2)由1i i +2=12⎝ ⎛⎭⎪⎫1i -1i +2及题意知,该程序框图的功能是计算S =121-13+12-14+…+1i -1-1i +1+1i -1i +2=34-121i +1+1i +2的值,由S =3655,得i =9. 故空白处应填入的条件为:i ≤9. [答案] (1)A (2)A [方法技巧]程序框图的补全及逆向求解问题(1)先假设参数的判断条件满足或不满足;(2)运行循环结构,一直到运行结果与题目要求的输出结果相同为止; (3)根据此时各个变量的值,补全程序框图. [即时演练]1.执行如图所示的程序框图,若输出k 的值为16,则判断框内可填入的条件是( )A .S <1510?B .S >85?C .S >1510?D .S <85?解析:选D 运行程序:k =10,S =1;S =1110,k =11;S =1210,k =12;S =1310,k =13;S =1410,k =14;S =1510,k =15;S =1610=85,k =16,此时不满足条件,循环结束,输出k =16,所以判断框内可填入条件是S <85?.2.运行如图所示的程序框图,若输出的y 值的范围是[0,10],则输入的x 值的范围是________.解析:该程序的功能是计算分段函数的值, y =⎩⎪⎨⎪⎧3-x ,x <-1,x 2,-1≤x ≤1,x +1,x >1.当x <-1时,由0≤3-x ≤10,可得-7≤x <-1; 当-1≤x ≤1时,0≤x 2≤10成立;当x >1时,由0≤x +1≤10,可得1<x ≤9, 综上,输入的x 值的范围是[-7,9]. 答案:[-7,9]1.(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n ,那么在◇和▭两个空白框中,可以分别填入( )A .A >1 000和n =n +1B .A >1 000和n =n +2C .A ≤1 000和n =n +1D .A ≤1 000和n =n +2解析:选D 程序框图中A =3n-2n,且判断框内的条件不满足时输出n ,所以判断框中应填入A ≤1 000,由于初始值n =0,要求满足A =3n-2n>1 000的最小偶数,故执行框中应填入n =n +2.2.(2017·全国卷Ⅲ)执行如图所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5 B.4C.3 D.2解析:选D 执行程序框图,S=0+100=100,M=-10,t=2;S=100-10=90,M=1,t=3,S<91,输出S,此时,t=3不满足t≤N,所以输入的正整数N的最小值为2.3.(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )A.7 B.12C.17 D.34解析:选C 第一次运算:s=0×2+2=2,k=1;第二次运算:s=2×2+2=6,k=2;第三次运算:s=6×2+5=17,k=3>2,结束循环,s=17.4.(2016·全国卷Ⅲ)执行如图所示的程序框图,如果输入的a=4,b=6,那么输出的n =( )A.3 B.4C.5 D.6解析:选B 程序运行如下:开始a=4,b=6,n=0,s=0.第1次循环:a=2,b=4,a=6,s=6,n=1;第2次循环:a=-2,b=6,a=4,s=10,n=2;第3次循环:a=2,b=4,a=6,s=16,n=3;第4次循环:a=-2,b=6,a=4,s=20,n=4.此时,满足条件s>16,退出循环,输出n=4.故选B.5.(2015·全国卷Ⅰ)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )A .5B .6C .7D .8解析:选C 运行第一次:S =1-12=12=0.5,m =0.25,n =1,S >0.01;运行第二次:S =0.5-0.25=0.25,m =0.125,n =2,S >0.01; 运行第三次:S =0.25-0.125=0.125,m =0.062 5,n =3,S >0.01; 运行第四次:S =0.125-0.062 5=0.062 5,m =0.031 25,n =4,S >0.01; 运行第五次:S =0.031 25,m =0.015 625,n =5,S >0.01; 运行第六次:S =0.015 625,m =0.007 812 5,n =6,S >0.01; 运行第七次:S =0.007 812 5,m =0.003 906 25,n =7,S <0.01. 输出n =7.故选C.6.(2014·全国卷Ⅰ)执行如图所示程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M =( )A.203B.165C.72D.158解析:选D 第一次循环:M =32,a =2,b =32,n =2;第二次循环:M =83,a =32,b =83,n =3;第三次循环:M =158,a =83,b =158,n =4.则输出M =158.7.(2014·全国卷Ⅱ)执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A.4 B.5C.6 D.7解析:选D 执行循环体,第一次循环,M=2,S=5,k=2;第二次循环,M=2,S=7,k=3.故输出的S=7.一、选择题1.(2017·山东高考)执行如图所示的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )A.x>3 B.x>4C.x≤4 D.x≤5解析:选B 当x=4时,若执行“是”,则y=4+2=6,与题意矛盾;若执行“否”,则y=log24=2,满足题意,故应执行“否”.故判断框中的条件可能为x>4.2.执行如图所示的程序框图,若输入的a的值为2,则输出的b的值为( )A .-2B .1C .2D .4解析:选A 第一次循环,a =12,b =1,i =2;第二次循环,a =-1,b =-2,i =3;第三次循环,a =2,b =4,i =4;第四次循环,a =12,b =1,i =5;……;由此可知b 的值以3为周期出现,且当i =2 019时退出循环,此时共循环2 018次,又2 018=3×672+2,所以输出的b 的值为-2.3.某班有50名学生,在一次数学考试中,a n 表示学号为n 的学生的成绩,则执行如图所示的程序框图,下列结论正确的是( )A .P 表示成绩不高于60分的人数B .Q 表示成绩低于80分的人数C .R 表示成绩高于80分的人数D .Q 表示成绩不低于60分,且低于80分的人数解析:选D P 表示成绩低于60分的人数,Q 表示成绩低于80分且不低于60分的人数,R 表示成绩不低于80分的人数.4.(2017·天津高考)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为( )A .0B .1C .2D .3解析:选C 第一次循环,24能被3整除,N =243=8>3;第二次循环,8不能被3整除,N =8-1=7>3; 第三次循环,7不能被3整除,N =7-1=6>3; 第四次循环,6能被3整除,N =63=2<3,结束循环,故输出N 的值为2.5.执行如图所示的程序框图,则输出S 的值为( )A .3B .-6C .10D .-15解析:选D 第一次执行程序,得到S =0-12=-1,i =2; 第二次执行程序,得到S =-1+22=3,i =3; 第三次执行程序,得到S =3-32=-6,i =4; 第四次执行程序,得到S =-6+42=10,i =5; 第五次执行程序,得到S =10-52=-15,i =6, 结束循环,输出的S =-15.6.某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:组别(i)睡眠时间组中值(Z i)频数频率(P i)1[4.5,5.5)520.042[5.5,6.5)660.123[6.5,7.5)7200.404[7.5,8.5)8180.365[8.5,9.5)930.066[9.5,10.5)1010.02 现根据如下程序框图用计算机统计平均睡眠时间,则判断框①中应填入的条件是( )A.i>4? B.i>5?C.i>6? D.i>7?解析:选B 根据题目中程序框图,用计算机统计平均睡眠时间,总共执行6次循环,则判断框①中应填入的条件是i>5(或i≥6?).7.下图为某一函数的求值程序框图,根据框图,如果输出y的值为3,那么应输入x=( )A.1 B.2C.3 D.6解析:选B 该程序的作用是计算分段函数y =⎩⎪⎨⎪⎧x -3,x >66,2<x ≤6,5-x ,x ≤2的函数值,由题意,若x >6,则当y =3时,x -3=3,解得x =6,舍去; 若x ≤2,则当y =3时,5-x =3,解得x =2, 故输入的x 值为2.8.给出30个数:1,2,4,7,…,其规律是:第1个数是1;第2个数比第1个数大1;第3个数比第2个数大2;第4个数比第3个数大3,…,以此类推,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框①处和执行框②处应分别填入( )A .i ≤30?;p =p +i -1B .i ≤29?;p =p +i +1C .i ≤31?;p =p +iD .i ≤30?;p =p +i解析:选D 由于要计算30个数的和,故循环要执行30次,由于循环变量的初值为1,步长为1,故①中应填写“i ≤30?”.又由第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,故②中应填p =p +i .二、填空题9.(2017·江苏高考)如图是一个算法流程图.若输入x 的值为116,则输出y 的值是________.解析:由流程图可知其功能是运算分段函数y =⎩⎪⎨⎪⎧2x,x ≥1,2+log 2x ,0<x <1,所以当输入的x的值为116时,y =2+log 2116=2-4=-2.答案:-210.按下列程序框图来计算:如果输入的x =5,则应该运算________次才停止. 解析:由题意,该程序按如下步骤运行:经过第一次循环得到x =3×5-2=13,不满足x >200,进入下一步循环; 经过第二次循环得到x =3×13-2=37,不满足x >200,进入下一步循环; 经过第三次循环得到x =3×37-2=109,不满足x >200,进入下一步循环; 经过第四次循环得到x =3×109-2=325,因为325>200,结束循环并输出x 的值 因此,运算进行了4次后,输出x 值而程序停止.故答案为4. 答案:411.中国古代有计算多项式值的秦九韶算法,该算法的程序框图如图所示. 执行该程序框图,若输入的x =3,n =3,输入的a 依次为由小到大顺序排列的质数(从最小质数开始),直到结束为止,则输出的s =________.解析:运行程序:x =3,n =3,k =0,s =0;a =2,s =2,k =1;a =3,s =9,k =2;a =5,s =32,k =3;a =7,s =103,k =4,此时满足条件,循环结束,输出s =103.答案:10312.阅读如图所示的程序框图,运行相应的程序,输出的结果是a =________.解析:运行程序,可得a=10,i=1,不满足i≥5,不满足a是奇数,a=5,i=2,不满足i≥5,满足a是奇数,a=16,i=3,不满足i≥5,不满足a是奇数,a=8,i=4,不满足i≥5,不满足a是奇数,a=4,i=5,满足i≥5,退出循环,输出a的值为4.答案:413.已知某程序框图如图所示,则程序运行结束时输出的结果为________.解析:第一次循环结束时,n=2,x=3,y=1;第二次循环结束时,n=4,x=9,y=3;第三次循环结束时,n=6,x=27,y=3.此时满足n>4,结束循环,输出log y x=log327=3.答案:314.(2018·黄山调研)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=________.解析:第一次循环,得S =2;第二次循环,得n =2,a =12,A =2,S =92;第三次循环,得n =3,a =14,A =4,S =354;第四次循环,得n =4,a =18,A =8,S =1358>10,结束循环,输出的n =4.答案:41.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A 1,A 2,…,A 16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )图1图2A .6B .7C .10D .16解析:选C 由程序框图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知,数学成绩大于等于90的人数为10,因此输出结果为10.2.如果执行程序框图,如果输出的S=2 550,则判断框内应填入的条件是( )A.k≤50? B.k≥51?C.k<50? D.k>51?解析:选A 根据题中的程序框图,可得该程序经过第一次循环得到S=2,k=2;经过第二次循环得到S=2+4,k=3;经过第三次循环得到S=2+4+6,k=4;……设经过第n次循环得到2+4+6+…+2n=n2+n=2 550,解得n=50,由此说明,当n>50时不满足判断框中的条件,则正好输出S=2 550,∴判断框应填入的条件是k≤50?.高考研究课(二)数系的扩充与复数的引入的命题3角度——概念、运算、意义[全国卷5年命题分析]考点考查频度考查角度复数的有关概念5年4考虚部、模等有关概念与运算结合考查复数的几何意义5年2考与运算结合考查几何意义复数的运算5年6考考查乘法、除法、幂的运算复数的有关概念(a∈R)是纯虚数,则a的值为( ) [典例] (1)设i是虚数单位.若复数a-3-iA.-3 B.-1C.1 D.3(2)已知复数z 满足z1+i =|2-i|,则z 的共轭复数对应的点位于复平面内的( )A .第一象限B .第二象限C .第三象限D .第四象限(3)若复数 z 满足z (1+i)=2i(i 为虚数单位),则|z |=( ) A .1 B .2C. 2D. 3[解析] (1)∵复数a -103-i =a -103+i10=(a -3)-i 为纯虚数,∴a -3=0,∴a =3.(2)∵z1+i=|2-i|=5,∴z =5+5i ,则z 的共轭复数5-5i 对应的点(5,-5)位于复平面内的第四象限.(3)法一:设z =a +b i(a ,b ∈R),则由z (1+i)=2i ,得(a +b i)·(1+i)=2i ,所以(a-b )+(a +b )i =2i ,由复数相等的条件得⎩⎪⎨⎪⎧a -b =0,a +b =2,解得a =b =1,所以z =1+i ,故|z |=12+12= 2.法二:由z (1+i)=2i ,得z =2i 1+i =2i1-i 2=i -i 2=1+i ,所以|z |=12+12= 2. [答案] (1)D (2)D (3)C [方法技巧]求解与复数概念相关问题的技巧复数的分类、复数的相等、复数的模,共轭复数的概念都与复数的实部与虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即a +b i(a ,b ∈R)的形式,再根据题意求解.[即时演练]1.(2017·山东高考)已知a ∈R ,i 是虚数单位.若z =a + 3 i ,z ·z =4,则a =( ) A .1或-1 B.7或-7 C .- 3 D. 3解析:选A 法一:由题意可知z =a -3i ,∴z ·z =(a +3i)(a -3i)=a 2+3=4,故a =1或-1. 法二:z ·z =|z |2=a 2+3=4,故a =1或-1.2.若复数2+a i1-i (a ∈R)是纯虚数(i 是虚数单位),则复数z =a +(a -3)i 在复平面内对应的点位于第________象限.解析:∵2+a i1-i =2+a i1+i 1-i1+i =2-a +2+a i 2=2-a 2+2+a2i 是纯虚数,∴⎩⎪⎨⎪⎧2-a 2=0,2+a 2≠0,解得a =2.∴z =2-i ,在复平面内对应的点(2,-1)位于第四象限. 答案:四3.(2017·浙江高考)已知a ,b ∈R ,(a +b i)2=3+4i(i 是虚数单位),则a 2+b 2=________,ab =________.解析:∵(a +b i)2=a 2-b 2+2ab i =3+4i ,∴⎩⎪⎨⎪⎧a 2-b 2=3,2ab =4,∴⎩⎪⎨⎪⎧a =2,b =1或⎩⎪⎨⎪⎧a =-2,b =-1,∴a 2+b 2=5,ab =2. 答案:5 2复数的代数运算[典例] (1)i 为虚数单位,则⎝ ⎛⎭⎪⎫1+i 2 018=( )A .-iB .-1C .iD .1(2)(2017·全国卷Ⅱ)3+i1+i =( )A .1+2iB .1-2iC .2+iD .2-i(3)(2017·全国卷Ⅱ)(1+i)(2+i)=( ) A .1-i B .1+3i C .3+iD .3+3i[解析] (1)∵1-i 1+i =1-i 21+i 1-i =1-2i -12=-i ,∴⎝⎛⎭⎪⎫1-i 1+i 2 018=(-i)2 018=(-i)2 016·(-i)2=-1.(2)3+i 1+i=3+i 1-i 1+i1-i =4-2i2=2-i. (3)(1+i)(2+i)=2+i 2+3i =1+3i. [答案] (1)B (2)D (3)B [方法技巧]复数代数形式运算问题的解题策略(1)复数的乘法复数的乘法类似于多项式的四则运算,可将含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可.(2)复数的除法除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式. [提醒] 在进行复数的代数运算时,记住以下结论,可提高计算速度. (1)(1±i)2=±2i;1+i 1-i =i ;1-i 1+i =-i ;(2)-b +a i =i(a +b i); (3)i 4n=1,i 4n +1=i ,i4n +2=-1,i4n +3=-i ,i 4n+i4n +1+i4n +2+i 4n +3=0,n ∈N *.[即时演练]1.设复数z =1+i(i 是虚数单位),则2z+z 2=( )A .1+iB .1-iC .-1-iD .-1+i解析:选A 2z +z 2=21+i +(1+i)2=1-i +2i =1+i.2.已知复数z =3+i 1-3i 2,z 是z 的共轭复数,则z ·z =________.解析:∵z =3+i 1-3i 2=3+i-2-23i=3+i -21+3i =3+i1-3i -21+3i1-3i=23-2i -8=-34+14i , 故z =-34-14i ,∴z ·z =⎝ ⎛⎭⎪⎫-34+14i ⎝ ⎛⎭⎪⎫-34-14i =316+116=14. 答案:143.已知i 是虚数单位,⎝ ⎛⎭⎪⎫21-i 2 018+⎝ ⎛⎭⎪⎫1+i 1-i 6=________.解析:原式=⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫21-i 2 1 009+⎝ ⎛⎭⎪⎫1+i 1-i 6=⎝ ⎛⎭⎪⎫2-2i 1 009+i 6=i 1 009+i 6=i4×252+1+i 4+2=i +i 2=-1+i.答案:-1+i复数的几何意义[典例] (1)已知复数z =a +i(a ∈R).若|z |<2,则z +i 2在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限(2)(2017·北京高考)若复数(1-i)(a +i)在复平面内对应的点在第二象限,则实数a 的取值范围是( )A .(-∞,1)B .(-∞,-1)C .(1,+∞)D .(-1,+∞)[解析] (1)因为复数z =a +i(a ∈R).若|z |<2,则a 2+1<2,解得-1<a <1,所以z +i 2=a -1+i 在复平面内对应的点(a -1,1)位于第二象限.(2)复数(1-i)(a +i)=a +1+(1-a )i , 其在复平面内对应的点(a +1,1-a )在第二象限,故⎩⎪⎨⎪⎧a +1<0,1-a >0,解得a <-1.[答案] (1)B (2)B [方法技巧](1)复数z 、复平面上的点Z 及向量OZ ―→相互联系,即z =a +b i(a ,b ∈R)⇔Z (a ,b )⇔OZ ―→. (2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.[即时演练]1.如图,若向量OZ ―→对应的复数为z ,则z +4z表示的复数为( )A .1+3iB .-3-iC .3-iD .3+i解析:选 D 由图可得Z (1,-1),即z =1-i ,所以z +4z =1-i +41-i =1-i +41+i 1-i 1+i =1-i +4+4i2=1-i +2+2i =3+i.2.若z =(a -2)+(a +1)i 在复平面内对应的点在第二象限,则实数a 的取值范围是________.解析:∵z =(a -2)+(a +1)i 在复平面内对应的点在第二象限,∴⎩⎪⎨⎪⎧a -2<0,a +1>0,解得-1<a <2.即实数a 的取值范围是(-1,2). 答案:(-1,2)1.(2017·全国卷Ⅰ)设有下面四个命题:p 1:若复数z 满足1z ∈R ,则z ∈R ;p 2:若复数z 满足z 2∈R ,则z ∈R ; p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=z 2; p 4:若复数z ∈R ,则z ∈R.其中的真命题为( ) A .p 1,p 3 B .p 1,p 4 C .p 2,p 3D .p 2,p 4解析:选B 设复数z =a +b i(a ,b ∈R),对于p 1,∵1z =1a +b i =a -b ia 2+b 2∈R ,∴b =0,∴z ∈R ,∴p 1是真命题;对于p 2,∵z 2=(a +b i)2=a 2-b 2+2ab i ∈R ,∴ab =0,∴a =0或b =0,∴p 2不是真命题; 对于p 3,设z 1=x +y i(x ,y ∈R),z 2=c +d i(c ,d ∈R),则z 1z 2=(x +y i)(c +d i)=cx。

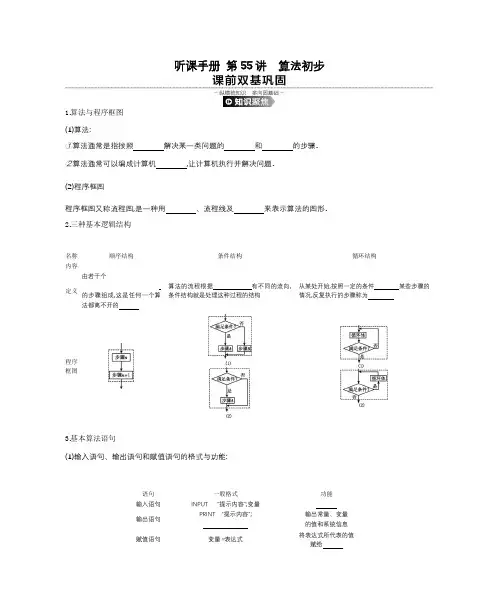
听课手册第55讲算法初步1.算法与程序框图(1)算法:①算法通常是指按照解决某一类问题的和的步骤.②算法通常可以编成计算机,让计算机执行并解决问题.(2)程序框图程序框图又称流程图,是一种用、流程线及来表示算法的图形.2.三种基本逻辑结构名称内容顺序结构条件结构循环结构定义由若干个的步骤组成,这是任何一个算法都离不开的算法的流程根据有不同的流向,条件结构就是处理这种过程的结构从某处开始,按照一定的条件某些步骤的情况,反复执行的步骤称为程序框图3.基本算法语句(1)输入语句、输出语句和赋值语句的格式与功能:语句一般格式功能输入语句INPUT“提示内容”;变量输出语句PRINT“提示内容”;输出常量、变量的值和系统信息赋值语句变量=表达式将表达式所代表的值赋给(2)条件语句的格式及框图:①IF-THEN格式:图10-55-1②IF-THEN-ELSE格式:图10-55-2(3)循环语句的格式及框图:①UNTIL语句:图10-55-3②WHILE语句:图10-55-4题组一常识题1.[教材改编]如图10-55-5所示的程序框图中含有顺序结构和结构,执行此程序框图,则输出S的值为.图10-55-5图10-55-62.[教材改编]执行如图10-55-6所示的程序框图,则输出s的值为.图10-55-73.[教材改编]如图10-55-7为计算y=|x|的函数值的程序框图,则此程序框图中的判断框内应填.题组二常错题◆索引:分不清程序框图是条件结构还是循环结构致错;把握不好循环结构中控制循环的条件致错.4.执行如图10-55-8所示的程序框图,它的功能是.若输出的y值的范围是[0,10],则输入的x值的范围是.图10-55-8图10-55-95.秦九韶是我国南宋时期著名的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图10-55-9所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入整数n的值为.6.执行如图10-55-10所示的程序框图,若输入k的值为3,则输出S的值为.图10-55-10图10-55-117.执行如图10-55-11所示的程序框图,输出的s值为.探究点一算法的基本结构例1(1)[2017·全国卷Ⅱ]执行如图10-55-12所示的程序框图,如果输入的a=-1,则输出的S=()A.2B.3C.4D.5,则输出y的值是.(2)[2017·江苏卷]图10-55-13是一个算法流程图.若输入x的值为116图10-55-12图10-55-13[总结反思]高考对算法初步的考查主要是对程序框图含义的理解与运用,重点应放在读懂框图上,尤其是条件结构、循环结构.特别要注意条件结构中条件的判断,对于循环结构要搞清进入或退出循环的条件、循环的次数,这是解题的关键.按流程线依次执行各框,是解题的基本思路.变式题(1)[2018·甘肃西北师大附中诊断]某程序框图如图10-55-14所示,若输出的s=57,则判断框内可以填()A.k>4?B.k>5?C.k>6?D.k>7?图10-55-14图10-55-15(2)执行如图10-55-15所示的程序框图,则输出x的值为()A. 12B. 10C. 9D. 8探究点二算法的交汇性问题例2(1)[2018·广西钦州质检]执行如图10-55-16所示的程序框图,输入正整数n(n≥2)和数据a1,a2,…,a n,如果输出的s是数据a1,a2,…,a n的平均数,则程序框图的处理框★处应填写的是()A.s=is+a ii B.s=(i-1)s+a iiC.s=(i-1)s+a ii-1D.s=is+a ii-1图10-55-16图10-55-17(2)执行如图10-55-17所示的程序框图,若输入n的值为3,则输出的S的值为.[总结反思]与其他知识交汇的程序框图问题,主要涉及数列求和、三角函数的计算、函数、统计等问题,注意观察是否能利用数列的求和公式、三角函数的周期性等知识解决问题.变式题(1)[2018·河南安阳二模]若执行如图10-55-18所示的程序框图,其中rand[0,1]表示区间[0,1]上任意一个实数,则输出数对(x,y)的概率为()A.12B.π6C.π4D.√32图10-55-18图10-55-19(2)执行如图10-55-19所示的程序框图,若输入的x值的取值范围是[-1,4],则输出y值的取值范围是()A. [-1,2]B. [-1,15]C. [0,2]D. [2,15]探究点三基本算法语句例3运行如图10-55-20所示的程序,若输出y的值为1,则输入x的值为()INPUT xIF x>=0THENy=2∧xELSEy=ABS(x)END IFPRINT yEND图10-55-20A. 0B. 0或-1C. ±1D. 1[总结反思]算法语句应用的四个关注点:(1)输入、输出语句:在输入、输出语句中加提示信息时,要加引号,变量之间用逗号隔开.(2)赋值语句:左、右两边不能对换,赋值号左边只能是变量.(3)条件语句:要分清条件语句的内外条件结构,保证结构的完整性.(4)循环语句:分清“UNTIL”语句和“WHILE”语句的格式与特征,不能混用.变式题(1)如图10-55-21为一个求20个数的平均数的程序,则横线上应填充的语句为()S=0i=1DOINPUT xS=S+xi=i+1LOOP UNTILa=S/20PRINT aEND图10-55-21A. i>20B. i<20C. i>=20D. i<=20(2)[2018·河北保定模拟]根据如图10-55-22所示的程序,可知输出的结果为S= .S=1i=1WHILE i<8S=S+2i=i+3WENDPRINT SEND图10-55-22完成课时作业(五十五)。



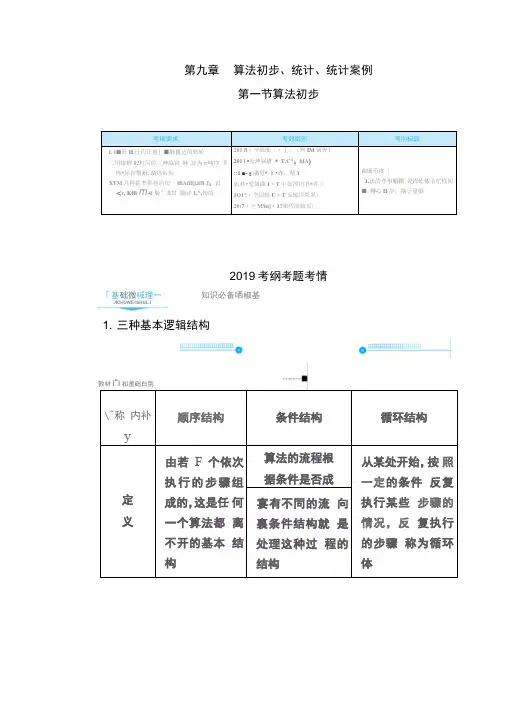
第九章算法初步、统计、统计案例第一节算法初步2019考纲考题考情「基础微械理一知识必备哂椒基JICHUWE1SHUL.I1. 三种基本逻辑结构\^称内补y顺序结构条件结构循环结构定义由若F个依次执行的步骤组成的,这是任何一个算法都离不开的基本结构算法的流程根据条件是否成从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体宴有不同的流向裏条件结构就是处理这种过程的结构考纲要求考鈕举创考向标諾L i■昴H辻约比亶」■辭篦适的黠轮二用钳輕1?杠闪的三呻临宮時詰为r吨序蒂枸*殆件塔耐.漪炜帖恂XTM几种甚杰舞祂谄旬一ffiAifitj.iffi J:识<r, Kffi m 4i梟”谍冒圖评1,",旬的201 fi・全個淮||・[;〔判IM第悴}201 i •无坤届唐* T,C^;hiA)::1 ■- g満号* 1 •亦;閘1如林•愛国曲1・T屮如押川书*件>JO1?・全国軽U・T显输川犁累〉20)7・全M$nj・1?崔竹战蜡果)曲販币度「1.法的苓事箱钳瓷挥屹怖主忙性闻■ 轉心H岸;抽亍盘損敦材I“I扣垄础白別2•算法的特征概括性、逻辑性、有穷性、不唯一性、普遍性。
语句一般格式功能输人语句INPUT"提示内容J变量输入信息输出语句PRINT提示内容S表达式输出常量、变量的值和系统信息赋值语句变量=表达式将表达式的值赋给变量4•条件语句(1) 算法中的条件结构与条件语句相对应。
(2) 条件语句的格式及框图。
①IF —THEN格式:5.循环语句(1)算法中的循环结构与循环语句相对应。
⑵循环语句的格式及框图。
①UNTIL语句:IX)循环体UN I IL 条件②WHILE语句:1.赋值号左边只能是变量(不能是表达式),在一个赋值语句中只能给一个变量赋值。
2. 直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相题纠徴谢身-TIZl WEIRESHEN一、走进教材1.(必修3P25例5改编)如图为计算y= |x|函数值的程序框图,则此程序框图中的判断框内应填___________ 。



第1讲 算法初步基础知识整合1.算法的框图及结构 (1)算法算法通常是指按照一定□01规则解决某一类问题的□02明确程序或有限的步骤.这些程序或步骤必须是□03明确和□04有效的,而且能够在有限步之内完成. (2)程序框图程序框图又称□05流程图,是一种用□06程序框、□07流程线及□08文字说明来表示算法的图形.通常,程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一个步骤;□09流程线带有方向箭头,按照算法进行的顺序将□10程序框连接起来. (3)三种基本逻辑结构(1)输入语句、输出语句、赋值语句的格式与功能(2)条件语句的格式及框图(3)循环语句的格式及框图1.注意区分处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.2.循环结构中必有条件结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.3.注意区分当型循环与直到型循环.直到型循环是“先循环,后判断,条件满足时终止循环”,而当型循环则是“先判断,后循环,条件满足时执行循环”.两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.1.(2018·北京高考)执行如图所示的程序框图,输出的s值为( )A.12B.56 C.76 D.712答案 B解析 初始化数值k =1,s =1,循环结果执行如下:第一次:s =1+(-1)1·12=12,k=2,k =2≥3不成立;第二次:s =12+(-1)2·13=56,k =3,k =3≥3成立,循环结束,输出s =56,故选B.2.下列程序段执行后,变量a ,b 的值分别为( )a =15b =20a =a +bb =a -b a =a -b PRINT a ,bA .20,15B .35,35C .5,5D .-5,-5 答案 A解析 a =15,b =20,把a +b 赋给a ,因此得出a =35,再把a -b 赋给b ,即b =35-20=15.再把a -b 赋给a ,此时a =35-15=20,因此最后输出的a ,b 的值分别为20,15.故选A.3.(2019·武昌调研)执行如图所示的程序框图,如果输入的a 依次为2,2,5时,输出的S 为17,那么在判断框中可以填入( )A .k >nB .k <nC .k ≥nD .k ≤n 答案 A解析 第一次输入a =2,此时S =0×2+2=2,k =0+1=1,不满足k =1>n =2;第二次输入a =2,此时S =2×2+2=6,k =1+1=2,不满足k =2>n =2;第三次输入a =5,此时S =6×2+5=17,k =2+1=3,满足k =3>n =2,循环终止,输出的S =17.故选A.4.(2019·湖南模拟)执行如图所示的程序框图,输出S 的值为12时,k 是( )A .5B .3C .4D .2 答案 A解析 模拟执行程序,可得每次循环的结果依次为:k =2,k =3,k =4,k =5,大于4,可得S =sin 5π6=12,输出S 的值为12.故选A.5.(2019·锦州二检)若如图所示的程序框图输出的S 是30,则在判断框中M 表示的“条件”应该是( )A.n≥3 B.n≥4 C.n≥5 D.n≥6答案 B解析第一次循环,n=1,S=2;第二次循环,n=2,S=6;第三次循环,n=3,S=14;第四次循环,n=4,S=30,故选B.6.执行如图所示的程序框图,若输入x的值为1,则输出n的值为________.答案 3解析第一次:x=1,x2-4x+3=0≤0.第二次:x=2,n=1,x2-4x+3=-1≤0.第三次:x=3,n=2,x2-4x+3=0≤0.第四次:x=4,n=3,x2-4x+3=3>0.此时程序结束.核心考向突破考向一算法的基本结构例1 (2018·天津高考)阅读右边的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( )A .1B .2C .3D .4 答案 B解析 结合流程图运行程序如下:首先初始化数据:N =20,i =2,T =0,N i =202=10,结果为整数,执行T =T +1=1,i=i +1=3,此时不满足i ≥5;N i =203,结果不为整数,执行i =i +1=4,此时不满足i ≥5;N i =204=5,结果为整数,执行T =T +1=2,i =i +1=5,此时满足i ≥5;跳出循环,输出T =2.故选B.触类旁通利用循环结构表示算法应注意的问题(1)注意是利用当型循环结构,还是直到型循环结构.注意选择准确地表示累计的变量.注意在哪一步开始循环,满足什么条件不再执行循环体.即时训练 1.当m =7,n =3时,执行如右图所示的程序框图,输出的S 的值为( )A .7B .42C .210D .840 答案 C解析 m =7,n =3,k =7,S =1,不满足k <m -n +1;S =1×7=7,k =6,不满足k <m -n +1;S =7×6=42,k =5,不满足k <m -n +1;S =42×5=210,k =4,满足k <m -n +1,退出循环,输出的S 的值为210.2.若执行如图所示的程序框图,输出的S 的值为4,则判断框中应填入的条件是( )A.k<18 B.k<17 C.k<16 D.k<15答案 C解析由程序框图,得S=1·log23·log34·log45·…·log k(k+1)=log2(k+1)=4,解得k=15,此时k=15+1=16,循环终止.所以判断框中应填入的条件是k<16,故选C.考向二算法的交汇性问题角度1算法与函数的交汇例2 (2019·郑州模拟)执行如图所示的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]答案 A解析当-1≤t<1时,s=3t,则s∈[-3,3).当1≤t≤3时,s=4t-t2.函数在[1,2]上单调递增,在[2,3]上单调递减.∴s∈[3,4].综上知s∈[-3,4].故选A.角度2算法与数列的交汇例3 执行如图所示的程序框图,则输出的k=( )A .7B .8C .9D .10 答案 C解析 由程序框图可知,当k =1时,s =11×2,当k =2时,s =11×2+12×3,当k =n时,s =11×2+12×3+…+1nn +=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1,由1-1n +1≥910⇒n ≥9,即当k =9时,s =910.故选C. 角度3 算法与统计的交汇例4 (2019·九江联考)图1是随机抽取的15户居民月均用水量(单位:吨)的茎叶图,月均用水量依次记为A 1,A 2,…,A 15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,则输出的n 的值为________.答案 7解析 由程序框图知,算法的功能是计算15户居民中月均用水量大于2.1的户数,由茎叶图得,在这15户居民中,月均用水量大于2.1的户数为7,∴输出的n 的值为7.触类旁通解决算法的交汇性问题的方法循环结构的程序框图与数列、不等式、统计等知识综合是高考命题的一个热点,解决此类问题时应把握三点:一是初始值,即计数变量与累加变量的初始值;二是两个语句,即循环结构中关于计数变量与累加变量的赋值语句;三是一个条件,即循环结束的条件,注意条件与流程线的对应关系.即时训练 3.(2019·宁夏模拟)执行如图所示的程序框图,如果输入的t ∈[-2,2],则输出的S 属于( )A .[-6,-2]B .[-5,-1]C .[-4,5]D .[-3,6]答案 D解析 当0≤t ≤2时,S =t -3∈[-3,-1].当-2≤t <0时,2t 2+1∈(1,9],则S ∈(-2,6].综上,当-2≤t ≤2时,S ∈[-3,6],故选D.4.(2019·湖南长沙模拟)如图,给出的是计算1+14+17+…+1100的值的一个程序框图,则图中判断框内的(1)处和执行框中的(2)处应填的语句是( )A .i >100,n =n +1B .i <34,n =n +3C .i >34,n =n +3D .i ≥34,n =n +3 答案 C解析 算法的功能是计算1+14+17+…+1100的值,易知1,4,7,…,100成等差数列,公差为3,所以执行框中的(2)处应为n =n +3,令1+(i -1)×3=100,解得i =34,∴终止程序运行的i 值为35,∴判断框内的(1)处应为i >34,故选C.5.在2018~2019赛季NBA 季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中x 是这7场比赛的平均得分),求输出的σ的值.解 由题知x =17(100+104+98+105+97+96+100)=100,由算法流程图可知s =(100-100)2+(104-100)2+(98-100)2+(105-100)2+(97-100)2+(96-100)2+(100-100)2=70.故σ=s7=10. 考向三 基本算法语句例5 (1)(2019·福建质检)下列程序语句的算法功能是( )INPUT a ,b ,c IF a<b THEN a =b END IFIF a<c THEN a =c END IF PRINT a ENDA .输出a ,b ,c 三个数中的最大数B .输出a ,b ,c 三个数中的最小数C .将a ,b ,c 从小到大排列D .将a ,b ,c 从大到小排列 答案 A解析 由程序语句可知,当比较a ,b 的大小后,选择较大的数赋给a ;当比较a ,c 的大小后,选择较大的数赋给a,最后输出a,所以此程序的作用是输出a,b,c中最大的数.故选A.(2)运行下面的程序,执行后输出的s的值是( )A.11 B.15 C.17 D.19答案 B解析当i=3时,s=7,当i=5时,s=11,当i=7时,s=15,此时不满足“i<6”,所以输出s=15,故选B.触类旁通基本算法语句应用中需注意的问题(1)赋值号“=”的左、右两边不能对调,A=B和B=A的含义及运行结果是不同的.不能利用赋值语句进行代数式的演算如化简、因式分解等,在赋值语句中的赋值号右边的表达式中每一个“变量”都必须事先赋给确定的值.赋值号与数学中的等号意义不同,比如在数学中式子N=N+1一般是错误的,但在赋值语句中它的作用是将原有的N的值加上1再赋给变量N,这样原来的值被“冲”掉.即时训练 6.阅读下面的程序:如果上述程序输入的值是51,则运行结果是( ) A .51 B .15 C .105 D .501 答案 B解析 因为51÷10=5……1,所以a =5,b =1,x =10×1+5=15.故选B.7.(2019·龙岩质检)如图所示的程序,若最终输出的结果为6364,则在程序中横线____?____处应填入的语句为( )答案 B 解析。
2020年高考文科数学《算法初步与复数》题型归纳与训练【题型归纳】题型一 算法的基本结构例1 :执行如图所示的程序框图,输出的s 值为( )A .12B .56C .76D .712【答案】B【解析】运行程序框图,k =l ,s =1;1111(1)22s =+-⨯=,2k =;2115(1)236s =+-⨯=,k =3;满足条件,跳出循环,输出的56s =,故选B .【易错点】看错条件【思维点拨】一步一步来,跳出循环结束例2 :阅读如图的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )A .1B .2C . 3D .4【答案】B【解析】20N =,2i =,0T =,20102N i ==,是整数;011T =+=,213i =+=,35<,203N i =,不是整数;314i =+=,45<,2054N i ==,是整数;112T =+=,415i =+=,结束循环,输出的2T =,故选B .【易错点】计算【思维点拨】一步一步来,跳出循环结束 题型二 算法中的条件缺失问题 例3:为计算11111123499100=-+-++-…S ,设计了如图的程序框图,则在空白框中应填入( ) A .1=+i i B .2=+i i C .3=+i i D .4=+i i 【答案】B【解析】由程序框图的算法功能知执行框1=+N N i计算的是连续奇数的倒数和,而执行框11=++T T i 计算的是连续偶数的倒数和,所以在空白执行框中应填入的命令是2=+i i ,故选B .【易错点】学生入手较难,不好想【思维点拨】难度较大,需要找规律发现问题 题型三 算法的交汇性问题例4:下面程序框图是为了求出满足321000n n ->的最小偶数n可以分别填入A .1000A >和1n n =+B .1000A >和2n n =+C .1000A ≤和1n n =+D .1000A ≤和2n n =+ 【答案】D【解析】由题意选择321000n n ->,则判定框内填1000A ≤,由因为选择偶数,所以矩形框内填2n n =+,故选D. 【易错点】没看懂题目【思维点拨】巧妙利用偶数解决问题 题型四 复数的有关概念 例5:()i 23i +=( ) A .32i -B .32i +C .32i --D .32i -+【答案】D【解析】()i 23i 32i +=-+,故选D . 【易错点】计算失误【思维点拨】最基本的运算考查 例6:若,则||zz =( ) A .1 B .C .D .【答案】D 【解析】43||55z i z ==-,故选D . 【易错点】分式计算失误【思维点拨】计算复数模的运算,共轭复数的考查43i z =+1-43i 55+43i 55-题型五 复数的几何意义例7:复平面内表示复数i(2i)z =-+的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】C【解析】∵i(2i)12i z =-+=--,∴复数z 在复平面内对应的点(1,2)Z --,位于第三象限,选C . 【易错点】忘记复数对应点的坐标【思维点拨】先化简,再写坐标,对应找象限例8:若复数(1i)(i)a -+在复平面内对应的点在第二象限,则实数a 的取值范围是( )A .(,1)-∞B .(,1)-∞-C .(1,)+∞D .(1,)-+∞ 【答案】B【解析】(1i)(i)(1)(1)i z a a a =-+=++-,因为对应的点在第二象限,∴,解得,故选B.【易错点】象限点的特征弄错【思维点拨】先化简,再写坐标,列出不等式解出即可【巩固训练】题型一 算法的基本结构1.执行如图所示的程序框图,输出的s 值为( )A .2B .32 C .53D .85 【答案】C【解析】0k =时,03<成立,第一次进入循环1k =,2s =,13<成立;第二次进入循环,2k =,32s =,23<成立;第三次进入循环3k =,53s =,33<否,输出53s =,选C .2.执行如图的程序框图,如果输入的011x y n ===,,,则输出x ,y 的值满足( )A .2y x =B .3y x =C .4y x =D .5y x =1010a a +<⎧⎨->⎩1a <-【答案】C【解析】运行程序,第1次循环得0,1,2x y n ===,第2次循环得1,2,32x y n ===,第3次循环得3,62x y ==,此时2236x y +…,输出,x y ,满足C 选项.3.执行如图所示的程序框图,如果输入3n =,则输出的S =( )A .67 B .37 C .89 D .49【答案】B【解析】第一次循环,113S =⨯,此时2i =,不满足条件, 继续第二次循环111335S =+⨯⨯,此时3i =,不满足条件, 继续第三次循环11131335577S =++=⨯⨯⨯,此时43i =>,退出循环,输出S 的值为37,选B .题型二 算法中的条件缺失问题1.执行如图所示的程序框图,若输出k 值为8,则判断框内可填入的条件是( )A .34s ≤B .56s ≤ C .1112s ≤ D .2524s ≤【答案】C【解析】由程序框图,k 的值依次为0,2,4,6,8,因此1111124612S =++=(此时6k =)还必须计算一次, 因此可填1112S ≤,选C .2.执行如如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .12s >B .35s > C .710s > D .45s > 【答案】C【解析】当输出6k =时,98771109810s =⨯⨯⨯=,结合题中的程序框图知,选3.某程序框图如图所示,若输出的S =57,则判断框内为( )A .k >4?B .k >5?C .k >6?D .k >7? 【答案】A【解析】第一次执行后,2,224k S ==+=;第二次执行后,3,8311k S ==+=;第三次执行后,4,22426k S ==+=; 第四次执行后,5,52557k S ==+=;自此循环结束,故判断框中填4?k >.题型三 算法的交汇性问题1.某程序框图如图所示,若该程序运行后输出的值是,则( )A .B .C .D .【答案】A【解析】 ; 输出的结果为,此时,故. 594=a 5=a 6=a 7=a 13151,11;2,11;2233k s k s ==+-===+-=17193,11;4,114455k s k s ==+-===+-=595k a =>4a =2.执行如图程序框图,如果输入的,则输出s 属于( ) A .[-3,4] B .[-5,2] C .[-4,3] D .[-2,5] 【答案】A【解析】由题意知,当时,,当时,,∴输出s 属于[-3,4],故选.3.如图为某算法的程序框图,则程序运行后输出的结果是_________.【答案】3【解析】由程序框图可知:第一次:T=0,k=1,sin1sin 002π=>=成立,a=1,T=T+a=1,k=2,2<6,满足判断条件,继续循环;第二次:sin 0sin 12ππ=>=不成立,a=0,T=T+a=1,k=3,3<6,满足判断条件,继续循环;第三次:3sin1sin 02ππ=->=不成立,a=0,T=T+a=1,k=4,4<6, 满足判断条件,继续循环;第四次: 3sin 20sin 12ππ=>=-成立,a=1,T=T+a=2,k=5, 满足判断条件,继续循环;第五次:5sin 1sin 202ππ=>=成立,a=1,T=T+a=2,k=6,6<6不成立,不满足判断条件,跳出循环,故输出T的值3.题型四 复数的有关概念1.若复数()32z i i =-(i 是虚数单位),则z =( )A .23i -B .23i +C .32i +D .32i - 【答案】A【解析】∵23z i =+,所以23z i =-.2.设是虚数单位,表示复数的共轭复数。
(震撼推荐)2020届高三数学一轮复习必备系列精品(5算法初步)doc高中数学第五章算法初步考纲导读算法的含义、程序框图〔一〕了解算法的含义,了解算法的思想。
知识网络高考导航算法不仅是数学及其应用的重要组成部分,也是运算机科学的重要基础。
算法初步尽管是新课标增加的内容,但与前面的知识有着紧密的联系,同时与实际咨询题的联系也专门紧密。
因此,在高考中算法初步知识将与函数、数列、三角、概率、实际咨询题等知识点进行整合,是高考试题命制的新〝靓〞点。
如此试题就遵循了〝在知识网络交汇处设计试题〞的命制原那么,既符合高考命题〝能力立意〞的宗旨,又突出了数学的学科特点。
如此做,能够从学科的整体高度和思维价值的高度考虑咨询题,能够揭示数学各知识之间得到的内在联系,能够使考查达到必要的深度。
考查形式与特点是:〔1〕选择题、填空题要紧考查算法的含义、流程图、差不多算法语句等内容,一样在每份试卷中有1~2题,多为中档题显现。
(2)在解答题中可通过让学生读程序框图去解决其它咨询题,此类试题往往是与数列题结合在一起,具有一定的综合性,能够考查学生的识图能力及对数列知识的把握情形第1课时算法的含义基础过关1.算法的概念:对一类咨询题的机械的、统一的求解方法称为算法。
2.算法的特性:〔1〕有限性 〔2〕确定性例1.给出求1+2+3+4+5的一个算法。
解:算法1第一步:运算1+2,得到3第二步:将第一步中的运算结果3与3相加,得到6 第三步:将第二步中的运算结果6与4相加,得到10 第四步:将第三步中的运算结果10与5相加,得到15 算法2第一步:取n=5第二步:运算第三步:输出运算结果 变式训练1.写出求111123100++++的一个算法. 解:第一步:使1S =,; 第二步:使2I =;第三步:使1n I=; 第四步:使S S n =+; 第五步:使1I I =+;第六步:假如100I ≤,那么返回第三步,否那么输出S .例2. 给出一个判定点P ),(00y x 是否在直线y=x-1上的一个算法。
2020年高考数学二轮复习《算法初步、推理与证明、复数》综合测试卷注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数z 满足()1+21z =-i i ,则复数z 的虚部为( ) A .35B .35-C .35iD .35-i2.复数z 满足()234z +=-i i ,则z 在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限3.如果复数()2b b -∈R ii的实部和虚部互为相反数,那么b 等于( )A .2-B .CD .24.若复数z 满足22z =-i i (i 为虚数单位),则z 的共轭复数z 在复平面内对应的点所在的象限 是( ) A .第一象限B .第二象限C .第三象限D .第四象限5.执行如图所示的算法流程图,则输出的结果S 的值为( )A.-1 B.0 C.1 D.10096.执行如图所示的程序框图,输出s的值为()A.1008-C.1009 D.1007-B.10107.如图所示的程序框图输出的结果为30,则判断框内的条件是()A.5?n≤D.4?n<n<C.6?n≤B.5?8.我国古代著名的“物不知数”问题:“今有物其数大于八,二二数之剩一,三三数之剩一,五五数之剩二,问物几何?”即“已知大于八的数,被二除余一,被三除余一,被五除余二,问该数为多少?”为解决此问题,现有同学设计了如图所示的程序框图,则框图中的“”处应填入()A.16a-∈Z B.110a-∈Z C.210a-∈Z D.215a-∈Z9.“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是()A.201620172⨯B.201520182⨯C.201520172⨯D.201620182⨯10.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、丁的供词如下,甲说:“罪犯在乙、丙、丁三人之中”;乙说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一人是小偷”;丁说:乙说的是事实”.经过调查核实,四人中有两人说的是真话,另外两人说的是假话,且这四人中只有一人是罪犯,由此可判断罪犯是()A.甲B.乙C.丙D.丁11.一次猜奖游戏中,1,2,3,4四扇门里摆放了a,b,c,d四件奖品(每扇门里仅放一件).甲同学说:1号门里是b,3号门里是c;乙同学说:2号门里是b,3号门里是d;丙同学说:4号门里是b,2号门里是c;丁同学说:4号门里是a,3号门里是c.如果他们每人都猜对了一半,那么4号门里是() A .aB .bC .cD .d12.我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?” 意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( ) A .58 B .59 C .60 D .61二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.复数21=+ii__________. 14.设a ∈R ,若()()12a +-=-i i i ,则a =______ . 15.执行如图所示的程序框图,输出S 的值为___________.16.将正整数对作如下分组()()()()()()()()()()11122113223114233241,,,,,,,,,,,,,,,,则第100个数对为________________.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)已知复数()i 2iaz a =+∈+R . (1)若z ∈R ,求z ;(2)若z 在复平面内对应的点位于第一象限,求a 的取值范围.18.(12分)已知复数()()22lg 2232z m m m m =--+++i ,根据以下条件分别求实数m 的值或范围. (1)z 是纯虚数;(2)z 对应的点在复平面的第二象限.19.(12分)某函数的解析式由如图所示的程序框图给出.(1)写出该函数的解析式;(2)若执行该程序框图,输出的结果为9,求输入的实数x 的值.20.(12分)阅读如图所示的程序框图,解答下列问题:(1)求输入的x 的值分别为1-,2时,输出的()f x 的值;(2)根据程序框图,写出函数()()f x x ∈R 的解析式;并求当关于x 的方程()0f x k -=有三个互不相等的实数解时,实数k 的取值范围.21.(12分)下面()A ,()B ,()C ,()D 为四个平面图形:(1)数出每个平面图形的交点数、边数、区域数,并将下表补充完整;(2)观察表格,若记一个平面图形的交点数、边数、区域数分别为E ,F ,G ,试猜想E ,F ,G 之间的数量关系(不要求证明).22.(12分)(1)请用分析法证明:(2)已知a ,b 2.2020年高考数学二轮复习《算法初步、推理与证明、复数》综合测试卷答案一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】B【解析】因为()121z +=-i i ,所以()()1121131255z -----===+i i i i i ,因此复数z 的虚部为35-, 故选B . 2.【答案】D【解析】∵()2i 34i 5z +=-=,∴()()()2i 2i 52i z -+=-,()552i z =-,2i z =-,z 在复平面内对应的点()21-,,在第四象限,故选D . 3.【答案】A 【解析】∵复数()()()22=2b b b -⋅--=--⋅-i i i i i i i ,由题复数()2b b -∈R ii的实部和虚部互为相反数,∴2b =-.故选A .4.【答案】B【解析】由题意,∵()()()222222z -⋅--===--⋅-i i i i i i i ,∴22z =-+i ,则z 的共轭复数z 对应的点在第二象限.故选B . 5.【答案】B【解析】分由框图可知其所实现了求和232017cos cos cos ++cos2222S ππ++ππ=, 所以0S =,选B . 6.【答案】C【解析】执行程序框图: πS 01sin012=+⋅=+,3i =,32018>,否; 3πS 013sin0132=++⋅=+-,5i =,52018>,否; 5πS 0135sin01352=+-+⋅=+-+,7i =,72018>,否; …… 2017πS 0132017sin01320172=+-++⋅=+-++,2019i =,20192018>,是.输出()()()()S 013572015201701357920152017=+-+--+=++-++-+++-+1222150421009=++++=+⨯=.故选C .7.【答案】B【解析】当0S =,1n =时,不满足退出循环的条件,执行循环体后,2S =,2n =; 当2S =,2n =时,不满足退出循环的条件,执行循环体后,6S =,3n =; 当6S =,3n =时,不满足退出循环的条件,执行循环体后,14S =,4n =; 当14S =,4n =时,不满足退出循环的条件,执行循环体后,30S =,5n =; 当30S =,5n =时,满足退出循环的条件, 故判断框内的条件是5?n <,故选B . 8.【答案】A【解析】由题意,判断框内应该判断a 的值是否同时能被二除余一,被三除余一, 即判断16a -是否为整数.故选A . 9.【答案】B【解析】由题意,数表的每一行从右往左都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第2015行公差为20142, 故第1行的第一个数为:122-⨯,第2行的第一个数为:032⨯,第3行的第一个数为:142⨯,…第n 行的第一个数为:()212n n -+⨯, 表中最后一行仅有一个数,则这个数是201520182⨯.故选B . 10.【答案】B【解析】∵乙、丁两人的观点一致,∴乙、丁两人的供词应该是同真或同假;若乙、丁两人说的是真话,则甲、丙两人说的是假话,由乙说真话推出丙是罪犯的结论; 由甲说假话,推出乙、丙、丁三人不是罪犯的结论,矛盾; ∴乙、丁两人说的是假话,而甲、丙两人说的是真话; 由甲、丙的供述内容可以断定乙是罪犯.故选B . 11.【答案】A【解析】 由题意得,甲同学说:1号门里是b ,3号门里是c , 乙同学说:2号门里是b ,3号门里是d ; 丙同学说:4号门里是b ,2号门里是c ; 丁同学说:4号门里是a ,3号门里是c ,若他们每人猜对了一半,则可判断甲同学中1号门中是b 是正确的; 乙同学说的2号门中有d 是正确的;并同学说的3号门中有c 是正确的; 丁同学说的4号门中有a 是正确的,则可判断在1,2,3,4四扇门中,分别存有b ,d ,c ,a , 所以4号门里是a ,故选A . 12.【答案】C【解析】小女儿、二女儿和大女儿回娘家的天数分别是33,25,20,小女儿和二女儿、小女儿和大女儿、二女儿和大女儿回娘家的天数分别是8,6,5, 三个女儿同时回娘家的天数是1,所以有女儿在娘家的天数是:()332520865160++-+++=.故选C .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】1i +1i +. 14.【答案】1-【解析】()()()11+12a a a +-=+-=-i i i i ,10112a a a +=⇒=--=-⎧⎨⎩,故答案为1-. 15.【答案】48【解析】第1次运行,1i =,2S =,122S =⨯=,4i <成立, 第2次运行,2i =,2S =,224S =⨯=,4i <成立, 第3次运行,3i =,4S =,3412S =⨯=,4i <成立,第3次运行,4i =,12S =,41248S =⨯=,4i <不成立,故输出S 的值为48.16.【答案】()96, 【解析】根据题意,第一行有1个数对,数对中两个数的和为2,第二行有2个数对,数对中两个数的和为3,数对中第一个数由1变化到2,第二个数由2变化到1, 第三行有3个数对,数对中两个数的和为4,数对中第一个数由1变化到3,第二个数由3变化到1, 第四行有4个数对,数对中两个数的和为5,数对中第一个数由1变化到4,第二个数由4变化到1, ……第n 行有n 个数对,数对中两个数的和为1n +(),数对中第一个数由1变化到n ,第二个数由n 变化到1,前13行一共有1231391++++=个数,则第100个数对为第14行的第9个数,则第100个数对为()96,, 故答案为()96,.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)2z =;(2)05(,).【解析】(1若z ∈R ,则505a -=,所以5a =,2z =. (2)若在复平面内对应的点位于第一象限,则205a >且505a ->, 解得05a <<,即a 的取值范围为05(,). 18.【答案】(1)3m =;(2)133m +<<或-1<<1-3m .【解析】(1)由()()22lg 2232z m m m m =--+++i 是纯虚数得()22220320lg m m m m --=++≠⎧⎪⎨⎪⎩,即22221320m m m m --=++≠⎧⎪⎨⎪⎩,所以3m =.(2)根据题意得()22220320lg m m m m --<++>⎧⎪⎨⎪⎩,由此得220221320m m m m <--<++>⎧⎪⎨⎪⎩, 即133m +<<或-1<<1-3m .19.【答案】(1)2,121,1x x x y x -<⎧⎪=⎨+≥⎪⎩;(2)7x =-或3.【解析】(1)2,121,1x x x y x -<⎧⎪=⎨+≥⎪⎩.(2)当1x <时,29x -=,7x =-; 当1x ≥时,2+1=9x ,3x =,所以7x =-或3.20.【答案】(1)12,1;(2)()0,1.【解析】(1)当输入的x 的值为1-时,输出的()1122f x -==;当输入的x 的值为2时,输出的()222211f x =-⨯+=.(2)根据程序框图,可得()22,02,021,0x xf x x x x x ⎧<⎪==⎨⎪-+>⎩, 当0x <时,()2x f x =,此时()f x 单调递增,且()01f x <<; 当0x =时,()2f x =;当0x >时,()()22211f x x x x =-+=-在()0,1上单调递减, 在()1,+∞上单调递增,且()0f x ≥.结合图象,知当关于x 的方程()0f x k -=有三个互不相等的实数解时, 实数k 的取值范围为()0,1.21.【答案】(1)见解析;(2)1E G F +-=.【解析】(1)(2)观察表格,若记一个平面图形的交点数、边数、区域数分别为E ,F ,G ,4581+-=,58121+-=,2451+-=,, 可猜想E ,F ,G 之间的数量关系为1E G F +-=.22.【答案】(1)见解析;(2)见解析. 【解析】(1)要证5236+>+,只要证()()225236+>+,即证2018>,而上式显然成立,故原不等式成立.(2)假设结论不成立,则12a b +<,12b a+<, 所以114a b b a +++<,即11220a b a b ⎛⎫⎛⎫+-++-< ⎪ ⎪⎝⎭⎝⎭, 即22110a b a b ⎛⎫⎛⎫-+-< ⎪ ⎪⎝⎭⎝⎭,矛盾! 故假设不成立,所以1a b +与1b a+中至少有一个不小于2.。
专题11 算法初步1.【2019年高考天津卷理数】阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .29【答案】B【分析】根据程序框图,逐步写出运算结果即可.【解析】1,2S i ==;11,1225,3j S i ==+⨯==;8,4S i ==,结束循环,输出8S =.故选B .【名师点睛】解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 2.【2019年高考北京卷理数】执行如图所示的程序框图,输出的s 值为A .1B .2C .3D .4【答案】B【分析】根据程序框图中的条件逐次运算即可. 【解析】初始:1s =,1k =,运行第一次,2212312s ⨯==⨯-,2k =,运行第二次,2222322s ⨯==⨯-,3k =,运行第三次,2222322s ⨯==⨯-,结束循环,输出2s =,故选B .【名师点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.【2019年高考全国Ⅰ卷理数】如图是求112122++的程序框图,图中空白框中应填入A .12A A =+ B .12A A =+C .112A A=+D .112A A=+【答案】A【分析】本题主要考查算法中的程序框图,渗透阅读、分析与解决问题等素养,认真分析式子结构特征与程序框图结构,即可找出作出选择.【解析】初始:1,122A k ==≤,因为第一次应该计算1122+=12A +,1k k =+=2; 执行第2次,22k =≤,因为第二次应该计算112122++=12A +,1k k =+=3, 结束循环,故循环体为12A A=+,故选A .【秒杀速解】认真观察计算式子的结构特点,可知循环体为12A A=+.4.【2019年高考全国Ⅲ卷理数】执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于A .4122- B .5122-C .6122-D .7122-【答案】C【分析】根据程序框图,结合循环关系进行运算,可得结果. 【解析】输入的ε为0.01,11,01,0.01?2x s x ==+=<不满足条件; 1101,0.01?24s x =++=<不满足条件;⋅⋅⋅611101,0.00781250.01?22128S x =++++==<L 满足条件,结束循环;输出676111112(1)22222S =+++=⨯-=-L ,故选C .【名师点睛】解答本题关键是利用循环运算,根据计算精确度确定数据分析.5.【2019年高考江苏卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构;(2)要识别、运行程序框图,理解框图所解决的实际问题;(3)按照题目的要求完成解答并验证.6.【天津市和平区2018-2019学年度第二学期高三年级第三次质量调查】在如图所示的计算1592017++++L 的程序框图中,判断框内应填入的条件是A .2017?i ≤B .2017?i <C .2013?i <D .2021?i ≤【解析】由题意结合流程图可知当2017i =时,程序应执行S S i =+,42021i i =+=, 再次进入判断框时应该跳出循环,输出S 的值;结合所给的选项可知判断框内应填入的条件是2017?i ≤.故选A .7.【吉林省长春市北京师范大学长春市附属中学2019届高三第四次模拟考试】根据如图所示的程序框图,当输入的x 值为3时,输出的y 值等于A .1B .eC .1e -D .2e -【答案】C【解析】由题3x =,231x x =-=-,此时0x >,继续运行,1210x =-=-<,程序运行结束,得1e y -=,故选C .8.【西南名校联盟重庆市第八中学2019届高三5月高考适应性月考卷(六)】执行如图所示的程序框图,则输出的值为A .4B .5C .6D .7【解析】由题可得3,27,315,431,563,6S i S i S i S i S i ==→==→==→==→==, 此时结束循环,输出6i =,故选C .9.【山东省济宁市2019届高三二模】阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于A .30B .31C .62D .63【答案】B【解析】由流程图可知该算法的功能为计算123412222S =++++的值,即输出的值为512341(12)122223112S ⨯-=++++==-.故选B .10.【辽宁省大连市2019届高三第二次模拟考试】执行如图所示的程序框图,若输出结果为1,则可输入的实数x 值的个数为A .1B .2C .3D .4【分析】根据程序框图的含义,得到分段函数221,2log ,2x x y x x ⎧-≤⎪=⎨>⎪⎩,分段解出关于x 的方程,即可得到可输入的实数x 值的个数.【解析】根据题意,该框图的含义是:当2x ≤时,得到函数21y x =-;当2x >时,得到函数2log y x =, 因此,若输出的结果为1时,若2x ≤,得到211x -=,解得2x = 若2x >,得到2log 1x =,无解,因此,可输入的实数x 的值可能为2-2,共有2个.故选B . 11.【江西省新八校2019届高三第二次联考】如图所示的程序框图所实现的功能是A .输入a 的值,计算2021(1)31a -⨯+的值B .输入a 的值,计算2020(1)31a -⨯+的值C .输入a 的值,计算2019(1)31a -⨯+的值D .输入a 的值,计算2018(1)31a -⨯+的值 【答案】B【解析】由程序框图,可知1a a =,132n n a a +=-,由i 的初值为1,末值为2019,可知,此递推公式共执行了201912020+=次,又由132n n a a +=-,得113(1)n n a a +-=-,得11(1)3n n a a --=-⨯即1(1)31n n a a -=-⨯+,故2021120202021(1)31(1)31a a a -=-⨯+=-⨯+,故选B . 12.【山西省2019届高三考前适应性训练(二模)】执行如图所示的程序框图,则输出x 的值为A .2-B .13-C .12D .3【答案】A【分析】根据程序框图进行模拟运算得到x 的值具备周期性,利用周期性的性质进行求解即可.【解析】∵12x =,∴当1i =时,13x =-;2i =时,2x =-; 3i =时,3x =,4i =时,12x =,即x 的值周期性出现,周期数为4,∵201850442=⨯+,则输出x 的值为2-,故选A .【名师点睛】本题主要考查程序框图的识别和判断,结合条件判断x 的值具备周期性是解决本题的关键,属于中档题.13.【青海省西宁市第四高级中学、第五中学、第十四中学三校2019届高三4月联考】若某程序框图如图所示,则该程序运行后输出的值是A .5B .4C .3D .2【答案】B【分析】模拟执行循环结构的程序得到n 与i 的值,计算得到2n =时满足判断框的条件,退出循环,输出结果,即可得到答案.【解析】模拟执行循环结构的程序框图, 可得:6,1n i ==, 第1次循环:3,2n i ==; 第2次循环:4,3n i ==; 第3次循环:2,4n i ==,此时满足判断框的条件,输出4i =.故选B .【名师点睛】本题主要考查了循环结构的程序框图的应用,其中解答中根据给定的程序框图,根据判断框的条件推出循环,逐项准确计算输出结果是解答的关键,着重考查了考生的运算与求解能力,属于基础题.14.【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第三次调研】下图是一个算法流程图.若输出y 的值为4,则输入x 的值为______________.【答案】1-【解析】当1x ≤时,由流程图得3y x =-, 令34y x =-=,解得1x =-,满足题意. 当1x >时,由流程图得3y x =+, 令34y x =+=,解得1x =,不满足题意. 故输入x 的值为1-.15.【北京市人大附中2019届高三高考信息卷(三)】执行如图所示的程序框图,若输入x 值满足24x -<≤,则输出y 值的取值范围是______________.【答案】[3,2]-【解析】根据输入x 值满足24x -<≤,利用函数的定义域,分成两部分:即22x <<﹣和24x ≤≤,当22x <<﹣时,执行23y x =- 的关系式,故31y -≤<, 当24x ≤≤时,执行2log y x =的关系式,故12y ≤≤. 综上所述:[3,2]y ∈-,故输出y 值的取值范围是[3,2]-.。
专题十二算法初步挖命题【真题典例】(2O18M标II, 7. 5分丨期| 2.亠+*+十诘_|牯, 間卜r卜硝的秤序柄图,则在空白HT;应垃人❶核心考点i辭序框i礼畫算痣的W1W 构及框帽表灵❷思路分析模别怦序框图的运行过程如a濯序运斤后♦樹L的由此和空H框瓯頊人的箫件. ❸解答过程答案:BFI ;■ ] 4…心】爲心I* +朴■ ■+缶HT++*■+侖L芍不满埜*'J I茁班内旳蓬件时.5=^-7.所UV lt^-+ 斗朴"+箱y.7"=土+£*…*箱『诉【=空t l{H❹温馨提示弼劇綃环誥車的爺件的关健昌弄睛循环是出型犢耳悄梅还是恵询现^■<-."1 ,.两冲细抱的陋成抽材胡环体的执厅歇数是1-1 的•卄敵变圧和祟棘象F变慑一魅是同申执打的.眾加(乘1—次.计救一次.❺易错分析睦不懂程序曲的功眦畀不湖tt押1FA什么.是出错的主鑿牌一连盍JLt常用堂总:Hiif fcii-d.如E+i;内洋加宅用"虹;=S十齢冃屠宰它咼・姻厂户沫@方法归纳补全程申軽圉的F崔:⑷骰故卷败拥足判慚卷件.抖行循环体;㈢运疔循玮皓构.直別込的杲勺題H昱蚀输州葯审郴岡勿止1仙IH据此时备屮童酬的值■补余稈序I桥溉❼命题规律|必考内容:苇査睛环结恂的程序惬图・程序框同的功SL朮林榊的输心M.值,补全程序蘇.2等査形灵土以选择题为主,偶尔UU1#惶題也成出現工分值:s分❽能力要求I m*怯的會JU Tftx^MUi.的「韩基朕邂報结构:W结M.為件皓构、箱”詰构,1【考情探究】查考生的数学运算能力和逻辑推理能力破考点 【考点集训】考点程序框图与算法语句1.(2016课标川,7,5分)执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=()考点内容解读5年考情预测热度考题示例考向关联考点程序框 图与算 法语句① 了解算法的含义和思想. ② 理解程序框图的二种基 本逻辑结构:顺序结构、条 件结构、循环结构•③ 理解几种基本算法语句输入语句、输出语句、 赋值语句、条件语句、循环 语句的含义2018课标n ,7,5 分补全程序框图 数列 ★★★2017课标1,8,5 分 补全程序框图指数运算2016课标1,9,5 分 2015课标1,9,5 分 2014课标1,7,5 分求循环结构 的输出值2017课标川,7,5 分 求循环结构的输入值2015课标n ,8,5 分 条件结构的程序框图更相减损术分析解读从近五年的考查情况来看,本专题内容一般以选择题、填空题的形式出现,分值为5分,难度中A.3B.4C.5D.6等偏下•主要的命题角度有条件结构与分段函数相结合,求循环结构的输入值、输出值补全程序框图等•考答案 B2.(2017安徽黄山二模,6)已知x 的取值范围是[0,8],执行如图所示的程序框图,则输出的答案 B 3.(2018河南开封一模,8)我国古代名著《庄子 天下篇》中有一句名言 一尺之棰,日取其半,万世不竭”,其意思:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如 图所示的程序框图的功能就是计算截取 7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的语句是(答案 D炼技法 【方法集训】方法1程序框图求解方法A. -B. 一C.一D.-A.i<7,s=s- -,i=2i C.i<7,s= -,i=i+1 D.i W7,s= -,i=i+1B.i1. (2018广东汕头一模,7)执行如图所示的程序框图,输出的结果是()2.(2018山东济南一模,10)执行如图所示的程序框图,当输入i=2 018时,输出的结果为答案 B方法2 补全程序框图的方法1.(2018湖南(长郡中学、衡阳八中)、江西(南昌二中)等十四校第二次联考,8)如图是为了A.56 答案 BB.54C.36D.64A.-1 008B.1 009C.3 025D.3 028求出满足21+22+・・+2n>2 018的最小整数和 _________________ 两个空白框中,可以分别填入()A. i<30, n=n+2C.i>30 ,n=n+ 2 答案CB. i=30 ,n=n+2D.i>30 ,n=n+1过专题【五年高考】A组统一命题课标卷题组A. S>2 018?;输出n-1B. S>2 018?;输出nC. S€018?;输出n-1D. S€018?;输出n答案A2.(2017广东惠州第二次调研填入的是(),8)如图是计算・、+・+••+_的值的程序框图,其中①②处应分别*S=0JF=2J=1r^~ii心11i” * ”〔心〕1.(2017课标I ,8,5分)下面程序框图是为了求出满足3n -2n >1 000的最小偶数n,那么在.和一两个空白框中,可以分别填入()答案 DA. A>1 000 和 n=n+1B. A>1 000 和 n=n+2C. A W 000 和 n=n+1D. A <1 000 和 n=n+22.(2016 课标 I ,9,5分)执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y 的值满A. y =2xB. y=3x C. y =4xD. y =5x答案 C3.(2015 课标 n ,8,5分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的A.0B.2C.4D.14更相减损术”.执行该程序框图a=()答案 B4.(2014课标I ,7,5分)执行下面的程序框图,若输入的a,b,k 分别为1,2,3,则输出的M=()答案 DB 组自主命题省(区、市)卷题组答案 B 2.(2018天津,3,5分)阅读下边的程序框图,运行相应的程序,若输入N 的值为20,则输出TA.—B.-C.—D.—1.(2018 北京,3,5分)执行如图所示的程序框图,输出的s 值为(A.—B.-C.-D.— /叭/的值为()A.1B.2C.3答案B3. (2017山东,6,5分)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输D.4入的x的值为9,则第一次、第二次输出的a的值分别为(A.0,0B.1,1C. 0,1D.1,0答案D4. (2017 江苏,4,5 分)下图是一个算法流程图.若输入x的值为一,则输出y的值/输山/C 组教师专用题组3.(2017北京,3,5分)执行如图所示的程序框图,输出的s 值为()答案 -2 1.(2017 最小值为课标,7,5分)执行下面的程序框图,为使输出S 的值小于91,则输入的正整数 N 的A.5 答案 D2.(2017 的值为(B.4C.3天津,3,5分)阅读下面的程序框图,运行相应的程序,若输入N 的值为24,则输出N )A.0 答案 CB.1C.2答案 C 4.(2016四川,6,5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法 ,至今仍是比较先进的算法.如图所示的程 序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x 的值分别为3,2,则输出v 的值为()答案 BA.2B.-C.- A.9 B.18 C.20D._D.355.(2016 北京,3,5,若输入的a值为1,则输出的k值为(分)执行如图所示的程序框图A.1B.2C.3D.4答案 B6.(2016天津,4,5分)阅读下边的程序框图,运行相应的程序,则输出S 的值为()答案 CA.2B.4 答案 BC.67.(2015 课标 I ,9,5 A.5 B.6 分)执行下面的程序框图,如果输入的C.7D.88.(2015湖南,3,5分)执行如图所示的程序框图.如果输入n=3,则输出的S=()答案 C10.(2015重庆,7,5分)执行如图所示的程序框图,若输出k 的值为 件是()A.—B.-C.- 答案 B 9.(2015 福建,6,5 A.2B.1 D.-分)阅读如图所示的程序框图 ,运行相应的程序C.0D.-1则输出的结果为()A.s wB.s wC.s wD.s w8,则判断框内可填入的条北京,3,5分)执行如图所示的程序框图,输出的结果为( )13.(2014课标II ,7,5分)执行下面的程序框图,如果输入的x,t 均为2,则输出的S=( )答案 C11.(2015 A.(-2,2) C.(-4,-4) 答案 B12. (2015 B.(-4,0) D. (0,-8)天津,3,5分)阅读下边的程序框图,运行相应的程序,则输出S 的值为(A.-10 答案 BB.6C.14D.18的i 的值为 _________答案 315. __________________________________________________________ (2015山东,13,5分)执行下边的程序框图,输出的T 的值为 _________________________________答案 一A.4B.5 答案 DC.6 CO DD.714. (2016山东,11,5分)执行如图所示的程序框,若输入的a,b 的值分别为0和9,则输出[n 跟|/ w 人心/【三年模拟】选择题(每小题5分,共45分)1.(2019届全国I卷高三五省优创名校联考值为大于1 000的最小数值,则在空白的判断框内可以填入的是答案B1. (2019届陕西四校联考,8)执行如图所示的程序框图,输出的S=(I __[开始]A.25B.9C.17D.20答案C2. (2019届四川攀枝花高三第一次统考,6)运行如图所示的程序框图()A.i<6B.i<7C.i<8D.i<9A.-—B.0C.一D. ,则输出的结果S为$■1、m21.(2019届全国I卷高三五省优创名校联考。
1.算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.2.程序框图程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.3.三种基本逻辑结构突破点一 程序框图的输入、输出问题例1 1、执行如图所示的程序框图,输出的s 值为_____56___.2、执行如图所示的程序框图,则输出S 的值为( D )A .-32 B.32 C .-12 D.123、执行如图所示的程序框图,则输出的S =____940____.4、执行如图所示的程序框图,如果输出的k 的值为3,则输入的a 的值可以是( A )A.20 B.21 C.22 D.235、我国古代数学著作《骨髀算经》有如下问题:“今有器中米,不知其数.前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k的值为(B)A.4.5 B.6 C.7.5 D.9突破点二程序框图的补全问题例2 1、执行如图所示的程序框图,若输出S的值为-20,则条件框内可填写(D)A .i >3?B .i <4?C .i >4?D .i <5?解析:选D 初始值:i =1,S =10; 第一次循环:S =10-21=8,i =2; 第二次循环:S =8-22=4,i =3; 第三次循环:S =4-23=-4,i =4;第四次循环:S =-4-24=-20,i =5. 因为输出S 的值为-20,所以条件框内可填“i <5?”. 2、执行如图所示的程序框图,若输出的值为21,则判断框内可填( )A .n ≥5?B .n >6?C .n >5?D .n <6?解析:选B 初始值:n =0,S =0; 第一次循环:n =1,S =1; 第二次循环:n =2,S =1+2=3; 第三次循环:n =3,S =3+3=6; 第四次循环:n =4,S =6+4=10;第五次循环:n =5,S =10+5=15; 第六次循环:n =6,S =15+6=21; 第七次循环:n =7. 因为输出的值为21,所以结合选项可知判断框内可填“n >6?”,故选B.3、执行如图所示的程序框图,若输入m =1,n =3,输出的x =1.75,则空白判断框内应填的条件为( B )A .|m -n |<1?B .|m -n |<0.5?C .|m -n |<0.2?D .|m -n |<0.1?解析::输入m =1,n =3. 第一次执行,x =2,22-3>0,n =2,返回;第二次执行,x =32,⎝⎛⎭⎫322-3<0,m =32,返回; 第三次执行,x =3+44=74,⎝⎛⎭⎫742-3>0,n =74.输出x =1.75,故第三次执行后应满足判断框,此时m -n =32-74=-14,故选B.4、(2018·全国卷Ⅱ)为计算S =1-12+13-14+…+199-1100,设计了如图所示的程序框图,则在空白框中应填入( B )A .i =i +1B .i =i +2C .i =i +3D .i =i +4[解析] (1)由题意可将S 变形为S =⎝⎛⎭⎫1+13+…+199-⎝⎛⎭⎫12+14+…+1100,则由S =N -T ,得N =1+13+…+199,T =12+14+…+1100.据此,结合N =N +1i ,T =T +1i +1易知在空白框中应填入i =i +2.故选B. 突破点二 辨析程序框图的功能例3如图所示的程序框图,该算法的功能是( C )A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值D.计算[1+2+3+…+(n-1)]2+(20+21+22+…+2n)的值1、(2016·全国卷Ⅰ)执行如图的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足(C)A.y=2x B.y=3x C.y=4x D.y=5x2、(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入(D)A.A>1 000?和n=n+1 B.A>1 000?和n=n+2C.A≤1 000?和n=n+1 D.A≤1 000?和n=n+23、(2017·全国卷Ⅱ)执行如图所示的程序框图,如果输入的a=-1,则输出的S=(B)A.2 B.3 C.4 D.5解析:B[当K=1时,S=0+(-1)×1=-1,a=1,执行K=K+1后,K=2;当K=2时,S=-1+1×2=1,a=-1,执行K=K+1后,K=3;当K=3时,S=1+(-1)×3=-2,a=1,执行K=K+1后,K=4;当K=4时,S=-2+1×4=2,a=-1,执行K=K+1后,K=5;当K=5时,S=2+(-1)×5=-3,a=1,执行K=K+1后,K=6;当K=6时,S=-3+1×6=3,执行K=K+1后,K=7>6,输出S=3.结束循环.故选B.]4、(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如是图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=(C)A.7 B.12 C.17 D.34解析:C[输入x=2,n=2.第一次,a=2,s=2,k=1,不满足k>n;第二次,a=2,s=2×2+2=6,k =2,不满足k>n;第三次,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17.]5、如图所示的程序框图,其作用是输入x 的值,输出相应的y 值,若x =y ,则这样的x 的值有( C )A .1个B .2个C .3个D .4个解析:C [当x ≤2时,令y =x 2=x ⇒x (x -1)=0,解得x =0或x =1;当2<x ≤5时,令y =2x -4=x ⇒x =4;当x >5时,令y =1x=x ,无解.综上可得,这样的x 的值有3个.]6、如图是计算1+13+15+…+131的值的程序框图,则图中①②处应填写的语句分别是( A )A .n =n +2,i >16?B .n =n +2,i ≥16?C .n =n +1,i >16?D .n =n +1,i ≥16?7、“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前.如图所示的程序框图的算法思路就是来源于“欧几里得算法”,执行该程序框图(图中“a MOD b ”表示a 除以b 的余数),若输入的a ,b 分别为675,125,则输出的a =( )A .0B .25C .50D .75解析:选B初始值a=675,b=125.第一次循环c=50,a=125,b=50;第二次循环c=25,a=50,b=25;第三次循环c=0,a=25,b=0,此时不满足循环条件,退出循环,输出a的值为25,故选B.8、执行如图所示的程序框图,若输入的t=4,则输出的i=()A.7 B.10 C.13 D.16解析:选D输入t=4,i=1,S=0,S<4,i=1不是质数,S=0-1=-1,i=4,S<4;i=4不是质数,S=-1-4=-5,i=7,S<4;i=7是质数,S=-5+7=2,i=10,S<4;i=10不是质数,S=2-10=-8,i=13,S<4;i=13是质数,S=-8+13=5,i=16,S>4,退出循环,故输出的i=16.故选D.9、某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图中记录了每天的销售量(单位:台),把这些数据经过如图所示的程序框图处理后,输出的S=()A.28 B.29 C.196 D.203解析:选B由程序框图可知,该程序框图输出的是销售量的平均值,结合茎叶图可知,输出的S=20+22+26+33+33+34+357=29,故选B.10、执行如图所示的程序框图,若输出的s=25,则判断框中可填入的条件是()A.i≤4? B.i≥4? C.i≤5? D.i≥5?解析:选C执行程序框图,i=1,s=100-5=95;i=2,s=95-10=85;i=3,s=85-15=70;i =4,s=70-20=50;i=5,s=50-25=25;i=6,退出循环.此时输出的s=25.结合选项知,选C.11、我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:“今有出门望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?”现在我们用如图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是()A.S>10 000? B.S<10 000?C.n≥5? D.n≤6?解析:选B根据题意,利用程序框图求禽的数目,输出结果应为S=9×9×9×9×9=59 049.循环共执行了5次,所以判断框中应填入的条件是“S<10000?”或“n≤5?”或“n<6?”.故选B.12、图(1)是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( D )A.7 B.8 C.9 D.10解析:D[从算法流程图可知,该图是统计成绩大于或等于90分的考试次数.从茎叶图可知输出的结果为10.] 13、如图,如图算法框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1 000,输出的结果为788,则运用此方法估计的π的近似值为________(保留四位有效数字).解析:根据算法框图知,如果点在圆x2+y2=1内,m就增加1;现输入N=1 000,m起始值为0,输出结果为788,说明m增加了788次,也就是说有788个点在圆x2+y2=1内.设圆的面积为S1,正方形的面积为S2,则概率p=7881 000≈S1S2=π4,∴π≈4p=4×0.788=3.152.答案:3.152。