讲义-高分辨电镜20130812
- 格式:doc
- 大小:12.31 MB
- 文档页数:26








第六部分高分辨电镜的成像原理及在材料科学中应用6.1 高分辨电镜图像的类型通过高分辨电镜得到的图像通常称为晶格像,这些图像中可以带给研究者的信息大不相同,主要是由于成像条件不同,以及样品厚度不同。
了解这些影响因素才有利于研究者控制成像条件,获取研究所需要的有用信息。
高分辨电镜图像可分为:晶格条纹;一维结构图像;二维晶格条纹;二维结构图像。
1)晶格条纹(lattice fringes)晶格条纹像的成像条件没有严格限制,只要有两列电子波干涉成像即可,不要求对准晶带轴,在很宽的离焦条件和不同样品厚度下都可以观察到,所以很容易获得。
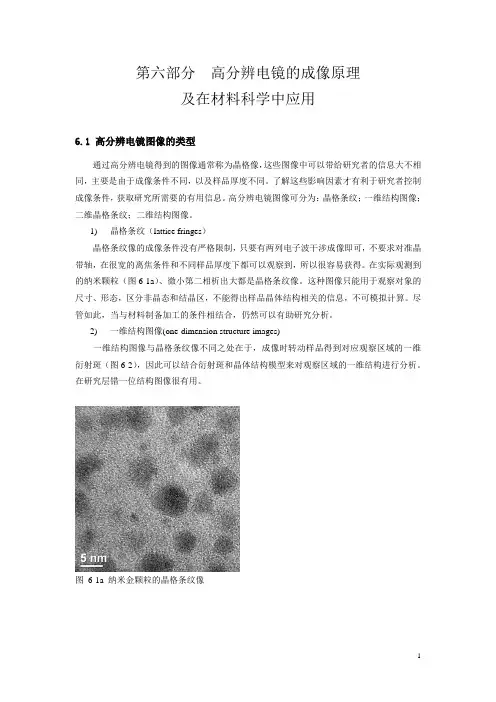
在实际观测到的纳米颗粒(图6-1a)、微小第二相析出大都是晶格条纹像。
这种图像只能用于观察对象的尺寸、形态,区分非晶态和结晶区,不能得出样品晶体结构相关的信息,不可模拟计算。
尽管如此,当与材料制备加工的条件相结合,仍然可以有助研究分析。
2)一维结构图像(one-dimension structure images)一维结构图像与晶格条纹像不同之处在于,成像时转动样品得到对应观察区域的一维衍射斑(图6-2),因此可以结合衍射斑和晶体结构模型来对观察区域的一维结构进行分析。
在研究层错一位结构图像很有用。
图6-1a 纳米金颗粒的晶格条纹像图6-2 一维结构图像3)二维晶格像(two-dimensional lattice image)大部分文献中出现的都是二维晶格像,此时晶体的某一晶带轴平行于入射电子束,因此相应的衍射花样对应晶胞的衍射谱。
在不同的欠焦量下和样品厚度均可以获得二维晶格像,这是其大量出现的原因,也被广泛用于材料科学的研究中,用于获得位错、晶界、相界、析出、结晶等信息。
要注意的是二维晶格像的花样是随着欠焦量、样品厚度以及光阑尺寸改变的,不能简单指定原子的位置。
在不确定的成像条件下不能得到晶体的结构信息,可以计算模拟辅助分析。
4)二维结构图像(two-dimension structure images)二维结构图像是严格控制条件下的二维晶格像,首先样品要很薄(小于10 nm),避免多次散射的不利影响;其次要使晶体的晶带轴严格平行于入射电子束;成像时欠焦量是控制(已知)的,通常最佳欠焦条件(Scherzer focus)下的图像衬度最大。


金属晶体的高分辨电镜图像金属晶体的高分辨电镜图像金属晶体是由金属原子按照一定的几何排列方式组成的晶体结构。
高分辨电镜是一种用于观察材料微观结构的仪器,它能够提供高分辨率的图像,显示出晶体的细节和原子的位置。
下面是根据金属晶体的高分辨电镜图像所进行的步骤思考。
第一步,观察晶体的整体形状和外貌。
首先,我会仔细观察晶体的外观,如是否呈现出规则的几何形状,是否存在明显的表面和边界。
通过这些观察,我可以初步了解晶体的形貌和尺寸。
第二步,分析晶体的晶格结构。
在电镜图像中,我会关注晶体的晶格结构,即原子的排列方式。
通过观察图像中的晶格点和晶格面,我可以确定晶体的晶格类型,如立方晶格、六方晶格等。
第三步,观察晶体的晶面和晶界。
在高分辨电镜图像中,我会特别注意晶体中的晶面和晶界。
晶面是晶体内部的平坦面,而晶界是两个晶体颗粒的交界处。
通过观察晶面的形状和晶界的结构,我可以推断出晶体的生长过程和可能存在的晶界缺陷。
第四步,测量晶体的晶格常数。
利用高分辨电镜图像,我可以测量晶体的晶格常数,即晶格中相邻原子之间的距离。
通过测量晶格常数,我可以确定晶体的晶胞参数,从而进一步了解晶体的结构和性质。
第五步,研究晶体的晶体缺陷。
在高分辨电镜图像中,我会寻找晶体中的缺陷,如位错、空位和间隙等。
这些缺陷可以对晶体的力学性能和电学性能产生重要影响。
通过研究晶体缺陷,我可以进一步理解晶体的生长和变形机制。
总之,金属晶体的高分辨电镜图像提供了观察晶体微观结构的重要途径。
通过仔细观察和分析电镜图像,我们可以了解晶体的形貌、晶格结构、晶面和晶界、晶格常数以及晶体缺陷等信息。
这些信息对于理解晶体的性质和行为具有重要意义,也为材料科学和工程提供了重要的参考依据。
第六部分高分辨电镜的成像原理及在材料科学中应用6.1 高分辨电镜图像的类型通过高分辨电镜得到的图像通常称为晶格像,这些图像中可以带给研究者的信息大不相同,主要是由于成像条件不同,以及样品厚度不同。
了解这些影响因素才有利于研究者控制成像条件,获取研究所需要的有用信息。
高分辨电镜图像可分为:晶格条纹;一维结构图像;二维晶格条纹;二维结构图像。
1)晶格条纹(lattice fringes)晶格条纹像的成像条件没有严格限制,只要有两列电子波干涉成像即可,不要求对准晶带轴,在很宽的离焦条件和不同样品厚度下都可以观察到,所以很容易获得。
在实际观测到的纳米颗粒(图6-1a)、微小第二相析出大都是晶格条纹像。
这种图像只能用于观察对象的尺寸、形态,区分非晶态和结晶区,不能得出样品晶体结构相关的信息,不可模拟计算。
尽管如此,当与材料制备加工的条件相结合,仍然可以有助研究分析。
2)一维结构图像(one-dimension structure images)一维结构图像与晶格条纹像不同之处在于,成像时转动样品得到对应观察区域的一维衍射斑(图6-2),因此可以结合衍射斑和晶体结构模型来对观察区域的一维结构进行分析。
在研究层错一位结构图像很有用。
图6-1a 纳米金颗粒的晶格条纹像图6-2 一维结构图像3)二维晶格像(two-dimensional lattice image)大部分文献中出现的都是二维晶格像,此时晶体的某一晶带轴平行于入射电子束,因此相应的衍射花样对应晶胞的衍射谱。
在不同的欠焦量下和样品厚度均可以获得二维晶格像,这是其大量出现的原因,也被广泛用于材料科学的研究中,用于获得位错、晶界、相界、析出、结晶等信息。
要注意的是二维晶格像的花样是随着欠焦量、样品厚度以及光阑尺寸改变的,不能简单指定原子的位置。
在不确定的成像条件下不能得到晶体的结构信息,可以计算模拟辅助分析。
4)二维结构图像(two-dimension structure images)二维结构图像是严格控制条件下的二维晶格像,首先样品要很薄(小于10 nm),避免多次散射的不利影响;其次要使晶体的晶带轴严格平行于入射电子束;成像时欠焦量是控制(已知)的,通常最佳欠焦条件(Scherzer focus)下的图像衬度最大。
尽管如此,晶体结构和原子位置并不能简单从图像上“看到”,欠焦量和样品厚度依然控制着晶格相的亮暗分布。
需要采用计算机辅助的图像模拟分析技术,才可能确定晶体结构以及原子位置。
图6-3 二维晶格像6.2 高分辨电镜的成像过程6.2.1 基本过程描述在透射电镜中入射电子束(incident beam)穿过样品,当样品为晶体时,在物镜背焦面(back focal plane)上会得到电子衍射花样,这是电子束受到样品晶格散射的结果,每个晶面的散射斑点可以用布拉格公式(Bragg condition)来确定,在与入射束成2θ的方位得到该晶面的散射斑hkl。
于是我们在物镜背焦面上得到一系列的电子束子波,这些电子波在后续的传播过程中重新干涉叠加,在像平面上得到于对应物体的图像。
我们可以用位于物镜背焦面上的物镜光阑(objective aperture)来选取用来成像的电子束,从而达到控制成像的目的。
例如当我们只选取透射束成像,得到明场像(bright field image);而当我们选取一个特定衍射束成像时,就得到了暗场像(dark fild image)。
在以往的电镜操作中,成像过程造成电子束强度的显著差别,即电子波振幅的大幅度变化,因此得到图像的衍射衬度是振幅衬度(amplitude contrast)。
如果我们选取透射束和一个衍射束成像时,这两个电子束干涉叠加,就会在像平面得到规律的干涉图像。
因为这个衬度来自透射束和衍射束的相位差,因此称为相位衬度(phasecontrast )。
假设这两个电子波之间存在特定的相位差,有相同的传播方向,电子束干涉叠加就会发生。
当电镜的分辨能力很高,足以分辨出干涉条纹的明暗分布时,我们就得到了高分辨图像,也就是晶格条纹像,这个干涉图像与样品的原子排列有关。
示意图6-4中显示了电子显微镜的成像过程。
高分辨成像过程要用电子的波动性质来描述,因此称为入射电子波,穿过样品的电子波称为样品出射波。
在穿透过程中样品对入射电子波进行调制(即改变波的振幅、位相),导致样品出射波函数中携带了样品原子排列信息。
请注意 我们得到的是原子排列,也就是晶体、晶胞的信息,而不是原子本身的信息。
样品出射波经过物镜系统传递到像平面上,得到高分辨像。
采用“传递”来描述成像过程的处理是为了数学上的方便,成像过程可以表达成“传递函数”求解,因而样品出射波函数经过传递函数处理后就得到像函数。
图 6-4 透射电镜的成像过程6.2.2 晶格条纹像的形成过程当只有透射束和一个强衍射束参加成像时,两电子束干涉得到一维条纹像。
操作中可以用物镜光阑在背焦面上来选择所需的成像电子束。
图7-5后焦面 样品 像平面电子源物镜图 6-5一维晶格条纹像的形成过程示意图晶格条纹间距d tm 与衍射晶面的倒易矢量存在如下关系:(注意每个量都是矢量) 当有透射束和两个以上强衍射束参加成像时,多个电子束干涉得到二维晶格像(图6-6),这就是我们最常见到的高分辨图像的形式。
图 6-6 二维晶格像形成过程示意图6.3 高分辨成像分析中的几个概念6.3.1 空间频率 (spatial frequency)我们看到,入射电子波在穿过晶体样品时被散射到不同的角度。
将不同的散射角定义成空间频率,沿光轴中心为低频率通道,大角度散射为高频率通道。
这样做的原因是不同频率的电子波在穿过透射电镜成像时的光波传递效果不一样,从而对图像质量的贡献不同,下面我们将会仔细分析。
从布拉格定律可知散射角度与晶面间距成反比。
晶体样品可以看作光栅,其晶面间距的倒数(d -1)就可以看作空间频率。
因为电镜成像的样品是薄膜,通常空间频I1211g g g d tm tm -==率是二维的。
6.3.2 Moiré像这是一个广泛存在的现象。
当不同周期和取向的条纹交叠在一起时,就会出现干涉条纹。
干涉的出现放大了原来的条纹间距,满足关系注意干涉条纹的方向可能完全不同于原来条纹的方向,如图6-7(b)中当两个条纹有一定夹角时的情况,此时三者之间仍然满足矢量关系。
Moiré像的成像原理和图像特征与高分辨电镜中的一维晶格像非常相似,但条纹间距比较大,见图6-8。
图 6-7 Moiré干涉条纹的形成1211g g g d tm tm -==图6-8 Moiré干涉条纹的实例6.3.3 傅里叶变换(Fourier transform, 简称FT变换)样品出射波经过物镜成像后,在物镜背焦面上得到一组衍射斑点。
样品对入射波的作用过程在数学上可以用傅里叶变换来描述,这是将正空间(real space)的波函数变换为倒易空间(reciprocal space)的操作,透镜作用是将一组组平行衍射电子束会聚在透镜后焦面上。
而衍射斑点干涉叠加得到图像的过程刚好反过来,是一个反傅里叶变换(FT-1),又转换为图像的正空间。
关于傅里叶变换的数学原理和操作方法可以在数学书籍中查到,现在的成像控制软件和图像分析软件中都有傅里叶变换功能,帮助我们在衍射斑和图像之间轻松进行转换。
例如图6-9中,利用傅里叶变换我们可以将晶格像转换得到相应的一组衍射斑点,对其晶体结构进行分析。
图6-9晶格像经傅里叶变换得到相应衍射斑点6.3.4 弱相位物体 (weak-phase object)当样品很薄(小于10 nm ,通常小于5 nm )时吸收可以忽略,此时衍射电子波的振幅几乎与入射电子波相等,而衍射电子波的相位会有一个改变,这个变化正比于样品厚度。
因此出射波函数可以写成△Z 是样品厚度,σ是交互作用常数,与加速电压和样品原子序数有一定关系,200kV 电压下的取值是0.00729V -1nm -1。
φ(x,y)是样品的晶体势场沿电子束入射方向的分布,当样品厚度仅为几个纳米时,对波的相位改变很小,σφ(x,y)Δz 远小于1,因此可以用线性化处理:())),(ex p(,z y x i y x exit ∆=ψσϕ()z y x i y x exit ∆+=ψ),(1,σϕ此时不仅是数学计算的方便,晶格像与样品原子排列之间也会有更直接的对应关系。
因此很薄的样品被称为弱相位物体。
低原子系数组成的样品和高于200kV的电压将有利于保持弱相位物体近似成立。
对于厚样品,由于多重散射和散射电子束之间的交互作用,以上关系不再成立。
(厚度大于10nm的样品中采用Bloch波来计算出射波,并采用多层片法快速得到计算结果。
)6.3.5 阿贝成像原理电镜成像可以用阿贝成像原理描述,其要点为:1)样品射出波为不同空间频率的子波;2)各个子波在成像系统(物镜)中独立传播;3)透镜对各子波传递质量不同;4)图像质量取决于收集到的子波数量,以及透镜对各子波传递质量。
阿贝成像原理是物理光学的一个理论,最初应用在可见光的传播成像。
主要贡献是解释了近轴光线和离轴光线在透镜中传播时对图像质量的影响规律。
我们知道对于凸透镜,由于存在球差,远轴光线将会有更长的光程,汇聚在与近轴光线不同的焦平面上。
不同散射角的光线偏离程度不同,这就使得到的图像模糊。
另一方面,如果我们只用近轴光线成像,所带有样品的信息量也很少,不利于对样品的研究。
因此,一幅质量好的图像中我们希望收集多的子波,又希望这些子波在传递过程中保持原有的特征,即振幅和相位没有大的改变,这样,大量的子波再次叠加合成后的图像就能最好地反映样品的特征。
成像的最终目的是在观察面上尽量复原样品的信息。
6.4 传递函数6.4.1 基本概念采用“传递”来描述成像过程的处理是为了数学上的方便,成像过程可以表达成“传递函数”求解,因而样品出射波函数经过传递函数处理后就得到像函数。
理想的成像过程中物体被成比例放大,没有畸变。
因此理想透镜的传递函数就是线性函数,简单写为T(K)=1。
不幸的是,现实中使用的透镜系统都是存在很多是图像失真的因素,例如像差,尤其是电磁透镜的球差难以消除,这样电镜成像中都有像差问题,只是在以往的成像过程这个问题不突出。
当我们要研究高分辨图像时,相差所带来的影响已经严重影响了我们对图像的采集和解读。
图像传递函数(contrast transfer function)就是包含了各种造成图像失真因素的函数,它是一个与物镜的球差、色差、电子束的发散度、电子束波长和成像位置(离焦量)有关的函数,它随着空间频率在+1与-1之间来回震荡。
实际成像系统图像将发生非比例变化,影响因素主要有:电镜的球差,用球差系数Cs表示(spherical aberration coefficient)成像时的焦距位置,用离焦量△f 表示 (defocus)偏离正焦的距离加速电压,它改变了电子束的波长λ电子束发散角α透镜的光栏尺寸D综合各影响因素的传递函数表达式为:上式有可以差分成每个部分函数的表达式,分别是研究T(K)的函数图像及特点将有助于理解成像过程的影响因素。