用三线摆法测定物体的转动惯量

实验4-3 用三线扭摆法测定物体的转动惯量转动惯量是刚体转动惯性大小的量度，它与刚体的质量、转轴位置及质量相对转轴的分布情况有关。

对于形状简单规则的刚体，测出其尺寸和质量，可用数学方法计算出转动惯量，而对形状复杂的刚体用数学方法求转动惯量非常困难，一般要通过实验方法来测定。

三线扭摆法测转动惯量是一种简单易行的方法。

【实验目的】1．学会使用三线扭摆法测定圆盘和圆环绕其对称轴的转动惯量。

2．学习使用MUJ-5B 计时计数测速仪测量周期。

3．研究转动惯量的叠加原理及应用。

【实验器材】三线扭摆、钢直尺、游标卡尺、水准仪、钢圆环、铝圆环、MUJ-5B 计时计数测速仪。

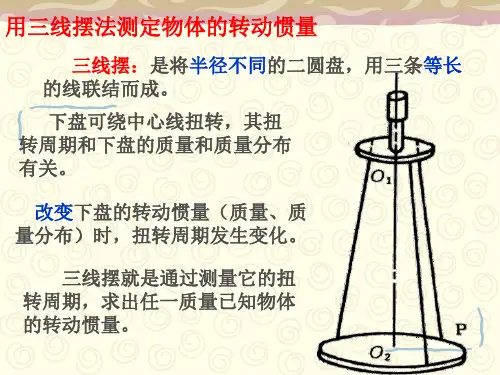
【实验原理】三线扭摆装置如图4-3-1a 所示。

上、下两个圆盘均处于水平，圆盘A 的中心悬挂在支架的横梁上，圆盘B 由三根等长的弦线悬挂在A 盘上。

三条弦线的上端和下端分别在A 圆盘和B 圆盘上各自构成等边三角形，且两个等边三角形的中心与两个圆盘的圆心重合。

A 盘可绕自身对称轴12O O 转动，若将A 盘转动一个不大的角度，通过弦线作用将使B 盘摆动，B 盘一方面绕轴12O O 转动，同时又在铅直方向上做升降平动，其摆动周期与B 盘的转动惯量大小有关。

设B 盘的质量是0m ，当它从平衡位置开始向某一方向转动角度θ时，上升高度为h （如图4-3-1b 所示），那么B 盘增加的势能为=p E 0m gh (4-3-1)这时B 圆盘的角速度为d dtθ，B 盘的动能为 201()2K d E J dtθ= (4-3-2) 式中0J 是B 盘绕自身中心轴的转动惯量。

如果略去摩擦力，则圆盘系统的机械能守恒，即2001()2d J m gh dtθ+= 常量 (4-3-3) 设悬线长为l ，上圆盘悬线到盘心的距离为r ，下圆盘悬线到盘心的距离为R 。

当下圆盘B 转一小角度θ（05<）时，圆盘上升高度h ，从上盘a 点向下作垂线，与升高前、后的下盘分别交于c 、1c ，悬线端点b 移到位置1b ，因而下盘B 上升高度为1h ac ac =-1212)()(ac ac ac ac +-= (4-3-4)因为 22222()()()()ac ab bc l R r =-=--2221111()()()ac ab b c =-222(2cos )l R r Rr θ=-+- 所以21122sin ()2(1cos )2Rr Rr h ac ac ac ac θθ⨯-==++ (4-3-5)在悬线l 较长而B 盘的扭转角θ很小时，有12ac ac H +≈， sin()22θθ≈其中H 为两圆盘之间的距离。

《用三线摆法测定物体的转动惯量》的示范报告
一、实验目的
本次实验的目的是使用三线摆法来测量物体的转动惯量。

二、实验原理
三线摆定律是一种使用频率敏感网络来测定物体转动惯量的力学原理。

它规定，一个物体如果经过特定角度的摆动旋转，其转动惯量和角速度的乘积是恒定的，这是物体的允许转动能量的最大值。

由此可以用来测量物体的转动惯量。

三、实验步骤
1.准备实验设备：普通支架、振子、底座、重量探头、小型马达等实验设备。

2.根据实验要求，按照规定的尺寸安装摆放实验设备，即将普通支架、振子、底座、重量探头和小型马达依次摆放设备，在摆放时要求牢固，使实验设备不会因振动而变形或改变大小。

3.根据三线摆定律，把小型马达的电源开关打开，比如设置110V的电源，使小型马达向相应方向运转起来。

4.不断调整实验设备的恒定摆放角度，观察马达的转速，然后写下每次实验参数。

5.根据实验参数，以及三线摆定律，用计算机计算物体的转动惯量，将结果写入文件中。

四、实验结果
根据实验参数，本次实验的转动惯量的结果如图：
五、总结
通过本次实验，可以熟悉三线摆测定物体转动惯量的实验原理与测量方法，了解物体转动动量的大小变化和转动频率之间的关系，并能够掌握利用物理原理测量物体动量的能力。

《用三线摆法测定物体的转动惯量》简明实验报告实验目的：通过使用三线摆法，测定不同物体的转动惯量，并探究物体质量、几何形状及质心位置对转动惯量的影响。

实验原理：转动惯量是描述物体转动惯性的物理量，表示了物体对转动所表现出的惯性大小。

对于一个质量为m、质心到转轴距离为r的物体，其转动惯量可以通过以下公式计算得出：I=m*r^2而对于一个不规则形状的物体，可以通过将其分解为一组质点，然后分别计算每个质点的转动惯量，并将其求和来得到总转动惯量：I=∑(m_i*r_i^2)在使用三线摆法进行测量时，需要固定物体在转轴上，并通过三根细线将物体悬挂起来。

当物体开始转动时，通过测量物体的摆动周期T和细线长度L，可以利用以下公式计算出转动惯量：I=(T^2*m*g*L)/(4π^2)实验装置：1.一个三线摆装置2.不同形状、不同质量的物体（如圆环、长方体、球体等）3.量角器4.绳子5.计时器6.秤实验步骤：1.将三线摆装置固定在桌面上，并调整好其水平度。

2.选择一个物体，将其通过一根细线绑在摆装置上，并调整好细线的长度，使得物体可以自由摆动。

3.将量角器放在与物体摆动平面垂直的位置，用来测量摆动的振幅角。

4.将绳子固定在物体上，并通过一张纸卡片保持绳子长度不变。

这样可以控制绳子长度的一致性。

5.用计时器测量物体的摆动周期T，反复测量多次以取得平均值。

6.用秤测量物体的质量m，并记录下来。

7.将摆装置往一侧推动，观察物体的摆动情况。

如果摆动不稳定，要重新调整摆装置和细线的位置。

8.重复步骤2-7，测量其他不同形状、不同质量的物体。

实验结果：根据测量得到的摆动周期T、细线长度L、质量m以及重力加速度g，可以计算出物体的转动惯量I。

将测量结果整理成表格，并绘制转动惯量与物体质量、几何形状及质心位置的关系图。

实验讨论：通过实验结果可以看出，质量、几何形状及质心位置都对物体的转动惯量有影响。

质量越大的物体，其转动惯量也越大；几何形状越复杂的物体，其转动惯量也越大；质心离转轴越远的物体，其转动惯量也越大。

三线摆法测试物体的转动惯量【一】实验目的1. 学会用三线摆测定物体的转动惯量。

2. 学会用累积放大法测量周期运动的周期。

3. 验证转动惯量的平行轴定理。

【二】实验仪器及使用方法三线摆、水准仪、停表、米尺、游标卡尺、物理天平以及待测物体等。

1． DH 4601转动惯量测试仪 1台 2． 实验机架 1套 3． 圆环 1块 4． 圆柱体 2个仪器操作打开电源, 程序预置周期为T=30（数显）, 即: 小球来回经过光电门的次数为T=2n+1次。

据具体要求, 若要设置50次, 先按“置数”开锁, 再按上调（或下调）改变周期T, 再按“置数”锁定, 此时, 即可按执行键开始计时, 信号灯不停闪烁, 即为计时状态, 当物体经过光电门的周期次数达到设定值, 数显将显示具体时间, 单位“秒”。

须再执行“50”周期时, 无须重设置, 只要按“返回”即可回到上次刚执行的周期数“50”, 再按“执行”键, 便可以第二次计时。

（当断电再开机时, 程序从头预置30次周期, 须重复上述步骤）【三】实验原理图1是三线摆实验装置的示意图。

上、下圆盘均处于水平, 悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定, 下圆盘可绕中心轴作扭摆运动。

当下盘转动角度很小, 且略去空气阻力时, 扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴的转动惯量(推导过程见本实验附录)。

2002004T H gRr m I π=（4-1） 式中各物理量的意义如下: 为下盘的质量；、分别为上下悬点离各自圆盘中心的距离；为平衡时上下盘间的垂直距离；为下盘作简谐运动的周期, 为重力加速度（在杭州地区）。

将质量为的待测物体放在下盘上, 并使待测刚体的转轴与轴重合。

测出此时摆运动周期和上下圆盘间的垂直距离。

同理可求得待测刚体和下圆盘对中心转轴轴的总转动惯量为： 212014)(T HgRr m m I π+=（4-2） 如不计因重量变化而引起悬线伸长, 则有。

大学物理实验-用三线摆法测定物体的转动惯量用三线摆法测定物体的转动惯量转动惯量是刚体在转动中惯性大小的量度，它与刚体的总质量、形状大小、密度分布和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，用数学方法计算它的转动惯量非常困难，大都用实验方法测定。

例如：机械零部件、电机转子及枪炮弹丸等。

因此学会刚体转动惯量的测定方法，具有重要的实际意义。

测量转动惯量，一般是使刚体以一定形式运动，通过表征这种运动特征的物理量与转动惯量的关系，进行转换测量。

常用的测量方法有三线扭摆法、单线扭摆法、塔轮法等。

本实验采用三线扭摆法，由摆动周期及其他参数的测定计算出物体的转动惯量。

为了便于和理论值进行比较，实验中的被测物体一般采用形状规则的物体。

【实验目的】1、掌握三线扭摆法测量物体转动惯量的原理和方法；2、研究物体的转动惯量与其质量、形状（密度均匀时）及转轴位置的关系；3、学会正确测量长度、质量和时间的方法。

【实验仪器】FB210型三线摆转动惯量测定仪、游标卡尺、钢卷尺、数字毫秒计、物理天平、待测物体等。

【实验原理】图1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O '作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴O O '的转动惯量(推导过程见本实验附录)。

202004T H gRr m I π= （1） 式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各自圆盘中心的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重力加速度（在杭州地区g =9.793m/s 2）。

图1三线摆实验装置图将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

用三线摆法测定物体的转动惯量剖析引言转动惯量是物体围绕某个轴的旋转惯性，是物体自身的性质。

在物体的旋转运动中，转动惯量起着至关重要的作用。

因此，精确测定物体的转动惯量是非常必要的。

一种常用的测定转动惯量的方法是采用三线摆法。

本文将对三线摆法的实验原理、实验步骤和实验结果进行详细剖析。

实验原理为了精确测定物体的转动惯量，我们需要知道一些基本原理。

下面是需要了解的实验原理：1. 三线摆法的原理三线摆法是利用物体转动的运动学原理来测定物体转动惯量的方法。

在三线摆法中，物体被挂在三个不同的固定点上，使得物体能够以不同的转动轴进行旋转。

通过测定物体绕三个不同的轴旋转所需的时间，可以确定物体的转动惯量。

2. 物体转动惯量的计算公式一般来说，物体转动惯量可以通过物体的质量、尺寸和形状来计算。

以下是物体转动惯量的计算公式：对于直线对称的物体，如圆环和圆盘，其转动惯量可以使用以下公式计算：I=mR²其中，I是转动惯量，m是物体的质量，R是物体的半径。

此外，对于形状不规则的物体，可以使用三维积分公式来计算转动惯量。

3. 质心的作用质心是物体的平衡点，是物体重心位置的体现。

在旋转运动中，物体转动轴应该在质心处。

这是因为物体围绕质心旋转时具有最小的转动惯量。

实验步骤1. 实验器材的准备在开始实验之前，请准备以下器材：（1）三条细线，长度应该相等，可以通过测量来确认。

（2）一块直线对称的圆盘（也可以使用其他形状的物体）。

（3）一台计时器。

（4）一把直尺。

2. 实验过程（1）用一条细线将圆盘挂在一个固定点上。

固定点可以是桌角、悬挂在屋顶上的吊钩或者其他固定点。

（2）利用另外两条细线将圆盘挂在其他两个点上，注意每个点应该在不同的位置，以便进行不同的旋转。

（3）调整圆盘的位置，使得每条细线都恰好与圆盘表面接触，然后仔细调整圆盘的位置使得它与水平面垂直。

（4）将圆盘在三个不同的点上挂起来，预备进行实验。

（5）选定一个固定点为旋转轴，将圆盘拉到一边，然后松开，记录下圆盘绕选定轴旋转一周所需的时间t1。

三线摆测物体转动惯量【实验原理】转动惯量是刚体在转动过程中惯性大小的量度。

1.对于质量分布均匀，几何形状简单的刚体，可直接用公式计算其转动惯量。

即dV r J ⎰=ρ2 （1）2.对于质量分布不均匀和形状复杂的刚体，实际科研和生产中则采用实验方法测定。

本实验利用三线摆测量任意形状的物体相对于某一个转轴的转动惯量。

图1为三线摆，将待测物体置于底盘上，将顶盘绕垂直于其表面并通过其竖直中心轴线转过一个角度是，由于受重力和线的张力作用，将牵动底盘作往复扭转，同时底盘的质心沿转轴升降。

扭转的周期和与底盘（和盘上物体）的转动惯量有关，其测量公式为01J J J -= （2）其中， 整体转动惯量 ()21214T HgRr m m J π'+=， （3）底盘对竖直中心轴的转动惯量21204T HmgRr J π= （4）上述公式中，m 为底盘质量，h 为转动时上升的高度，H 为顶盘与底盘之间的垂直距离，r 为顶盘的悬点到盘中心的距离，R 为底盘悬点到盘中心的距离。

0T 为地盘的转动周期，1T 为待测物体和底盘共同的转动周期。

【实验仪器】三线摆、秒表、钢卷尺、游标卡尺、水平仪、待测圆环。

【实验步骤】1. 用游标卡尺测量顶盘悬孔之间距离b 和底盘孔之间距离d ,用米尺测量底盘几何直径，各三次。

2. 用游标卡尺测量圆环的内、外直径各一次。

3. 分别查出底盘和圆环的质量m 和m ′4. 用水平仪调节底盘水平，然后用钢卷尺测量两盘之间的垂直距离。

5. 在静止的状态下，轻微转动顶盘约5º随即倒退回原处，底盘做小角度扭转，稳定后，在底盘经过平衡位置时按下秒表记作0周期，当底盘再一次以同方向经过平衡位置时为完成第一次全振动。

测出完成50次全振动所需要的时间，共测三次，填入数据表。

求出底盘转动周期0T 。

6. 将待测圆环置于底盘上，使其质心通过圆盘中心，重复步骤4、5，测出周期1T 。

【数据记录及处理】1.数据记录2.计算计算底盘加环的转动惯量J 1 计算换的转动惯量J换的转动惯量理论值()()22228121外内外内理D D m R R m J +'=+'=测量值与理论之比较，百分差E。

实验4 用三线摆测定物体的转动惯量[摘要]转动惯量是表征刚体转动特性的物理量，是刚体转动惯性大小的量度，它与刚体质量的大小、转轴的位置和质量对于转轴的分布等有关。

对于形状简单的刚体，可以通过数学方法计算出它绕特定转轴的转动惯量。

但对于形状复杂的刚体，用数学方法计算它的转动惯量就非常困难，有时甚至不可能，所以常用实验方法测定。

因此，学会测定刚体转动惯量的方法，具有实用意义。

测定刚体转动惯量的方法有多种，本实验采用三线扭摆法。

[实验目的、要求]学会用三线扭摆法测定物体的转动惯量。

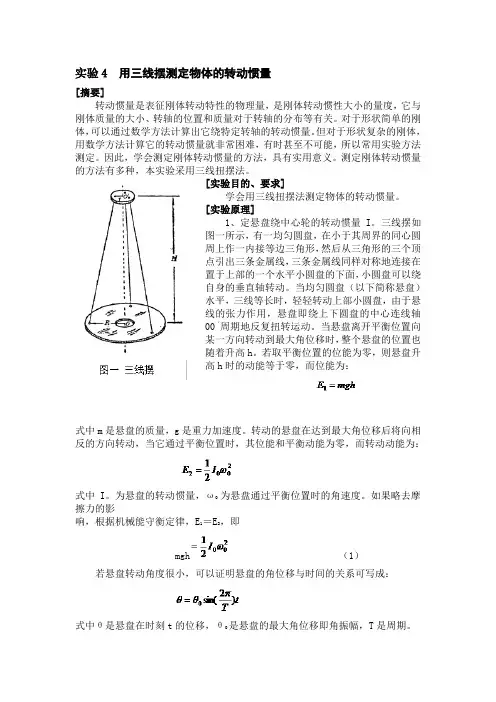
[实验原理]1、定悬盘绕中心轮的转动惯量I。

三线摆如图一所示，有一均匀圆盘，在小于其周界的同心圆周上作一内接等边三角形，然后从三角形的三个顶点引出三条金属线，三条金属线同样对称地连接在置于上部的一个水平小圆盘的下面，小圆盘可以绕自身的垂直轴转动。

当均匀圆盘（以下简称悬盘）水平，三线等长时，轻轻转动上部小圆盘，由于悬线的张力作用，悬盘即绕上下圆盘的中心连线轴00‘周期地反复扭转运动。

当悬盘离开平衡位置向某一方向转动到最大角位移时，整个悬盘的位置也随着升高h。

若取平衡位置的位能为零，则悬盘升高h时的动能等于零，而位能为：式中m是悬盘的质量，g是重力加速度。

转动的悬盘在达到最大角位移后将向相反的方向转动，当它通过平衡位置时，其位能和平衡动能为零，而转动动能为：式中I。

为悬盘的转动惯量，ω为悬盘通过平衡位置时的角速度。

如果略去摩擦力的影响，根据机械能守衡定律，E1＝E2，即mgh（1）若悬盘转动角度很小，可以证明悬盘的角位移与时间的关系可写成：式中θ是悬盘在时刻t的位移，θ是悬盘的最大角位移即角振幅，T是周期。

角速度ω是角位移θ对时间的一阶导数，即：在通过平衡位置的瞬时，角速度的绝对值是：（2）根据（1）和（2）式得：（3）设l是悬线之长，R是悬盘点到中心的距离，由图二可得：因为：得：在偏转角很小时而所以（4）将（4）式代人（3）式得：（5）这是测定悬盘绕中心轴转动的转动惯量计算公式。