大学物理实验《用三线摆测量刚体的转动惯量》

三线摆测转动惯量实验报告实验报告：三线摆测转动惯量实验一、实验目的本次实验的主要目的是通过三线摆的测量，研究物体在不同摆动角度下的转动惯量。

转动惯量是描述物体旋转特性的一个重要参数，对于理解物体的运动规律和动力学性能具有重要意义。

二、实验原理1. 三线摆的构造三线摆是由三条相互垂直的细线组成，其中两条细线固定在同一端点，另一条细线则通过一个支点悬挂。

当三线摆摆动时，细线的张力会产生扭矩，使得摆锤绕支点旋转。

2. 转动惯量的计算公式转动惯量的计算公式为：I = m * r^2,其中m为物体的质量，r为物体的半径。

在本实验中，我们将通过测量三线摆在不同摆动角度下的周期和角速度，从而求得物体的转动惯量。

三、实验步骤与结果分析1. 实验准备(1) 准备三线摆、计时器、直尺等实验工具。

(2) 将三线摆调整至水平状态，使两条细线的夹角为90°。

(3) 在三线摆的一端挂上质量为m的小球。

(4) 将三线摆调整至合适的初始位置，使其摆动幅度较小。

2. 实验过程与数据记录(1) 以一定的时间间隔记录三线摆的周期T;(2) 以一定的时间间隔记录三线摆的角速度ω。

(3) 根据公式I = 2π/T * ω^2 * r,计算出小球的转动惯量I;(4) 重复以上步骤，分别测量三线摆在不同摆动角度下的数据。

3. 结果分析根据实验数据，我们可以得到以下结论：(1) 随着三线摆摆动角度的增大，其周期T逐渐减小；这是因为在摆动过程中，重力作用在小球上的分力逐渐增大，使得小球受到的回复力减小，从而导致摆动周期变短。

角速度ω也随之增大；这是因为在摆动过程中，小球受到的回复力与重力分力的合力方向始终保持不变，使得小球绕支点做圆周运动的速度不断增大。

因此，我们可以得出结论：物体在不同摆动角度下的转动惯量与其固有属性有关。

曲阜师范大学实验报告实验日期：2020.5.24姓名：方小柒 年级：19级实验时间：8: 30-12： 00**********专业：化学类实验题目：三线摆测刚体转动惯量一、 实验目的：1. 学会用三线摆法测定物体转动惯量原理和方法。

2. 学会时间、长度、质量等基本物理蛩的测蛩方法以及仪器的水平调节。

二、 实验仪器：三线摆，待测物体（圆环和两个质量和形状相同圆柱），游标卡尺，米尺，电子秒表，水平仪三、 实验原理：转动惯堂是物体转动惯性的量度，物体对某轴的转动惯量越大，则绕该轴 转动时，角速度就越难改变。

三线摆装罝如阁所示，上下两盘调成水平后，两盘圆心在同一垂直线0102 上。

下盘可绕中心轴线0102扭转，其扭转周期T 和下盘的质量分布有关，当改 变下盘的质量分布时，其绕中心轴线0102的扭转周期将发生变化。

三线摆就是通过测萤它的扭转周期去求任意质量已知物体的转动惯量的。

-T L-<三摆-线示，意閱当下盘转动角度 0很小，且略去空气阻力时，悬线伸长不计，扭摆的运动可近似看作简谐运动。

根据能萤守恒记律和刚体转动⅛律均可以得出物体绕中心 轴00'的转动惯量：m o ∂Rr T 2下盘：J 0=(m0 + m')gRrrrt2T I下盘+圆环：J1= 4π&— ■■■— [(m0+ m)Γl2 — mΓ2]圆环：J= J i-Jo=4πH(条件：θ≤5°,空气阻力不计，悬线伸长不计，圆环与下盘中心重合)因此，通过长度、质量和时间的测量，便可求出刚体绕某轴的转动惯萤。

四、实验内容：1.了解三线摆原理以及有关三线摆实验器材的知识。

2. 用三线摆测萤圆环的转动惯萤，并验证平行轴记理(1) 测定仪器常数H、R、r恰当选择测虽仪器和用具，减小测量不确定度。

A拟实验步骤，确保三线摆上、下圆盘的水平，是仪器达到最佳测萤状态。

(2) 测萤下圆盘的转动惯蚩线摆上方的小圆盘，使其绕自身转动一个角度，借助线的张力使下圆盘作扭摆运动，而避免产生左右晃动。

实验２ 用三线摆测量刚体的转动惯量转动惯量是刚体转动时惯性大小的量度，它与刚体的质量分布和转轴的位置有关。

对于质量分布均匀、外形不复杂的刚体，测出其外形尺寸及质量，就可以计算出其转动惯量；而对于外形复杂、质量分布不均匀的刚体，其转动惯量就难以计算，通常利用转动实验来测定。

三线摆就是测量刚体转动惯量的基本方法之一。

一. 实验目的1. 学会正确测量长度、质量和时间。

2. 学习用三线摆测量圆盘和圆环绕对称轴的转动惯量。

二. 实验仪器三线摆仪、米尺、游标卡尺、数字毫秒计、气泡水平仪、物理天平和待测圆环等。

三. 实验原理图3-2-1是三线摆实验装置示意图。

三线摆是由上、下两个匀质圆盘，用三条等长的摆线（摆线为不易拉伸的细线）连接而成。

上、下圆盘的系线点构成等边三角形，下盘处于悬挂状态，并可绕OO ‘轴线作扭转摆动，称为摆盘。

由于三线摆的摆动周期与摆盘的转动惯量有一定关系，所以把待测样品放在摆盘上后，三线摆系统的摆动周期就要相应的随之改变。

这样，根据摆动周期、摆动质量以及有关的参量，就能求出摆盘系统的转动惯量。

设下圆盘质量为0m ，当它绕OO ＇扭转的最大角位移为o θ时，圆盘的中心位置升高h ，这时圆盘的动能全部转变为重力势能，有：gh m E P 0= （g 为重力加速度）当下盘重新回到平衡位置时，重心降到最低点，这时最大角速度为0ω，重力势能被全部转变为动能，有：20021ωI E K =式中0I 是下圆盘对于通过其重心且垂直于盘面的OO ‘轴的转动惯量。

如果忽略摩擦力，根据机械能守恒定律可得：200021ωI gh m =（3-2-1）设悬线长度为l ，下圆盘悬线距圆心为R 0，当下圆盘转过一角度0θ时，从上圆盘B 点作下圆盘垂线，与升高h 前、后下圆盘分别交于C 和C 1，如图3-2-2所示，则：12!21)()(BC BC BC BC BC BC h +-=-=∵ 22222)()()()(r R AC AB BC --=-=102102sin 4)cos 1(2BC BC Rr BC BC Rr h +=+-=θθ 在扭转角0θ很小，摆长l 很长时，sin 22θθ≈，而BC+BC 1≈2H ，其中)cos 2()()()(022********θRr r R C A B A BC -+-=-=H=22)(r R l -- （H 为上下两盘之间的垂直距离）则H Rr h 220θ=（3-2-2） 由于下盘的扭转角度0θ很小（一般在5度以内），摆动可看作是简谐振动。

用三线摆测刚体转动惯量实验报告实验报告：用三线摆测刚体转动惯量实验目的：1. 掌握用三线摆测量刚体转动惯量的方法。

2. 验证刚体转动惯量与质量、形状和转动轴位置的关系。

实验器材：1. 刚体（如圆盘或长方体）；2. 三根细线；3. 三个线圈（用于固定细线）；4. 计时器；5. 重锤；6. 质量砝码；7. 万能电表。

实验原理：根据刚体转动惯量的定义，刚体绕固定轴的转动惯量可以通过实验方法进行测量。

而三线摆正是一种常用的测量刚体转动惯量的实验方法。

实验步骤：1. 找一个悬挂点，将三根细线的一端绑在悬挂点上，使它们呈120度夹角，且每两根线间的夹角均为120度。

确保三根线的长度相等。

2. 将刚体沿着转动轴固定在三线悬挂点的下方，使其能够自由转动，且刚体转动轴垂直于实验台面。

3. 用三个线圈将每根细线的另一端固定在刚体上，确保它们与刚体形成120度的夹角。

4. 将重锤挂在其中任意一根细线上，并使其恰好与水平方向垂直。

重锤的作用是增大刚体转动的振幅，使测量更加准确。

5. 将刚体用手指轻轻推动，使其围绕转动轴做小幅度摆动，并利用计时器测量刚体做10个摆动的时间t。

6. 重复步骤5，记录不同的时间t（可为5次或更多次），并求出它们的平均值T。

7. 在实验过程中，可改变刚体的转动轴位置、刚体的质量以及刚体的形状，记录对应的时间t和平均值T。

实验数据处理：1. 计算每次摆动的周期T，即T = t / 10。

2. 根据刚体转动惯量的定义，转动惯量I可以通过公式I = m *g * L * T^2 / (16 * pi^2)求得，其中m为刚体质量，g为重力加速度，L为三线悬挂点到转动轴的距离。

3. 利用万能电表测量刚体质量并记录。

4. 在实验过程中，改变刚体的转动轴位置、质量和形状，记录相应的数据，然后绘制转动惯量I与不同因素的关系图。

实验注意事项：1. 实施实验前应检查细线和线圈是否牢固。

2. 在实验过程中，需要保持摆动的幅度相对较小，以减小摆动角度对结果的影响。

大学物理实验-用三线摆法测定物体的转动惯量用三线摆法测定物体的转动惯量转动惯量是刚体在转动中惯性大小的量度，它与刚体的总质量、形状大小、密度分布和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，用数学方法计算它的转动惯量非常困难，大都用实验方法测定。

例如：机械零部件、电机转子及枪炮弹丸等。

因此学会刚体转动惯量的测定方法，具有重要的实际意义。

测量转动惯量，一般是使刚体以一定形式运动，通过表征这种运动特征的物理量与转动惯量的关系，进行转换测量。

常用的测量方法有三线扭摆法、单线扭摆法、塔轮法等。

本实验采用三线扭摆法，由摆动周期及其他参数的测定计算出物体的转动惯量。

为了便于和理论值进行比较，实验中的被测物体一般采用形状规则的物体。

【实验目的】1、掌握三线扭摆法测量物体转动惯量的原理和方法；2、研究物体的转动惯量与其质量、形状（密度均匀时）及转轴位置的关系；3、学会正确测量长度、质量和时间的方法。

【实验仪器】FB210型三线摆转动惯量测定仪、游标卡尺、钢卷尺、数字毫秒计、物理天平、待测物体等。

【实验原理】图1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O '作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴O O '的转动惯量(推导过程见本实验附录)。

202004T H gRr m I π= （1） 式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各自圆盘中心的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重力加速度（在杭州地区g =9.793m/s 2）。

图1三线摆实验装置图将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

(报告)用三线摆法测量刚体的转动惯量(2)
实验步骤：
1. 在水平桌面上放置一个圆柱形的刚体，用三线摆法进行转动惯量的测量。

2. 在刚体上固定两个不同距离的细绳，使得两个细绳成一个角度固定在圆柱的一个半径上，并且这个半径垂直于水平面。

3. 将第三个细绳放置到圆柱中心，将其拉紧，使得圆柱沿着第三个细绳进行转动。

4. 测量第三个细绳与水平面的夹角，记为θ。

5. 将圆柱缓慢转动，并测量其转动的周期T和振幅A。

6. 计算圆柱转动的角加速度α=A/(T/4)^2，并根据三线摆法的
公式I=ML^2/(αsinθ)计算刚体的转动惯量I。

实验注意事项：
1. 在测量前需要确保刚体的重心位于三根细绳的交点处，避免出现偏差。

2. 测量时需要保持细绳的水平，避免影响实验结果。

3. 转动时需要保持圆柱的稳定，避免出现晃动或者滑动等情况。

4. 在测量过程中需要注意安全，避免刚体掉落或者细绳损坏等情况。

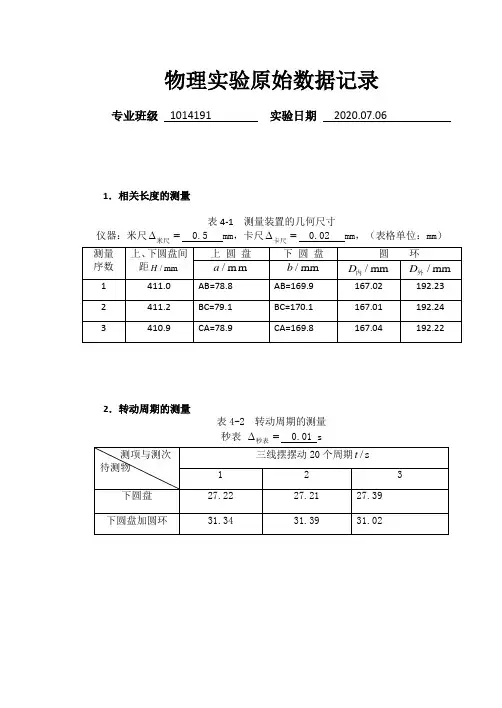
物理实验原始数据记录专业班级1014191 实验日期2020.07.061．相关长度的测量表4-1 测量装置的几何尺寸仪器：米尺∆=米尺 0.5 mm，卡尺∆=卡尺0.02 mm，（表格单位：mm）2．转动周期的测量表4-2 转动周期的测量秒表∆=秒表0.01 s实验名称三线摆法测刚体转动惯量实验名称： 三线摆法测刚体转动惯量 实验时间：2020..7.6 小组成员：张振勇实验地点：实验目的：1. 掌握用三线摆测定物体转动惯量的方法 仪器、设备和材料：三线摆，米尺，游标卡尺，秒表，游标卡尺等【实验原理】三线摆的结构如图4-1所示，用三条等长的线，把两个半径不同的圆盘对称地悬挂在横梁上，横梁由立柱和底座支承着。

上圆盘可固定，匀质的下圆盘可绕两圆盘的中心轴线 'OO 作扭转，此过程也就是圆盘的势能、动能的转化过程。

扭转的周期由下圆盘（包括置于其上的物体）的转动惯量决定。

三线摆就是通过测量它的扭转周期和有关的几何参数，而求出任一己知物体的转动惯量。

设下圆盘的质量为m ，当它绕'OO 扭一小角度时，圆盘的位置升高为h ，它的势能增加为mgh E =1式中：m 为圆盘质量，g 为重力加速度。

当圆盘回到平衡位置时，01=E ，只有转动动能220012E J ω=0J 为下圆盘对于通过其重心且垂直于盘面轴的转动惯量,0ω是圆盘通过平衡位置时的角速度。

如果不考虑摩擦阻力，根据机械能守恒定律得：20012mgh J ω=（４-１） 若扭转的角度足够小，我们可以把下圆盘的运动看作简谐运动，则圆盘的角位移与时间的关系为⎪⎭⎫⎝⎛=t Tπθθ2sin 0 式中：θ是圆盘在时间t 的角位移，0θ是最大角位移，T 是一完全振动的周期。

圆盘的最大角速度为图４-1 三线摆002θπωT=(４-2) 各几何参数之间的关系如图４-2所示。

设悬线长为l ，上、下圆盘的垂直距离为H ，上、下两圆盘上的悬点离各自圆盘中心的距离为r 、R 。

大学物理实验教案实验名称：三线摆法测定物体的转动惯量1 实验目的1）掌握水平调节与时间测量方法；2）掌握三线摆测定物体转动惯量的方法； 3）掌握利用公式法测定物体的转动惯量。

2 实验仪器三线摆装置 计数器 卡尺 米尺 水平器 3 实验原理3.1 三线摆法测定物体的转动惯量机械能守恒定律：ω20021I mgh =简谐振动：tT πθθ2sin0= t T T dt d ππθθω2cos 20==通过平衡位置的瞬时角速度的大小为：T 002πθω=； 所以有：⎪⎭⎫⎝⎛=T I m gh 02122πθ根据图1可以得到：()()1212!BC BC BC BC BC BC h +-=-=()()()()22222r R l AC AB BC --=-=从图2可以看到：根据余弦定律可得()()022211cos 2θRr r R C A -+= 所以有：()()()()02222112121cos 2θRr r R l C A B A BC -+-=-= 整理后可得：102102sin 4)cos 1(2BC BC Rr BC BC Rr h +=+-=θθH BC BC 21≈+；摆角很小时有：2)2sin(00θθ= 所以：H Rr h 220θ=整理得：2204T H mgRr I π=；又因3b R =，3a r = 所以：22012T H mgab I π=若其上放置圆环，并且使其转轴与悬盘中心重合，重新测出摆动周期为T 1和H 1则：2112112)(T H gab M m I π+=待测物的转动惯量为： I= I 1-I 03.2 公式法测定物体的转动惯量圆环的转动惯量为：()D D M I 222181+=4 教学内容4.1 三线摆法测定圆环绕中心轴的转动惯量1)用卡尺分别测定三线摆上下盘悬挂点间的距离a 、b （三个边各测一次再平均）； 2)调节三线摆底坐前两脚螺丝使上盘水平3)调节三线摆悬线使悬盘到上盘之间的距离H 大约50cm 左右，并调节悬盘水平； 4)用米尺测定悬盘到上盘三线接点的距离H ；5)让悬盘静止后轻拨上盘使悬盘作小角度摆动（注意观察其摆幅是否小于10度，摆动是否稳定不摇晃。

⼤学物理实验-⽤三线摆法测定物体的转动惯量⽤三线摆法测定物体的转动惯量转动惯量是刚体在转动中惯性⼤⼩的量度，它与刚体的总质量、形状⼤⼩、密度分布和转轴的位置有关。

对于形状较简单的刚体，可以通过数学⽅法算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，⽤数学⽅法计算它的转动惯量⾮常困难，⼤都⽤实验⽅法测定。

例如：机械零部件、电机转⼦及枪炮弹丸等。

因此学会刚体转动惯量的测定⽅法，具有重要的实际意义。

测量转动惯量，⼀般是使刚体以⼀定形式运动，通过表征这种运动特征的物理量与转动惯量的关系，进⾏转换测量。

常⽤的测量⽅法有三线扭摆法、单线扭摆法、塔轮法等。

本实验采⽤三线扭摆法，由摆动周期及其他参数的测定计算出物体的转动惯量。

为了便于和理论值进⾏⽐较，实验中的被测物体⼀般采⽤形状规则的物体。

【实验⽬的】1、掌握三线扭摆法测量物体转动惯量的原理和⽅法；2、研究物体的转动惯量与其质量、形状（密度均匀时）及转轴位置的关系；3、学会正确测量长度、质量和时间的⽅法。

【实验仪器】FB210型三线摆转动惯量测定仪、游标卡尺、钢卷尺、数字毫秒计、物理天平、待测物体等。

【实验原理】图1是三线摆实验装置的⽰意图。

上、下圆盘均处于⽔平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中⼼轴O O '作扭摆运动。

当下盘转动⾓度很⼩，且略去空⽓阻⼒时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中⼼轴O O '的转动惯量(推导过程见本实验附录)。

2002004T H gRrm I π= （1）式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各⾃圆盘中⼼的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重⼒加速度（在杭州地区g =9.793m/s 2）。

将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

三线摆法测定刚体的转动惯量一、实验简介转动惯量是刚体转动时惯性的量度，其量值取决于物体的形状、质量、质量分布及转轴的位置。

刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。

对于几何形状简单、质量分布均匀的刚体可以直接用公式计算出它相对于某一确定转轴的转动惯量。

对于任意刚体的转动惯量，通常是用实验方法测定出来的。

测定刚体转动惯量的方法很多，通常的有三线摆、扭摆、复摆等。

本实验要求学生掌握用三线摆测定物体转动惯量的方法,并验证转动惯量的平行轴定理。

二、实验原理图1三线摆结构示意图 图2下圆盘的扭转振动1—底座；2—底座上的调平螺丝；3—支杆；4—悬架和支杆连接的固定螺丝；5—悬架； 6—上圆盘悬线的固紧螺丝；7—上圆盘；8—悬线；9—下圆盘；10—待测金属环； 当上、下圆盘水平时，将上圆盘绕竖直的中心轴线O O 1转动一个小角度,借助悬线的张力使悬挂的大圆盘绕中心轴O O 1作扭转摆动。

同时，下圆盘的质心1O 将沿着转动轴升降，如上图中右图所示。

H 是上、下圆盘中心的垂直距离；h 是下圆盘在振动时上升的高度；α是扭转角。

显然，扭转的过程也是圆盘势能与动能的转化过程。

扭转的周期与下圆盘（包括置于上面的刚体）的转动惯量有关。

当下圆盘的扭转角α很小时，下圆盘的振动可以看作理想的简谐振动。

其势 能p E 和动能k E 分别为：0p E m gh =（1） 220011()()22k d dh E I m dt dt α=+ （2）式中0m 是下圆盘的质量，g 为重力加速度，h 为下圆盘在振动时上升的高度，ωα=dt d 为圆频率，dtdh 为下圆盘质心的速度，为圆盘对0I O O 1轴的转动惯量。

若忽略摩擦力的影响，则在重力场中机械能守恒：恒量=+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛gh m dt dh m dt d 0202021I 21α （3）因下圆盘的转动能远大于上下运动的平动能，于是近似有恒量=+⎪⎭⎫ ⎝⎛gh m dt d 020I 21α （4）又通过计算可得： H Rr 2h 2α= （5）将（5）代入（4）并对t 求导，可得：ααH I gRr m dt 0022d -= （6）该式为简谐振动方程，可得方程的解为：H I gRr m 002=ω （7）因振动周期ωπ2T 0=，代入上式得：H I gRr m T 002024=π 故有： 200024m gRr I T H π= （8） 由此可见，只要准确测出三线摆的有关参数0m 、R 、r 、H 和0T ，就可以精确地求出下圆盘的转动惯量0I 。

用三线摆法测定物体的转动惯量转动惯量是刚体在转动中惯性大小的量度，它与刚体的总质量、形状大小、密度分布和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，用数学方法计算它的转动惯量非常困难，大都用实验方法测定。

例如：机械零部件、电机转子及枪炮弹丸等。

因此学会刚体转动惯量的测定方法，具有重要的实际意义。

测量转动惯量，一般是使刚体以一定形式运动，通过表征这种运动特征的物理量与转动惯量的关系，进行转换测量。

常用的测量方法有三线扭摆法、单线扭摆法、塔轮法等。

本实验采用三线扭摆法，由摆动周期及其他参数的测定计算出物体的转动惯量。

为了便于和理论值进行比较，实验中的被测物体一般采用形状规则的物体。

【实验目的】1、掌握三线扭摆法测量物体转动惯量的原理和方法；2、研究物体的转动惯量与其质量、形状（密度均匀时）及转轴位置的关系；3、学会正确测量长度、质量和时间的方法。

【实验仪器】FB210型三线摆转动惯量测定仪、游标卡尺、钢卷尺、数字毫秒计、物理天平、待测物体等。

【实验原理】图1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O '作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴O O '的转动惯量(推导过程见本实验附录)。

2002004T H gRrm I π= （1）式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各自圆盘中心的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重力加速度（在地区g =9.793m/s 2）。

将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

测出此时下盘运动周期1T 和上下圆盘间的垂直距离H 。

用三线摆法测定物体的转动惯量转动惯量是刚体在转动中惯性大小的量度，它与刚体的总质量、形状大小、密度分布和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，用数学方法计算它的转动惯量非常困难，大都用实验方法测定。

例如：机械零部件、电机转子及枪炮弹丸等。

因此学会刚体转动惯量的测定方法，具有重要的实际意义。

测量转动惯量，一般是使刚体以一定形式运动，通过表征这种运动特征的物理量与转动惯量的关系，进行转换测量。

常用的测量方法有三线扭摆法、单线扭摆法、塔轮法等。

本实验采用三线扭摆法，由摆动周期及其他参数的测定计算出物体的转动惯量。

为了便于和理论值进行比较，实验中的被测物体一般采用形状规则的物体。

【实验目的】1、掌握三线扭摆法测量物体转动惯量的原理和方法；2、研究物体的转动惯量与其质量、形状（密度均匀时）及转轴位置的关系；3、学会正确测量长度、质量和时间的方法。

【实验仪器】FB210型三线摆转动惯量测定仪、游标卡尺、钢卷尺、数字毫秒计、物理天平、待测物体等。

【实验原理】图1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O '作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴O O '的转动惯量(推导过程见本实验附录)。

2002004T H gRrm I π= （1）式中各物理量的意义如下：0m 为下盘的质量；r 、R 分别为上下悬点离各自圆盘中心的距离；0H 为平衡时上下盘间的垂直距离；T 0为下盘作简谐运动的周期，g 为重力加速度（在杭州地区g =9.793m/s 2）。

将质量为m 的待测物体放在下盘上，并使待测刚体的转轴与O O '轴重合。

测出此时下盘运动周期1T 和上下圆盘间的垂直距离H 。

用三线摆测刚体转动惯量实验报告实验目的：1. 掌握使用三线摆测定刚体转动惯量的方法；2. 理解刚体转动惯量的概念及其在物体转动中的作用。

实验器材：1. 三线摆实验装置：包括一个固定在架子上的支持轴、一个可绕轴转动的支架；2. 不同形状和质量的刚体：如圆柱体、长方体等；3. 黄铜环：用于挂载刚体；4. 轻质细线：用于连接黄铜环和支架；5. 增重片：用于调整刚体的质量。

实验原理：1. 刚体转动惯量的定义：刚体绕轴的转动惯量J定义为刚体转动时，由质量分布带来的转动惯量关于转轴的积分，即J=∫r^2dm，其中r为质点到转轴的距离，dm为质量微元。

2. 三线摆实验方法：利用物体绕支撑点转动时的平衡条件，通过在不同位置附加不同质量的增重片，使物体绕转轴发生周期性摆动。

通过测量周期和刚体实际质量，计算出刚体的转动惯量。

实验步骤：1. 将三线摆装置安装于平稳的实验台上，并将刚体挂载在黄铜环上，使其悬吊在三线摆装置上；2. 调整黄铜环的位置，使刚体能够自由摆动，并找到刚体摆动的平衡位置；3. 测量刚体的长度L，以及黄铜环与刚体重心的距离d；4. 测量刚体的质量m，并记录刚体的形状；5. 在黄铜环上附加适量的增重片，使刚体产生微小摆动；6. 启动计时器，并记录刚体进行n个周期的时间T；7. 根据实验数据，计算刚体的转动惯量J=4π²(L+d)⁴m/nT²。

实验数据记录与处理：在进行实验时，根据实际情况记录以下数据：1. 刚体的形状、质量和长度；2. 增重片的质量；3. 进行n个周期的时间T。

根据记录的数据，利用实验原理中的公式计算刚体的转动惯量，并进行数据处理与分析。

实验注意事项：1. 实验过程中要小心操作，避免刚体与装置碰撞或摩擦造成误差；2. 实验时要确保刚体摆动的幅度足够小，以保证计算中的近似条件成立；3. 注意记录实验数据时的精确度，尽量减小测量误差；4. 实验完成后要对仪器进行清理，保持实验室的整洁。

图1三线摆实验装置示意图图2 三线摆原理图实验七用三线摆测量刚体的转动惯量【实验目的】1. 学会正确测量长度、质量和时间。

2. 学习用三线摆测量圆盘和圆环绕对称轴的转动惯量。

【实验器材】三线摆仪、米尺、游标卡尺、数字毫秒计、气泡水平仪、物理天平和待测圆环等。

【实验原理】转动惯量是刚体转动时惯性大小的量度，它与刚体的质量分布和转轴的位置有关。

对于质量分布均匀、外形不复杂的刚体，测出其外形尺寸及质量，就可以计算出其转动惯量；而对于外形复杂、质量分布不均匀的刚体，其转动惯量就难以计算，通常利用转动实验来测定。

三线摆就是测量刚体转动惯量的基本方法之一。

图1是三线摆实验装置示意图。

三线摆是由上、下两个匀质圆盘，用三条等长的摆线（摆线为不易拉伸的细线）连接而成。

上、下圆盘的系线点构成等边三角形，下盘处于悬挂状态，并可绕OO‘轴线作扭转摆动，称为摆盘。

由于三线摆的摆动周期与摆盘的转动惯量有一定关系，所以把待测样品放在摆盘上后，三线摆系统的摆动周期就要相应的随之改变。

这样，根据摆动周期、摆动质量以及有关的参量，就能求出摆盘系统的转动惯量。

设下圆盘质量为0m ，当它绕OO ＇扭转的最大角位移为o θ时，圆盘的中心位置升高h ，这时圆盘的动能全部转变为重力势能，有：gh m E P 0= （g 为重力加速度）当下盘重新回到平衡位置时，重心降到最低点，这时最大角速度为0ω，重力势能被全部转变为动能，有：式中0I 是下圆盘对于通过其重心且垂直于盘面的OO ‘轴的转动惯量。

如果忽略摩擦力，根据机械能守恒定律可得：200021ωI gh m =（1） 设悬线长度为l ，下圆盘悬线距圆心为R 0，当下圆盘转过一角度0θ时，从上圆盘B 点作下圆盘垂线，与升高h 前、后下圆盘分别交于C 和C 1，如图2所示，则：因为 22222)()()()(r R AC AB BC --=-= 所以 12102sin 4)cos 1(2BC BC Rr BC BC Rr h +=+-=θθ 在扭转角0θ很小，摆长l 很长时，sin22θθ≈，而BC+BC 1?2H ，其中H=22)(r R l --式中H 为上下两盘之间的垂直距离,则HRr h 220θ=（2）由于下盘的扭转角度0θ很小（一般在5度以内），摆动可看作是简谐振动。

三线摆法测定刚体的转动惯量一、实验简介转动惯量是刚体转动时惯性的量度，其量值取决于物体的形状、质量、质量分布及转轴的位置。

刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。

对于几何形状简单、质量分布均匀的刚体可以直接用公式计算出它相对于某一确定转轴的转动惯量。

对于任意刚体的转动惯量，通常是用实验方法测定出来的。

测定刚体转动惯量的方法很多，通常的有三线摆、扭摆、复摆等。

本实验要求学生掌握用三线摆测定物体转动惯量的方法,并验证转动惯量的平行轴定理。

二、实验原理图1三线摆结构示意图图2下圆盘的扭转振动1底座上的调平螺丝；3悬架和支杆连接的固定螺丝；5上圆盘悬线的固紧螺丝；7悬线；9待测金属环；当上、下圆盘水平时，将上圆盘绕竖直的中心轴线转动一个小角度,借助悬线的张力使悬挂的大圆盘绕中心轴作扭转摆动。

同时，下圆盘的质心将沿着转动轴升降，如上图中右图所示。

H是上、下圆盘中心的垂直距离；h 是下圆盘在振动时上升的高度；α是扭转角。

显然，扭转的过程也是圆盘势能与动能的转化过程。

扭转的周期与下圆盘（包括置于上面的刚体）的转动惯量有关。

当下圆盘的扭转角α很小时，下圆盘的振动可以看作理想的简谐振动。

其势能和动能分别为：（1）（2）式中是下圆盘的质量，g为重力加速度，h为下圆盘在振动时上升的高度，为圆频率，为下圆盘质心的速度，轴的转动惯量。

若忽略摩擦力的影响，则在重力场中机械能守恒：（3）因下圆盘的转动能远大于上下运动的平动能，于是近似有（4）又通过计算可得：（5）将（5）代入（4）并对t求导，可得：（6）该式为简谐振动方程，可得方程的解为：（7）因振动周期，代入上式得：故有：（8）由此可见，只要准确测出三线摆的有关参数、R、r、H 和，就可以精确地求出下圆盘的转动惯量。

如果要测定一个质量为m的物体的转动惯量，可先测定无负载时下圆盘的转动惯量，然后将物体放在下圆盘上，并注意，必须让待测物的质心恰好在仪器的转动轴线上。