两圆的公共弦(新高二)

过两圆交点的公共弦所在直线方程探究求经过两条曲线x 2+y 2+3x -y=0和3x 2+3y 2+2x+y=0交点的直线方程.常规解法是: 联立方程 ⎪⎩⎪⎨⎧=+++=-++)2(0233)1(032222y x y x y x y x求方程组解 )3(047)2(3)1(=--⨯y x 得 得代入即),1(,47x y = .137134;003134,0,0473164922112122⎪⎪⎩⎪⎪⎨⎧-=-=⎩⎨⎧==-===-++y x y x x x x x x x ），得分别代入（解得 即两交点坐标为 A(0,0), ).137,134(--B 过两交点的直线方程为 7x -4y=0. (4)由上面(1),(2)得到(3),这是解方程的基本步骤,我们可得以下结论结论1: 如果两条曲线方程是 f 1(x,y)=0 和 f 2(x,y)=0, 它们的交点是P(x 0,y 0),则方程 f 1(x,y)+λf 2(x,y)=0的曲线也经过P(x 0,y 0) (是任意常数).有了这个结论，有些题目可快速求解。

过两圆交点的公共弦所在直线方程就是将两圆方程联立消去二次项所得方程。

例2 (课本P70.13题) 求经过两圆x 2+y 2+6x -4=0和x 2+y 2+6y -28=0的交点,并且圆心在直线x -y -4=0上的圆的方程.解: 构造方程 x 2+y 2+6x -4+λ(x 2+y 2+6y -28)=0即 (1+λ)x 2+(1+λ)y 2+6x+6λy -(4+28λ)=0此方程的曲线是过已知两圆交点的圆,且圆心为)13,13(λλλ+-+-当该圆心在直线x -y -4=0上时,即 .7,041313-==-+++-λλλλ得 ∴ 所求圆方程为 x 2+y 2-x+7y -32=0例3：（P81.14题）求证：两椭圆b 2x 2+a 2y 2=a 2b 2, a 2x 2+b 2y 2=a 2b 2的交点在以原点为中心的圆周上，并求这个圆方程。

圆公共弦定理证明圆的十八个定理1、圆心角定理：在同圆或等圆中，相等的圆心角所对弧相等，所对的弦相等，所对的弦的弦心距相等。

推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2、圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等推论2：半圆（或直径）所对的圆周角是直角；90°的圆周角所推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形3、垂径定理：垂直弦的直径平分该弦，并且平分这条弦所对的两条弧。

推论1：①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧推论2：圆的两条平行弦所夹的弧相等4、切线之判定定理：经过半径的外端并且垂直于该半径的直线是圆的切线。

5、切线长定理：从圆外一点引圆的两条切线，他们的切线长相等，这一点与圆心的连线平分这两条切线的夹角。

6、公切线长定理：如果两圆有两条外公切线或两条内公切线，那么这两条外公切线长相等，两条内公切线长也相等。

如果他们相交，那么交点一定在两圆的连心线上。

7、相交弦定理：圆内两条弦相交，被交点分成的两条线段长的乘积相等。

8、切割线定理：从圆外一点向圆引一条切线和一条割线，则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。

9、割线长定理：从圆外一点向圆引两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

10、切线的性质定理：圆的切线垂直于经过切点的半径推论1：经过圆心且垂直于切线的直线必经过切点推论2：经过切点且垂直于切线的直线必经过圆心11、弦切角定理：弦切角等于它所夹的弧对的圆周角推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等12、定理：相交两圆的连心线垂直平分两圆的公共弦13、定理：把圆分成n（n≥3）：（1）依次连结各分点所得的多边形是这个圆的内接正n边形2）经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形14、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆15、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆16、定理：正n边形的半径和边心距把正n边形分成2n个全等的直角三角形17、定理：圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。

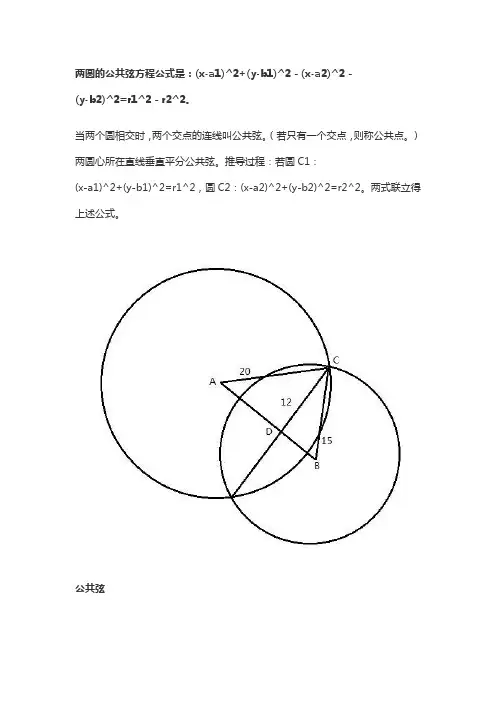
两圆的公共弦方程公式是：(x-a1)^2+(y-b1)^2－(x-a2)^2－
(y-b2)^2=r1^2－r2^2。

当两个圆相交时，两个交点的连线叫公共弦。

（若只有一个交点，则称公共点。

）两圆心所在直线垂直平分公共弦。

推导过程：若圆C1：
(x-a1)^2+(y-b1)^2=r1^2，圆C2：(x-a2)^2+(y-b2)^2=r2^2。

两式联立得上述公式。

公共弦
两个圆若是相交，则至多交于2点。

而将两圆的方程相减即是默认两条方程中有共同的解X、Y。

而减后的方程必定满足X、Y（就是两个交点），换句话说，就是两个交点所共同满足的直线方程。

而我们知道，平面内2点间有且只有1条直线，那么这条直线就是所求的公共弦。

设两圆分别为：x^2+y^2+c1x+d1y+e1=0。

x^2+y^2+c2x+d2y+e2=0。

两式相减得：（x^2+y^2+c1x+d1y+e1）-（x^2+y^2+c2x+d2y+e2）=0。

这是一条直线的方程。

两圆的公共弦的简易求法作者：魏道勇来源：《新一代》2011年第04期摘要：圆锥曲线中求两圆的公共弦，寻求更有效解题方法。

避免了大量的，繁琐的代数运算，节省了做题时间，提高了准确率。

关键词：圆锥曲线；公共弦；简易求法中图分类号：G630文献标识码：A文章编号：1003-2851（2011）04-0141-01圆锥曲线中求两圆的公共弦常用联立两圆的方程，消去x2与y2项后得关于x,y的一次方程，即公共弦所在的直线方程的方法解之。

例如：求圆x2+y2=4与圆x2+y2+4x-4y-1=0公共弦所在的直线的方程同学们易联立两个方程，解出两个交点坐标，然后根据两点求出所要的公共弦的方程，显然这样做需要花费大量的运算时间，虽然做出来了，可以说是事倍功半。

实际上两个方程联立相减消去x2与y2项，即(x2+y2-4)-(x2+y2+4x-4y-1)=0化简即得公共弦的方程为：4x-4y+3=0。

另外，我们在圆锥曲线中常遇到有关中点弦所在的直线方程的问题，学生习惯用设斜率k，写出直线方程与圆锥曲线方程联立，表示中点，求出k，再写出直线方程，这样虽可行，但运算量太大，易出错，现在让我们大胆联想用圆中的方法可否解决。

若圆锥曲线C的方程为：f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F=0点M(m,n)是曲线C的弦PQ的中点，我们来求弦PQ所在的直线的方程。

分析：如何构造出两个相似的方程呢？我们知道弦的两个端点都在曲线上，且关于中点对称，端点的坐标满足方程，这样可构造两个方程。

让我们试一试。

设P的坐标为(x,y)，则Q的坐标为(2m-x,2n-y)，PQ两点都满足曲线C的方程即有f(x,y)=0f(2m-x,2n-y)=0亦即Ax2+Bxy+Cy2+Dx+Ey+F=0A(2m-x)2+B((2m-x)(2n-y)+C(2n-y)2+D(2m-x)+E(2n-y)+F=0两式相减得:f(x,y)-f(2m-x,2n-y)=0，即得：(2mA+nB+D)x+(mB+2nC+E)y-(2m2A+2mnB+2n2C+Dm+En)=0*当2mA+nB+D与mB+2nC+E不同时为零时，上式方程表示是直线，它是不是弦PQ所在直线的方程呢？显然P的坐标满足*式，也易验证点M(m,n)满足*式方程，又两点确定一条直线，故*式方程可看作是P,M确定的直线方程，也就是弦PQ所在直线的方程。

两圆公共弦所在直线方程与切线长相等四川省筠连县中学邓敬过圆和圆交点的圆系方程：（为参数，且）.当时，上式可化为过两圆公共弦所在直线方程：【实质】：将两圆方程相减可得两圆公共弦所在直线方程.下面介绍几个有关公共弦所在直线方程的重要结论，并举例运用，以加深学生对其该知识点的理解和掌握.1.若两圆相交，则方程为它们公共弦所在直线方程.【例1】：（新课标人教版A必修二，P133，习题4.2，A组9题）求圆与圆的公共弦长.【解析】：设两圆交于两点，将两圆方程相减可得公共弦所在直线方程：.再由再由弦长公式得：.当然，此题解法很多，该解法重点体现两圆公共弦所在直线方程的应用，其他解法在这里就不再遨述.同题型还有（新课标人教版A必修二，P144，复习参考题A组4题）求圆与圆的公共弦长.此题解答可参照例1.2.两圆外一动点P，向两相交圆所引切线长相等，则方程是P点的轨迹方程.【例2-1】：圆与圆外一动点P，向两圆所引切线长相等，则动点P的轨迹方程为【解析】：由切线长定理可知：所以P在两圆的公共弦所在直线上.即P点的轨迹为（P在两圆外）.【例2-2】：已知和，在平面上找一点P，过P点引两圆切线并使他们的长都等于.【说明】：圆外一点，则向圆引切线长满足：.【解析】：如图所示，P点是两圆公共弦所在直线与以（或）为圆心，以（或）为半径的圆的交点.∴设，依题意可得：或∴P的坐标是或.【例2-3】：（新课标人教版A必修二，P144，复习参考题，A组6题），已知圆和圆关于直线对称，求直线方程.【解析】：由题意可知两圆相交，对称轴是两圆的中垂线.将两圆方程相减可得到其对称轴方程：.3.一动点P，向两相外切的圆所引切线长相等，则方程是P点的轨迹方程.【例3】：已知与相外切，两圆外一动点P，向两圆所引切线长相等，则P点的轨迹方程.【解析】：如图所示，，∴P点的轨迹方程仍为两圆方程之差,即为：.4.一动点P，向两相外离的圆所引切线长相等，则方程是P点的轨迹方程.两圆外离是将相交两圆的圆心距扩大所致，所以可以进行类比推理.【例4-1】：（07四川理15）、已知的方程是，的方程是，由动点向和所引的切线长相等，则动点的轨迹方程是【解析】：：圆心，半径；：圆心，半径．两圆外离.动点的轨迹由两圆方程相减可得：．【例4-2】：（新课标人教版A必修二，P144，复习参考题A组7题）求与圆关于直线对称的圆的方程.【注意】：圆C和直线是相外离，所以对称后的两圆位置关系是外离，但是由于与已知圆共弦的圆不能唯一确定，所以通过类比此题不能用公共弦所在直线方程的思路来处理.【解析】：圆C圆心（），，设所求圆方程为，直线是两圆连心线的垂直平分线.∴∴所求圆的方程为.同类型的题还有（新课标人教版A必修二，P133，习题4.2，A组7题），求与圆C：关于直线L:对称的圆的方程.同学们可以参照例题4-2求解.。

弦长公式在相交两圆中的运用-CAL-FENGHAI.-(YICAI)-Company One1弦长公式在相交两圆中的运用重庆市永川区第六中学校 潘祥万（402182）问题：求两圆04026,010102222=-+++=--+y x y x y x y x 的公共弦的长。

（高二数学（上），人教版，P 88 24题）对于此题，我们很多时候都是把这两个方程联立组成方程组，求出其交点坐标，再根据两点间的距离公式求解，这是一种常规解法。

下面，我想就相交两圆公共弦长公式的推导及运用谈点个人看法。

一、弦长公式的推导在初中，我们就知道两圆相交时弦长的求法。

对于高中数学中的相交两圆弦长如何求，大部分学生感到不知所措，甚至解题的方向也把握不准，基于此，我在教学中，我在引领学生回忆初中知识的同时，让学生把所学的知识在头脑中重组、建构，形成一定的网络，更好地为教学服务。

推导：对于圆的一般方程：022=++++F Ey Dx y x （其中0422>-+F E D ）和圆的标准方程：222)()(R b y a x =-+-。

这是我们应该熟悉的两个方程，要求学生必须能够互化。

如果两圆222)()(r b y a x =-+-和222)()(R b y a x ='-+'-相交，求公共弦长。

在这里必须引导学生对问题进行分析，看它圆心在弦的同旁，还是两旁。

（一）、两圆心在公共弦的两旁时，公共弦长AB 的求法如图1：设相交两圆的圆心分别为O ),(b a ,),(b a O ''',半径分别为R r ,,圆心距(O O ')为d ,则在Rt △ACO 与Rt △AC O '中有222222,AC O A C O OC AO AC -'='-=,又O O '=OC+C O '=d ,∴C O '=d -OC,∴222222)(,AC R OC d OC r AC -=--=,∴22222)(AC R AC r d -=--,其中22)()(b b a a d -'+-'=图1化简得:AB=2AC=[][]d r R d d r R 2222)()(---+ )(r R ≥ ① (二)、两圆心在公共弦的同旁时，公共弦长AB 的求法如右图，设相交两圆的圆心分别为O ),(b a ,),(b a O ''',半径分别为)(,r R R r ≥,圆心距(O O ')为d （22)()(b b a a d -'+-'=）,则在Rt △ACO 与Rt △AC O '中，同理得： [][]d r d R R r d AB 2222)()(---+= ② 说明：内切、外切时上两式也成立，只不过AB=0。

两个圆相交的公共弦方程推导过程1.假设有两个相交的圆。

Assume there are two intersecting circles.2.圆的方程式为(x - h1)^2 + (y - k1)^2 = r1^2和(x - h2)^2 + (y - k2)^2 = r2^2。

The equations of the circles are (x - h1)^2 + (y - k1)^2 = r1^2 and (x - h2)^2 + (y - k2)^2 = r2^2.3.假设两个圆相交于点A和点B。

Suppose the two circles intersect at points A and B.4.点A和点B有相同的坐标(x, y)。

Points A and B have the same coordinates (x, y).5.因此，点A和点B的坐标都满足圆的方程式。

Therefore, the coordinates of points A and B satisfy the equations of the circles.6.将点A的坐标代入两个圆的方程式，得到以下方程式：(x -h1)^2 + (y - k1)^2 = r1^2和(x - h2)^2 + (y - k2)^2 = r2^2。

Substituting the coordinates of point A into the equations of the circles, we get the following equations: (x - h1)^2 + (y - k1)^2 = r1^2 and (x - h2)^2 + (y - k2)^2 =r2^2.7.将点B的坐标代入两个圆的方程式，得到以下方程式：(x -h1)^2 + (y - k1)^2 = r1^2和(x - h2)^2 + (y - k2)^2 = r2^2。

相交圆的公共弦方程推导哎呀，说到相交圆的公共弦方程，这可是一件既有趣又神秘的事情，感觉就像在探索宇宙中的某个秘密。

圆圈，咱们平常见得多，乍一看，它们好像就是一些简单的图形，没啥特别的。

但实际上，圆圈里藏着不少故事哦，就像咱们身边的人，有时候你不去深入了解，它们的精彩只会悄悄溜走。

想象一下，有两个圆圈，在平面上优雅地交错着，正如朋友们在一起聚会，欢声笑语，不同的背景，却能碰撞出有趣的火花。

这就是相交圆，它们不仅仅是图形，更是数学的浪漫。

公共弦是什么呢？简单来说，就是那条把两个圆连接起来的线，就像是一条纽带，把它们的心紧紧相连，仿佛在说：“嘿，我们是朋友，要一起走下去！”可别小看这条线，它可承载了许多秘密。

就像你和朋友之间的共同经历，越多越深厚。

想象一下，两个圆圈相交，形成的公共弦就是它们之间最美的回忆。

咱们就来聊聊怎么推导出这条公共弦的方程吧，保证让你轻松get到这个数学小秘密。

咱们得把两个圆圈的方程拿出来晃一晃，想象它们像两位老朋友，互相打招呼。

第一个圆的方程是 ((x x_1)^2 + (y y_1)^2 = r_1^2)，第二个圆的方程是 ((x x_2)^2 + (yy_2)^2 = r_2^2)。

哇，这个看起来有点复杂，不过别担心，慢慢来。

咱们可以把这两个方程展开，就像拆开礼物一样，兴奋又期待。

展开之后，你会发现它们其实有很多相似之处，简直就像是双胞胎兄弟，虽然长得差不多，但心里都藏着各自的故事。

咱们可以把其中一个方程减去另一个方程，这样就能消掉一些不必要的东西，留下的东西就简单多了。

你看，数学不就是这么好玩嘛！当你把两个方程结合在一起，解出来后，会得到一个关于 (x) 和 (y) 的方程。

这时候，哇哦，奇迹发生了，咱们已经找到了这条公共弦的方程！就像是朋友们聚在一起，找到了共同话题，聊得不亦乐乎。

哦，对了，推导过程中别忘了要保持耐心，数学就像是养花，慢慢来，才能收获美丽的花朵。

如果中途有点困难，也没关系，大家都有这样的经历。

两个圆的公共弦方程推导## English Answer: ##。

Let $(x h_1)^2 + (y k_1)^2 = r_1^2$ and $(x h_2)^2 + (y k_2)^2 = r_2^2$ be the equations of two circles with centers $(h_1, k_1)$ and $(h_2, k_2)$, respectively, and radii $r_1$ and $r_2$, respectively. Let the circles intersect at points $A$ and $B$.The distance between the centers of the circles is given by.$$d = \sqrt{(h_1 h_2)^2 + (k_1 k_2)^2}.$$。

The length of the common chord $AB$ is given by.$$|AB| = 2\sqrt{r_1^2 \left(\frac{d}{2}\right)^2} =2\sqrt{r_2^2 \left(\frac{d}{2}\right)^2}.$$。

The midpoint of the common chord $AB$ is the point.$$\left(\frac{h_1 + h_2}{2}, \frac{k_1 +k_2}{2}\right).$$。

The slope of the common chord $AB$ is given by.$$m = \frac{k_1 k_2}{h_1 h_2}.$$。

The equation of the common chord $AB$ can be written in point-slope form as.$$y \frac{k_1 + k_2}{2} = m\left(x \frac{h_1 +h_2}{2}\right).$$。

高二春季 数学“圆的弦、切线、与最值问题”学生姓名 授课日期 教师姓名授课时长圆是数学中优美的图形，具有丰富的性质．由于其图形的对称性和完美性，很多与圆有关的最值问题都可以运用圆的图形性质，利用数形结合求解．当然，根据《教学要求》的说明，“平面解析几何的重要内容，教学重点是让学生从中感受运用代数方法处理几何问题的思想”，因此在此类问题的求解中，有时也会用到函数思想和基本不等式思想等．本文将就与圆的弦、切线、与最值问题有关的题目进行归纳总结，希望能为学生在处理此类问题时提供帮助。

1、在标准方程222)()r b y a x =-+-（下过圆上一点),00y x P （的切线方程为：200))(())r b y b y a x a x =--+--（（ ；在一般方程022=++++F Ey Dx y x （0422>-+F E D ） 下过圆上一点),00y x P （的切线方程为：0220000=++++++F y y E x x Dyy xx 。

2、两相交圆011122=++++F y E x D y x （0412121>-+F E D ）与022222=++++F y E x D y x（0422222>-+F E D ） 的公共弦所在的直线方程为：0)()()(212121=-+-+-F F y E E x D D 。

3、过圆022=++++F Ey Dx y x （0422>-+F E D ）外一点),11y x P （作圆的切线，其切线长公式为：F Ey Dx y x PA ++++=112121||。

4、过圆022=++++F Ey Dx y x （0422>-+F E D ）外一点),11y x P （作圆的切线，切点弦AB所在直线的方程为：211))(())r b y b y a x a x =--+--（（（在圆的标准方程下的形式）； 0221111=++++++F y y E x x D yy xx （在圆的一般方程下的形式）。

两圆的公共弦和圆心连线关系嘿，各位小伙伴，今天咱们来聊聊那个老生常谈却又让人头疼的问题——如何理解两个圆相交时，它们之间的那条“神秘”的公共弦以及这条弦与圆心的关系。

咱们得用点生活化的语言，把复杂的数学公式变成大家一听就懂的故事。

想象一下，你手里拿着一张地图，上面画着两个圆圆滚滚的地标。

这两个地标就像是两个好朋友，它们之间有一条看不见的线，这就是它们的“共同弦”。

这条弦就像是它们的友谊纽带，连接着它们，让它们在空间里相遇、相知、相伴。

咱们先说说这条弦是什么玩意儿。

它可不是随便一条线，而是两条圆弧的交点连起来的。

想象一下，如果把这两条圆弧比作是两条道路，那么这条弦就是它们交汇的地方。

这就好比是你和朋友约定了见面的时间和地点，然后你们在路上相遇了。

现在，咱们再来看看这条弦和圆心有什么关系。

这条弦就像是你们的见面礼，它的长度和位置都代表着你们友谊的深浅和长度。

如果这条弦离圆心越远，那说明你们之间的关系就越亲密；如果这条弦离圆心越近，那说明你们之间的关系就越疏远。

举个例子来说吧，假设有两个圆圆心，它们之间的距离是10个单位长度。

当这条公共弦从圆心出发，穿过这两个圆圆心时，它的最短路径就是20个单位长度。

这个20单位长度，就是我们说的这条弦的长度。

这条弦的位置呢？它就像是一个坐标系里的点，告诉你这条弦是在圆心的哪个方向上。

当然了，这只是一个简单的比喻。

在现实生活中，我们处理问题时，往往需要更复杂、更精细的分析方法。

但在这个问题上，我们可以用简单的线条和坐标来形象地描述这个问题。

所以啊，小伙伴们，当我们遇到类似的问题时，不妨用这种简单明了的方式来分析。

这样既能帮助我们更好地理解问题，又能让我们的思维变得更加灵活和有趣。

两圆相交时，他们的公共弦和圆心连线关系就像是一段美丽的友谊故事。

只要我们用心去感受，就能发现其中的美好和智慧。

好了，今天的分享就到这里，希望大家都能在生活中找到属于自己的那份美好和智慧。

圆的公共弦圆是自然界中最完美的形状，它在许多地方都有所体现，比如太阳、月亮、钟、环、果实等等。

人们经常将它用来象征完美、爱心和归属感，有着深远的文化内涵。

同时，圆也是许多建筑、机械及艺术作品中常见的组成部分。

圆也有许多个性化的含义，可以帮助我们理解世界和自我。

对于艺术家而言，圆形正是他们创作的灵感来源，可以表现出美好、灵动、和谐、安稳等艺术感受。

圆型也是许多反映自然规律的数学概念的象征，通过它可以表达宇宙的一切理性思想。

圆的公共弦（circumcircle）是一个重要的数学概念，它主要用来描述多边形的公共弦线。

公共弦是指一组多边形上的邻点共同组成的弦线，也就是说两个邻点都有该弦线。

圆的公共弦是指在多边形的每个顶点到其他顶点的端点之间的弦线，组成了一个圆。

圆的公共弦有许多应用，比如建筑设计、机械结构、电子产品等等。

在建筑设计中，它主要被用来描述弧形结构，例如墙体等。

而在机械结构的设计中，它也被广泛用于描述某些零件的外形，比如管道。

此外，圆的公共弦还被广泛应用于室内设计，比如设计圆柱形、弧形等墙面装饰或物品陈列。

圆的公共弦不仅仅有实际用途，它也是一个重要的文化符号。

圆形的结构具有秩序性、协调性、完整性等特点，它表达着宇宙的真理，强调了宇宙间的一致性，同时也与和谐、安宁和无穷有着深刻的联系。

因此，圆的公共弦在许多领域都有着重要的意义，可以用来象征完美、爱心和归属感。

圆的公共弦的科学研究仍处于初级阶段，但已经取得了一些成果。

研究发现，圆的公共弦可以帮助人们更好地理解形体的外型，同时也可以帮助人们理解艺术、科学、文化等方面的思想，因此，圆的公共弦具有着重要的科学价值。

总之,的公共弦是一个重要的数学概念，它在实际应用和文化研究中都有着重要作用。

它象征着宇宙真理，强调了和谐、安宁与无穷。

圆的公共弦可以帮助人们更好地理解形体的外型，同时也可以帮助人们理解艺术、科学、文化等方面的思想，因此，圆的公共弦具有着重要的科学价值。