两圆相交公共弦 常用辅助线作法

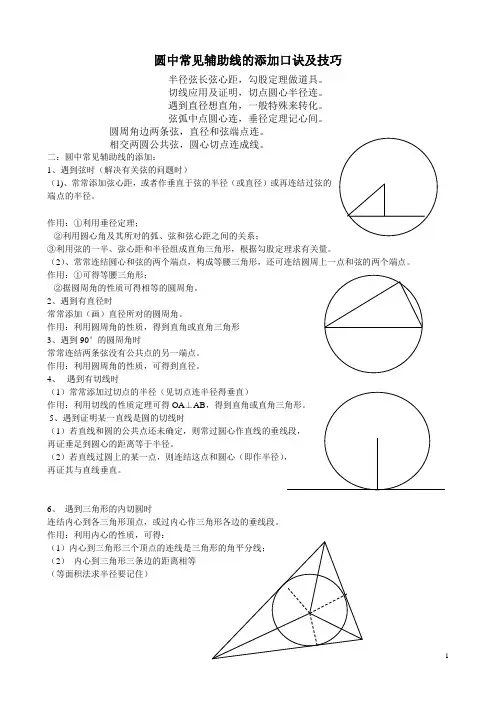
圆中常见辅助线的添加口诀及技巧半径弦长弦心距，勾股定理做道具。

切线应用及证明，切点圆心半径连。

遇到直径想直角，一般特殊来转化。

弦弧中点圆心连，垂径定理记心间。

圆周角边两条弦，直径和弦端点连。

相交两圆公共弦，圆心切点连成线。

二：圆中常见辅助线的添加：1、遇到弦时（解决有关弦的问题时）（1)、常常添加弦心距，或者作垂直于弦的半径（或直径）或再连结过弦的端点的半径。

作用：①利用垂径定理；②利用圆心角及其所对的弧、弦和弦心距之间的关系；③利用弦的一半、弦心距和半径组成直角三角形，根据勾股定理求有关量。

（2）、常常连结圆心和弦的两个端点，构成等腰三角形，还可连结圆周上一点和弦的两个端点。

作用：①可得等腰三角形；②据圆周角的性质可得相等的圆周角。

2、遇到有直径时常常添加（画）直径所对的圆周角。

作用：利用圆周角的性质，得到直角或直角三角形3、遇到90°的圆周角时常常连结两条弦没有公共点的另一端点。

作用：利用圆周角的性质，可得到直径。

4、遇到有切线时（1）常常添加过切点的半径（见切点连半径得垂直）作用：利用切线的性质定理可得OA⊥AB5、遇到证明某一直线是圆的切线时（1再证垂足到圆心的距离等于半径。

（2再证其与直线垂直。

6、遇到三角形的内切圆时连结内心到各三角形顶点，或过内心作三角形各边的垂线段。

作用：利用内心的性质，可得：（1（2）内心到三角形三条边的距离相等（等面积法求半径要记住）7、作用：外心到三角形各顶点的距离相等。

例题1、如图，已知△ABC内接于⊙O，∠A=45°，BC=2，求⊙O的面积。

例题2、如图，弦AB的长等于⊙O的半径，点C在弧AMB上，则∠C的度数是________.例题3、如图，AB是⊙O的直径，AB=4，弦BC=2,∠B=例题4、如图，AB、AC是⊙O的的两条弦，∠BAC=90°，AB=6，AC=8，⊙O的半径是例题5、如图所示，已知AB是⊙O的直径，AC⊥L于C，BD⊥L于D，且AC+BD=AB。

初中数学试卷马鸣风萧萧例谈圆中常见作辅助线的方法圆是初中几何部分的重要内容之一，与圆有关的大部分几何题型都需要添加辅助线来解决。

只要添上合适的辅助线，不仅会使问题迎刃而解，而且还会有效地培养学生的解题能力与创造性思维能力。

通过对实践教学中的归纳与总结，发现添加辅助线的方法有很多，本文就圆中常见作辅助线的方法归纳如下：一、作弦心距——在与弦有关的计算或证明题时，常作辅助线的方法是作弦心距例1 如图1，AB 为⊙Ｏ的直径，PQ 切⊙Ｏ于T ，AC ⊥PQ 于C ，交⊙Ｏ于D ，AD=2，TC=3.求⊙Ｏ的半径。

解：过点O 作OM ⊥AC 于M ，∴AM=MD=AD/2=1.∵PQ 切⊙Ｏ于T ，∴OT ⊥PQ ．又∵AC ⊥PQ ，OM ⊥AC ， ∴∠OTC=∠ACT=∠OMC=90°， ∴四边形OTCM 为矩形．∴OM=TC=3， ∴在Rt △AOM中，2AO =． 即⊙Ｏ的半径为2．例2 如图2，已知在以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于C 、D 两点. 求证：AC=BD.证明：过点O 作OE ⊥AB 于E ，则AE=BE ，CE=DE ，∴AE-CE=BE-DE. ∵AC=AE-CE ，BD=BE-DE. ∴AC=BD.二、连半径——与半径和弦有关的简单计算、已知圆中有切线的有关计算和证明时，常作辅助线的方法是连半径例3 如图3，⊙O 的直径CD=20cm ，直线l ⊥CO ，垂足为H ，交⊙O 于A 、B 两点，AB=16 cm ，直线l 平移多少厘米时能于⊙O 相切？ 解：连接OA ，· Ｃ Ｄ ＡＥ ＢＯ图2A 图1M∵l ⊥CO ，∴OC 平分AB ∴AH=8cm.在Rt △AHO 中，OH==-=-2222810AH AO 6cm. ∴CH=4cm ，DH=16 cm.答：直线l 向左平移4cm ，或向右平移16cm 时能于⊙O 相切。

例4 如图4，PA 是⊙O 的切线，切点是A ，过点A 作AH ⊥OP 于点H ，交⊙O 于点B. 求证：PB 是⊙O 的切线. 证明：连接OA 、OB.∵PA 是⊙O 的切线，∴∠OAP=90°. ∵OA=OB ，AB ⊥OP ，∴∠AOP=∠BOP. 又∵OA=OB ，OP=OP ，∴△AOP ≌△BOP. ∴∠OPB=∠OAP=90°. ∴PB 是⊙O 的切线.三、既作弦心距又连半径——与半径和弦都有关的计算时，常作辅助线的方法是既作弦心距又连半径，利用勾股定理来解决例5 直径为52厘米的圆柱形油槽内装入一些油后，截面如图5，若油最大深度为16厘米.那么油面宽度AB 的长是多少厘米？解：连接OA ，作OC ⊥AB 于C ，则AC=BC=21AB.在Rt △OAC 中，OA=21×52=26厘米，OC=26-16=10厘米，∴AC==-=-22221026OC OA 24厘米.∴AB=2AC=48厘米.四、连弦构造相似三角形或直角三角形——在圆中与弦或其他有关的计算或证明时，常作辅助线的方法是连弦，利用同弧所对的圆周角相等连弦构造相似三角形或利用直径所对的圆周角为直角这个性质连弦构造出直角三角形，从而将问题转化到相似三角形或直角三角形中去计算或证明例6 已知，如图6，在半径为4的⊙O 中，AB ，CD 是两条直径，M 为OB 的中点，CM的延长线交⊙O 于点E ，且EM ＞MC ．连结DE ，（1）求证：AM ·MB=EM ·MC ； （2）求EM 的长； （3）求sin ∠EOB 的值.解：（1）连接AC ，EB ，则∠CAM=∠BEM.又∠AMC=∠EMB, ∴△AMC ∽△EMB ．∴ EM MBAM MC =，即AM ·MB=EM ·MC ． （2）∵DC 为⊙O 的直径，A 图 4· BPOH A BO·图5C B图6∴∠DEC=90°，EC=7.== ∵OA=OB=4，M 为OB 的中点，∴AM=6，BM=2．设EM=x ，则CM=7－x ．代入（1）,得 62(7)x x ⨯=-.解得1x =3，2x =4．但EM ＞MC ，∴EM=4.（3）由（2）知，OE=EM=4，作EF ⊥OB 于F ，则OF=MF=41OB=1．在Rt △EOF 中，,15142222=-=-=OF OE EF∴sin ∠EOB =415=OE EF . 例7 如图7所示，△ABC 是直角三角形，∠ABC=90°，以AB 为直径的⊙O 交AC 于点E ，点D 是BC边的中点，连结DE ． （1）求证：DE 与⊙O 相切；（2）若⊙O DE=3，求AE ． （1）证明：连结OE ，BE ，∵AB 是直径，∴BE ⊥AC. ∵D 是BC 的中点， ∴DE=DB ， ∴∠DBE=∠DEB.又OE=OB ， ∴∠OBE=∠OEB ， ∴∠DBE+∠OBE=∠DBE+∠OEB. 即∠ABD=∠OED.又∵∠ABC=90°，∴∠OED=90°， ∴DE 是⊙O 的切线.（2）解：∵346)32(2222=+=+=BC AB AC ，∴334632=⨯=⋅=AC BC AB BE ，∴33)32(2222=-=-=BE AB AE .五、作直径构造直角三角形——在圆中牵涉到三角函数的运算或与直径的计算与证明时，常作辅助线的方法是作直径，利用直径所对的圆周角是直角构造直角三角形，从而将问题转化到直角三角形中去解决例8 如图8, 点A 、B 、C 在⊙O 上（AC 不过O 点），若∠ACB=60°,AB=6，求⊙O 半径的长。

解题技巧专题圆中辅助线的作法在解题过程中，我们经常会遇到一些问题，例如如何构造等腰三角形、正方形、平行四边形等几何图形，以及如何构造垂直线、角平分线、中位线等几何线段。

这些问题在解决数学问题时非常常见，而圆中辅助线的作法就是一种常用的解决这类问题的技巧。

圆中辅助线的作法是指在解决圆相关的问题时，通过添加一些辅助线来辅助解决问题。

这些辅助线可以增强我们对图形的理解，简化问题的分析过程，使问题更易于解决。

下面将介绍一些常见的圆中辅助线的作法：1.构造圆的切线如果需要构造一条圆的切线，可以先连接圆心与切点，然后再从切点向圆外引一条与半径垂直的线段，两条线段的交点就是切线的切点。

利用这条切线可以帮助我们解决一些关于切线的性质问题。

2.构造垂直线如果需要构造一条与圆上特定点垂直的直线，可以连接该点与圆心，并在圆上引一条经过该点的切线，然后从圆心引一条与切线垂直的线段，两条线段的交点就是所求直线与圆的交点。

利用这条直线可以帮助我们解决一些关于圆的性质问题。

3.构造角平分线如果需要构造一条角的平分线，可以先连接角的两个顶点与圆心，然后再从圆心引一条与角平分线相垂直的线段，两条线段的交点就是所求角的平分线与圆的交点。

利用这条角平分线可以帮助我们解决一些关于角平分线的性质问题。

4.构造中位线如果需要构造一条线段的中位线，可以将线段的两个端点连接到圆心，并在圆上引一条经过中点的切线，然后再从圆心引一条与切线垂直的线段，两条线段的交点就是所求线段的中点。

利用这条中位线可以帮助我们解决一些关于线段中点的性质问题。

5.构造等腰三角形如果需要构造一个等腰三角形，可以先在圆上确定一个顶点，然后连接圆心与该点，并延长线段到圆的另一侧，再将圆切割成两个等弧，然后以切割点为顶点连接圆心，就可以得到一个等腰三角形。

利用这个等腰三角形可以帮助我们解决一些关于等腰三角形的性质问题。

这些是一些常见的圆中辅助线的作法，通过添加这些辅助线，我们可以更好地理解和解决与圆相关的问题。

1． 遇到弦时（解决有关弦的问题时）常常添加弦心距，或者作垂直于弦的半径（或直径）或再连结过弦的端点的半径。

或者连结圆心和弦的两个端点，构成等腰三角形，还可连结圆周上一点和弦的两个端点。

作用：1、利用垂径定理；2、利用圆心角及其所对的弧、弦和弦心距之间的关系；3、利用弦的一半、弦心距和半径组成直角三角形，根据勾股定理求有关量。

4、可得等腰三角形；5、据圆周角的性质可得相等的圆周角。

例：如图，ＡＢ是⊙O 的直径,PO ⊥AB 交⊙O 于P 点，弦PN 与AB 相交于点M ， 求证：PM •PN=2PO 2.分析：要证明PM •PN=2PO 2，即证明PM •PC =PO 2，过O 点作OC ⊥PN 于C ，根据垂经定理 NC=PC ，只需证明PM •PC=PO 2，要证明PM •PC=PO 2只需证明Rt △POC ∽Rt △PMO. 证明: 过圆心O 作OC ⊥PN 于C ，∴PC=21PN ∵PO ⊥AB, OC ⊥PN ，∴∠MOP=∠OCP=90°. 又∵∠OPC=∠MPO ，∴Rt △POC ∽Rt △PMO. ∴PO PC PM PO即∴PO 2= PM •PC. ∴PO 2= PM •21PN ，∴PM •PN=2PO 2. 【例1】如图，已知△ABC 内接于⊙O ，∠A=45°，BC=2，求⊙O 的面积。

【例2】如图，⊙O 的直径为10，弦AB ＝8，P 是弦AB 上一个动点，那么OP 的长的取值范围是_________．【例3】如图，弦AB 的长等于⊙O 的半径，点C 在弧AMB 上，则∠C 的度数是________.CBBA2． 遇到有直径时常常添加（画）直径所对的圆周角。

作用：利用圆周角的性质，得到直角或直角三角形。

例 如图，在△ABC 中，∠C=90°，以BC 上一点O 为圆心，以OB 为半径的圆交AB 于点M ，交BC 于点N ．（1） 求证：BA ·BM=BC ·BN ；（2） 如果CM 是⊙O 的切线，N 为OC 的中点，当AC=3时，求AB 的值．分析：要证BA ·BM=BC ·BN ，需证△ACB ∽△NMB ，而∠C=90°，所以需要△NMB 中有个直角，而BN 是圆O 的直径，所以连结MN 可得∠BMN=90（1） 证明：连结MN ，则∠BMN=90°=∠ACB ∴△ACB ∽△NMB ∴BNAB BMBC∴AB ·BM=BC ·BN（2） 解：连结OM ，则∠OMC=90° ∵N 为OC 中点∴MN=ON=OM ，∴∠MON=60° ∵OM=OB ，∴∠B=21∠MON=30° ∵∠ACB=90°，∴AB=2AC=2×3=6【例4】如图，AB 是⊙O 的直径，AB=4，弦BC=2,∠B=3． 遇到90°的圆周角时常常连结两条弦没有公共点的另一端点。

圆中常见辅助线的做法一．遇到弦时（解决有关弦的问题时）1.常常添加弦心距，或作垂直于弦的半径（或直径）或再连结过弦的端点的半径.作用：①利用垂径定理；②利用圆心角及其所对的弧、弦和弦心距之间的关系；③利用弦的一半、弦心距和半径组成直角三角形,根据勾股定理求有关量。

例：如图,在以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于C 、D 二点。

求证：AC = BD证明:过O 作OE ⊥AB 于E∵O 为圆心，OE ⊥AB∴AE = BE CE = DE∴AC = BD练习：如图,AB 为⊙O 的弦,P 是AB 上的一点，AB = 10cm,PA = 4cm 。

求⊙O 的半径。

2.有等弧或证弧等时常连等弧所对的弦或作等弧所对的圆心角.例：如图，已知AB 是⊙O 的直径，M 、N 分别是AO 、BO 的中点，CM ⊥AB ，DN ⊥AB ，求证: AC BD = 证明：（一）连结OC 、OD∵M 、N 分别是AO 、BO 的中点∴OM =12AO 、ON = 12BO ∵OA = OB ∴OM = ON∵CM ⊥OA 、DN ⊥OB 、OC = OD ∴Rt △COM ≌Rt △DON ∴∠COA = ∠DOB ∴AC BD =(二）连结AC 、OC 、OD 、BD∵M 、N 分别是AO 、BO 的中点 ∴AC = OC BD = OD∵OC = OD ∴AC = BD ∴AC BD =3.有弦中点时常连弦心距例：如图，已知M 、N 分别是⊙O 的弦AB 、CD 的中点，AB = CD ，求证：∠AMN = ∠CNM证明:连结OM 、ON∵O 为圆心，M 、N 分别是弦AB 、CD 的中点∴OM ⊥AB ON ⊥CD ∵AB = CD ∴OM = ON ∴∠OMN = ∠ONM∵∠AMN = 90o－∠OMN ∠CNM = 90o －∠ONM∴∠AMN =∠CNM4.证明弦相等或已知弦相等时常作弦心距。

两圆相交公共弦常用辅助线作法教学目标：1、深刻理解相交两圆的性质，并能初步运用它解决有关问题。

2、掌握辅助线做法的规律。

教学重点：两圆相交的性质及勾股定理的应用教学难点：灵活的运用口诀添加辅助线。

教学过程：我今天讲的是有关两圆相交公共弦常用辅助线的做法。

例：如图1，半径为5的两个等圆⊙O1与⊙O2相交于A、B，公共弦AB=8．由点O1向⊙O2作切线O1C，切点为C，则O1C的长为图1 图2分析：本题主要考查相交两圆的性质和圆与圆的位置关系的知识点，此题要综合运用相交两圆的性质、切线的性质定理和勾股定理．连接O1O2，O1A，O2C．根据切线的性质定理和勾股定理求解练习1：如图2，⊙O1与⊙O2相交于A、B．已知两圆的半径r1=10，r2=17，圆心距O1O2=21，公共弦AB等于（）A．2 B．16 C．6 D．17分析：本题综合考查了圆与圆、相交两圆的性质．注意：相交两圆的连心线，垂直平分公共弦．连接O 1A ，O 2A ，由相交两圆的连心线，垂直平分公共弦可得AB ⊥O 1O 2，且AD=BD ，设AD=x ，O 2D=y ，O 1D=21-y ，根据勾股定理列方程组，求解即可前面两道题是题目体现两圆相交 辅助线的做法求切线和公共弦的问题，下面我们来看求圆心距和相关角的度数。

练习2：已知相交两圆的半径分别为5cm 和4cm ，公共弦长为6cm ，则这两个圆的圆心距是 cm ．分析：此题综合运用了相交两圆的性质以及勾股定理．注意此题应考虑两种情况．注意此题应考虑两种情况（图3和图4）．练习3如图5，⊙O 1和⊙O 2相交于点A ，B ，它们的半径分别为2和 ，公共弦AB 长为2，若圆心O 1、O 2在AB 的同侧，则∠O 1A O 2= 度．分析：主要考查了相交圆中的相关性质：连心线垂直平分公共弦。

利用特殊直角三角形的性质求角的度数或利用三角函数值求角的度数．有以上例题及练习可得出两圆相交 求切线长，公共弦，连心线的长度及相关角的度数问题，可尝试运用歌诀。

图2A B 关于圆中常用的几种辅助线有关圆的中考，题目变化灵活，在历年各地中考题中均占有较大比例。

在解答与圆有关的题目时，常常需要作辅助线，以便在已知和结论之间“牵线搭桥”，从而使分散条件集中化，隐含条件明显化，难点分散简易化，达到解决问题的目的。

1、有弦时，可从圆心作与弦垂直的线段；或连结半径。

例1：(2006·广东)如图1，AB 是⊙O 的弦，半径OC 、OD 分别交AB 于点E 、F ，且AE=BF ，请你找出线段OE 与OF 的数量关系，并给予证明。

解析：解法1，有弦，可从圆心作与弦垂直的线段，用垂径定理。

OE=OF 。

过点O 作OM ⊥AB 于点M ，则AM=BM ，又AE=BF ，故EM=FM ，从而OM 垂直平分EF ，所以OE=OF 。

解法2，此题也可利用全等来证明。

连结半径OA 、OB ，则OA=OB ，故∠A=∠B ，又AE=BF ，所以△AOE ≌△BOF(SAS)，由此OE=OF ； 本题源于课本，巧妙地加以变化，成了一道开放性试题，学生解题时因为有基础铺垫，既增加了自信，又可以提高数学素养。

2、遇到直径时，可作直径所对的圆周角。

例2：(2006·烟台)如图2，从⊙O 外一点A 作⊙O 的切线AB 、AC ，切点分别为B 、C ，且⊙O 直径BD=6，连结CD 、AO 。

⑴求证：CD ∥AO ； ⑵设CD=ｘ，AO=ｙ，求ｙ与ｘ之间的函数关系式，并写出自变量ｘ的取值范围。

解析：有直径，可作直径所对的圆周角得直角。

⑴连结BC 交AO 于点E 。

∵AB 、AC 是⊙O 的切线，∴AB=AC ，∠CAO=∠BAO ，∴AO ⊥BC ，∴∠BEO=90°，∵BD 是⊙O 的直径，∴∠BCD=90°，∴∠BCD=∠BEO ，∴CD ∥AO ；⑵∵CD ∥AO ，∴∠D=∠AOB ，∵AB 是⊙O 的切线，BD 是直径，∴∠BCD=∠ABO=90°∴△BCD ∽△ABO ，∴BD ∶AO=CD ∶BO ，∴6∶y=x ∶3，∴y=x18，0＜x ＜6。

圆中的重要模型之辅助线模型(八大类)在平面几何中，与圆有关的许多题目需要添加辅助线来解决。

百思不得其解的题目，添上合适的辅助线，问题就会迎刃而解，思路畅通，从而有效地培养学生的创造性思维。

添加辅助线的方法有很多，本专题通过分析探索归纳八类圆中常见的辅助线的作法。

模型1、遇弦连半径(构造等腰三角形)【模型解读】已知AB 是⊙O 的一条弦，连接OA ，OB ，则∠A =∠B ．在圆的相关题目中，不要忽略隐含的已知条件。

当我们要解决有关角度、长度问题时，通常可以连接半径构造等腰三角形，利用等腰三角形的性质、勾股定理及圆中的相关定理，还可连接圆周上一点和弦的两个端点，根据圆周角的性质可得相等的圆周角，解决角度或长度的计算问题1(2022·山东聊城·统考中考真题)如图，AB ，CD 是⊙O 的弦，延长AB ，CD 相交于点P ．已知∠P =30°，∠AOC =80°，则BD 的度数是()A.30°B.25°C.20°D.10°【答案】C【分析】如图，连接OB ，OD ，AC ，先求解∠OAC +∠OCA =100°，再求解∠PAO +∠PCO =50°，从而可得∠BOA +∠COD =260°，再利用周角的含义可得∠BOD =360°-80°-260°=20°，从而可得答案．【详解】解：如图，连接OB ，OD ，AC ，∵∠AOC =80°，∴∠OAC +∠OCA =100°，∵∠P =30°，∴∠PAO +∠PCO =50°，∵OA =OB ，OC =OD ，∴∠OBA =∠OAB ，∠OCD =∠ODC ，∴∠OBA +∠ODC =50°，∴∠BOA +∠COD =260°，∴∠BOD =360°-80°-260°=20°．∴BD的度数20°．故选：C ．【点睛】本题考查的是圆心角与弧的度数的关系，等腰三角形的性质，三角形的内角和定理的应用，掌握“圆心角与弧的度数的关系”是解本题的关键．2(2023•南召县中考模拟)如图，⊙O 的直径AB 与弦CD 的延长线交于点E ，若DE =OB ，∠AOC =84°，则∠E 等于()A.42°B.28°C.21°D.20°【分析】利用OB =DE ，OB =OD 得到DO =DE ，则∠E =∠DOE ，根据三角形外角性质得∠1=∠DOE+∠E ，所以∠1=2∠E ，同理得到∠AOC =∠C +∠E =3∠E ，然后利用∠E =13∠AOC 进行计算即可．【解答】解：连结OD ，如图，∵OB =DE ，OB =OD ，∴DO =DE ，∴∠E =∠DOE ，∵∠1=∠DOE +∠E ，∴∠1=2∠E ，而OC =OD ，∴∠C =∠1，∴∠C =2∠E ，∴∠AOC =∠C +∠E =3∠E ，∴∠E =13∠AOC =13×84°=28°．故选：B ．【点评】本题考查了圆的认识：掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等)．也考查了等腰三角形的性质．3(2023·江苏沭阳初三月考)如图，已知点C 是⊙O 的直径AB 上的一点，过点C 作弦DE ，使CD =CO ．若AD 的度数为35°，则BE 的度数是．【答案】105°．【分析】连接OD 、OE ，根据圆心角、弧、弦的关系定理求出∠AOD =35°，根据等腰三角形的性质和三角形内角和定理计算即可．【解析】解：连接OD 、OE ，∵AD的度数为35°，∴∠AOD =35°，∵CD =CO ，∴∠ODC =∠AOD =35°，∵OD =OE ，∴∠ODC =∠E =35°，∴∠DOE =180°-∠ODC -∠E =180°-35°-35°=110°，∴∠AOE =∠DOE -∠AOD =110°-35°=75°，∴∠BOE =180°-∠AOE =180°-75°=105°，∴BE 的度数是105°．故答案为105°．【点睛】本题考查了圆心角、弧、弦的关系定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．4(2023年山东省淄博市中考数学真题)如图，△ABC是⊙O的内接三角形，AB=AC，∠BAC=120°，D 是BC边上一点，连接AD并延长交⊙O于点E．若AD=2，DE=3，则⊙O的半径为()A.10B.3210 C.210 D.310【答案】A【分析】连接OA,OC,CE, 根据等腰三角形的性质得到∠B=∠ACB=30°, 根据等边三角形的性质得到AC=OA，根据相似三角形的判定和性质即可得到结论.【详解】连接OA,OC,CE,∵AB=AC,∠BAC=120°,∴∠B=∠ACB=30°∴∠AOC=60°,∵OA=OC,∴△AOC是等边三角形,∴AC=OA,∵∠AEC=∠ACB=30°，∠CAD=∠EAC,∴△ACD∽△AEC,∴ACAD =AEAC，∴AC2=AD·AE,∵AD=2,DE=3,∴AC=AD×AE=2×2+3=10，∴OA=AC=10，即⊙O的半径为10，故选:A.【点睛】本题考查了圆周角定理，等腰三角形的性质，等边三角形的判定和性质，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质度量是解题的关键.模型2、遇弦作弦心距(解决有关弦长的问题)【模型解读】已知AB是⊙O的一条弦，过点OE⊥AB，则AE=BE，OE2+AE2=OA2。

圆的辅助线的常见添法圆的辅助线是在解决圆相关问题时常用的一种方法，通过引入辅助线，可以使问题更加清晰明了，便于解题。

本文将介绍几种常见的圆的辅助线添法。

一、直径直径是连接圆上任意两点并通过圆心的线段。

在解决问题时，可以通过引入直径来辅助解题。

例如，可以通过引入直径将圆分成两个半圆，使得问题的解法更加简单。

二、半径半径是从圆心到圆上任意一点的线段。

在解决问题时，可以通过引入半径来辅助解题。

例如，可以通过引入半径将圆分成多个扇形，从而得到问题的解答。

三、切线切线是与圆有且仅有一个交点的直线。

在解决问题时，可以通过引入切线来辅助解题。

例如，可以通过引入切线将圆分割成两个部分，从而得到问题的解答。

四、割线割线是与圆有两个交点的直线。

在解决问题时，可以通过引入割线来辅助解题。

例如，可以通过引入割线将圆分成多个部分，从而得到问题的解答。

五、弦弦是圆上任意两点之间的线段。

在解决问题时，可以通过引入弦来辅助解题。

例如，可以通过引入弦将圆分成多个扇形或三角形，从而得到问题的解答。

六、垂直线垂直线是与圆的切线垂直的直线。

在解决问题时，可以通过引入垂直线来辅助解题。

例如，可以通过引入垂直线将圆分割成更简单的形状，从而得到问题的解答。

七、弧弧是圆上两点之间的一段曲线。

在解决问题时，可以通过引入弧来辅助解题。

例如，可以通过引入弧将圆分成多个扇形，从而得到问题的解答。

八、切割切割是将圆分割成多个部分。

在解决问题时，可以通过引入切割来辅助解题。

例如，可以通过引入切割将圆分成若干个小部分，从而得到问题的解答。

九、平行线平行线是与圆的切线平行的直线。

在解决问题时，可以通过引入平行线来辅助解题。

例如，可以通过引入平行线将圆切割成更简单的形状，从而得到问题的解答。

总结：圆的辅助线是解决圆相关问题时常用的方法之一。

通过引入直径、半径、切线、割线、弦、垂直线、弧、切割和平行线等辅助线，可以使问题更加清晰明了，便于解题。

在解题过程中，可以根据具体情况选择合适的辅助线，并运用几何性质和数学方法解决问题。

圆中常用辅助线的作法圆中作辅助线的常用方法所涉关键词：（1）作弦心距，以便利用弦心距与弧、弦之间的关系与垂径定理和勾股定理解决问题。

（2）若题目中有“弦的中点”和“弧的中点”条件时，一般连接中点和圆心，利用垂径定理的推论得出结果。

（3）若题目中有“直径”这一条件，可适当选取圆周上的点，连结此点与直径端点得到90度的角或直角三角形。

（4）连结同弧或等弧的圆周角、圆心角，以得到等角。

（5）若题中有与半径（或直径）垂直的线段。

（6）若题目中有“切线”条件时，一般是：对切线引过切点的半径，(7)遇到90度的圆周角时常常连结两条弦没有公共点的另一端点。

（8）有些问题可以先证明四点共圆，借助于辅助圆中角之间的等量关系去证明。

（9）对于圆的内接正多边形的问题，往往添作边心距，抓住一个直角三角形去解决。

(10)有半圆，可作整圆由平分弦的直径必平分弦所对的弧想到补全(11) 有弦中点时，常构造三角形中位线或做弦心距.(12)圆上有四点时，常构造圆内接四边形.(13) 遇到两相交切线时（切线长）常常连结切点和圆心、连结圆心和圆外的一点、连结两切点。

作用：据切线长及其它性质，可得到：①角、线段的等量关系；②垂直关系；③全等、相似三角形。

(14)．遇到三角形的内切圆时连结内心到各三角形顶点，或过内心作三角形各边的垂线段。

作用：利用内心的性质，可得：①内心到三角形三个顶点的连线是三角形的角平分线；②内心到三角形三条边的距离相等。

(15)．遇到三角形的外接圆时，连结外心和各顶点作用：外心到三角形各顶点的距离相等。

记忆宝典辅助线，莫乱添，规律方法记心间；弦和弦心距，亲密紧相连；切点与圆心连线要领先；直角相对或共弦，应当想想辅助圆；要证直线是切线，还看是否有共点；直线和圆有共点，连出半径辅助线；直线和圆无共点，得过圆心作垂线；若遇直径想直角，灵活运用才方便。

初中数学《圆》常用辅助线构造技巧圆是初中数学中的重要内容，常常会涉及到圆的基本性质、切线、切点、弦、弦长、弧、弧长等概念。

为了更好地解题，我们可以使用一些常用的辅助线构造技巧。

下面，我将介绍几种常用的辅助线构造技巧。

1.直径是圆的特殊弦，通过任意两点连接圆心，可以得到直径。

在解题中，如果涉及到圆心和两点的位置关系，可以考虑构造直径。

2.过圆心的直线与圆的切线垂直。

当我们需要求解两个垂直的线段或角度时，可以考虑构造一条过圆心的直径，使其与需要垂直的线段或角度相交。

3.过圆心的直线将弧等分为两个等长的弧。

当我们需要将一个弧等分为两个等长的弧时，可以考虑构造一条过圆心的直线，将这个弧分割为两个等长的弧。

1.过切点的切线与圆的半径垂直。

当我们需要求解两个垂直的线段或角度时，可以考虑构造一条过切点的切线，并将其延伸至圆心，使其与需要垂直的线段或角度相交。

2.过切点的切线等于切点至圆心的半径。

当我们需要求解两个等长的线段或角度时，可以考虑构造一条过切点的切线，并将其延伸至圆心，使其与另一条需要等长的线段或角度相交。

1.弦的中点与圆心以及两个端点可以构成一个等腰三角形。

当我们需要求解与等腰三角形相关的线段或角度时，可以考虑构造一条连接弦的中点与圆心以及两个端点的直线。

2.以弦的中点为顶点的直角三角形。

当我们需要求解与直角三角形相关的线段或角度时，可以考虑构造一条连接弦的中点与两个端点的直线，并通过调整弦的位置，使其与这条直线构成一个直角。

1.弦的垂直平分线同时也是弦的中垂线。

在解题中，如果需要求解弦的垂直平分线或者弦的中垂线，可以考虑构造一条连接弦的两个端点的直线，并将其垂直平分或中垂。

2.连接弦的两个端点与圆心的线段是一个等角二段线。

当我们需要求解与等角二段线相关的线段或角度时，可以考虑构造一条连接弦的两个端点与圆心的直线。

以上是一些常用的圆的辅助线构造技巧，通过合理地运用这些技巧，可以帮助我们更好地理解和解题。

《圆》常用辅助线构造技巧圆是数学中非常重要的一个几何形状，对于圆的构造和分析，辅助线构造技巧是不可或缺的工具之一、辅助线的引入可以帮助我们简化问题、找到关键信息、发现隐藏的特性和关系，从而更好地解决问题。

在本文中，我将介绍一些常用的辅助线构造技巧，希望能对大家的圆的学习有所帮助。

1.划分弧长和角度：当需要将圆上的弧划分成等长的部分时，可以引入辅助线。

例如，要将一个给定的圆上的弧ACB分成5等份。

我们可以在弧上选择两点D和E，并通过D、E和圆心O分别画两条半径，使其与弧ACB交于点F和G。

然后通过直线OF、OG将圆分成5个等弧。

2.寻找垂直角：当我们需要判断两条线段是否垂直时，可以通过引入垂直辅助线来判断。

例如，当我们需要判断线段AB和CD是否垂直时，可以通过引入半径OC和OD，然后判断角AOC和角COD是否互为垂直角来判断。

3.寻找平行线段：当我们需要判断两条线段是否平行时，可以通过引入平行辅助线来判断。

例如，当我们需要判断线段AB和CD是否平行时，可以通过引入直径AC和BD，然后判断角ABC和角CDA是否互为对应角来判断。

4.寻找相等线段和角：当我们需要证明两条线段或两个角相等时，可以通过引入相等辅助线来证明。

例如，当我们需要证明线段AB和CD相等时，可以通过引入直径AC和BD，然后通过三角形ABC和三角形CDA的相似性来证明。

5.寻找点的位置关系：当我们需要判断一个点与一条线段或一条弧的位置关系时，可以通过引入辅助线来判断。

例如，当我们需要判断点P是否在线段AB上时，可以通过引入半径OP，然后判断角AOP和角BOP是否相等来判断。

6.寻找三角形的性质：圆与三角形的关系是数学中一个重要的研究领域，通过引入辅助线可以有助于研究三角形的特性。

例如，当我们需要研究圆内接三角形的性质时，可以通过引入辅助线将圆分成若干个等弧，然后通过引入半径和垂直辅助线来研究三角形的边长和角度。

除了以上的常用辅助线构造技巧外，还有许多其他的技巧可以应用于解决圆的问题。

中考数学答题技巧：圆与圆位置关系中常见辅助线的作法中考数学答题技巧：圆与圆位置关系中常见辅助线的作法圆与圆位置关系是初中几何的一个重要内容，也是学习中的难点，本文介绍圆与圆的位置关系中常见的五种辅助线的作法。

1. 作相交两圆的公共弦利用圆内接四边形的性质或公共圆周角，沟通两圆的角的关系。

例1. 如图1，⊙O1和⊙O2相交于A、B两点，过A、B分别作直线C D、EF，且CD//EF，与两圆相交于C、D、E、F。

求证：CE=DF。

图1分析：CE和DF分别是⊙O1和⊙O2的两条弦，难以直截了当证明它们相等，但通过连结AB，则可得圆内接四边形ABEC和ABFD，利用圆内接四边形的性质，则易证明。

证明：连结AB因为又因此即CE//DF又CD//EF因此四边形CEFD为平行四边形即CE=DF2. 作两相交圆的连心线利用过交点的半径、公共弦、圆心距构造直角三角形，解决有关的运算问题。

例2. ⊙O1和⊙O2相交于A、B两点，两圆的半径分别为和，公共弦长为12。

求的度数。

图2分析：公共弦AB可位于圆心O1、O2同侧或异侧，要求的度数，可利用角的和或差来求解。

解：当AB位于O1、O2异侧时，如图2。

连结O1、O2，交AB于C，则。

分别在和中，利用锐角三角函数可求得故当AB位于O1、O2同侧时，如图3图3则综上可知或3. 两圆相切，作过切点的公切线利用弦切角定理沟通两圆中角的关系例3. 如图4，⊙O1和⊙O2外切于点P，A是⊙O1上的一点，直线A C切⊙O2于C，交⊙O1于B，直线AP交⊙O2于D。

求证PC平分。

图4分析：要证PC平分，即证而的边分布在两个圆中，难以直截了当证明。

若过P作两圆的公切线PT，与AC交于T易知由弦切角定理，得又是的一个外角因此又从而有即PC平分4. 两圆相切，作连心线利用连心线通过切点的性质，解决有关运算问题。

例4. 如图5，⊙O1与半径为4的⊙O2内切于点A，⊙O1通过圆心O 2，作⊙O2的直径BC，交⊙O1于点D，EF为过点A的公切线，若，求的度数。

CM O N 圆中常作哪些辅助线?通过作辅助线能使复杂问题简单化，圆问题中常用的辅助线是哪些呢？现把一些规律总结如下：弦与弦心距，密切紧相连. 直径对直角，圆心作半径. 已知有两圆，常画连心线. 遇到相交圆，连接公共弦. 遇到相切圆，作条公切线. “有点连圆心，无点作垂线.” 切线证明法，规律记心间.一、作弦心距.在解决有关弦的问题时，常常作弦心距，以利用垂经定理或圆心角、弦、弦心距之间的关系定理及推论.因此“弦与弦心距，密切紧相连.”.例 1.如图，ＡＢ是⊙O 的直径,PO⊥AB 交⊙O 于 P 点，弦 PN 与 AB 相交于点 M，求P证：PM•PN=2PO2.1分析：要证明PM•P N=2PO²，即证明PM•PN =POA B2²，1过 O 点作 OC⊥PN 于 C，根据垂经定理PN =PC，只需证明2。

⨯。

∆PMOPM•PC=PO²，由PO = P M，“三点定型”法可判断需证明 Rt△POC∽Rt△PMO.。

⨯ ∆POCPC PO1证明: 过圆心 O 作 OC⊥PN 于 C，∴PC= PN2∵PO⊥AB, OC⊥PN，∴∠MOP=∠OCP=900.又∵∠OPC=∠MPO，∴Rt△POC∽Rt△PMO.∴ PO = PC PM，即∴PO2= PM•PC. PO1∴PO2= PM•PN，∴PM•PN=2PO2.2二、连结半径圆的半径是圆的重要元素，圆中的许多性质如：“同圆的半径相等”和“过切点的半径与切线相互垂直”都与圆的半径有关.连结半径是常用的方法之一.例 2．已知：△ABC 中，∠B=900，O 是 AB 上一点，以 O 为圆心，以 OB 为半径的圆切 AC 与 D 点，交 AB 与 E 点，AD=2，AE=1.求证:CD 的长. CD 分析：D 为切点，连结 DO，∠ODA=900.根据切线长定理AE O BCD=CB.DO=EO= 半径r，在Rt△ADO 中根据勾股定理或Rt△ADO~ Rt△ABC，求出CD.证明: 连结DO∴OD⊥AC 于 D, ∴∠OCP=900.∵AB 过 O 点, ∠B=900.∴BC 为⊙O 的切线, ∴CD=CB设 CD=CB=x,DO=EO=y在Rt△ADO 中，AO2 =AD2+ DO2，AD=2，AE=13∴(1+y)2=22+y2, ∴ y=23 3在Rt△ABC 中，AC2 =AB2+ BC2，即(2+x)2=(1+ + )2+x2, ∴x=32 2∴CD=3.三、连结公共弦D 在处理有关两圆相交的问题时，公共弦像一把AEBPAE“钥匙”，常常可以打开相应的“锁”，因此“遇到相交圆，连接公共弦.”。

圆中常见辅助线的添加口诀及技巧半径与弦长计算,弦心距来中间站;圆上若有一切线,切点圆心半径连;要想证明是切线,半径垂线仔细辨;是直径,成半圆,想成直角径连弦;弧有中点圆心连,垂径定理要记全;圆周角边两条弦,直径和弦端点连;要想作个外接圆,各边作出中垂线;还要作个内切圆,内角平分线梦园;如果遇到相交圆,不要忘作公共弦;若是添上连心线,切点肯定在上面;二：圆中常见辅助线的添加：1、遇到弦时解决有关弦的问题时1、常常添加弦心距,或者作垂直于弦的半径或直径或再连结过弦的端点的半径;作用：①利用垂径定理；②利用圆心角及其所对的弧、弦和弦心距之间的关系；③利用弦的一半、弦心距和半径组成直角三角形,根据勾股定理求有关量;2、常常连结圆心和弦的两个端点,构成等腰三角形,还可连结圆周上一点和弦的两个端点;作用：①可得等腰三角形；②据圆周角的性质可得相等的圆周角;2、遇到有直径时常常添加画直径所对的圆周角;作用：利用圆周角的性质,得到直角或直角三角形3、遇到90°的圆周角时常常连结两条弦没有公共点的另一端点;作用：利用圆周角的性质,可得到直径;4、遇到有切线时1常常添加过切点的半径见切点连半径得垂直作用：利用切线的性质定理可得OA⊥AB,得到直角或直角三角形;5、遇到证明某一直线是圆的切线时1若直线和圆的公共点还未确定,则常过圆心作直线的垂线段,再证垂足到圆心的距离等于半径;2若直线过圆上的某一点,则连结这点和圆心即作半径,再证其与直线垂直;6、遇到三角形的内切圆时连结内心到各三角形顶点,或过内心作三角形各边的垂线段;作用：利用内心的性质,可得：1内心到三角形三个顶点的连线是三角形的角平分线； 2内心到三角形三条边的距离相等7、遇到三角形的外接圆时,连结外心和各顶点作用：外心到三角形各顶点的距离相等;例题1、如图,已知△ABC内接于⊙O,∠A=45°,BC=2,求⊙O的面积; 例题2、如图,弦AB的长等于⊙O的半径,点C在弧AMB上,则∠C的度数是________.例题3、如图,AB是⊙O的直径,AB=4,弦BC=2,∠B=例题4、如图,AB、AC是⊙O的的两条弦,∠BAC=90°,AB=6,AC=8,⊙O的半径是例题5、如图所示,已知AB是⊙O的直径,AC⊥L于C,BD⊥L于D,且AC+BD=AB;求证：直线L与⊙O相切;例题6、如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B,C是弧AB 上任意一点,过C作⊙O的切线分别交PA、PB于D、E,若△PDE的周长为12,则PA长为______________例题7、如图,△ABC中,∠A=45°,I是内心,则∠BIC=例题8、如图,Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB 于D,E,F,求Rt△ABC的内心I与外心O之间的距离．课后练习1、已知：P是⊙O外一点,PB,PD分别交⊙O于A、B和C、D且AB=CD.求证：PO平分∠BPD．2、如图,ΔABC中,∠C=90°,圆O分别与AC、BC相切于M、N,点O在AB上,如果AO=15㎝,BO=10㎝,求圆O的半径.3、已知：□ABCD的对角线AC、BD交于O点,BC切⊙O于E点.求证：AD也和⊙O相切.4、如图,学校A附近有一公路MN,一拖拉机从P点出发向PN方向行驶,已知∠NPA=30°,AP=160米,假使拖拉机行使时,A周围100米以内受到噪音影响,问：当拖拉机向PN方向行驶时,学校是否会受到噪音影响请说明理由.如果拖拉机速度为18千米∕小时,则受噪音影响的时间是多少秒总结:弦心距、半径、直径是圆中常见的辅助线;圆中辅助线添加的常用方法圆是初中几何中比较重要的内容之一,与圆有关的问题,汇集了初中几何的各种图形概念和性质,其知识面广,综合性强,随着新课程的实施,园的考察主要以填空题,选择题的形式出现,不会有比较繁杂的证明题,取而代之的是简单的计算;圆中常见的辅助线有：1作半径,利用同圆或等圆的半径相等； 2涉及弦的问题时,常作垂直于弦的直径弦心距,利用垂径定理进行计算和推理； 3作半径和弦心距,构造直角三角形利用勾股定理进行计算； 4 作直径构造直径所对的圆周角； 5 构造同弧或等弧所对的圆周角； 6遇到三角形的外心时,常连接外心与三角形的各个顶点； 7 已知圆的切线时,常连接圆心和切点半径； 8 证明直线和园相切时,有两种情况：1已知直线与圆有公共点时,连接圆心与公共点,证此半径与已知直线垂直 ,简称“有点连线证垂直,”2已知直线与圆无公共点时,过圆心作已知直线的垂线段,证它与半径相等,简称“无点做线证相等”此外,两解问题是圆中经常出现的问题,涉及弧,弦,与圆有关的角,点与圆,直线与圆,圆与圆的位置关系等知识,着重考察思维的完备性和严谨性,应特别引起重视。