当前位置：文档之家 › 11.5 两个三角形全等的条件第一课时

11.5 两个三角形全等的条件第一课时

  • 格式：doc
  • 大小：83.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

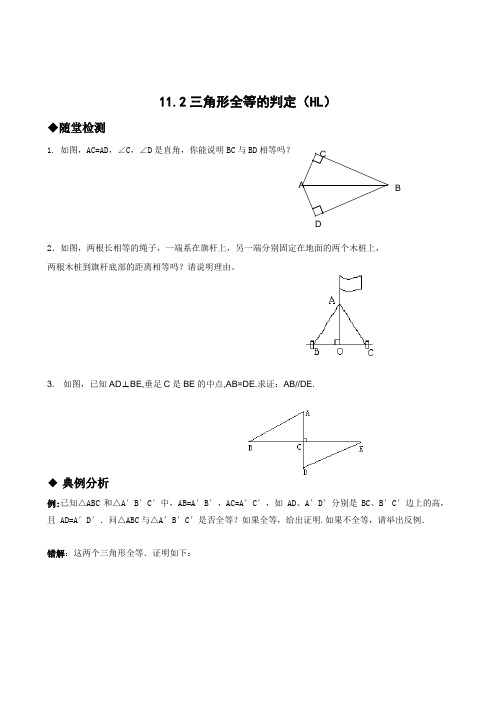
11.5三角形全等的判定(HL)

11.5三角形全等的判定(HL)

11.2三角形全等的判定（HL ）◆随堂检测1. 如图，AC=AD ，∠C ，∠D 是直角，你能说明BC 与BD 相等吗？2．如图，两根长相等的绳子，一端系在旗杆上，另一端分别固定在地面的两个木桩上， 两根木桩到旗杆底部的距离相等吗？请说明理由。

3. 如图，已知AD ⊥BE,垂足C 是BE 的中点,AB=DE.求证：AB//DE.◆ 典例分析例:已知△ABC 和△A ′B ′C ′中，AB=A ′B ′，AC=A ′C ′，如 AD 、A ′D ′分别是BC 、B ′C ′边上的高，且 AD=A ′D ′．问△ABC 与△A ′B ′C ′是否全等？如果全等，给出证明.如果不全等，请举出反例．错解：这两个三角形全等．证明如下：D B如图1，在Rt△ABD和 Rt△A′B′D′中，∵AB=A′B′，AD=A′D′∴Rt△ABD≌Rt△A′B′D′.∴BD=B′D′同理可证 DC=D′C′，∴BC=B′C′在△ABC和△A′B′C′中，∵AB=A′B′，AC=A′C′，BC=B′C′，∴△ABC≌△A′B′C′.评析：这两个三角形不一定全等．当这两个三角形均为钝角(或锐角)三角形时全等；若一个是锐角三角形，一个是钝角三角形时就不可能全等．如图2，虽有AB=A′B′，AC=A′C′，但BC≠B′C′，因此这两个三角形不全等．◆课下作业●拓展提高4.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.(1) _______,∠A=∠D ( ASA )(2) AC=DF,________ (SAS)(3) AB=DE,BC=EF ( )(4) AC=DF, ______ ( HL )(5) ∠A=∠D, BC=EF ( )(6) ________,AC=DF ( AAS )5.小明既无圆规，又无量角器，只有一个三角板，他是怎样画角平分线的呢？他的具体做法如下：在已知∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA、OB的垂线交点为P,画射线OP.则OP平分∠AOB。

《三角形全等的判定(第1课时)》PPT优质课件

《三角形全等的判定(第1课时)》PPT优质课件

使△ABF≌△ECD ，还需要条件 BF=CD___ (填一个
条件即可）.
A
E
B
D
F
C
课堂检测
2.如图，AB＝CD，AD＝BC, 则下列结论：
①△ABC≌△CDB； ②△ABC≌△CDA；
③△ABD ≌△CDB； ④ BA∥DC.
正确的个数是 ( C )
A
D
A . 1个 C. 3个
B. 2个 D. 4个 B
课堂检测
2. 已知：∠AOB．求作：∠A'O'B'，使∠A'O′B'=∠AOB,
（1）如图1，以点O为圆心，任意长为半径画弧，分别交OA，
OB于点C,D；
（2）如图2，画一条射线O′A′，以点O′为圆心，OC长为半径 作弧，交O′A′于点C′； （3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧 交于点D′；
所画的弧交于点D′；
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB．
依据是什 么？
链接中考 1.如图，EF=BC，DF=AC，DA=EB．求证∠F=∠C．
证明：∵DA=BE，∴DE=AB， 在△ABC和△DEF中， AB=DE
AC=DF BC=EF，
∴△ABC≌△DEF（SSS），∴∠C=∠F．
3.已知△ABC ≌△DEF，找出其中相等的边与角.
A
D
B
①AB=DE
④ ∠A= ∠D
C
E
② BC=EF
⑤ ∠B=∠E
F
③ CA=FD
⑥ ∠C= ∠F
即：三条边分别相等，三个角分别相等的两个三角形全等．
探究新知 【思考】如果只满足这些条件中的一部分,那么能保证 △ABC≌△DEF 吗?

《两个三角形全等的条件》课件1(13页)(冀教版七年级下)

《两个三角形全等的条件》课件1(13页)(冀教版七年级下)
河北教育出版社 七年级下册
两个三角形
对应边和对应 角相等情况
A
A`
B
C
C`
A
A`

B
C
∠B=∠B BC=BC
是否全等 不全等 不全等
两个三角形
A
A`
B
C
A
A`
B
C
A
AC∥A`C`
A`
B
C`
C
对应边和对应 角相等情况
是否全等
AB=A`B BC=BC
不全等
∠B=∠B BC=BC
不全等
∠B=∠B ∠ACB=∠A`C`B
B
C B′
C′
边边边 如果两个三角形的三边对应相 等，那么这两个三角形全等 （SSS）
用线连接下列图形中的全等三角形
8
6 Ⅰ
9
8 Ⅱ7
5
8
8Ⅲ
5
5
8
Ⅴ 7
5
8Ⅵ
8
8 Ⅶ6
9
已知：如图，AB=AC,AD=AE,BD=CE. 试找出图中的全等三角形，并说明理由
A
△ABD≌△ACE
BD
△ABE≌△ACD
EC
三角形的稳定性：只要三角形的三边确定，它的形状
和大小就完全确定了这一特殊性质叫做三角形的稳定性
谈一谈你今天的收获和体会
（1）两个三角形全等的条件：SSS. （2）三角形的稳定性
已知:△ABC≌△A′B′C′,AB=11cm,
AC=6cm. △ A ′B′C′周长为 29cm,
A′C′=6cm.
求:BC=? A′B′=? B′C′=?
A
A′
不全等
实验：

三角形全等的判定(第一课时)

三角形全等的判定(第一课时)

数$。
SSS判定定理的证明
第十步
根据三角形的性质，我们知道三角形的一个外角等于与它 不相邻的两个内角之和，即$angle A+angle B=angle C$。
第十一步
根据三角形的性质，我们知道三角形的一个内角等于与它 相邻的两个外角之差的一半，即$angle A=frac{1}{2}(angle B+angle C)$。
第三步，由全等三角形的性质，我们知道$BC = AC$。
ASA判定定理和AAS判定定理的应用
应用一
当已知两个三角形有两个角和一 个角的对边分别相等时，我们可 以使用ASA或AAS判定定理来判 断这两个三角形是否全等。
应用二
当已知两个三角形有一个角、一 边和另一角的对边分别相等时， 我们可以使用ASA或AAS判定定 理来判断这两个三角形是否全等 。
三角形全等的判定(第一课时)
目录 Contents
• 三角形全等的基本概念 • 三角形全等的SSS判定 • 三角形全等的SAS判定 • 三角形全等的ASA判定和AAS判定 • 三角形全等的特殊情况
01
三角形全等的基本概念
三角形全等的定义
01
三角形全等是指两个三角形能够 完全重合，即它们的形状和大小 都相同。
实例二
在平面几何中，我们经常需要证明两个三角形是全等的。利用SAS判定定理，我们可以很容易地证明两个三角形 是全等的。例如，已知三角形ABC和三角形DEF，其中AB=DE，BC=EF，并且角A=角D，角B=角E。根据SAS判 定定理，我们可以证明三角形ABC和三角形DEF是全等的。
04
三角形全等的ASA判定和 AAS判定
ASA判定定理和AAS判定定理的证明
第三步，由全等三角形的性质，我们知道$BC = AC$。 AAS判定定理证明

11.5 两个三角形全等的条件第一课时

11.5 两个三角形全等的条件第一课时
1
体会三角形全 等的判断方法。 认识一个条 件、两个条件、三 个角对应相等，都 不能判断两个三角 形全等。 提出问题，调
等可以判断两个三角形全等吗？
动学习积极性。
请同学们分小组活动： 1）用一根长 13 cm 的细铁丝，折成一个边长分别是 3 cm , 4 cm , 6 cm 的三角形．把你做的三角形和同学做的三角形进 行比较，它们能重合吗？ 2）用同一根细铁丝，余下 1 cm ，用其余部分折成一个边长 分别是 3cm , 4 cm , 5 cm 的三角形，再和同学做的三角形 进行比较，它们能重合吗？ 3）不同小组用同一根细铁丝，任取一组能构成三角形的三边长 的数据，和同桌同学分别按这些数据折三角形，折成的两个三 角形能重合吗？ 通过试验，可以得出什么结论呢？ 文字为 数学符号表示为：因为 所以
设计意图 师生随笔
认识学习判定 方法的意义。
B
C
同学们会说这需要量一下这个三角形的边长和内角的度 数，那么请问：你准备量哪几条边长，哪几个内角的度数？能 尽量少吗？ 二、 动手 操作， 合 作发现 活动 1 请大家通过填写课本 P144 的表格来思考这个问题． 1．一个条件（边或角）可以判断两个三角形全等吗？ 2．两个条件（两边、两角或一边一角）可以判断两个三角形全 等吗？ 3．三个角对应相等可以判断两个三角形全等吗？ 活动 2 探究 SSS 三个角对应相等不能判断两个三角形全等，那么三条边对应相
A D
学生动手操 作，小组交流。经 历几种不同情形的 操作和探究过程， 让学生发现和体会 “两个三角形的三 边对应相等，这两 个三角形全等。 ”
。 ， 。
通过实验总结 “SSS” 。
B
C
E
活动 3．三角形的稳定性 教师归纳：在刚才的实验中，我们还认识到一个事实： 只要三角形的三条边的长度确定了，三角形的形状和大小也就 唯一确定了，三角形所具有的这一特殊性质叫做三角形的稳定 性。 1、老师这里有一个镜框，它是四边形的，我想把这幅漂亮的风 景画装上去，可是镜框很不牢固，你有什么好办法，帮老师把 它固定的？ 2、 请各组代表上讲台展示， 拉一拉。 (体会四边形的不稳定性) 3、 你们把支架和镜框订成了什么图形？说明三角形具有什么？ （稳定性） 4、你发现生活中哪些地方利用了三角形的稳定性？ 三、 巩固 新知， 反 馈练习 例 1、下列哪些三角形全等

11.5两个三角形全等的条件

11.5两个三角形全等的条件
30° 30° 30°
三角 形全 等的 探究
②两内角： 两内角：
30° 50° 30° 50° 可以发现给出 两个条件时画出的 三角形也不能保证 一定全等。 一定全等。
2cm 4cm 2cm 4cm
③两边： 两边：
3.给出三个条件： 3.给出三个条件： 给出三个条件 ①三个内角： 三个内角：
30° 50° 50° 30°
夹角写在中间 D
2
C
已知：AB=AC，AD=AE， 已知：AB=AC，AD=AE，∠ 1= ∠2 求证： ABD≌△ 求证：△ABD≌△ACE
B
1 3 2
A
C
D
E
证明：∵∠1=∠2 已知） 证明：∵∠1=∠2（已知） ∴∠1+∠3=∠2+∠3 ∴∠1+∠3=∠2+∠3 B 即∠BAD ＝∠CAE ABD和 ACE中 在△ABD和△ACE中， AB=AC（已知） AB=AC（已知） ∠BAD=∠CAE（已证） ∠BAD=∠CAE（已证） C AD=AE（已知） AD=AE（已知） ∴△ABD≌△ACE ABD≌△
用符号语言表达为： 用符号语言表达为：
在△ABC和△DEF中 ABC和 DEF中 已知） AC=DF （已知） ∠C=∠F（已知） C=∠F（已知） 已知） BC=EF （已知） △ABC≌△DEF中（SAS） ABC≌△DEF中 SAS）
B
A
D
C F E
夹角写在中间
自学书146页后填空： 自学书146页后填空： 146页后填空 三角形具有 稳定性 .四边形不具有稳定性. A 147页练习 页练习2 书147页练习2题答案 D B C 连接AC AC就可以把四边形分成两个全等三角形 连接AC就可以把四边形分成两个全等三角形 ACB和 CAD中 在△ACB和△CAD中 AB=CD(已知 已知) AB=CD(已知) AC=CA（公共边） AC=CA（公共边） 注意公共边的写法 AD=CB(已知 已知) AD=CB(已知) ACB≌△CAD(SSS)(抄书上) D(SSS)(抄书上 ∴△ACB≌△CAD(SSS)(抄书上)

七年级数学下册：11.5 两个三角形全等的条件(教案)冀教版

两个三角形全等的条件（第1课时）
教学任务分析
教学流程安排
课前准备
教学过程设计
1．一个条件（边或角）可以判断两个三角形全等吗？
2．两个条件（两边、两角或一边一角）可以判断两个三角形全等吗？
3．三个角对应相等可以判断两个三角形全等吗？学生回答，教师点评．认识一个条件、
两个条件、三个
角对应相等，都
不能判断两个
三角形全等．
活动2 探究SSS
三个角对应相等不能判断两个三角形全等，那么三条边对应相等可以判断两个三角形全等吗？教师提出问题．提出问题，调动
学习积极性．
请同学们按课本P153“一起探究”中的步骤
做实验．
学生操作，教师巡视指导．体会SSS．
通过实验三条边对应相等的两个三角形全等吗？
如果两个三角形的三条边对应相等，那么这两个三角形全等．这个事实可以简记为“边边边”或“SSS”师生共同总结“SSS”．通过实验总结
“SSS”．
在刚才的实验中，我们还认识到一个事实：只要三角形的三条边的长度确定了，三角形的形状和大小也就唯一确定了，三角形所具有的这一特殊性质叫做三角形的稳定性．教师讲述．学习三角形的
稳定性．
在工程建筑和日常生活中常用到三角形的稳定性，你能举出一些例子吗？学生回答，教师点评．三角形的稳定
性的应用．
活动3 课堂练习
请做课后练习P155．
学生解答，教师巡视指导．
注意：第2题应用公共边．巩固“SSS”和三角形的稳定性．。

探索三角形全等的条件第一课时参考课件


A
C
O
B
D
自主 合作 探究 互动
画法: 1. 画线段AB=2cm.
2. 分别以A,B为圆心,3cm,4cm长为 半径 画两条圆弧,交于点C.
3. 连结CA,AB.
与同伴比一比，发现什么？
有三条边对应相等的两个三角形全等
记做“边边边”或“SSS”
做一做
有一些长度适当的木条，用钉子把它们分别 钉成三角形和四边形，并拉动它们。
三角形的大小和形状是固定不变的，而四边 形的形状会改变。
探索三角形全等的条件
1. 怎样的两个三角形是全等三角形？
完全重合的两个三角形全等
2.两个全等三角形具有怎样的性质？
A
E
B
CF
G
全等三角形的对应边相等，对应角相等
3. 两个三角形需满足几个条件才能证明它们全等？
一个条件
（1）有一条边对应相等的三角形 （2）有一个角对应相等的三角形
两个条件
（1) 三角形的一个角 ,一条边对应相等
只要三角形三边的长度确定了，这个三角形的形 状和大小就确定，三角形的这个性质叫 三角形的稳定性。
1．如何判断老师在一张纸上画的这两个三角形是否全等？
A
E
B
C
F
G
量一量 AB= 4CM
EF=4CM
BC=6CM
FG=6CM
AC= 5.4CM EG=5.4CM ∵ AB=EF，BC=FG，AC=EG
明理由。
A
D
B
C
1. 已知三边长画三角形的方法. 2. 三角形全等条件一. 3. 三角形的稳定性.
备选练习
1.如图，已知AB=AC，BD=CD，则图中对应

两个三角形全等的条件(第1课时)

注意：第2题应用公共边．
巩固“SSS”和三角形的稳定性．
活动4 回顾与反思
1．三个条件就一定能判定三角形全ห้องสมุดไป่ตู้吗？
2．三角形的稳定性指的是什么？
学生回答，教师点评．
总结判定三角形全等的方法和SSS．
布置作业
课后习题（155）第1、2、3题．
感谢您的阅读，祝您生活愉快。
只要三角形的三条边的长度确定了，三角形的形状和大小也就唯一确定了，三角形所具有的这一特殊性质叫做三角形的稳定性．
教师讲述．
学习三角形的稳定性．
在工程建筑和日常生活中常用到三角形的稳定性，你能举出一些例子吗？
学生回答，教师点评．
三角形的稳定性的应用．
活动3 课堂练习
请做课后练习P155．
学生解答，教师巡视指导．
两个三角形全等的条件（第1课时）
教学任务分析
教学
目标
知识与技能
1．知道三条边对应相等的两个三角形全等，知道三角形的稳定性；
2．会运用SSS判定两个三角形全等．
过程与方法
经历探究三角形全等条件的过程．
情感态度与
价值观
在探究三角形全等的条件的过程中，培养学生重视实践的意识；通过学习三角形稳定性的实例，培养学生运用数学的意识．
问题与情景
师生行为
设计意图
活动1 观察与思考
我们知道三条边、三个角对应相等的两个三角形能够完全重合，即两个三角形全等．
我们能否用较少的条件判断两个三角形全等呢？
教师讲述．
认识学习判定方法的意义．
请大家通过填写课本P152的表格来思考这个问题．
学生填表，教师巡视指导．
体会三角形全等的判断方法．
1．一个条件（边或角）可以判断两个三角形全等吗？

《两个三角形全等的条件》课件


A
D
以上两题综合在一
F E
起，分两步证： 创造条件，证明全 等.
C
B
11
证明：∵AD//BC(以知) ∴ ∠A= ∠B(两直线平行内错角相等) ∵AF=BE(以知) ∴AF+FE=BE+FE(等量加等量和相等)
即: AE=FB 在△ADE和△BCF中 AD=CB(以知) ∠A= ∠B(以证) AE=FB(以证)
1
教学目的：
1.使学生比较熟练地掌握三角 形全等的判定公理.
2.使学生初步掌握寻找两个三 角形全等的非已知条件的思 路和方法.
2
教学重点：
如何运用判定公理1来证明两 个三角形全等.
重点
3
教学难点：
证明题的书写格式.
难点
4
复习：
1. 叙述全等三角形判定公理1. 2. 如图：已知AB、CD相交于点O ，
则△ADE ≌ △BCF(SAS)
12
小结：
1、边角边公理： 1）关系：角是两边的夹角。 2）在找关系中，一定要注意对应
关系。
要点
13
2、 三个条件的来源：
1）来自“已知”
直接给出
2）来自图形
公共元素
3） 在图形和已知条件中挖掘。
要点
14
3. 注意证明格式： 分两步：
1）创造条件. 2）证明全等.
要点
15
AO=BO，CO=DO. 求证A：△AOC≌△BODD
O
C
B
5
新课
利用“边角边”公理证明两 个三角形全等时，必须具备三 个条件，缺一不可，对于所缺 的条件如何寻找，则是证明两 个三角形全等的关键。也是本 节课我们要研究的问题。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

七年级《数学》学教案
11.5两个三角形全等的条件（第一课时）
滦南县长宁镇初级中学贺艳霞
教学目标：
知识目标：
1．使学生掌握“边边边”公理，并会用它证明三角形全等。

2．了解三角形的稳定性。

能力目标：通过观察几何图形，培养学生的识图能力，培养学生的动手能力
情感目标：培养学生勇于创新，多方位审视问题的创造技巧。

学习重、难点:
重点：让学生经历三角形全等的条件的分析和画图验证等过程，了解两个三角形全等应有三个条件。

并能从中探索出“三边对应相等的两个三角形全等”，能应用这个条件去判定两个三角形全等和三角形的稳定性。

难点：三角形全等条件的分析与探索。

教具学具准备：
直尺，细铁丝，用木条钉成的三角框架及四边形框架。

预习导航
1．一个条件（边或角）可以判断两个三角形全等吗？
2．两个条件（两边、两角或一边一角）可以判断两个三角形全等吗？
3．三个角对应相等可以判断两个三角形全等吗？
4．三条边对应相等可以判断两个三角形全等吗？
教学过程
．若只有一条边对应相等的两个三角形全等，那这两个三角形必
．如图5，在△ABC 中，∠分别是AC 、AB 上的点，的度数。

（选做） 11.5两个三角形全等的条件
F （二） 三角形的稳定性
（一）三角形全等的条件1：SSS （三）例题2
数学符号表示为：
因为 AB=DE 解：
BC=EF
AC=DF
所以△ABC ≌△DEF
E F
B
A C。