《等腰直角三角形中地常用模型》

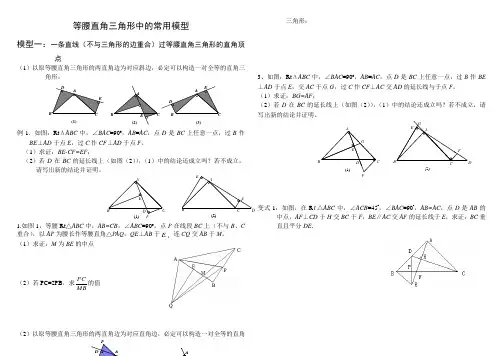
等腰直角三角形中的常用模型模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点（1）以原等腰直角三角形的两直角边为对应斜边，必定可以构造一对全等的直角三角形：例1．如图：Rt ΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥AD 于点E ，过C 作CF ⊥AD 于点F 。

（1）求证：BE-CF=EF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。

1.如图1，等腰Rt △ABC 中，AB=CB ，∠ABC =90º，点P 在线段BC 上（不与B 、C 重合），以AP 为腰长作等腰直角△P AQ ，QE ⊥AB 于E ，连CQ 交AB 于M 。

（1）求证：M 为BE 的中点（2）若PC=2PB ，求MBPC的值（2）以原等腰直角三角形的两直角边为对应直角边，必定可以构造一对全等的直角三角形：3、如图：Rt ΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥AD 于点E ，交AC 于点G ，过C 作CF ⊥AC 交AD 的延长线与于点F 。

（1）求证：BG=AF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。

变式1：如图，在R t △ABC 中，∠ACB =45º，∠BAC =90º，AB=AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE ∥AC 交AF 的延长线于E ，求证：BC 垂直且平分DE .G G B ACD E F (2)(1)FE D C B AF DAA(2)FEDC A A B C DE F (1)(2)(3)(1)DD EEC C EC A AAB变式2：等腰Rt △ABC 中，AC=AB ，∠BAC ＝90°，点D 是AC 的中点，AF ⊥BD于点E ，交BC 于点F ，连接DF ，求证：∠1=∠2。

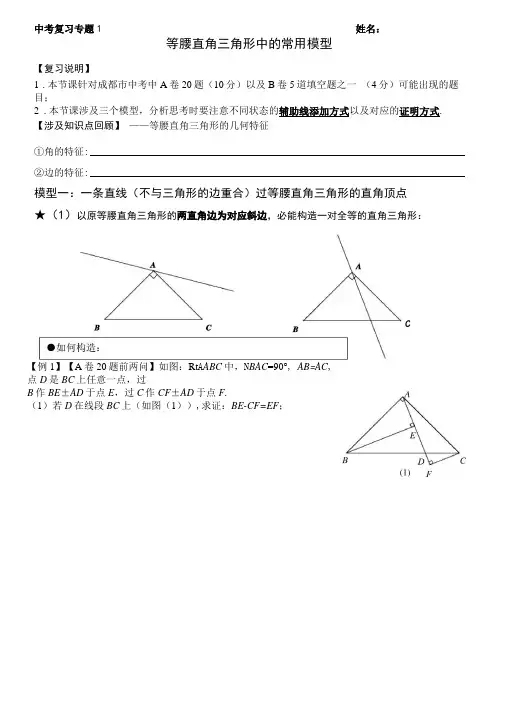
中考复习专题1 姓名：等腰直角三角形中的常用模型【复习说明】1.本节课针对成都市中考中A卷20题（10分）以及B卷5道填空题之一（4分）可能出现的题目；2.本节课涉及三个模型，分析思考时要注意不同状态的辅助线添加方式以及对应的证明方式.【涉及知识点回顾】——等腰直角三角形的几何特征①角的特征: ___________________________________________________________________________②边的特征: ___________________________________________________________________________ 模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点★（1）以原等腰直角三角形的两直角边为对应斜边，必能构造一对全等的直角三角形：C【例1】【A卷20题前两问】如图：Rt A ABC中，N BAC=90°, AB=AC,点D是BC上任意一点，过B作BE±AD于点E，过C作CF±AD于点F.（1）若D在线段BC上（如图（1））,求证：BE-CF=EF；（2）若D在BC的延长线上（如图（2））, （1）中的结论还成立吗？若成立，请说明理由；若不成立，请写出新的结论并证明.【课堂练习1】【B卷填空】如图，等腰RtA ABC中，AB=CB,N ABC=90°,点P在线段BC上（不与B、C重合），以AP为腰作等腰直角4PAQ, QE±AB于E ,连CQ交AB于M.若BPPC则上的值为.MB★（2）以原等腰直角三角形的两直角边为对应直角边，必能构造一对全等的直角三角形:・如何构造:【例2I A卷20题前两问】如图：Rt A ABC中，N BAC=90°, AB=AC, 点D是BC上任意一点，过B作BE±AD于点E，交AC于点G, 过C作CF±AC交AD的延长线与于点F.（1）若D在线段BC上（如图（1））,求证：BG=AF；（2）若D在BC的延长线上（如图（2））, （1）中的结论还成立吗？若成立，请说明理由；若不成立，请写出新的结论并证明.【课堂练习2】【B卷填空】等腰Rt A ABC中，AC=AB,N BAC= 90°,点D、E是AC上两点，且AD=CE, AF±BD于点G，交BC于点F,连接FE并延长，交BD延长线于H.若N ABD=21°, 求N H的度数为°.模型二：等腰直角三角形与另一个直角三角形共斜边★等腰直角三角形与另一个直角三角形有公共斜边，必能以两腰为斜边构造全等三角形・如何构造:•有何特点:【例3】【B 卷填空】等腰Rt A ABC 中，AC=AB , /BAC =90°,±BE 于。

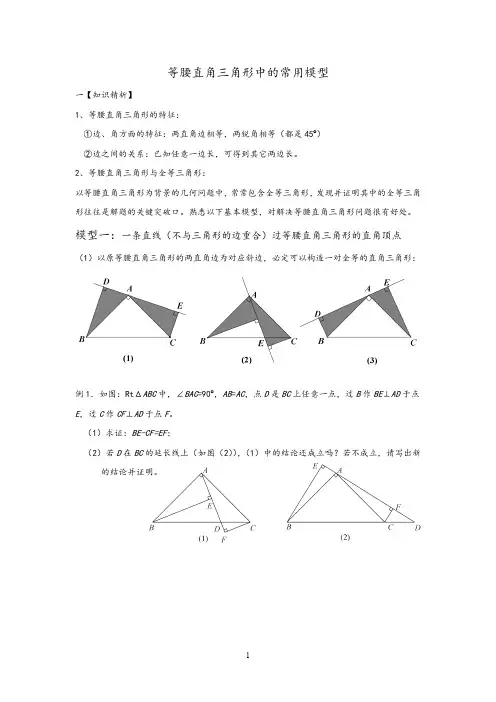
等腰直角三角形中的常用模型一【知识精析】1、等腰直角三角形的特征：①边、角方面的特征：两直角边相等，两锐角相等（都是45º）②边之间的关系：已知任意一边长，可得到其它两边长。

2、等腰直角三角形与全等三角形：以等腰直角三角形为背景的几何问题中，常常包含全等三角形，发现并证明其中的全等三角形往往是解题的关键突破口。

熟悉以下基本模型，对解决等腰直角三角形问题很有好处。

模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点（1）以原等腰直角三角形的两直角边为对应斜边，必定可以构造一对全等的直角三角形：例1．如图：RtΔABC中，∠BAC=90º，AB=AC，点D是BC上任意一点，过B作BE⊥AD于点E，过C作CF⊥AD于点F。

（1）求证：BE-CF=EF；（2）若D在BC的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。

2.如图1，等腰Rt△ABC 中，AB=CB ，∠ABC =90º，点P 在线段BC 上（不与B、C 重合），以AP 为腰长作等腰直角△PAQ ，QE ⊥AB 于E ，连CQ 交AB 于M 。

（1）求证：M 为BE 的中点（2）若PC=2PB，求MBPC的值（2）以原等腰直角三角形的两直角边为对应直角边，必定可以构造一对全等的直角三角形：3、如图：RtΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥AD 于点E ，交AC 于点G ，过C 作CF ⊥AC 交AD 的延长线与于点F 。

（1）求证：BG=AF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。

变式1：如图，在R t△ABC中，∠ACB=45º，∠BAC=90º，AB=AC，点D是AB的中点，AF⊥CD 于H交BC于F，BE∥AC交AF的延长线于E，求证：BC垂直且平分DE.变式2：等腰Rt△ABC中，AC=AB，∠BAC＝90°，点D是AC的中点，AF⊥BD于点E，交BC 于点F，连接DF，求证：∠1=∠2。

列举构造等腰三角形4种常用方法模型
1. 构造等腰三角形的一个底角：
已知等腰三角形的一个底角，我们可以使用圆规和直尺来构造等腰三角形的另一条底边和另一个底角。

2. 利用中垂线构造等腰三角形：
已知线段的中点，我们可以使用中垂线性质来构造等腰三角形。

3. 利用平行线构造等腰三角形：
已知一条直线和该直线外的一点，我们可以使用平行线性质来构造等腰三角形。

4. 利用角平分线性质构造等腰三角形：
已知一个角的角平分线，我们可以使用角平分线性质来构造等腰三角形。

(实用版)等腰直角三角形中的实际应用模型等腰直角三角形是一种具有特殊性质和应用价值的三角形。

在实际生活中，等腰直角三角形的模型被广泛应用于多个领域，包括建筑、工程、地理测量和天文学等等。

建筑领域的应用- 屋顶结构设计：等腰直角三角形的特殊性质使其成为建筑屋顶结构设计中的重要元素。

例如，在典型的尖顶房屋中，等腰直角三角形的形状使其具有良好的结构稳定性和承重能力。

屋顶结构设计：等腰直角三角形的特殊性质使其成为建筑屋顶结构设计中的重要元素。

例如，在典型的尖顶房屋中，等腰直角三角形的形状使其具有良好的结构稳定性和承重能力。

- 建筑布局规划：等腰直角三角形的对称性和刚性特点使其成为建筑布局规划中常用的基本单位。

例如，在城市规划中，可以利用等腰直角三角形构建高效的街道和街区布局模式。

建筑布局规划：等腰直角三角形的对称性和刚性特点使其成为建筑布局规划中常用的基本单位。

例如，在城市规划中，可以利用等腰直角三角形构建高效的街道和街区布局模式。

工程领域的应用- 桥梁设计：等腰直角三角形的稳定性和均匀的压力分布使其成为桥梁设计中的常用形式。

例如，在悬索桥的设计中，等腰直角三角形被广泛应用于桥梁塔台的结构。

桥梁设计：等腰直角三角形的稳定性和均匀的压力分布使其成为桥梁设计中的常用形式。

例如，在悬索桥的设计中，等腰直角三角形被广泛应用于桥梁塔台的结构。

- 测量和计算：等腰直角三角形的特殊关系使其在测量和计算中发挥重要作用。

例如，在三角测量中，可以利用等腰直角三角形的特性来测量远距离和高度。

测量和计算：等腰直角三角形的特殊关系使其在测量和计算中发挥重要作用。

例如，在三角测量中，可以利用等腰直角三角形的特性来测量远距离和高度。

地理测量和天文学中的应用- 方位测量：等腰直角三角形被用于方位测量，即确定一个点相对于一个参考点的方位角。

例如，在地理测量中，可以利用等腰直角三角形和其他测量工具来确定地球上的位置。

方位测量：等腰直角三角形被用于方位测量，即确定一个点相对于一个参考点的方位角。

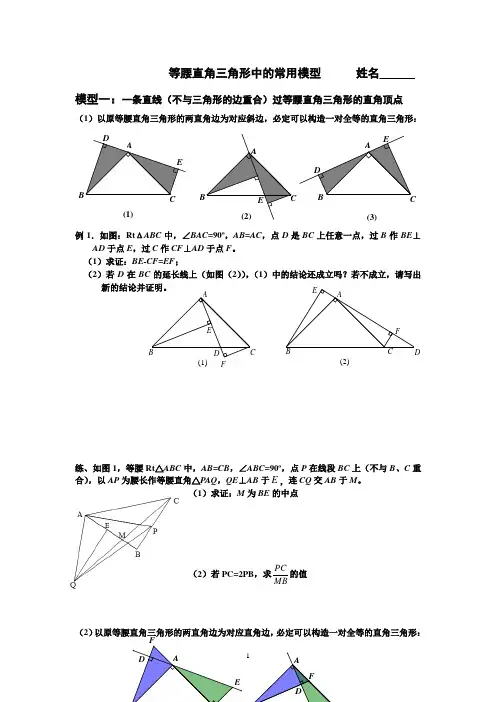
1 等腰直角三角形中的常用模型 姓名______ 模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点
（1）以原等腰直角三角形的两直角边为对应斜边，必定可以构造一对全等的直角三角形：
例1．如图：Rt ΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥
AD 于点E ，过C 作CF ⊥AD 于点F。

（1）求证：BE-CF=EF ；
（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。

练、如图1，等腰Rt △ABC 中，AB=CB ，∠ABC =90º，点P 在线段BC 上（不与B 、C 重合），以AP 为腰长作等腰直角△PAQ ，QE ⊥AB 于E ，连CQ 交AB 于M 。

（1）求证：M 为BE 的中点
（2）若PC=2PB ，求
MB PC 的值
（2）以原等腰直角三角形的两直角边为对应直角边，必定可以构造一对全等的直角三角形： (2)(3)(1)D
D E
E C C E C A B B A A B D F
F
E D A
A (2)F E D C
B A A B
C
D
E
F (1)。

基础版)等腰直角三角形中的基本模型等腰直角三角形是一种特殊的三角形，具有两条边长度相等且与底边垂直的特点。

对于等腰直角三角形，我们可以有一些基本模型来帮助我们理解和解决相关问题。

1.基本定义等腰直角三角形具有以下特点：两条边的长度相等，称为腰；底边与两条腰垂直相交，形成一个直角。

2.边长关系设等腰直角三角形的腰长为 *a*，底边长为 *b*。

由勾股定理可知：a^2 + a^2 = b^2*，即 *2a^2 = b^2*；则 *a = \sqrt{\frac{b^2}{2}}*。

3.高的计算等腰直角三角形的高即为顶点到底边的垂直距离。

根据几何关系可知，高等于腰的一半，即高 *h* 和腰 *a* 的关系为：h = \frac{a}{2}*。

4.面积计算等腰直角三角形的面积可以通过底边长和高的关系来计算，即面积 *S* 和底边长 *b*、高 *h* 的关系为：S = \frac{b \cdot h}{2}*。

5.例题解析例题 1已知等腰直角三角形的底边长为 8 cm，求其面积。

解析：根据高的计算公式，高 *h* 等于底边长的一半，即 *h =\frac{8}{2} = 4*。

代入面积公式可得：S = \frac{8 \cdot 4}{2} = 16*。

所以，等腰直角三角形的面积为 16 平方厘米。

例题 2已知等腰直角三角形的腰长为 6 cm，求其底边长和面积。

解析：根据边长关系公式，底边长 *b* 等于 *a* 的平方根的两倍，即*b = 2 \cdot \sqrt{\frac{6^2}{2}} = 12*。

代入面积公式可得：S = \frac{12 \cdot \frac{6}{2}}{2} = 18*。

所以，等腰直角三角形的底边长为 12 厘米，面积为 18 平方厘米。

6.总结等腰直角三角形是一种特殊的三角形，在解题过程中可以利用基本定义、边长关系、高的计算和面积计算等基本模型来求解相关问题。

通过掌握这些基本模型，我们可以更好地理解和应用等腰直角三角形的概念和性质。

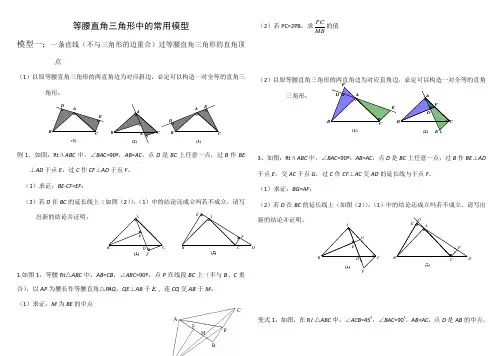
等腰直角三角形中的常用模型模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点（1）以原等腰直角三角形的两直角边为对应斜边，必定可以构造一对全等的直角三角形：例1．如图：Rt ΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE⊥AD 于点E ，过C 作CF ⊥AD 于点F 。

（1）求证：BE-CF=EF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗若不成立，请写出新的结论并证明。

1.如图1，等腰Rt △ABC 中，AB=CB ，∠ABC =90º，点P 在线段BC 上（不与B 、C 重合），以AP 为腰长作等腰直角△PAQ ，QE ⊥AB 于E ，连CQ 交AB 于M 。

（1）求证：M 为BE 的中点（2）若PC=2PB ，求MBPC的值（2）以原等腰直角三角形的两直角边为对应直角边，必定可以构造一对全等的直角三角形：3、如图：Rt ΔABC 中，∠BAC =90º，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥AD 于点E ，交AC 于点G ，过C 作CF ⊥AC 交AD 的延长线与于点F 。

（1）求证：BG=AF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗若不成立，请写出新的结论并证明。

变式1：如图，在R t △ABC 中，∠ACB =45º，∠BAC =90º，AB=AC ，点D 是AB 的中点，GG BACDEF(2)(1)F EDCBADEF FED (2)(1)CCABBA(2)FEDC B AAB C D E F(1)(2)(3)(1)DDEECEAAABAF⊥CD于H交BC于F，BE∥AC交AF的延长线于E，求证：BC垂直且平分DE.变式2：等腰Rt△ABC中，AC=AB，∠BAC＝90°，点D是AC的中点，AF⊥BD于点E，交BC于点F，连接DF，求证：∠1=∠2。