模式识别习题答案

模式识别试卷及答案一、选择题（每题5分，共30分）1. 以下哪一项不是模式识别的主要任务？A. 分类B. 回归C. 聚类D. 预测答案：B2. 以下哪种算法不属于监督学习？A. 支持向量机（SVM）B. 决策树C. K最近邻（K-NN）D. K均值聚类答案：D3. 在模式识别中，以下哪一项是特征选择的目的是？A. 减少特征维度B. 增强模型泛化能力C. 提高模型计算效率D. 所有上述选项答案：D4. 以下哪种模式识别方法适用于非线性问题？A. 线性判别分析（LDA）B. 主成分分析（PCA）C. 支持向量机（SVM）D. 线性回归答案：C5. 在神经网络中，以下哪种激活函数常用于输出层？A. SigmoidB. TanhC. ReLUD. Softmax答案：D6. 以下哪种聚类算法是基于密度的？A. K均值聚类B. 层次聚类C. DBSCAND. 高斯混合模型答案：C二、填空题（每题5分，共30分）1. 模式识别的主要任务包括______、______、______。

答案：分类、回归、聚类2. 在监督学习中，训练集通常分为______和______两部分。

答案：训练集、测试集3. 支持向量机（SVM）的基本思想是找到一个______，使得不同类别的数据点被最大化地______。

答案：最优分割超平面、间隔4. 主成分分析（PCA）是一种______方法，用于降维和特征提取。

答案：线性变换5. 神经网络的反向传播算法用于______。

答案：梯度下降6. 在聚类算法中，DBSCAN算法的核心思想是找到______。

答案：密度相连的点三、简答题（每题10分，共30分）1. 简述模式识别的基本流程。

答案：模式识别的基本流程包括以下几个步骤：（1）数据预处理：对原始数据进行清洗、标准化和特征提取。

（2）模型选择：根据问题类型选择合适的模式识别算法。

（3）模型训练：使用训练集对模型进行训练，学习数据特征和规律。

模式识别考试题答案题1：设有如下三类模式样本集ω1，ω2和ω3，其先验概率相等，求Sw 和Sb ω1：{(1 0)T, (2 0) T, (1 1) T} ω2：{(-1 0)T, (0 1) T, (-1 1) T}ω3：{(-1 -1)T, (0 -1) T, (0 -2) T}解：由于本题中有三类模式，因此我们利用下面的公式：b S =向量类模式分布总体的均值为C ,))()((00031m m m m m P t i i i i --∑=ω,即:i31i i0m )p(E{x }m ∑===ωi m 为第i 类样本样本均值⎪⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+--=⎪⎪⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡---++-=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡++-+-=⎪⎪⎪⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡++++=∑=81628113811381628112181448144811681498149814981498116814481448112131911949119497979797949119491131)m m )(m m ()(P S 919134323131323431m 343121100131m 323211010131m ;313410012131m t0i 0i 31i i b10321ω；333t(i)(i)k k w i i i i i i i i 1i 11111S P()E{(x-m )(x-m )/}C [(x m )(x m )33361211999271612399279Tk ωω====•==--⎡⎤⎡⎤--⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑题2：设有如下两类样本集，其出现的概率相等： ω1：{(0 0 0)T , (1 0 0) T , (1 0 1) T , (1 1 0) T}ω2：{(0 0 1)T , (0 1 0) T , (0 1 1) T , (1 1 1) T}用K-L 变换，分别把特征空间维数降到二维和一维，并画出样本在该空间中的位置。

一、填空与选择填空（本题答案写在此试卷上，30分）1、模式识别系统的基本构成单元包括：模式采集、特征提取与选择和模式分类。

2、统计模式识别中描述模式的方法一般使用特真矢量；句法模式识别中模式描述方法一般有串、树、网。

3、聚类分析算法属于（1）；判别域代数界面方程法属于（3）。

（1）无监督分类 (2)有监督分类（3）统计模式识别方法（4）句法模式识别方法4、若描述模式的特征量为0-1二值特征量，则一般采用（4）进行相似性度量。

（1）距离测度（2）模糊测度（3）相似测度（4）匹配测度5、下列函数可以作为聚类分析中的准则函数的有（1）（3）（4）。

（1）（2） (3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在（2）中进行。

（1）二维空间（2）一维空间（3）N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有（1）；线性可分、不可分都适用的有（3）。

（1）感知器算法（2）H-K算法（3）积累位势函数法8、下列四元组中满足文法定义的有（1）（2）（4）。

（1）({A, B}, {0, 1}, {A?01, A? 0A1 , A? 1A0 , B?BA , B? 0}, A)（2）({A}, {0, 1}, {A?0, A? 0A}, A)（3）({S}, {a, b}, {S ? 00S, S ? 11S, S ? 00, S ? 11}, S)（4）({A}, {0, 1}, {A?01, A? 0A1, A? 1A0}, A)二、(15分)简答及证明题（1）影响聚类结果的主要因素有那些？（2）证明马氏距离是平移不变的、非奇异线性变换不变的。

答：（1）分类准则，模式相似性测度，特征量的选择，量纲。

（2）证明：(2分)(2分)(1分)设，有非奇异线性变换：(1分)(4分)三、(8分)说明线性判别函数的正负和数值大小在分类中的意义并证明之。

答：（1）（4分）的绝对值正比于到超平面的距离平面的方程可以写成式中。

模式识别答案模式识别试题⼆答案问答第1题答：在模式识别学科中，就“模式”与“模式类”⽽⾔，模式类是⼀类事物的代表，概念或典型，⽽“模式”则是某⼀事物的具体体现，如“⽼头”是模式类，⽽王先⽣则是“模式”，是“⽼头”的具体化。

问答第2题答：Mahalanobis距离的平⽅定义为：其中x，u为两个数据，是⼀个正定对称矩阵（⼀般为协⽅差矩阵）。

根据定义，距某⼀点的Mahalanobis距离相等点的轨迹是超椭球，如果是单位矩阵Σ，则Mahalanobis距离就是通常的欧⽒距离。

问答第3题答：监督学习⽅法⽤来对数据实现分类，分类规则通过训练获得。

该训练集由带分类号的数据集组成，因此监督学习⽅法的训练过程是离线的。

⾮监督学习⽅法不需要单独的离线训练过程，也没有带分类号（标号）的训练数据集，⼀般⽤来对数据集进⾏分析，如聚类，确定其分布的主分量等。

就道路图像的分割⽽⾔，监督学习⽅法则先在训练⽤图像中获取道路象素与⾮道路象素集，进⾏分类器设计，然后⽤所设计的分类器对道路图像进⾏分割。

使⽤⾮监督学习⽅法，则依据道路路⾯象素与⾮道路象素之间的聚类分析进⾏聚类运算，以实现道路图像的分割。

问答第4题答：动态聚类是指对当前聚类通过迭代运算改善聚类；分级聚类则是将样本个体，按相似度标准合并，随着相似度要求的降低实现合并。

问答第5题答：在给定观察序列条件下分析它由某个状态序列S产⽣的概率似后验概率，写成P(S|O)，⽽通过O求对状态序列的最⼤似然估计,与贝叶斯决策的最⼩错误率决策相当。

问答第6题答：协⽅差矩阵为，则1）对⾓元素是各分量的⽅差，⾮对⾓元素是各分量之间的协⽅差。

2）主分量，通过求协⽅差矩阵的特征值，⽤得，则，相应的特征向量为：，对应特征向量为，对应。

这两个特征向量即为主分量。

3） K-L变换的最佳准则为：对⼀组数据进⾏按⼀组正交基分解，在只取相同数量分量的条件下，以均⽅误差计算截尾误差最⼩。

4）在经主分量分解后，协⽅差矩阵成为对⾓矩阵，因⽽各主分量间相关消除。

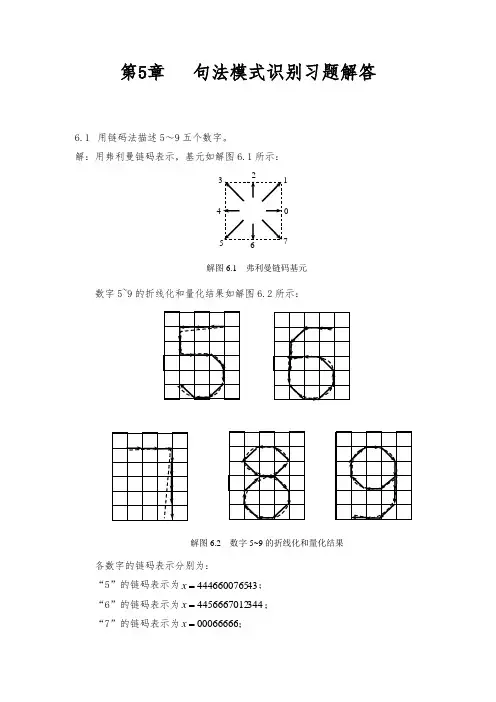
第5章 句法模式识别习题解答6.1 用链码法描述5～9五个数字。

解：用弗利曼链码表示，基元如解图6.1所示：数字5~9的折线化和量化结果如解图6.2所示：各数字的链码表示分别为：“5”的链码表示为434446600765=x ； “6”的链码表示为3444456667012=x ； “7”的链码表示为00066666=x ；0 17解图6.1 弗利曼链码基元解图6.2 数字5~9的折线化和量化结果“8”的链码表示为21013457076543=x ； “9”的链码表示为5445432107666=x 。

6.2 定义所需基本基元，用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。

解：设基元为：用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=；“K ”的链描述为))((b a d d x K ⨯⨯+=； “Z ”的链描述为))((c c g x Z ⨯-=。

6.3 设有文法),,,(S P V V G T N =，N V ，T V 和P 分别为},,{B A S V N =，},{b a V T =：P ①aB S →，②bA S →，③a A →，④aS A →⑤bAA A →，⑥b B →，⑦bS B →，⑧aBB B → 写出三个属于)(G L 的句子。

解：以上句子ab ，abba ，abab ，ba ，baab ，baba 均属于)(G L 。

bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③6.4 设有文法),,,(S P V V G T N =，其中},,,{C B A S V N =，}1,0{=T V ，P 的各生成式为①A S 0→，②B S 1→，③C S 1→ ④A A 0→，⑤B A 1→，⑥1→A ⑦0→B ，⑧B B 0→，⑨C C 0→，⑩1→C问00100=x 是否属于语言)(G L ？ 解：由可知00100=x 属于语言)(G L 。

模式识别习题及答案模式识别习题及答案模式识别是人类智能的重要组成部分，也是机器学习和人工智能领域的核心内容。

通过模式识别，我们可以从大量的数据中发现规律和趋势，进而做出预测和判断。

本文将介绍一些模式识别的习题，并给出相应的答案，帮助读者更好地理解和应用模式识别。

习题一：给定一组数字序列，如何判断其中的模式？答案：判断数字序列中的模式可以通过观察数字之间的关系和规律来实现。

首先，我们可以计算相邻数字之间的差值或比值，看是否存在一定的规律。

其次，我们可以将数字序列进行分组，观察每组数字之间的关系，看是否存在某种模式。

最后，我们还可以利用统计学方法，如频率分析、自相关分析等，来发现数字序列中的模式。

习题二：如何利用模式识别进行图像分类？答案：图像分类是模式识别的一个重要应用领域。

在图像分类中，我们需要将输入的图像分为不同的类别。

为了实现图像分类，我们可以采用以下步骤：首先，将图像转换为数字表示，如灰度图像或彩色图像的像素矩阵。

然后，利用特征提取算法，提取图像中的关键特征。

接下来，选择合适的分类算法，如支持向量机、神经网络等，训练模型并进行分类。

最后，评估分类结果的准确性和性能。

习题三：如何利用模式识别进行语音识别？答案：语音识别是模式识别在语音信号处理中的应用。

为了实现语音识别，我们可以采用以下步骤：首先，将语音信号进行预处理，包括去除噪声、降低维度等。

然后，利用特征提取算法，提取语音信号中的关键特征，如梅尔频率倒谱系数（MFCC）。

接下来，选择合适的分类算法，如隐马尔可夫模型（HMM）、深度神经网络（DNN）等，训练模型并进行语音识别。

最后，评估识别结果的准确性和性能。

习题四：如何利用模式识别进行时间序列预测？答案：时间序列预测是模式识别在时间序列分析中的应用。

为了实现时间序列预测，我们可以采用以下步骤：首先，对时间序列进行平稳性检验，确保序列的均值和方差不随时间变化。

然后，利用滑动窗口或滚动平均等方法，将时间序列划分为训练集和测试集。