弹性变形与非弹性变形
- 格式:doc
- 大小:332.50 KB
- 文档页数:3


挂篮变形计算
1、挂篮变形包括:桁架弹性变形、前吊带弹性变形、非弹性变形。
2、桁架变形计算:将桁架简化为铰接形式,按各个梁段的不同重量,分别计算其弹性变形。
3、前吊带变形计算:将底模架前横梁简化为弹性支承的连续梁,根据各个梁段的实际荷载计算各个支承的受力,然后根据受力情况计算出吊带的变形量。
4、非弹性变形测试:挂篮的非弹性变形由挂篮试压试验来实测,对于未经试压的挂篮,参考已试压挂篮(各套挂篮为同一型号、同一工厂、同一工艺加工)的变形值在第一次挂篮施工时设置,对于已试压的挂篮认为非弹性变形已消除在施工时,不再考虑。
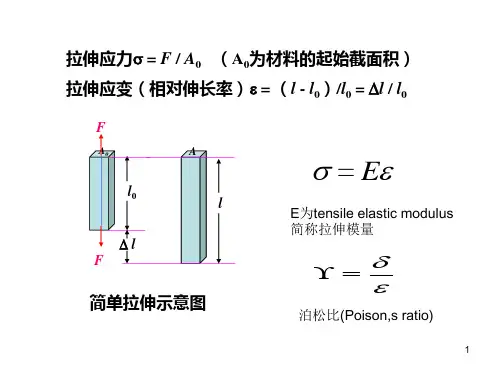

应变(strain):为一微小材料(元素)承受应力时所产生的单位长度变形量(力学定义,无量纲)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形.重要特征:可逆性、胡克定律(是力学基本定律之一。
适用于一切固体材料的弹性定律,它指出:在弹性限度内,物体的形变跟引起形变的外力成正比)4)塑性变形(plastic deformation):材料在外力作用下产生的永久不可恢复的变形。
(5)断裂(fracture,rupture 破裂、crack裂纹):物体在外力作用下产生裂纹以至断开的现象.脆性断裂(未发生较明显的塑性变形)、韧性断裂(发生较明显的塑性变形),宏观特征(1)弹性(elasticity):是指物体(材料)本身的一种特性,发生形变后可以恢复原来的状态的一种性质.(2)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
(3)弹性模量(elastic modulus,modulus of elasticity):是表征材料弹性的物理参数,是指材料在弹性变形范围内,应力和对应的应变的比值E=σ/ε,也是材料内部原子之间结合力强弱的直接量度。
(4)刚度(stiffness):指物体(固体)在外力作用下抵抗变形的能力,可用使产生单位形变所需的外力值来量度。
刚度越高,物体表现越硬。
(5)弹性比功(elastic specific work):表示材料吸收弹性变形功的能力,弹性比能、应变比能,决定于弹性模量和弹性极限(即材料由弹性变形过渡到弹—塑性变形时的应力).(6)滞弹性(anelasticity):在弹性范围内加快加载或卸载后,随时间延长产生附加弹性应变的现象.7)循环弹性(cyclic elasticity):在交变载荷(振动)下材料吸收不可逆变形功的能力。

《弹性碰撞和非弹性碰撞》碰撞前后变化在我们日常生活和物理学的研究中,碰撞是一种常见的现象。
而碰撞又分为弹性碰撞和非弹性碰撞,它们在碰撞前后会产生不同的变化。
首先,我们来了解一下什么是弹性碰撞。
弹性碰撞是指在碰撞过程中,系统的机械能守恒,也就是说碰撞前后系统的总动能保持不变。
想象一下两个质量相等的小球,一个静止,另一个以一定的速度撞向静止的那个。
在弹性碰撞的情况下,碰撞后,原来运动的小球会停下来,而原来静止的小球会以原来运动小球的速度向前运动。
这种碰撞就如同两个充满弹性的皮球相互碰撞,它们在碰撞后能完全恢复原来的形状和能量。
弹性碰撞的特点十分显著。
一是碰撞前后系统的总动能不变。
这意味着在计算碰撞前后物体的速度时,我们可以通过动能守恒定律来准确地得出结果。
二是碰撞前后系统的动量也守恒。
动量是物体质量和速度的乘积,在弹性碰撞中,总动量始终保持不变。
三是碰撞过程中,物体之间的相互作用力是保守力,这使得能量在转化过程中没有损失。
我们通过一个简单的例子来更直观地感受弹性碰撞。
假设在一个光滑的水平面上,有两个质量分别为 m1 和 m2 的小球,它们的速度分别为 v1 和 v2 。
在发生弹性碰撞后,它们的速度分别变为 v1' 和 v2' 。
根据弹性碰撞的规律,我们可以通过一系列的公式计算出碰撞后的速度。
这不仅在理论上有重要意义,在实际的物理实验和工程应用中也有很大的价值。
接下来,我们看看非弹性碰撞。
非弹性碰撞与弹性碰撞最大的不同在于,在碰撞过程中,系统的机械能不守恒,会有一部分机械能转化为其他形式的能量,比如内能。
这就好像两个橡皮泥球撞在一起,它们会粘在一起或者发生变形,无法完全恢复原来的状态,从而导致能量的损失。
非弹性碰撞也有其自身的特点。
首先,碰撞后系统的总动能会减少。
这部分减少的动能通常转化为物体的内能,使得物体的温度升高或者产生其他形式的能量损耗。
其次,虽然总动量仍然守恒,但由于动能的损失,计算碰撞后的速度就变得相对复杂。





工程力学中的弹性变形和塑性变形工程力学是研究物体力学性质和运动规律的学科,其中弹性变形和塑性变形是重要的概念。
本文将就工程力学中的弹性变形和塑性变形进行探讨,介绍它们的定义、特点以及在工程实践中的应用等方面。
一、弹性变形在工程力学中,当物体受到外力作用后发生形状和尺寸的变化,但当外力消失时,物体又能够恢复到原来的形状和尺寸,这种变形称为弹性变形。
在弹性变形的过程中,物体内部的分子、原子和离子之间的相互作用力起着决定性的作用。
弹性变形具有以下几个特点:1. 可逆性:弹性变形是不可逆的,一旦外力消失,物体会恢复到原来的形状和尺寸。
2. 线性弹性:弹性变形遵循胡克定律,即外力与物体变形之间存在线性关系,变形量与外力成正比。
3. 加载-卸载路径无关性:在弹性变形过程中,物体的变形与加载-卸载路径无关,只与物体的弹性特性有关。
弹性变形在工程实践中具有广泛的应用,例如弹簧、橡胶材料、结构设计等领域。
通过研究物体的弹性特性,可以预测和计算物体在受力作用下的变形和应力分布,为工程设计提供依据。
二、塑性变形与弹性变形相对应,塑性变形是指物体在受到外力作用后,即使外力消失,物体也无法完全恢复到原来的形状和尺寸。
塑性变形发生时,物体内部的分子、原子和离子之间发生永久性的移动和重新排列。
塑性变形具有以下几个特点:1. 不可逆性:塑性变形是不可逆的,一旦物体发生塑性变形,即使外力消失,物体也无法完全恢复到原来的状态。
2. 非线性塑性:塑性变形遵循非线性本构关系,即变形量与外力不成线性关系。
3. 加载-卸载路径有关性:塑性变形与加载-卸载路径有关,不同的变形路径会导致不同的变形和应力分布。
塑性变形在工程实践中也具有广泛的应用,例如金属加工、塑料成型、土壤力学等领域。
研究物体的塑性特性可以帮助工程师了解材料的强度、可塑性以及在受力情况下的变形规律,并进行相应的结构设计和材料选择。
总结工程力学中的弹性变形和塑性变形是两个重要的概念,对于了解物体在受力作用下的变形规律和应力分布具有重要意义。
塑性变形和弹性变形的区别是什么
形变是物体由于外因或内在缺陷,在外力作用下物质的各部分的相对位置发生变化的过程。
接下来,为大家详细说下什么是弹性形变和塑性形变和塑性变形和弹性变形的区别。
一、什么是弹性形变和塑性形变
弹性形变是指固体受外力作用而使各点间相对位置的改变,当外力撤消后,固体又恢复原状谓之“弹性形变”。
如果外力较大,当它的作用停止时,所引起的形变并不完全消失,而有剩余形变,称为塑性形变。
二、塑性变形和弹性变形的区别
1、性质不同
弹性变形为可逆变形,其数值大小与外力成正比,其比例系数称为弹性模量,材料在弹性变形范围内,弹性模量为常数。
而塑性变形为不可逆变形,工程材料及构件受载超过弹性变形范围之后将发生永
久的变形,即卸除载荷后将出现不可恢复的变形,或称残余变形。
2、概念不同
物体受外力作用时,就会产生变形,如果将外力去除后,物体能够完全恢复它原来的形状和尺寸,这种变形称为弹性变形。
材料在外力作用下产生形变,而在外力去除后,弹性变形部分消失,不能恢复而保留下来的的那部分变形即为塑性变形。
3、相关性质物体不同
金属、塑料等都具有不同程度的塑性变形能力,故可称为塑性材料。
玻璃、陶瓷、石墨等脆性材料则无塑性变形能力。
除外力能产生弹性变形外,晶体内部畸变也能在小范围内产生弹性变形,如空位、间隙原子、位错、晶界等晶体缺陷周围,由于原子排列不规则而存在弹性变形。
夹杂物和第二相周围也可能存在弹性变形。
物理弹性碰撞与非弹性碰撞的区别知识点在我们的日常生活中,碰撞这个现象简直无处不在。
从小朋友们玩的弹球,到马路上车辆的追尾,甚至是宇宙中天体的相互作用,都涉及到碰撞。
而在物理学中,碰撞被分为了弹性碰撞和非弹性碰撞。
这俩家伙的区别,可有着不少门道呢!咱先来说说弹性碰撞。
弹性碰撞就像是两个超级有弹性的“弹簧人”撞在了一起。
比如说,你拿两个质量相同的皮球,让它们以相同的速度正面碰撞。
在碰撞的那一瞬间,你会发现它们就像两个调皮的小精灵,互相碰了一下之后,立马弹开,而且速度的大小和方向都跟碰撞前完全相反。
不仅如此,它们的动能在碰撞前后也一点儿都没损失,就像是能量被完好地保存在了一个神奇的能量盒子里,一点儿都没跑掉。
我记得有一次,我和小伙伴在公园里玩,就做了一个类似弹性碰撞的小实验。
我们找了两根长长的竹子,把它们当成“撞杆”。
然后,我和小伙伴分别站在竹子的两端,用力把竹子往中间推。
当两根竹子碰撞在一起的时候,那种反弹的力量真的让我感觉到了弹性碰撞的神奇。
竹子瞬间弹回,就好像它们根本不想碰到对方,只想赶紧回到原来的位置。
这时候,我们能明显感觉到,在碰撞的过程中,力量被完美地传递和反弹,没有任何的损耗。
再说说非弹性碰撞,这可就有点不一样啦。
非弹性碰撞就像是两个不太灵活的“小胖子”撞在了一起,然后就黏糊在了一块儿,或者是有一部分能量悄悄地跑掉了。
比如说,一辆汽车撞到了一堵墙上,车停下来了,但是车的一部分动能就转化成了车辆的变形、摩擦产生的热能等等,这些能量可就再也回不来了。
我想起有一回在路上看到的一场小车祸。
一辆小轿车不小心追尾了一辆面包车。
那“砰”的一声巨响,可把周围的人都吓了一跳。
等大家围过去看的时候,发现小轿车的车头凹进去了一大块,面包车的车尾也有不少损伤。
这明显就是非弹性碰撞啊!两车碰撞之后,速度都发生了很大的变化,而且有很多能量都被用来造成车辆的损坏了,这些能量一去不复返,真是让人心疼那些浪费掉的能量。
弹性碰撞和非弹性碰撞在实际生活中的应用也特别多。
应变(strain):为一微小材料(元素)承受应力时所产生的单位长度变形量(力学定义,无量纲)弹性变形(elastic deformation): 材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
重要特征:可逆性、胡克定律(是力学基本定律之一。
适用于一切固体材料的弹性定律,它指出:在弹性限度内,物体的形变跟引起形变的外力成正比)4)塑性变形(plastic deformation):材料在外力作用下产生的永久不可恢复的变形。
(5)断裂(fracture,rupture 破裂、crack裂纹):物体在外力作用下产生裂纹以至断开的现象。
脆性断裂(未发生较明显的塑性变形)、韧性断裂(发生较明显的塑性变形),宏观特征(1)弹性(elasticity):是指物体(材料)本身的一种特性,发生形变后可以恢复原来的状态的一种性质。
(2)弹性变形(elastic deformation):材料在外力作用下产生变形,当外力去除后恢复其原来形状,这种随外力消失而消失的变形。
(3)弹性模量(elastic modulus,modulus of elasticity):是表征材料弹性的物理参数,是指材料在弹性变形范围内,应力和对应的应变的比值E=σ/ε,也是材料内部原子之间结合力强弱的直接量度。
(4)刚度(stiffness):指物体(固体)在外力作用下抵抗变形的能力,可用使产生单位形变所需的外力值来量度。
刚度越高,物体表现越硬。
(5)弹性比功(elastic specific work):表示材料吸收弹性变形功的能力,弹性比能、应变比能,决定于弹性模量和弹性极限(即材料由弹性变形过渡到弹-塑性变形时的应力)。
(6)滞弹性(anelasticity):在弹性范围内加快加载或卸载后,随时间延长产生附加弹性应变的现象。
7)循环弹性(cyclic elasticity):在交变载荷(振动)下材料吸收不可逆变形功的能力。
弹性和非弹性碰撞:弹性碰撞和非弹性碰撞的区别与解释弹性碰撞和非弹性碰撞是物理学中两个重要的概念,用来描述两个物体之间的相互作用过程。
两种碰撞方式有着明显的区别,下面将对弹性碰撞和非弹性碰撞进行解释和比较。
首先,弹性碰撞是指两个物体之间相互撞击后彼此分离,并且能够恢复到碰撞前的形状和能量状态。
在弹性碰撞过程中,动量和能量守恒定律成立,碰撞前的动量和能量等于碰撞后的动量和能量。
弹性碰撞可以看作是物体之间弹性力作用下的相互作用过程。
相比之下,非弹性碰撞则是指两个物体碰撞后不能完全分离,且在碰撞过程中会发生能量的转化和损失。
在非弹性碰撞中,动量守恒定律仍然成立,但能量守恒定律不再成立。
通常在非弹性碰撞中,能量会转化为其他形式,比如热能或声能,而且有一部分能量会损失。
弹性碰撞和非弹性碰撞的区别主要体现在能量的守恒和物体的形状变化上。
在弹性碰撞中,碰撞后的两个物体能够恢复到碰撞前的状态,即形状不变且没有能量的损失。
而在非弹性碰撞中,碰撞后的物体形状通常会发生变化,并且能量会损失。
弹性碰撞和非弹性碰撞的实际应用有很多。
弹性碰撞常常出现在球类运动中,比如乒乓球、网球等。
当球与球碰撞时,通常会发生弹性碰撞,碰撞后球的形状不会发生变化,同时能量也会保持不变。
非弹性碰撞常常出现在汽车碰撞等情况中。
当车辆发生碰撞时,车身会发生形变,并且会有能量损失。
弹性碰撞和非弹性碰撞都是现实中非常普遍的碰撞形式,我们需要根据不同情况进行合理的模型选择和计算。
在弹性碰撞中,我们可以利用动量和能量守恒定律进行计算,而非弹性碰撞由于能量损失,常常需要考虑其他因素,比如形变和能量转化等。
总之,弹性碰撞和非弹性碰撞是物体之间相互作用的两种不同形式。
弹性碰撞中物体形状不变,能量守恒;而非弹性碰撞中物体形状发生变化,能量不守恒。
我们需要根据具体情况选择合适的模型和方法进行计算和研究。
碰撞是物理学中一个重要的研究领域,研究物体之间的相互作用以及碰撞前后的状态变化。
第四章岩石的变形一、基本概念1、岩石变形的定义:岩石变形:指岩石在任何物理因素作用下形状和大小的变化。
工程上的岩石变形是指在外力作用下引起的形状和大小的变化。
变形类型:弹性变形、塑性变形、粘性变形。
①弹性变形:是指材料在外力的作用下发生变形并在外力撤去后立即恢复到它原有的形状和尺寸的性质。
把外力撤去后能够恢复的变形称为弹性变形。
线弹性:应力——应变关系呈直线关系。
非线性:应力——应变关系呈曲线关系(或完全弹性)。
②塑性变形:是指材料受力后,在应力超过屈服应力时仍能继续变形而不即行断裂,撤去外力后,变形又不能完全恢复的性质。
不能恢复的变形为塑性变形(永久变形)。
应力达屈服应力后转为塑性变形。
③粘性:指材料受力后变形不能在瞬间完成,切应变的速率随应力的大小而改变的性质。
应变速率随应力而变化的变形称为流变(流动变形)。
二、岩石变形的力学参数1、弹性模量线弹性:非线弹性:定义几个弹性模量:①初始弹性模量Ei应力为零时的曲线斜率,即②切线弹性模量Et Array曲线上任一点的斜率,即E③平均弹性模量av曲线上近于直线段的斜率。
④割线弹性模量ES曲线原点与曲线上任一点连线的斜率。
2、泊松比3、剪切模量4、拉梅常数:5、体积弹性模量:其中:)(31z y x m σσσσ++=z y x v VVεεεε++≈∆=6、卸载模量卸载曲线的割线斜率。
平均弹性模量w E ,与割线的斜率卸载模量代替弹性模量。
7、变形模量变形模量为总变形量与平均应力的比值。
对于弹塑性岩石,其变形由弹性变形和塑性变形组成则变形模量是描述岩石的总体变形。
三、岩石变形的基本特征1、变形阶段由岩石变形曲线的变化特征,可分为四个阶段:1) 0~A 段,为弹性阶段 应力 — 轴向应变(y σσ~)曲线微呈上凹形,即由初始弹性模量变到平均弹模。
2)A ~B 段,为弹性阶段应力—轴向应变曲线接近于直线,其弹性模量为常数,等于直线的斜率,即平均弹性模量av E 。