数理统计之回归分析基础
- 格式:pdf
- 大小:552.76 KB
- 文档页数:34


北京市农业经济总产值的逐步回归分析姓名:学号:摘要:农业生产和农村经济是国民经济的基础,影响农村经济总产值的因素有多种,主要包括农林牧渔业。
本文以北京市农业生产和农村经济总产值为对象,首先分析了各种因素的线性相关性,建立回归模型,再利用逐步回归法进行回归分析,得到最符合实际情况的回归模型。
以SPSS 17.0为分析工具,给出了实验结果,并用预测值验证了结论的正确性。
关键词:农业生产和农村经济,线性回归模型,逐步回归分析,SPSS1.引言农林牧渔业统计范围包括辖区内全部农林牧渔业生产单位、非农行业单位附属的农林牧渔业生产活动单位以及农户的农业生产活动。
军委系统的农林牧渔业生产(除军马外)也应包括在内,但不包括农业科学试验机构进行的农业生产。
在近几年中国经济快速增长的带动下,各地区农林牧渔业也得到了突飞猛进的发展。
以北京地区为例,2005年的农业总产值为1993年的6倍。
因此用统计方法研究分析农业总产值对指导国民经济生产,合理有效的进行产业布局,提高生产力等有着重要意义。
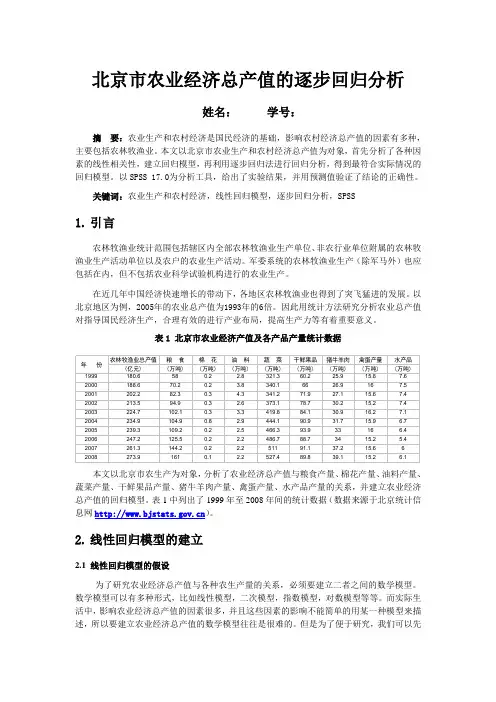
表1 北京市农业经济产值及各产品产量统计数据本文以北京市农生产为对象,分析了农业经济总产值与粮食产量、棉花产量、油料产量、蔬菜产量、干鲜果品产量、猪牛羊肉产量、禽蛋产量、水产品产量的关系,并建立农业经济总产值的回归模型。
表1中列出了1999年至2008年间的统计数据(数据来源于北京统计信息网)。
2.线性回归模型的建立2.1 线性回归模型的假设为了研究农业经济总产值与各种农生产量的关系,必须要建立二者之间的数学模型。
数学模型可以有多种形式,比如线性模型,二次模型,指数模型,对数模型等等。
而实际生活中,影响农业经济总产值的因素很多,并且这些因素的影响不能简单的用某一种模型来描述,所以要建立农业经济总产值的数学模型往往是很难的。
但是为了便于研究,我们可以先假定一些前提条件,然后在这些条件下得到简化后的近似模型。
以下我们假定两个前提条件:1) 农产品的价格是不变的。

回归分析有哪些基本的步骤回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析也有一定的步骤。
以下是由店铺整理回归分析的内容,希望大家喜欢!回归分析的简介①从一组数据出发,确定某些变量之间的定量关系式,即建立数学模型并估计其中的未知参数。
估计参数的常用方法是最小二乘法。
②对这些关系式的可信程度进行检验。
③在许多自变量共同影响着一个因变量的关系中,判断哪个(或哪些)自变量的影响是显著的,哪些自变量的影响是不显著的,将影响显著的自变量入模型中,而剔除影响不显著的变量,通常用逐步回归、向前回归和向后回归等方法。
④利用所求的关系式对某一生产过程进行预测或控制。
回归分析的应用是非常广泛的,统计软件包使各种回归方法计算十分方便。
在回归分析中,把变量分为两类。
一类是因变量,它们通常是实际问题中所关心的一类指标,通常用Y表示;而影响因变量取值的的另一类变量称为自变量,用X来表示。
回归分析研究的主要问题是:(1)确定Y与X间的定量关系表达式,这种表达式称为回归方程;(2)对求得的回归方程的可信度进行检验;(3)判断自变量X对因变量Y有无影响;(4)利用所求得的回归方程进行预测和控制。
回归分析的应用相关分析研究的是现象之间是否相关、相关的方向和密切程度,一般不区别自变量或因变量。
而回归分析则要分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系。
比如说,从相关分析中我们可以得知“质量”和“用户满意度”变量密切相关,但是这两个变量之间到底是哪个变量受哪个变量的影响,影响程度如何,则需要通过回归分析方法来确定。
一般来说,回归分析是通过规定因变量和自变量来确定变量之间的因果关系,建立回归模型,并根据实测数据来求解模型的各个参数,然后评价回归模型是否能够很好的拟合实测数据;如果能够很好的拟合,则可以根据自变量作进一步预测。
例如,如果要研究质量和用户满意度之间的因果关系,从实践意义上讲,产品质量会影响用户的满意情况,因此设用户满意度为因变量,记为Y;质量为自变量,记为X。

第七章回归分析前几章所讨论的内容,其目的在于寻求被测量的最佳值及其精度。
在生产和科学实验中,还有另一类问题,即测量与数据处理的目的并不在于获得被测量的估计值,而是为了寻求两个变量或多个变量之间的内在关系,这就是本章所要解决的主要问题。
表达变量之间关系的方法有散点图、表格、曲线、数学表达式等,其中数学表达式能较客观地反映事物的内在规律性,形式紧凑,且便于从理论上作进一步分析研究,对认识自然界量与量之间关系有着重要意义。
而数学表达式的获得是通过回归分析方法完成的。
第一节回归分析的基本概念一、函数与相关在生产和科学实验中,人们常遇到各种变量。
从贬值辩证唯物主义观点来看,这些变量之间是相互联系、互相依存的,它们之间存在着一定的关系。
人们通过实践,发现变量之间的关系可分为两种类型:1.函数关系(即确定性关系)数学分析和物理学中的大多数公式属于这种类型。
如以速度v作匀速运动的物体,走过的距离s与时间t之间,有如下确定的函数关系:s=vt若上式中的变量有两个已知,则另一个就可由函数关系精确地求出。
2.相关关系在实际问题中,绝大多数情况下变量之间的关系不那么简单。
例如,在车床上加工零件,零件的加工误差与零件的直径之间有一定的关系,知道了零件直径可大致估计其加工误差,但又不能精确地预知加工误差。
这是由于零件在加工过程中影响加工误差的因素很多,如毛坯的裕量、材料性能、背吃刀量、进给量、切削速度、零件长度等等,相互构成一个很复杂的关系,加工误差并不由零件直径这一因素所确定。
像这种关系,在实践中是大量存在的,如材料的抗拉强度与其硬度之间;螺纹零件中螺纹的作用中径与螺纹中径之间;齿轮各种综合误差与有关单项误差之间;某些光学仪器、电子仪器等开机后仪器的读数变化与时间之间;材料的性能与其化学成分之间等等。
这些变量之间既存在着密切的关系,又不能由一个(或几个)变量(自变量)的数值精确地求出另一个变量(因变量)的数值,而是要通过试验和调查研究,才能确定它们之间的关系,我们称这类变量之间的关系为相关关系。


统计学中的回归分析方法统计学是一门应用科学,可以帮助我们理解和解释数据。
在统计学中,回归分析是一种常用的方法,用于研究变量之间的关系以及预测未来的趋势。
回归分析是一种基于概率论和数理统计的方法,用于描述和模拟数据的线性关系。
通过回归分析,我们可以确定一个或多个自变量与因变量之间的数学关系。
这使得我们能够根据已有的数据预测未来的趋势和结果。
回归分析的核心概念是回归方程。
回归方程是用于描述自变量与因变量之间关系的数学公式。
在简单线性回归中,回归方程可以用y = a+ bx来表示,其中y是因变量,x是自变量,a和b是回归方程的参数。
通过回归方程,我们可以计算自变量对因变量的影响程度。
回归的目标是找到最适合数据的回归方程,并通过该方程对未知数据做出预测。
回归分析有不同的类型。
简单线性回归是最基本的形式,用于研究两个变量之间的关系。
多元线性回归则用于研究多个自变量对因变量的影响。
此外,还有逻辑回归用于处理二元分类问题,和多项式回归适用于非线性关系。
回归分析还可以帮助我们评估各个变量对因变量的相对重要性。
通过计算回归方程中各个参数的显著性,我们可以确定哪些自变量对因变量的影响更为显著。
在回归分析中,误差的处理也是非常重要的。
误差代表了回归模型无法解释的数据波动。
最小二乘法是一种常用的方法,用于最小化回归模型的总体误差。
除了简单的回归分析,还有一些衍生的方法可以扩展回归模型的适用范围。
岭回归和Lasso回归是用于应对多重共线性问题的方法。
弹性网络回归则是将岭回归和Lasso回归进行结合,取两种方法的优点。
回归分析在许多领域都有广泛的应用。
在经济学中,回归分析常用于研究经济指标之间的关系。
在市场营销中,回归模型可以用于预测销量和分析市场趋势。
在医学研究中,回归分析可以帮助研究人员研究疾病和治疗方法之间的关系。
总之,统计学中的回归分析是一种强大的工具,用于研究变量之间的关系和预测未来的趋势。
通过回归分析,我们可以理解数据并做出有意义的预测。

数理统计分析知识及回归分析方法把研究对象的全体称为总体,构成总体的每个单位称为 个体,通常用N 表示总体所包含的个体数。
总体的一部分称 为样本(或成子样),通常用n 表示样本所含的个体数,称 为样本容量。
从总体中抽区样本称为抽样。
若总体中每个个体被抽取的可能性相同,这样的抽样称为随机抽样,所获得的样本称 为随机样本。
在许多情况下不可能直接试验或研究总体,例如灯泡的 寿命、混凝土强度等,总是采用抽样的方法,通过试验或研 究样品的特性,去估计该批产品的特性或质量状况。
数理统 计就是一种以概率论为理论基础、 通过研究随机样本(样品) 对总体的特性或质量状况作出估计和评价的方法。
对于工程试验中常见的正态分布,主要计算样本的三个 统计量,即平均值、标准差(或极差)和变异系数。
一、样本平均值:以算术平均值 X 表示,可按下式计xi式中:xi ——各个试验数据试验数据个数nxi各个试验数据之和、样本标准差:以标准差s表示,可按下式计算:xi上式又称贝塞尔公式。
标准差表示一组试验数据对于其平均值的离散程度,也就是数据的波动情况,具有与平均值相同的量纲。
在相同平均值条件下,标准差大表示数据离散程度大,即波动大;标准差小表示数据离散程度小,波动小三、样本极差:极差也可以表示数据的离散程度。
极差是数据中最大值与最小值之差:极差也可以表示数据的离散程度。
极差是数据中最大值与最小值之差:当一批数据不多时(n W 10),可用样本极差估计总体标准差:A式中::标准差的估计值;R :极差;dn:与n有关的系数,一般,dn可近似地取为:X max x mins1ni 1,2< n W 10四、样本变异系数:变异系数表示数据的相对波动大小,按下式表示:sC v 100%x数据的性Cv可用于不同平均制条件下数据饿波动情况,更能反映质。
回归分析回归分析是一重处理变量与变量之间关系的数学方法。
变量与变量之间存在对应关系的,称为函数关系。


数理统计的基本原理和方法数理统计是一门研究数据收集、整理、分析和解释的学科,它在各个领域都发挥着重要的作用。
本文将介绍数理统计的基本原理和方法,包括样本与总体、数据的描述统计、概率分布、假设检验和回归分析等内容。
一、样本与总体在进行统计分析的过程中,我们常常需要从整个数据集中选取一部分作为样本进行研究。
样本与总体是数理统计中的重要概念。
样本是从总体中抽取出来的一部分个体或观察值,而总体是我们想要研究的对象的全体。
通过对样本的研究和分析,我们可以推断出总体的特征和规律。
二、数据的描述统计描述统计是数理统计中最基础的部分,它主要用于对数据进行整理、总结和分析。
描述统计包括测量中心趋势的指标(如均值、中位数和众数等)、测量散布程度的指标(如方差和标准差等)以及数据的分布形态(如偏态和峰态等)等。
通过描述统计,我们可以更好地了解数据的特点和分布规律。
三、概率分布概率分布是数理统计中的重要内容之一,它描述了随机变量的取值及其对应的概率。
常见的概率分布包括正态分布、二项分布、泊松分布等。
概率分布可以帮助我们对数据进行建模和推断,以及进行一些概率计算和预测。
四、假设检验假设检验是数理统计中用于验证统计推断的方法。
它基于样本数据对总体的某个特征进行推断,并假设了一个关于总体的假设。
通过计算样本数据与假设之间的差异,我们可以判断这个差异是否显著,从而得出是否拒绝该假设的结论。
假设检验在科学研究和实际应用中有着广泛的应用。
五、回归分析回归分析是数理统计中用于研究变量之间关系的方法。
它主要用于预测和解释因变量与自变量之间的关系。
回归分析可以通过建立模型来描述这种关系,并进一步进行参数估计和显著性检验。
常见的回归分析方法包括线性回归、多项式回归和逻辑回归等。
综上所述,数理统计的基本原理和方法涵盖了样本与总体、数据的描述统计、概率分布、假设检验和回归分析等内容。
了解和掌握这些基本原理和方法,对于进行科学研究和实际问题的解决都具有重要的指导和应用价值。
数理统计中的回归分析与ANOVA 在数理统计学中,回归分析与ANOVA(Analysis of Variance,方差分析)是两个重要的统计方法。
回归分析用于研究自变量与因变量之间的关系,ANOVA则用于比较两个或多个样本均值之间的差异。
本文将分别介绍这两个方法及其在数理统计学中的应用。
回归分析是一种用于探究自变量与因变量之间关系的统计方法。
它试图通过建立一个数学模型来描述自变量与因变量之间的函数关系。
可根据自变量的数量和类型的不同,分为简单回归和多元回归。
简单回归分析只包含一个自变量,多元回归则包含两个或两个以上的自变量。
简单回归分析的数学模型可以表示为:Y = β0 + β1X + ε,其中Y为因变量,X为自变量,β0和β1为回归系数,ε为误差。
通过最小二乘法估计回归系数,可以得到拟合的直线方程。
此外,还可以计算回归系数的显著性,利用相关系数判断回归模型的拟合程度。
多元回归分析的模型为:Y = β0 + β1X1 + β2X2 + ... + βkXk+ ε。
与简单回归相比,多元回归包含了多个自变量,可以更全面地考虑自变量对因变量的影响。
同样,可以通过最小二乘法估计回归系数,并进行显著性检验和模型拟合度评估。
回归分析在实际应用中有很多用途。
例如,可以利用回归分析预测未来销售额、研究疾病发病率与环境因素的关系、评估股市指数与经济数据的相关性等。
回归分析提供了一种量化的方法,可以揭示自变量与因变量之间的关系,从而进行决策和预测。
ANOVA是一种用于比较两个或多个样本均值之间差异的方法。
它将总体方差分解为组内方差和组间方差,并通过比较组间方差与组内方差的大小来判断样本均值是否存在显著差异。
在ANOVA中,组间方差与组内方差的比值称为F值,可以进行假设检验。
在单因素ANOVA中,只有一个自变量(因素),例如,考察不同教育水平对收入的影响。
多因素或双因素ANOVA则考虑两个或多个自变量对因变量的影响,例如,同时考察教育水平和工作经验对收入的影响。
回归的原理和步骤回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。
这种技术通常用于预测分析、时间序列模型以及发现变量之间的因果关系。
回归分析的原理基于数理统计方法,在掌握大量观察数据的基础上,建立因变量与自变量之间的回归关系函数表达式(简称为回归方程式)。
回归分析的好处良多,它可以表明自变量和因变量之间的显著关系,还可以表明多个自变量对一个因变量的影响强度。
具体步骤如下:1. 确定自变量和因变量:首先需要确定研究的目标变量作为因变量,以及可能影响该变量的各种因素作为自变量。
2. 数据收集:根据确定的自变量和因变量,收集相关数据。
数据应该是准确的、全面的,并且具有一定的代表性。
3. 数据清洗和整理:对收集到的数据进行清洗和整理,去除异常值、缺失值等,并进行必要的转换和处理。
4. 确定回归模型:根据自变量和因变量的特点以及数据的情况,选择合适的回归模型。
线性回归、多项式回归、逻辑回归等都是常用的回归模型。
5. 模型拟合:使用选定的回归模型对数据进行拟合,即根据输入的数据写出目标值的公式,这个公式可以较好地对输入的数据进行拟合。
这个公式叫做回归方程,而公式中的涉及到的系数成为回归系数。
6. 模型评估和优化:对拟合后的模型进行评估和优化,评估模型的准确性和预测能力,并根据评估结果对模型进行调整和改进。
7. 模型应用:将优化后的模型应用到实际预测中,为决策提供支持和参考。
总之,回归分析是一种强大的预测工具,可以帮助我们了解自变量和因变量之间的关系,并对未来的趋势进行预测。
在应用回归分析时,需要遵循一定的步骤和原则,确保模型的准确性和有效性。
初中数学如何进行数据的回归分析
在初中数学中,进行数据的回归分析通常是通过简单线性回归来进行的。
简单线性回归通常包括以下几个步骤:
1. 收集数据:首先,需要收集一组相关数据,通常是两组数据,一组作为自变量(x),另一组作为因变量(y)。
2. 绘制散点图:将收集到的数据绘制成散点图,以观察数据的分布情况和可能的线性关系。
3. 计算相关系数:计算自变量和因变量之间的相关系数,来衡量两组数据之间的线性关系强弱。
4. 拟合直线:利用最小二乘法,拟合一条直线来表示两组数据之间的线性关系,这条直线称为回归线。
5. 预测数值:利用回归线,可以进行数值的预测,例如根据一个自变量的数值,预测对应的因变量的数值。
这些是初中数学中常见的进行数据回归分析的步骤,希望能帮助你更好地理解。
如果有任何问题,请随时提出。
线性回归分析随着社会的发展,经济体制的改革,经济管理人员迫切需要了解到投资项目或者是工程项目的影响因素,这些对投资项目具有直接或间接的影响,通过各种各样的经济分析和技术分析方法来进行综合评价。
为了使我国在日趋激烈的竞争中立于不败之地,必须注重微观管理的决策水平,强化管理手段,而其中最有效的手段之一就是运用线性回归分析方法来确定最优方案。
线性回归分析就是根据两个或多个随机变量X、 Y的相关关系,将X的值代入一个参数方程,求出解,再利用参数的数值判断该方程能否描述这两个变量之间的关系。
线性回归分析的主要作用在于:第一,判断两个随机变量是否线性相关;第二,确定参数;第三,检验假设。
一、线性回归分析方法的介绍回归分析是数理统计的基础,它可以确定被试某种因素和某些指标之间的函数关系,也可以确定一组指标与另一组指标之间的函数关系。
一般我们常用的是线性回归分析。
线性回归分析,也称为“回归”,是数学统计学的一个基本概念。
所谓线性回归,就是依照“自变量”与“因变量”的关系,运用数学公式,将自变量的变化,导致因变量的变化,用回归方程描绘出来。
回归分析是一门应用性很强的学科,在解决实际问题时,既可以从数学上证明或计算出有关结果,又可以直接利用回归分析的结果加以利用,从而弥补了试验设计的不足。
1、解释变量变量就是要研究的因变量,通过解释变量来解释自变量的变化。
2、自变量自变量就是我们要研究的原因变量,即导致投资项目X变化的原因。
3、回归直线通过回归直线将自变量Y与因变量X之间的相互关系表现出来,反映自变量变化情况,并说明因变量X的变化对自变量Y的影响。
4、相关系数相关系数是一种表示自变量与因变量之间关系密切程度的统计量。
在同一时期内,各因素间的相关程度,相关大小的程度用r来表示。
5、 R统计量R统计量是研究对比某两种现象之间的数量关系的统计量。
2、自变量就是我们要研究的原因变量,即导致投资项目X变化的原因。
3、回归直线通过回归直线将自变量Y与因变量X之间的相互关系表现出来,反映自变量变化情况,并说明因变量X的变化对自变量Y的影响。