扬州大学材料力学试题(A)答案
- 格式:doc
- 大小:251.87 KB
- 文档页数:7

扬州大学建筑科学与工程学院材料力学 课程试卷(A )2012 ╱ 2013 学年 第1学期一. 选择题(每题3分,共18分)1、铸铁压缩试验破坏由什么应力造成?破坏断面在什么方向?以下结论哪一个是正确的? A )切应力造成,破坏断面与轴线大致成45º方向,正确答案是( ) B)切应力造成,破坏断面在横截面; C )正应力造成,破坏断面在横截面;D )正应力造成,破坏断面与轴线大致夹角成45º方向。
2、工程上通常以伸长率区分材料,对于脆性材料有四种结论,正确的是( ) A ); 5% <δ (B ); 0.5% <δ (C ); 2% <δ (D )。
% 0.2 <δ3、图示矩形,对x 、y 轴的静矩为x S 、y S ,对x ',y '轴的静矩为'x S 、'y S ,两对 静矩之间的正确关系有四种答案,其中正确的是( ) (A)x S ='x S ,y S ='y S ; (B)x S =-'x S ,y S =-'y S ; (C)x S =-'x S ,y S ='y S ; (D)x S ='x S ,y S =-'y S 。
4、正方形等截面立柱,受纵向压力F 作用。
当力F 作用点由A 移至B 时,柱内最大压应力的比值maxmaxB A σσ有四种答案,其中正确的是( )(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。
5、空心圆轴受扭转力偶作用,横截面上的扭矩为T ,下列四种(横截面上)沿径向的应力分布图中正确的是( )。
(A)(B) (C) (D) 6、图示单元体所示的应力状态按第四强度理论,其相当应力4r σ为( )。
(A ).2/3σ; (B ).2/σ; (C ).2/7σ; (D ).2/5σ。
σ=/2二.填空题(每空2分,共10分)1、销钉接头如图所示。

材料力学A期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,以下哪项不是应力的分类?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C2. 在拉伸试验中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料弹性极限的应力D. 材料达到最大应力的点答案:A3. 根据胡克定律,当材料受到拉伸时,其应力与应变的关系是:A. 线性关系B. 非线性关系C. 无关系D. 指数关系答案:A4. 梁的弯曲应力公式中,应力与下列哪项无关?A. 弯矩B. 截面惯性矩C. 材料的弹性模量D. 梁的长度答案:D5. 以下哪种材料不属于各向同性材料?A. 木材B. 钢材C. 玻璃D. 碳纤维复合材料答案:D6. 材料力学中,泊松比是描述材料在受到轴向拉伸时:A. 横向应变与轴向应变的比值B. 轴向应变与横向应变的比值C. 剪切应变与轴向应变的比值D. 剪切应变与横向应变的比值答案:A7. 材料的疲劳破坏通常发生在:A. 最高应力点B. 最低应力点C. 应力集中区域D. 材料的中心答案:C8. 梁在纯弯曲时,其横截面上的正应力分布规律是:A. 线性分布B. 抛物线分布C. 指数分布D. 对数分布答案:B9. 材料力学中,剪切模量与弹性模量的关系是:A. 互为倒数B. 互为平方根C. 互为常数倍D. 互为对数关系答案:C10. 材料力学中,以下哪项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度答案:D二、简答题(每题10分,共40分)1. 简述材料力学中的三种基本变形类型。
答案:材料力学中的三种基本变形类型包括拉伸和压缩、剪切和扭转、弯曲。
2. 描述材料的弹性模量和剪切模量的定义及其物理意义。
答案:弹性模量(E)定义为材料在弹性范围内应力与应变的比值,反映了材料抵抗轴向变形的能力。
剪切模量(G)定义为材料在剪切应力作用下剪切应力与剪切应变的比值,反映了材料抵抗剪切变形的能力。

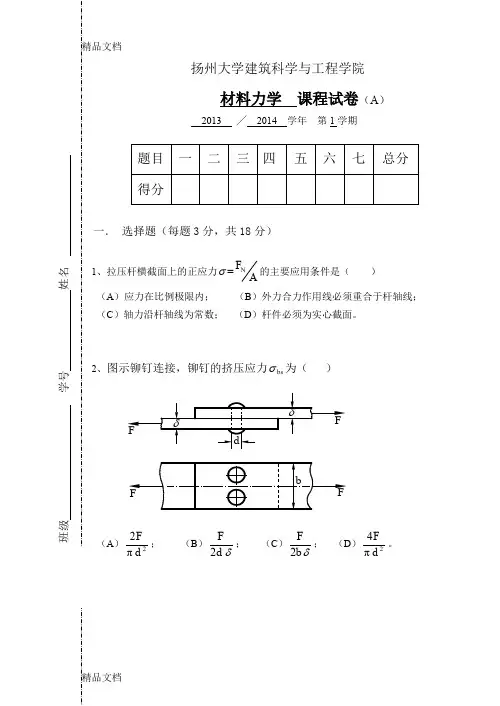
扬州大学建筑科学与工程学院材料力学 课程试卷(A )2013 ╱ 2014 学年 第1学期题目 一 二 三 四 五 六 七 总分 得分一. 选择题(每题3分,共18分)1、拉压杆横截面上的正应力NF =A σ的主要应用条件是( )(A )应力在比例极限内; (B )外力合力作用线必须重合于杆轴线; (C )轴力沿杆轴线为常数; (D )杆件必须为实心截面。
2、图示铆钉连接,铆钉的挤压应力bs σ为( )(A )2 π2d F ; (B )δ 2d F ; (C )δ 2b F ; (D )2π4d F。
班级 学号 姓名FFδδFFbd3、由惯性矩的平行移轴公式,2z I 等于( )(A )4/312bh I I z z +=; (B )4/32bh I I z z +=; (C )32bh I I z z +=; (D )312bh I I z z +=。
4、正方形等截面立柱,受纵向压力F 作用。
当力F 作用点由A 移至B 时,柱内最大压应力的比值A max B max σσ有四种答案,其中正确的是( )(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。
x yF F B A Oaaz5、内径为d ,外径为D 的四根空心圆轴,两端均承受相同的扭转力偶作用。
设四根轴的内外径之比D d =α分别为0,0.5,0.6和0.8,但横截面面积都相等,其承载能力最大yzz 1z 2h /2h /2h /2b /2b /2的轴( )(A) 0=α; (B) 5.0=α; (C) 6.0=α; (D) 8.0=α6、梁的弯曲刚度EI 为常数,今欲使梁的挠曲线在x=l/3处出现一拐点,则比值Me1/Me2为( )(A) M e1/M e2=2; (B)M e1/M e2=3; (C)M e1/M e2=1/2; (D)M e1/M e2=1/3。
二.填空题(每空2分,共10分)1、图示单元体所示的应力状态按第四强度理论,其相当应力r3σ为 。


XX学院2014-2015学年第二学期期末考试A卷参考答案及评分标准试卷编号:课程名称:材料力学课程归属:土木工程系适用专业(班级):土木工程出卷人:学科部主任:一、填空题(每空1分,共10分)1.剪切弯曲2.弹性阶段强化阶段3.04.变截面梁5.弯曲变形6.27.[一、2)2 + 02 - $3)2 + ($3 - $1 广 I 8.F二、单项选择题(每小题2分,共20分)9-13 ABDDC 14-18 BDBBD三、简述题(共14分)19.答:线弹性和小变形(4分)。
叠加在本质上是几何和,如不同方向的位移、正应力和切应力、正应变和切应变间的叠加(2分);但同一方向的多个位移、同一方向的多个正应变、正应力、切应力在规定了其符号后,叠加是代数求和(2分)。
20.答:1)、减小梁的跨度,增加支承约束;(2分)2)、调整加载方式,改善结构设计;(2 分)3)、增大截面惯性矩,改变截面形状。
(2分)四、作图题(共15分)21.略22.略五、计算题(共41分)23.(1)弹性模量E是表征材料抵抗弹性变形的能力;(2分)(2)E(./E s;(2 分)(3)E s/E c : (2 分)(4)=3\.5MPa(2 分):= 4.2MPa(2 分)•J c24.(1)c Ali = 5MPa(2 分)(7liC = 20MPa(2 分)(y(D = 7.5MPci(2 分)(2)A/.w = -0.03Smm(3 分),225.(1)M心= J = "l.25KN m(1 分)iTldX 8hh2W、=——= 648xlQ-6m3(1 分)cr inax=也些=1 JAMPa > [b] = 1 OMPa(2 分)max ▼ j r- 」此梁强度不够(1分)(2)[q] = 2.07 KN/m(3 分)(3)h = 2\(2 分)b - 144mm(2 分)26.计算挺杆柔度九=J宇=92.9 (2 分)人=« = 128.5 (2 分).I4>九,可见挺杆为大柔度压杆(2分)可以用欧拉公式FI= —— = 6.3xlO37V (2 分)Frr3VF 〃=工=3.58>〃“,安全。
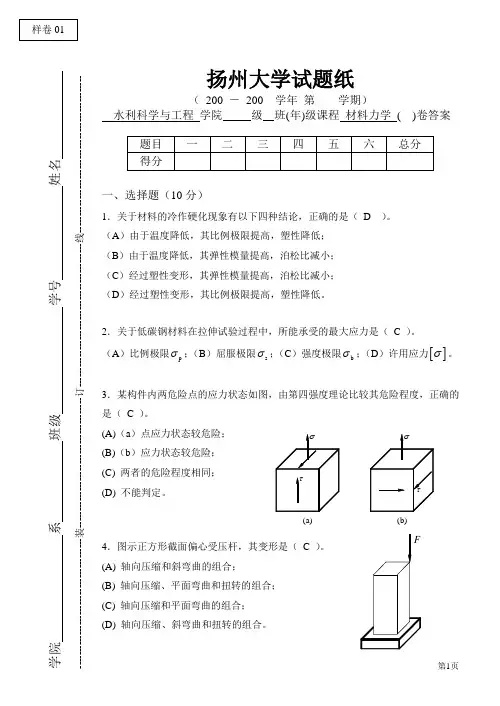
第1页扬州大学试题纸( 200 - 200 学年 第 学期)水利科学与工程 学院 级 班(年)级课程 材料力学 ( )卷答案一、选择题(10分)1.关于材料的冷作硬化现象有以下四种结论,正确的是( D )。
(A )由于温度降低,其比例极限提高,塑性降低; (B )由于温度降低,其弹性模量提高,泊松比减小; (C )经过塑性变形,其弹性模量提高,泊松比减小; (D )经过塑性变形,其比例极限提高,塑性降低。
2.关于低碳钢材料在拉伸试验过程中,所能承受的最大应力是( C )。
(A )比例极限p σ;(B )屈服极限s σ;(C )强度极限b σ;(D )许用应力[]σ。
3.某构件内两危险点的应力状态如图,由第四强度理论比较其危险程度,正确的是( C )。
(A)(a )点应力状态较危险; (B)(b )应力状态较危险; (C) 两者的危险程度相同; (D) 不能判定。
4.图示正方形截面偏心受压杆,其变形是( C )。
(A) 轴向压缩和斜弯曲的组合; (B) 轴向压缩、平面弯曲和扭转的组合; (C) 轴向压缩和平面弯曲的组合; (D) 轴向压缩、斜弯曲和扭转的组合。
(a)(b)5.图示截面为带圆孔的方形,其截面核心图形是(B )。
二、填空题(20分)1.一受扭圆轴,横截面上的最大切应力max40MPaτ=,则横截面上点A的切应力Aτ=__MPa3.33__。
2.悬臂梁受力如图示,当梁直径减少一倍,则最大挠度w max是原梁的__16___倍,当梁长增加一倍,而其他不变,则最大转角θmax是原梁的__4____倍。
3.铆接头的连接板厚度为δ,铆钉直径为d。
则铆钉切应力τ=__22Fdπ___,最大挤压应力bsσ=__Fdδ___。
(mm)(A) (B) (C) (D)第2页第3页4.由同一种材料组成的变截面杆的横截面面积分别为2A 和A ,受力如图示,弹性模量为E 。
截面D 水平位移为___EAFl2___。
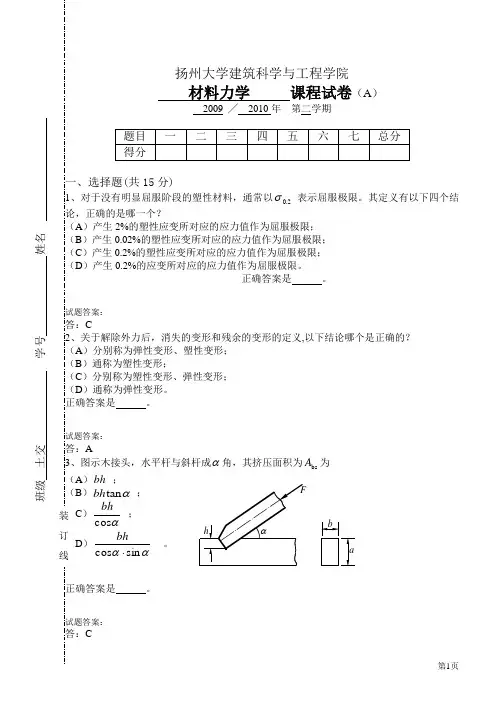
扬州大学建筑科学与工程学院材料力学 课程试卷(A )2009 ╱ 2010年 第二学期题目 一 二 三 四 五 六 七 总分 得分一、选择题(共15分)1、对于没有明显屈服阶段的塑性材料,通常以 2.0σ表示屈服极限。
其定义有以下四个结论,正确的是哪一个?(A )产生2%的塑性应变所对应的应力值作为屈服极限; (B )产生0.02%的塑性应变所对应的应力值作为屈服极限; (C )产生0.2%的塑性应变所对应的应力值作为屈服极限; (D )产生0.2%的应变所对应的应力值作为屈服极限。
正确答案是 。
试题答案:答:C2、关于解除外力后,消失的变形和残余的变形的定义,以下结论哪个是正确的? (A )分别称为弹性变形、塑性变形; (B )通称为塑性变形;(C )分别称为塑性变形、弹性变形; (D )通称为弹性变形。
正确答案是 。
试题答案:答:A3、图示木接头,水平杆与斜杆成α角,其挤压面积为bs A 为 (A )bh ;(B )αtan bh ;(C )α cos bh; (D )αα sin cos ⋅bh 。
正确答案是 。
试题答案:答:CFhαba装 订线班级 土交 学号 姓名4、由惯性矩的平行移轴公式,2z I 的答案有四种: (A)4/312bh I I z z +=; (B)4/32bh I I z z +=; (C)32bh I I z z +=; (D)312bh I I z z +=。
答:C5、铁构件受力如图所示,其危险点的位置有四种答案:(A) A 点; (B) B 点; (C) C 点; (D) D 点。
A DCB F 1F 3F 2答:(D)二、填空题(共20分)1、木材的 纹拉伸强度高, 纹拉伸强度低。
答:顺、横。
2、弹性模量GPa 200=E 的试件,其应力-应变曲线如图示,A 点为屈服极限MPa 240s =σ。
当拉伸至B 点时,在试样的标距中测得纵向线应变为3103-⨯,试求从B 点卸载到应力为140 MPa 时,标距内的纵向线应变ε。

班号 学号 姓名 成绩《 材 料 力 学 A 》期末试卷一、选择题 (单选,共12分,每小题3分) 1、下列说法正确的是: 。
A 、各向同性材料是指材料内部任意位置的力学性能都是相同的;B 、材料的刚度越大越不容易发生屈服变形;C 、塑性材料的强度极限高于脆性材料的强度极限;D 、脆性材料的单向压缩许用应力一般高于单向拉伸许用应力。
2、下列说法正确的是 。
A 、薄壁圆管的扭转切应力公式只适用于线弹性、各向同性材料;B 、任意截面形状的闭口薄壁杆横截面上的扭转切应力为常数;C 、开口薄壁杆的抗扭性能很差,对于受扭构件,一般不要采用开口薄壁杆;D 、圆轴扭转的刚度条件是圆轴的抗扭模量不能超过许用值。
3、下图所示两均质矩形截面等厚梁,两梁材料相同、总长度相同、AB 段完全相同、BC 段的梁高度不同。
下面结论中正确的是: 。
A 、两梁B 截面的挠度和转角相同; B 、两梁B 截面的挠度和转角不相同;C 、两梁C 截面的挠度和转角相同;D 、图(a )所示梁C 截面挠度和转角均小于图 (b )所示梁C 截面的挠度和转角。
F图(b )4、下图所示正方形截面杆件,横截面ABCD 上拉应力最大的点是 。
二、填空题(8分,每空1分)1、由于截面急剧变化引起的应力局部增大现象,称为 。
2、 称为叠加原理。
当构件的受力和变形满足 条件与 条件时, 叠加原理方能适用。
3、在进行纯弯梁横截面上正应力分析时,除了运用静力学方程外,还运用了 方程与 方程,并根据梁的变形特点作 假设与 假设。
F三、计算题(5道小题,共80分)1、某等截面实心传动轴,转速n =300r/min ,轮1为主动轮,输入功率P 1=50kW ,轮2、轮3与轮4为从动轮,输出功率分别为P 2=10kW ,P 3= P 4=20kW 。
(力矩与功率、转速之间的转换关系为:{}{}{}/min9549kWN m r P M n ⋅=)1)试画轴的扭矩图;2) 若许用切应力[τ]=80MPa ,单位长度的许用扭转角[θ]=0.8(˚)/m ,切变模量G =80GPa ,试确定轴径d 。
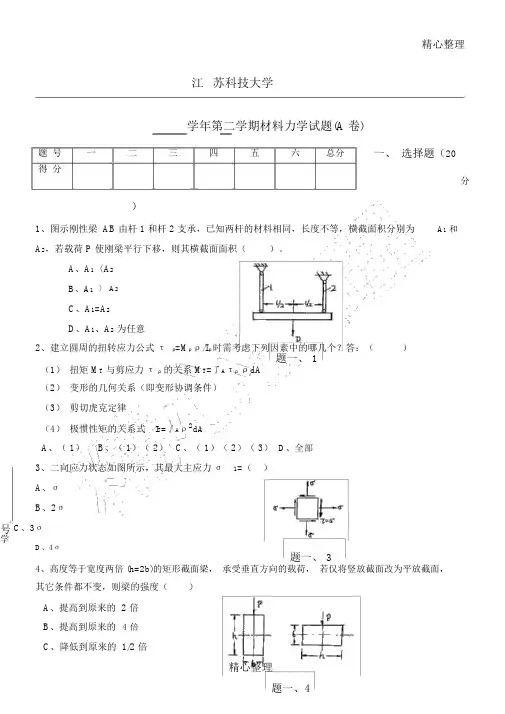
精心整理江苏科技大学学年第二学期材料力学试题(A 卷)题号一二三四五六总分一、选择题(20 得分分)A1和1、图示刚性梁 AB 由杆 1 和杆 2 支承,已知两杆的材料相同,长度不等,横截面积分别为A2,若载荷 P 使刚梁平行下移,则其横截面面积()。
A、A1〈A2B、A1 〉 A2C、A1=A2D、A1、A2为任意2、建立圆周的扭转应力公式τρ=Mρ ρ/Iρ 时需考虑下列因素中的哪几个?答:()题一、 1(1)扭矩 M T与剪应力τρ的关系 M T=∫AτρρdA(2)变形的几何关系(即变形协调条件)(3)剪切虎克定律(4)极惯性矩的关系式I T=∫Aρ2dAA、( 1)B、( 1)( 2)C、( 1)( 2)( 3)D、全部3、二向应力状态如图所示,其最大主应力σ1=()A、σB、2σ号C、3σ学D、4σ题一、 34、高度等于宽度两倍 (h=2b)的矩形截面梁,承受垂直方向的载荷,若仅将竖放截面改为平放截面,其它条件都不变,则梁的强度()A、提高到原来的 2 倍B、提高到原来的 4 倍C、降低到原来的 1/2 倍D、降低到原来的1/4 倍5.已知图示二梁的抗弯截面刚度EI 相同,若二者自由端的挠度相等,则 P1/P2=()A、2题一、 5B、4C、8D、16二、作图示梁的剪力图、弯矩图。
(15分)二题三、如图所示直径为 d 的圆截面轴,其两端承受扭转力偶矩 m 的作用。
设由实验测的轴表面上与轴线成 450方向的正应变,试求力偶矩 m 之值、材料的弹性常数 E、μ均为已知。
(15 分)四、电动机功率为 9kW,转速为 715r/min ,皮带轮直径 D=250mm,主轴外伸部分长度为l=120mm,主轴直径 d=40mm,〔σ〕 =60MPa,用第三强度理论校核轴的强度。
( 15 分)三题五、重量为 Q 的重物自由下落四在题图图示刚架 C 点,设刚架的抗弯刚度为 EI,试求冲击时刚架D 处的垂直位移。
扬州大学建筑科学与工程学院材料力学 课程试卷(A )2009 ╱ 2010年 第二学期题目 一 二 三 四 五 六 七 总分 得分一、选择题(共15分)1、对于没有明显屈服阶段的塑性材料,通常以 2.0σ表示屈服极限。
其定义有以下四个结论,正确的是哪一个?(A )产生2%的塑性应变所对应的应力值作为屈服极限; (B )产生0.02%的塑性应变所对应的应力值作为屈服极限; (C )产生0.2%的塑性应变所对应的应力值作为屈服极限; (D )产生0.2%的应变所对应的应力值作为屈服极限。
正确答案是 。
试题答案:答:C2、关于解除外力后,消失的变形和残余的变形的定义,以下结论哪个是正确的? (A )分别称为弹性变形、塑性变形; (B )通称为塑性变形;(C )分别称为塑性变形、弹性变形; (D )通称为弹性变形。
正确答案是 。
试题答案:答:A3、图示木接头,水平杆与斜杆成α角,其挤压面积为bs A 为 (A )bh ;(B )αtan bh ;(C )α cos bh; (D )αα sin cos ⋅bh 。
正确答案是 。
试题答案:答:CFhαba装 订线班级 土交 学号 姓名4、由惯性矩的平行移轴公式,2z I 的答案有四种: (A)4/312bh I I z z +=; (B)4/32bh I I z z +=; (C)32bh I I z z +=; (D)312bh I I z z +=。
答:C5、铁构件受力如图所示,其危险点的位置有四种答案:(A) A 点; (B) B 点; (C) C 点; (D) D 点。
A DCB F 1F 3F 2答:(D)二、填空题(共20分)1、木材的 纹拉伸强度高, 纹拉伸强度低。
答:顺、横。
2、弹性模量GPa 200=E 的试件,其应力-应变曲线如图示,A 点为屈服极限MPa 240s =σ。
当拉伸至B 点时,在试样的标距中测得纵向线应变为3103-⨯,试求从B 点卸载到应力为140 MPa 时,标距内的纵向线应变ε。
扬州大学建筑科学与工程学院材料力学、结构力学 课程试卷材料力学一.选择题(每题3分,共18分)1.关于低碳钢材料在拉伸试验过程中,所能承受的最大应力是 。
(A )比例极限p σ;(B )屈服极限s σ;(C )强度极限b σ;(D )许用应力 ][σ。
2.插销穿过水平放置的平板上的圆孔,在其下端受有一拉力P .该插销的剪切面面积和挤压面积分别等于 。
(A) πdh ,πD 2/4; (B) πdh ,π(D 2-d 2)/4; (C) πDh ,πD 2/4; (D) πDh ,π(D 2-d 2)/4。
第2题图 第3题图 3.左端固定的直杆受扭转力偶作用,如图所示。
在截面1-1和2-2处扭矩为 。
(A) M 1-1=12.5kNm,M 2-2= -3kNm 。
(B) M 1-1= -2.5kNm, M 2-2= -3kNm 。
(C) M = -2.5kNm,M =3kNm 。
(D) M =2.5kNm, M = -3kNm 。
24.T 形截面梁,两端受力偶矩M 0作用,如图示。
若材料的抗压许用应力[σy ]大于抗拉许用应力[σl ],则梁截面的正确位置是 。
5.图示正方形截面偏心受压杆,其变形是 。
(A)轴向压缩和斜弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)轴向压缩和平面弯曲的组合;(D)轴向压缩、斜弯曲和扭转的组合。
第5题图 第6题图6.图示单元体应力状态为___ ___。
(A) 单向应力状态 (B) 二向应力状态 (C) 三向应力状态 (D) 无法确定 二.填空题(每空2分,共24分) 1.一受扭圆轴,横截面上的最大切应力MPa 40max =τ,则横截面上点A 的切应力=A τ 。
2.悬臂梁受力如图示,当梁直径减少一倍,则最大挠度wmax 是原梁的 倍,当梁长增加一倍,而其他不变,则最大转角θmax 是原梁的 倍。
(mm)第1题图 第2题M M 0DC3.低碳钢在拉伸时一般要经历_______________、_______________、_______________、和_______________四个阶段。
材料力学试卷含答案《材料力学》考试试卷(a卷)班名和学号题号得分一二三四五六七总得分评卷人审核人一、选择题(每题4分,共16分)1.图中所示的直杆为3A长,材料的拉伸刚度为ea,应力如图所示。
杆中点处横截面的垂直位移为。
(a)0;(b)pa/(ea);(c)2pa/(ea);(d)3pa/(ea)。
2.如果由相同材料制成的空心圆轴和实心圆轴具有相同的长度和横截面积,则扭转刚度较大的轴为空。
(a)实心圆轴;(b)空心圆轴;(c)二者一样;(d)无法判断。
3.图示铆钉联接,铆钉的挤压应力?bs是。
(a) 2p/(d);(b)p/(2dt);(c)p/2bt;(d)4p/(d)22第1页,共7页4.关于图示梁上a点的应力状态为。
二、填空(每个问题4分,共12分)1.图示三种截面的截面积相等,高度相同,试按其抗弯截面模量由大到小依次排列,wz()?wz()?wz()2.已知一点的应力状态如图,其相当应力?r4=mpa3.已知图(a)所示梁中点C的挠度为YC?PB3l2?4b2?/(48ei),(a?b)。
如图(b)所示梁中点c的挠度为yc=。
第2页,共7页三、作图题(本题12分):梁图Q和m四、计算题(本题15分)延伸梁的截面和荷载如图所示,称为i104z?500? 四次方,材料的[?t]?15mpa,[?c]?40mpa,核该梁的强度。
第3页,共7页校五、计算题(15分)图示结构,横梁横截面为10号工字钢。
wz=49cm,bd直杆横截面为矩形20×30mm,两端为球铰,材料的弹性模量e=200gpa,?p=100,稳定安全系数nst=2.5,横梁许用应力[?]=140mpa,试校核结构是否安全。
三六、计算题(20分)本图为精密磨床砂轴示意图。
已知电机功率P=3KW,转子转速n=1400R/min,转子重量W1=101n。
砂轮直径d=250mm,砂轮重量W2=275n。
磨削力FY:FZ=3:1,砂轮轴直径d=50mm,材料处于应力状态,计算主应力和最大剪应力。
扬州大学建筑科学与工程学院
材料力学 课程试卷(A )
2009 ╱ 2010年 第二学期
题目 一 二 三 四 五 六 七 总分 得分
一、选择题(共15分)
1、对于没有明显屈服阶段的塑性材料,通常以 2.0σ表示屈服极限。
其定义有以下四个结论,正确的是哪一个?
(A )产生2%的塑性应变所对应的应力值作为屈服极限; (B )产生0.02%的塑性应变所对应的应力值作为屈服极限; (C )产生0.2%的塑性应变所对应的应力值作为屈服极限; (D )产生0.2%的应变所对应的应力值作为屈服极限。
正确答案是 。
试题答案:
答:C
2、关于解除外力后,消失的变形和残余的变形的定义,以下结论哪个是正确的? (A )分别称为弹性变形、塑性变形; (B )通称为塑性变形;
(C )分别称为塑性变形、弹性变形; (D )通称为弹性变形。
正确答案是 。
试题答案:
答:A
3、图示木接头,水平杆与斜杆成α角,其挤压面积为bs A 为 (A )bh ;
(B )αtan bh ;
(C )α cos bh
; (D )αα sin cos ⋅bh 。
正确答案是 。
试题答案:
答:C
F
h
α
b
a
装 订
线
班级 土交 学号 姓名
4、由惯性矩的平行移轴公式,2z I 的答案有四种: (A)4/3
12bh I I z z +=; (B)4/3
2bh I I z z +=; (C)32bh I I z z +=; (D)312bh I I z z +=。
答:C
5、铁构件受力如图所示,其危险点的位置有四种答案:
(A) A 点; (B) B 点; (C) C 点; (D) D 点。
A D
C
B F 1
F 3
F 2
答:(D)
二、填空题(共20分)
1、木材的 纹拉伸强度高, 纹拉伸强度低。
答:顺、横。
2、弹性模量GPa 200=E 的试件,其应力-应变曲线如图示,A 点为屈服极限MPa 240s =σ。
当拉伸至B 点时,在试样的标距中测得纵向线应变为3103-⨯,试求从B 点卸载到应力为140 MPa 时,标距内的纵向线应变ε。
/MPa σ-3
10/⨯εO 3140240
A B y
z
z 1
z 2
h /2
h /2
h /2
b /2
b /2
解:B 点应变包括两部分:)()(P e 塑性和弹性εε 所以 p e 3103εε+=⨯-
3
e 102.1-⨯==
E
σ
ε
得 3p 108.1-⨯=ε
又从B 点卸载到C 点时
3'e 107.0-⨯==E
σ
ε
则 3p 'e 105.2-⨯=+=εεε
3、销钉接头如图所示。
销钉的剪切面面积为 ,挤压面面积为 。
答:剪切面面积为bh 2;挤压面面积为bd 。
4、试根据载荷及支座情况,写出由积分法求解时,积分常数的数目及确定积分常数的条件。
积分常数 个,
边界条件与连续条是 。
w F
x B
A
2l
l
l C D
答: 6,x =0,w 1=0,1
w '=0;x =2l ,w 1=w 2;x =3l ,w 2=0,w 3=0,32w w '='。
/MPa
σ-3
10/⨯εO 3
140
240A
B
O 1
d h F b
F C
A
B
l
b
h 5、已知图(a )图(b )简直梁EI a /EI b =1:2试求两梁跨中挠度之比w a / w b =__________。
6、拉+弯+扭组合变形杆内危险点处的应力:A F N F N
=
σ,W M M =σ,p
x M W M x =τ;按第三强度理论建立的强度条件为=*
3
σ_____________][σ≤。
三、计算题(共65分)
1、图示木梁受一移动载荷F 作用。
已知20 kN F =,梁材料的
[]10 MPa, [] 3 MPa στ==, 1 m l =,横截面高宽比3
2
h b =,试确定截面尺寸。
解:当F 走到跨中央时,
max max max 39, [], 165 mm 44M Fl Fl
M h W h
σσ=
==≤≥ 当F 离支座很近时,Smax F F =
Smax max 239[], 122 mm 24F F
h A h
ττ==≤≥
取 165 mm h =, 则 2110 mm 3h
b ==
L
L
2F
L /2 L /2
F
2.示圆截面悬臂梁所受载荷F 1 = F 2 = F ,力偶矩M e = Fa ,其中a 为A-A 截面距右端的距离,圆截面的直径为D ,材料的弹性模量为E ,泊松比为μ。
1)在图中画出A-A 截面上,拉应力最大的点的位置。
2)计算梁A-A 截面上,该点的主应力和最大拉应变的值。
解:
该点的位置如图
3232D Fa πσ=
, 3
16D Fa
πτ= )32(16)2(23
223
,1±=+±=D Fa πτσσσ
02=σ
3
3223
1131612161)2(121D Fa
E D Fa E E E E
πμπμτσμσμμσσε++-=+++-=
-=
τ
σ
y
z 45︒
C
O
A
a
A D
x y
z F 2
F 1
M e y
z
A-A 截面
3.构件内某点周围取出一边长为a 的正方形单元体如图所示,根据理论计算已经求得σ =50 MPa ,,τ =50MPa ,材料弹性模量E = 200GPa , 泊松比 μ = 0.3。
试求:对角线AC 的长度改变量。
解MPa 10045=︒-σ, 045=︒σ
6454510500-︒
-︒-⨯==
=E
AC σεε
6102500-⨯=⋅=∆a l l AC AC AC ε
τ
A
C
σ
σ
τ
σ
σ
4、图示结构为正方形,由5根圆杆组成,各杆直径均为40 mm d =, 1 m a =,材料均为低碳钢,弹性模量210 GPa E =,屈服极限s 240 MPa σ=,比例极限p 210 MPa σ=,直线经验公式为cr (304 1.12) MPa σλ=-,稳定安全因数st [] 1.89n =,材料的许用应力
[]160 MPa σ=,试求结构的许可载荷[]F 。
解:1. 由平衡方程可知,杆AB ,AD ,BC ,CD 为拉杆, 且N N N N N 2
2cos 452
AB AD BC CD F F F F F F F ======
杆BD 为压杆,N BD F F = 2. 由拉杆强度条件
N
[]F A
σσ=
≤ 得 2[
]284.4 k N F A σ≤= 3. 由压杆稳定计算
p 141.499.9λλ=>=
由欧拉公式:cr 130.3 kN F =
cr
st N []BD
F n F ≥ cr st
68.9 kN []F
F n ≤=
结构许可载荷[]68.9 kN F =。
B A
a a F F
C D。