圆柱的体积1

求圆柱体积的公式圆柱体积的公式是通过确定其半径和高度来计算的，通常表示为V。

圆柱体积公式：V=π*r^2*h圆柱体积的推导：首先，我们要了解圆柱体的基本形状和特征。

圆柱体由两个平行的圆底面以及这两个底面之间的侧面组成。

我们可以将其想象为由许多带有相同半径的圆叠加而成。

我们希望找到一个公式来计算圆柱体的体积。

想象一下，我们可以将圆柱体切割成无数薄片，每一片都是一个圆盘。

如果我们能够计算出一个圆盘的体积，然后将所有的圆盘的体积相加，那么最终得到的就是圆柱体的体积。

接下来我们来计算一个圆盘的体积。

圆盘的体积可以看作是一个薄圆柱体的体积，其高度为圆盘的厚度。

薄圆柱体的体积公式为V=π*r^2*h，其中，r为薄圆柱体的底面半径，h为薄圆柱体的高度。

如果我们将圆柱体切割成无数个这样的薄圆柱体，每个薄圆柱体的厚度都非常小，那么我们可以将每个薄圆柱体的体积相加，得到整个圆柱体的体积。

现在让我们思考一下，当我们把无限个薄圆柱体的体积相加时，会有什么结果？由于每个薄圆柱体的体积等于π*r^2*h，而每个薄圆柱体的高度h非常小，所以可以近似认为每个薄圆柱体的体积都非常接近于0。

所以，当我们将无数个薄圆柱体的体积相加时，由于每个薄圆柱体的体积都非常接近于0，所以相加的结果也会接近于实际的圆柱体体积。

因此，我们可以认为圆柱体的体积可以用薄圆柱体的体积来近似表示。

最后，我们得到了计算圆柱体体积的公式：V=π*r^2*h。

这个公式通过底面半径r和高度h来计算圆柱体的体积。

需要注意的是，计算圆柱体的体积时，半径和高度的单位必须一致。

如果半径的单位为米，高度的单位也必须为米，否则计算出的结果将不正确。

圆柱体积公式的应用：圆柱体积的公式在日常生活和工程应用中有着广泛的应用。

例如，在建筑工程中，使用圆柱体体积公式可以计算柱体的体积，进而确定混凝土的用量。

在容器设计中，通过圆柱体体积公式可以确定容器的存储容量，帮助设计者选择合适的容器尺寸。

1米圆柱的立方计算公式
一米圆柱的立方是指一个立体形状的圆柱，其直径和高度都为1米。

立方的计算公式可以用来计算一米圆柱的体积。

一米圆柱的立方计算公式如下：
体积(V) = pi × r²h
其中，pi 为圆周率，r 为圆柱的半径，h 为圆柱的高度。

对于一米圆柱的立方而言，r 为 0.5 米，h 为 1 米，因此其体积有：
体积(V) = pi × (0.5)² × 1 = pi × 0.25
于是，一米圆柱的立方体积为 pi × 0.25 = 0.785 平方米。

这个体积大约等于一个拳头大小的立方物体，或者相当于一个水果盘的容量。

使用上面的公式，也可以改变r, h的值来计算不同大小的圆柱的体积。

但是要注意，圆柱的半径和高度都必须是可以表示成一个统一的尺度来进行计算。

否则，计算结果可能会出现圆柱体积超出预期的情况。

《圆柱的体积》教学设计《圆柱的体积》教学设计1教学圆锥的体积是在掌握了圆锥的认识和圆柱的体积的基础上教学的。

教学时让学生通过实验来发现圆锥与等底等高的圆柱之间的关系，从而得出圆锥的体积等于和它等底等高的圆柱体积的三分之一，并能运用这个关系计算圆锥的体积，让学生从感性认识上升到理性认识。

我让学生观察，先猜测圆锥的体积和什么有关，学生联系到了圆柱的体积，在猜想中激发学生的学习兴趣，使学生明白学习目标。

教师从展示实物图形到空间图形，采用对比的方法，不断加深学生对形体的认识。

然后让学生动手实验：有的组用捏橡皮泥的方法，有的组用到沙子的方法；有的组用计算的方法。

让孩子亲历教学的验证过程，从实验中得出结论：等底等高的圆锥体体积是圆柱体体积的三分之一，从而推出圆锥的体积公式。

接着我趁热打铁，让学生想一想等积等高的时候，圆柱和圆锥有什么样的关系？等积等底的时候，圆柱和圆锥又会有什么样的关系？这样，就有一种水到渠成的感觉。

对圆锥的体积建立了鲜明的印象之后，就应用公式解决实际的生活问题，起到巩固深化知识点的作用。

圆锥的体积这节课的教学具有下面的特点，一是在教学新课时，没有像传统教学那样，直接拿出等底等高的圆柱和圆锥容器的教具，让学生观察倒沙实验，而是通过师生交流、问答、猜想等形式，调动学生的积极性，激发学生强烈的探究欲望，学生迫切希望通过实验来证实自己的猜想，所以做起实验就兴趣盎然；二是在实验时，让学生小组合作亲自动手实验，以实验要求为主线，即动手操作，又动脑思考，努力探索圆锥体积的计算方法。

这样的学习，学生学的活，记得牢，即发挥教师的主导作用，又体现了学生的主体地位。

学生在学习的过程中，始终是一个探索者、研究者、发现者，并获得了富有成效的学习体验在教学之后感觉到遗憾的是，由于教具有限，参与实验的学生不多，如果每个小组准备一套学具，让他们以小组合作学习的方式使每个学生都能真切的参与到探究中去，这样每个学生都能怀着喜悦的心情进行学习，最大限度的发挥每个学生的自主学习的能力，这样的学习不仅使学生学会了知识，更重要的是培养了学生的能力。

圆柱体体积公式单位
圆柱体体积公式是V=π×r^2×h，其中r 为底面半径，h 为高，V 为体积。

单位可以根据具体情况选择，但要保持一致。

例如，如果高是米，则半径也是米，底面积是平方米；如果高是厘米，则半径也是厘米，底面积是平方厘米。

圆柱体体积公式的单位是立方单位，例如立方米、立方厘米等。

具体单位取决于所选择的长度单位。

例如，如果半径和高都是以厘米为单位，则体积的单位就是立方厘米；如果半径和高都是以米为单位，则体积的单位就是立方米。

总之，在进行圆柱体体积计算时，需要保持单位的一致性，并根据具体情况选择合适的单位。

圆柱立方的简便计算方法圆柱立方形是一种较为常见的三维形状，例如铅笔盒、饮料瓶都是圆柱立方形。

计算圆柱立方的体积和表面积是数学学科中的基础知识之一，也是日常生活中的实用技能。

下面介绍一些圆柱立方的简便计算方法。

一、计算体积1. 体积的公式为：体积 = 底面积 * 高一个圆柱体积为底面积和高的乘积，而底面积为底面圆的面积。

因此，给定圆柱的半径 r 和高 h，可按下式计算体积：V = πr²h当然，如果没有半径的具体数值，也可从圆周长推算，并代入公式中：C = 2πrr = C/2π2. 用水量估算圆柱体积如果碰到一些特殊情况，例如无法精确地测量圆柱的底面积和高，但能确定圆柱形的外形，也可以用水量来估算圆柱体积。

首先，找一个与圆柱近似大小的容器，并将它注满水。

把圆柱体往里面沉，这时水位上升的高度就等于圆柱的高度。

测量水的体积，即为圆柱的体积。

无论如何，估算的圆柱类型和容器中的水的密度都是两个不确定的因素。

但是这种方法可以给出一个近似值。

二、计算表面积1. 表面积的公式为：表面积= 2πr² + 2πrh一个圆柱的表面积是两倍于其底面圆的面积，再加上一个环形侧面的面积。

圆柱侧面的面积相当于一个矩形，它的长度等于圆周长，宽度等于圆柱的高。

需要注意的是，如果该圆柱顶部与底部都被盖住了，那么它的表面积将不包括顶部和底部的圆面积。

2. 利用逆向思维估算表面积当一些场合需要粗略地估算表面积时，可以考虑这种逆向思维的方法。

首先，将一个白纸固定在圆柱体的侧面上，然后沿着圆柱体的边缘进行裁剪，将白纸展平。

此时展平的白纸的面积就是圆柱体的侧面积，而圆柱底面积则已经定义为一个圆的面积。

算起来，圆柱的表面积等于裁剪后的白纸与一个底面圆的面积之和。

总之，圆柱立方的计算公式并不复杂，但方法却可以多样化，选择适合自己的计算方法可以提升计算效率。

圆柱体体积公式计算
圆柱体是几何几何图形中，与平面图形最为接近的三维几何图形之一。

它是由底部的圆面和沿着中轴线的高度相组合而成的，有着独特的外形和十分复杂的几何结构。

圆柱体的计算是一门数学的基础课程，其中，计算圆柱体的体积占据了十分重要的一部分。

首先，计算圆柱体的体积需要使用到公式：V =r2h (π=3.14, h=高度, r=半径)。

在这个公式中，“V”代表圆柱体的体积，“π”表示圆周率，大多数数学计算中它都可以设定为3.14，“r”为圆柱体底部圆形的半径，“h”表示圆柱体的高度。

圆柱体的体积可以通过该公式计算出来，结果就是体积的数值。

在计算圆柱体的体积时，首先要知道圆柱体的半径和高度，然后把它们代入到上面的公式中，算出结果。

比如，要计算一个半径为2米，高度为3米的圆柱体体积，那么可以把这两个数字代入到上面的公式中，就可以得出结果为37.68米3。

另外，圆柱体是一种特殊的体积图形，其中有一些具有特殊性质的属性，比如高度和底面半径的比，有时在计算其体积时也要考虑这些性质。

比如，一个底面半径为2米，高度为4米的圆柱体，当底面长宽比和高度长宽比不同时，那么这个圆柱体的体积也会有所不同。

最后，圆柱体是数学中一种常用的图形，其中圆柱体体积的计算也非常重要，它最常用的计算方法是使用πr2h的公式来求出体积的数值，在实际求解中有时也需要考虑底面和高度的比例关系来改变计算结果，从而准确得出结果。

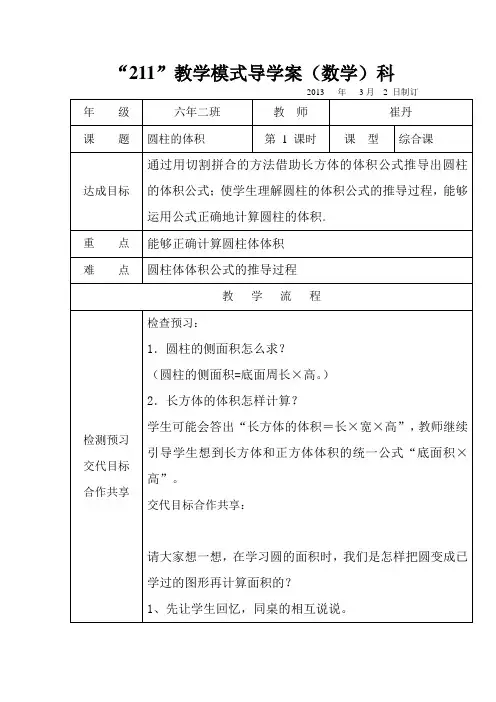
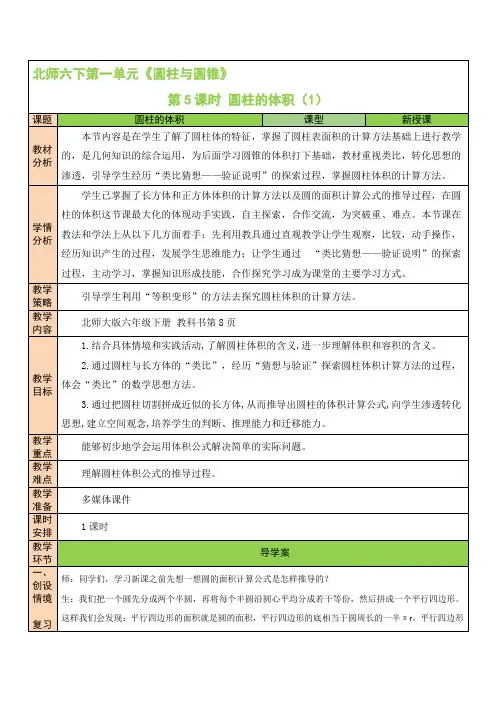
1、在一个棱长是6厘米的正方体内削一个最大的圆柱，圆柱的体积是多少立方厘米？2、在一个棱长是8厘米的正方体内削一个最大的圆柱，削去部分的体积是多少立方厘米？3、在一个长为10厘米的横截面是一个周长为16厘米的正方形的长方体中削一个最大的圆柱，削去部分的体积是多少立方厘米？4、一个底面直径为20厘米，高为10分米圆柱形水槽，把一块石块完全浸入这个水槽，水面上升了5分米，这块石块的体积是多少？（提示：放入水中物体的体积=容器的底面积×水面上升的高度）5、一个圆柱形玻璃杯底面半径是10厘米，里面装有水，水的高度是12厘米，把一小块铁块放进杯中，水上升到15厘米，这块铁块重多少克？（每立方厘米铁重7.8克）6、一个高为8分米圆柱形水槽，把一个底面直径是4厘米，高为5厘米的圆柱形石块完全浸入这个水槽，水面上升了2分米，这个水槽的底面积是多少？（提示：先求出放入物体的体积,再根据公式求：容器的底面积=放入物体的体积÷水面上升的高度）7、把一个底面积是10平方厘米，高是3.14厘米的圆柱形铁块放入一个底面半径为5厘米的圆柱形水桶内，水完全浸没铁块，且没有溢出，水面上升了多少厘米？8、一个圆柱形水槽里面有10厘米深的水，水槽底面积是144平方厘米，将一个长6厘米的正方形铁块放入水中，水面将上升多少厘米？9、一个长方形的容器，长31.4厘米，宽8厘米，水深10厘米，把一个底面半径是5厘米圆柱形铁块完全浸入容器内，水面升高了2厘米，这个圆柱形铁块的高是多少厘米？10、一个底面直径是10厘米的圆柱形水桶，水深12厘米，现把一个高是8厘米的圆柱形铁块放入水中，完全浸没且没有溢出，水深升高到15厘米，这个圆柱形铁块的底面积是多少平方厘米？11、往一个底面直径是8厘米，高是10厘米的圆柱形玻璃杯内倒入水，水面高是8厘米，把一个小球浸没在杯内，水满后还溢出12.52mL，求小球的体积？12、有一个底面直径为20厘米的圆柱形玻璃杯，里面装有一些水，已知杯中水面距杯口3厘米，若将一个圆柱形铅锤浸没水中，水会溢出20毫升，铅锤的体积是多少？13、在一个底面直径是20厘米的圆柱形容器中装有水，将一个底面直径为10厘米的圆柱形铁锤放入水中，当铁锤从圆柱形容器中取出后，水面下降1厘米，求铁锤的高？14、有一个底面半径为2厘分米的圆柱形水桶，桶内盛满水，并浸有一个底面是边长是2分米的正方形的长方体铁块。