八数码难题

八数码问题解释8数码问题又称9宫问题，源于一个古老的智力游戏。

说白了就是我们小时候玩的“华容道”。

意在给定的9格棋盘的8个格子内分别放一个符号，符号之间互不相同，剩下一格做为“出口”。

我们把8个符号在棋盘上的排列顺序称作8数码的状态，游戏要求给定一个初始的状态与一个终止状态，符号要经过若干次移动后由初态变成终态，这个过程中只有“出口”附近的符号可以朝“出口”的方向移动，且每次只能移动一个符号。

如下图所示，（其中我们用0表示出口，=》表示移动一次，=》*表示移动0-n次）：初态终态1 2 3 1 2 3 0 1 24 5 6 =》 4 5 6 =》* 3 4 57 8 0 7 0 8 6 7 82 解决方案通过观察我们可以发现每一次8数码的状态都可以通过移动字符变成有限的几种其他状态，比如上图中我们可以知道初态“出口”附近有8和6可以移动，那么这个初态可以经过移动得到两个新的状态。

我们人在玩这个游戏的时候，总是要做下面几个步骤：1．看看哪个符号可以移动。

2．判断一下哪个符号的移动最有利于到达终态。

3．选定一个符号并移动它。

4．判断是否到达终态，是则结束，否则就回到第一步。

而现在我们要使用机器来模拟这一过程，其步骤与人类类似，但不同的是，人在执行第二部的时候总是能预先判断未来好几步的局势，从而选出最有利的一步，而机器则不行，它要先得到一个状态才能知道这个状态下一步将会到哪些状态而无法像我们一样一次就看到后面几步的状态。

那么基本思想就是让机器穷尽由初态出发到达所有可能状态的路径，并从中找到有终态的路径作为问题的解。

2.1 A*算法就如我们上面说到的让机器找出所有的可能来得到问题的解，看起来似乎很简单，但问题在于一旦8数问题的解达到一定规模，机器所要穷尽的路径数量将变得极为庞大，无疑会消耗大量的时间和空间。

那么如何让机器像人一样在选择移动符号的时候总是能选择最有利的那一个呢？下面就要介绍启发式搜索中的一个算法A*算法来解决这个问题。

八数码问题实验报告八数码问题实验报告引言：八数码问题是一种经典的数学难题，在计算机科学领域有着广泛的研究和应用。

本实验旨在通过探索八数码问题的解法，深入理解该问题的本质，并通过实验结果评估不同算法的效率和准确性。

一、问题描述：八数码问题是一个在3×3的棋盘上，由1至8的数字和一个空格组成的拼图问题。

目标是通过移动棋盘上的数字，使得棋盘上的数字排列按照从小到大的顺序排列，最终形成如下的目标状态：1 2 34 5 67 8二、解法探索：1. 深度优先搜索算法：深度优先搜索算法是一种经典的解决拼图问题的方法。

该算法通过不断尝试所有可能的移动方式，直到找到目标状态或者无法再继续移动为止。

实验结果显示，该算法在八数码问题中能够找到解，但由于搜索空间庞大，算法的时间复杂度较高。

2. 广度优先搜索算法：广度优先搜索算法是另一种常用的解决八数码问题的方法。

该算法通过逐层扩展搜索树，从初始状态开始，逐步扩展所有可能的状态，直到找到目标状态。

实验结果显示，该算法能够找到最短路径的解，但同样面临搜索空间庞大的问题。

3. A*算法：A*算法是一种启发式搜索算法，结合了深度优先搜索和广度优先搜索的优点。

该算法通过使用一个估价函数来评估每个搜索状态的优劣，并选择最有希望的状态进行扩展。

实验结果显示，A*算法在八数码问题中表现出色，能够高效地找到最优解。

三、实验结果与分析：通过对深度优先搜索、广度优先搜索和A*算法的实验，得出以下结论：1. 深度优先搜索算法虽然能够找到解，但由于搜索空间庞大，时间复杂度较高，不适用于大规模的八数码问题。

2. 广度优先搜索算法能够找到最短路径的解，但同样面临搜索空间庞大的问题，对于大规模问题效率较低。

3. A*算法在八数码问题中表现出色，通过合理的估价函数能够高效地找到最优解，对于大规模问题具有较好的效果。

四、结论与展望：本实验通过对八数码问题的解法探索，深入理解了该问题的本质，并评估了不同算法的效率和准确性。

用A*算法解决八数码问题一、 题目：八数码问题也称为九宫问题。

在3×3的棋盘，有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。

棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。

要解决的问题是：任意给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

二、 问题的搜索形式描述状态：状态描述了8个棋子和空位在棋盘的9个方格上的分布。

初始状态：任何状态都可以被指定为初始状态。

操作符：用来产生4个行动（上下左右移动）。

目标测试：用来检测状态是否能匹配上图的目标布局。

路径费用函数：每一步的费用为1，因此整个路径的费用是路径中的步数。

现在任意给定一个初始状态，要求找到一种搜索策略，用尽可能少的步数得到上图的目标状态算法介绍三、 解决方案介绍1.A*算法的一般介绍A*（A-Star)算法是一种静态路网中求解最短路最有效的方法。

对于几何路网来说，可以取两节点间欧几理德距离（直线距离）做为估价值，即()()()()()()**f g n sqrt dx nx dx nx dy ny dy ny =+--+--；这样估价函数f 在g 值一定的情况下，会或多或少的受估价值h 的制约，节点距目标点近，h 值小，f 值相对就小，能保证最短路的搜索向终点的方向进行。

明显优于盲目搜索策略。

A star算法在静态路网中的应用2.算法伪代码创建两个表，OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。

算起点的估价值，将起点放入OPEN表。

while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X){算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值 ){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE){if( X的估价值小于CLOSE表的估价值 ){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。

八数码问题
八数码问题是一个经典的问题，也称为滑动谜题。

问题的描述是：在一个3x3的棋盘上，有1-8这8个数字和一个空格组成的九个格子，目标是通过移动数字，将棋盘上的数字按从小到大的顺序排列，空格在最后一个位置。

解决这个问题的算法主要有搜索算法，其中最常见的是A*算法。

A*算法是一种启发式搜索算法，通过建立一个状态空间图，并使用启发式函数估算每个状态到目标状态的距离，来优化搜索过程。

在八数码问题中，启发式函数可以使用曼哈顿距离来估算。

另外，也可以使用深度优先搜索、广度优先搜索、IDA*等搜索算法来解决八数码问题。

这些算法在搜索过程中以不同的方式遍历状态空间图，找到最优解。

解决八数码问题的具体步骤一般如下：
1. 定义初始状态和目标状态。

2. 使用搜索算法进行搜索，找到从初始状态到目标状态的最优解。

3. 在搜索过程中，需要注意状态的合法性和重复状态的处理。

4. 输出最优解，即一系列移动操作，将初始状态转化为目标状态。

需要注意的是，八数码问题可能存在无解的情况，需要在搜索过程中判断并处理无解情况。

此外，由于八数码问题的状态空间较大，搜索过程可能需要一定的时间和空间复杂度。

因此，在实现解决算法时，需要考虑性能优化的问题。

实验报告课程名称人工智能_____________实验项目八数码难题______________实验仪器电脑、visual C++_________系别____________ 专业__ _____班级/学号学生姓名_ _________实验日期____成绩_______________________指导教师_________一、实验目的理解并熟悉掌握深度优先搜索和广度优先搜索地方法。

二、实验内容九宫格中有8个数码，其中只有一个空，规则是只能把一个数码移动到空的格子中，要求从一个初始状态移动到一个目标状态所要花费的最少步数【算法分析】解决此类问题的办法是宽度搜索，深度搜索耗时太大无法接受。

当需要移动的步数很多时，普通的宽度搜索仍旧无法满足需要，需要对其进行优化。

这个问题也可以推广到流行的拼图游戏。

【具体步骤】一、确定问题规模（考虑搜索的时间代价）二、确定产生式规则（如果规则太多，则时间代价会很大）三、套用经典宽度搜索框架写程序三、代码和结果#include <stdlib.h>#include <stdio.h>typedef struct Node {int num[9]; //棋盘状态int deepth; //派生的深度g(n)int diffnum; //不在位的数目h(n)int value; //耗散值f(n)=g(n)+h(n)struct Node * pre;struct Node * next;struct Node * parent;}numNode; /* ---------- end of struct numNode ---------- */int origin[9]; //棋盘初始状态int target[9]; //棋盘目标状态int numNode_num,total_step;numNode *open,*close; //Open表和Close表numNode *create_numNode(){return (numNode *)malloc(sizeof(numNode));}numNode *open_getfirst(numNode *head); //返回第一项，并从Open表中删除void open_insert(numNode *head,numNode *item); //向Open表中按序插入新节点void close_append(numNode *head,numNode *item); //向Close表中插入新节点int expand(numNode *item); //扩展节点int print_result(numNode *item); //打印结果numNode *copy_numNode(numNode *orgin);char isNewNode(numNode *open,numNode *close,int num[9]);//是否在Open表或Close表中void print_num(int num[9]); //打印棋盘状态int diff(int num[9]); //求不在位棋子的个数void init(); //初始化，获得棋盘初始状态和目标状态void swap(int *a,int *b);int operate(int num[],int op);void free_list(numNode *head);/** === FUNCTION ======================================================================* Name: 主函數* Description: 程序入口*=============================================================================== ======*/intmain ( int argc, char *argv[] ){//初始化Open表和Close表open=create_numNode();close=create_numNode();open->pre=open->next=close->pre=close->next=NULL;init(); //由用户输入初始和目标状态//初始化初始节点numNode *p1;p1=create_numNode();p1->parent=NULL;p1->deepth=0;int i=0;for ( i=0; i<9; i++){p1->num[i]=origin[i];}open_insert(open,p1);numNode_num=1;p1=open_getfirst(open);while (p1!=NULL){close_append(close,p1);if(expand(p1))return EXIT_SUCCESS;p1=open_getfirst(open);}printf("No solution!\n");return EXIT_SUCCESS;} /* ---------- end of function main ---------- */voidinit ( ){while(1){printf("Please input opriginal status:\nFor example:123456780 stands for\n""1 2 3\n""4 5 6\n""7 8 0\n");char temp[10];scanf("%s",&temp);int i=0;for ( i=0;i<9 && temp[i]-'0'>=0 && temp[i]-'0'<=8; i++) {origin[i]=temp[i]-'0';}printf("Please input target status:\n");scanf("%s",&temp);int j=0;for ( j=0; j<9 && temp[j]-'0'>=0 && temp[j]-'0'<=8; j++){target[j]=temp[j]-'0';}system("cls");if ( i==9&&j==9){break;}}} /* ----- end of function init ----- */voidopen_insert (numNode *head,numNode *item){numNode *p,*q;p=head->next;q=head;while ( p!=NULL && item->value > p->value ){q=p;p=p->next;}q->next=item;item->pre=q;item->next=p;if(p!=NULL){p->pre=item;}} /* ----- end of function open_insert ----- */numNode *open_getfirst (numNode *head){numNode *p;if ( head->next == NULL ){return NULL;}p=head->next;head->next=p->next;if ( p->next != NULL ){p->next->pre=head;}p->pre=NULL;p->next=NULL;return p;} /* ----- end of function open_getfirst ----- */voidclose_append (numNode *head,numNode *item) {item->next=head->next;item->pre=head;head->next=item;if ( item->next!=NULL ){item->next->pre=item;}} /* ----- end of function close_append ----- */intexpand (numNode *p1){numNode * p2;int op=1;for ( op=1; op<=4; op++){p2=copy_numNode(p1);operate(p2->num,op);if(isNewNode(open,close,p2->num)=='N'){p2->parent=p1;p2->deepth=p1->deepth+1;p2->diffnum=diff(p2->num);p2->value=p2->deepth+p2->diffnum;if(p2->diffnum==0){total_step=print_result(p2);printf("Total step: %d\n",total_step);free_list(open);free_list(close);return 1;}else{numNode_num++;open_insert(open,p2);}}elsefree(p2);}return 0;} /* ----- end of function expand ----- */intoperate(int m[], int op){int blank;blank=0;while (m[blank]!=0 && blank<9 )++blank;if (blank==9)return 1;switch (op) {case 1: /* up */if (blank>2)swap(m+blank,m+blank-3);break;case 2: /* down */if (blank<6)swap(m+blank,m+blank+3);break;case 3: /* left */if (blank!=0 && blank!=3 && blank!=6)swap(m+blank,m+blank-1);break;case 4: /* right */if (blank!=2 && blank!=5 && blank!=8)swap(m+blank,m+blank+1);break;default : return 1;}return 0;}voidswap(int *a, int *b){int c;c=*a;*a=*b;*b=c;}numNode *copy_numNode (numNode *origin){numNode *p;p=create_numNode();p->deepth=origin->deepth;p->diffnum=origin->diffnum;p->value=origin->value;int i;for ( i=0; i<9; i++){(p->num)[i]=(origin->num)[i];}return p;} /* ----- end of function copy_numNode ----- */intdiff (int num[9]){int i,diffnum=0;for(i=0;i<9;i++)if(num[i]!=target[i])diffnum++;return diffnum;} /* ----- end of function diff ----- */charisNewNode (numNode *open,numNode *close,int num[9]) {numNode *p;int i=0;p=open->next;while ( p!=NULL ){for ( i=0; i<9; i++){if(p->num[i]!=num[i])break;}if(i==9)return 'O'; //Openp=p->next;}p=close->next;while ( p!=NULL ){for ( i=0; i<9; i++){if(p->num[i]!=num[i])break;}if(i==9)return 'C'; //Closep=p->next;}return 'N';} /* ----- end of function isNewNode ----- */voidfree_list (numNode *head){numNode *p,*q;p=head->next;while ( p!=NULL ){q=p->next;free(p);p=q;}free(head);} /* ----- end of function free_list ----- */voidprint_num (int num[9]){int i;for ( i=0; i<9; i++){printf("%d\t",num[i]);if((i%3)==2)printf("\n");}} /* ----- end of function print_num ----- */intprint_result ( numNode *item){numNode *p;int step;p=item;if(p!=NULL){step=print_result(p->parent);printf("\nStep %d:\n",step+1);print_num(p->num);return step+1;}else{return -1;}}四．实验心得这次试验让我更加深入了解了什么是人工智能，让我了解了人工智能的作用以及含义和人工智能的使用范围以及对于我们未来生活得作用的广大。

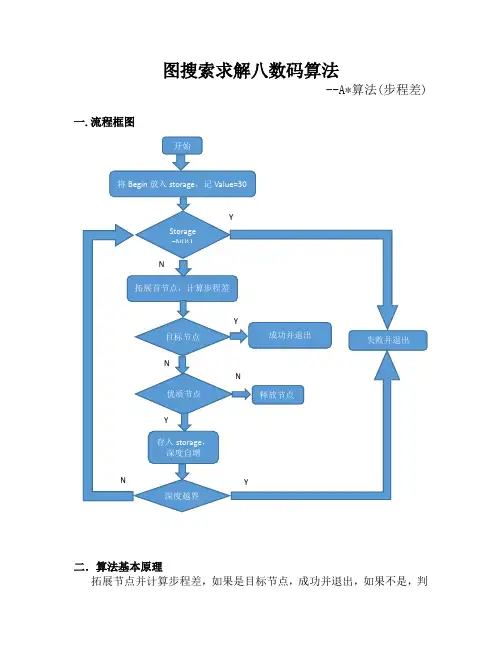
图搜索求解八数码算法--A*算法(步程差) 一.流程框图二．算法基本原理拓展节点并计算步程差，如果是目标节点，成功并退出，如果不是，判断是否为优质节点，是则拓展为子节点，否则舍弃；判断深度是否越界，是则失败，未越界则继续拓展节点，若拓展表为空，则失败退出。

八数码结构体由矩阵Array，步程差Value，屏蔽方向Undirect和父节点指针*parent四部分组成，Array存放矩阵数字状态，Value存放估值函数值，Undirect记录上一步移动方向避免逆推，*parent记录父子关系用于寻径。

三．模块分析Getgraph 键盘输入获得初始数码组并返回Graph结构体指针。

Printgraph 输入八数码结构体地址，打印矩阵数字状态与当前步程差。

Evaluate 输入目标矩阵与当前矩阵，计算步程差并返回值。

Move 输入当前矩阵与移动方向Direct，移动并返回新结构体地址。

Search 输入起始结构体与目标结构体，尝试寻径并记录路径并返回终点地址（若成功）或返回空指针（若失败）。

Main 主函数，定义目标矩阵并调用函数。

四．源代码// Eight-figure puzzle// A*#include"stdafx.h"#include<stdio.h>#include<stdlib.h>#define N 3 //数码组长度#define MAX 50 //最大搜索深度typedefstruct node//八数码结构体{int array[N][N];//数码组int Value;//评估值int Undirect;//所屏蔽方向，防止往回推到上已状态，1上2下3左4右struct node *parent;//父节点}Graph;Graph *Storage[MAX]; //拓展节点存储队列Graph *path[MAX]; //路径堆栈Graph *GetGraph(Graph *New_graph) ////////自定义初始数码组{int x;for (x = 0; x <N; x++){scanf("%d %d %d", &New_graph->array[x][0], &New_graph->array[x][1],&New_graph->array[x][2]);}New_graph->Value = 30;New_graph->Undirect = 0;New_graph->parent = NULL;return New_graph;}void PrintGraph(Graph *point_graph) /////////打印数码组{int i, j;if (point_graph == NULL)printf("NULL\n");else{printf(" ---------------\n");for (i = 0; i<N; i++){printf("| ");for (j = 0; j<N; j++){printf("%d ", point_graph->array[i][j]);}printf("|");if (i==N-1)printf(" Value %d ", point_graph->Value);//评估函数值printf("\n");}printf(" ---------------\n");}}int Evaluate(Graph *point_graph, Graph *End_graph) /////////评价函数{int value = 0;//评估值int i, j,m ,n ;for (i = 0; i<N; i++){for (j = 0; j<N; j++){for (m = 0; m <N; m++){for (n = 0; n <N; n++){if (point_graph->array[i][j] == End_graph->array[m][n])value = value + abs(i - m) + abs(j - n); //数字当前位置与目标位置步程差之和}}}}point_graph->Value = value;return value;}Graph *Move(Graph *point_graph, int Direct) /////////移动数码组{Graph *New_graph;int BlankLocate = 0;//定位空格指示int Movable = 1;//移动有效int i, j, x0, y0, x, y;for (i = 0; i<N; i++)//空格坐标i,j{for (j = 0; j<N; j++){if (point_graph->array[i][j] == 0){BlankLocate = 1;break;}}if (BlankLocate == 1)break;}x0 = i;y0 = j;switch (Direct){case 1://上x0--;if (x0<0)Movable = 0;break;case 2://下x0++;if (x0 >= N)Movable = 0;break;case 3://左y0--;if (y0<0)Movable = 0;break;case 4://右y0++;if (y0 >= N)Movable = 0;break;}if (Movable == 0)//不能移动则返回原节点return point_graph;New_graph = (Graph *)malloc(sizeof(Graph));//生成节点for (x = 0; x<N; x++){for (y = 0; y<N; y++){New_graph->array[x][y] = point_graph->array[x][y];//复制数码组}}New_graph->array[i][j] = New_graph->array[x0][y0];New_graph->array[x0][y0] = 0;return New_graph;}Graph *Search(Graph *Begin, Graph *End) /////////搜索函数{Graph *St1, *St2, *ta;int Step = 0;//深度int Direct = 0;//方向int i;int front, rear;front = rear = -1;//队列初始化ta = NULL;rear++;//入队Storage[rear] = Begin;while (rear != front)//队列不空{front++;//出队St1 = Storage[front];for (i = 1; i <= 4; i++)//分别从四个方向推导出新子节点{Direct = i;if (Direct == St1->Undirect)//跳过屏蔽方向continue;St2 = Move(St1, Direct);//移动数码组if (St2 != St1)//数码组是否可以移动{Evaluate(St2, End);//评价新的节点sif (St2->Value == 0)//为0则搜索完成{St2->parent = St1;rear++;Storage[rear] = St2;//存储节点到待处理队列ta = St2;break;}if (St2->Value <= St1->Value + 1){St2->parent = St1;//st2->Undirect=Direct>2?(Direct==3)+3:(Direct==1)+1;/屏蔽方向switch (Direct)//设置屏蔽方向，防止往回推{case 1://上St2->Undirect = 2;break;case 2://下St2->Undirect = 1;break;case 3://左St2->Undirect = 4;break;case 4://右St2->Undirect = 3;break;}rear++;Storage[rear] = St2;//存储节点到待处理队列}else{free(St2);//抛弃劣质节点St2 = NULL;}}}if (ta != NULL)//为0则搜索完成break;Step++;//统计深度if (Step>=MAX){break;}}return ta;}int main(int argc, constchar * argv[]){// 8 1 3 7 4 5 6 2 0// 4 1 3 2 7 5 8 0 6// 4 5 1 2 7 3 0 8 6 //16 steps in fact but failed//目标数码组Graph End_graph = {{{ 1, 2, 3 },{ 8, 0, 4 },{ 7, 6, 5 }}, 0, 0, NULL};//初始数码组Graph New_graph;Graph *Begin_graph;printf("Enter initial matrix line by line\n For example:\t1 3 4 ENTER\n\t\t8 2 5 ENTER\n\t\t7 6 0 ENTER\n\n");Begin_graph = GetGraph(&New_graph);Evaluate(Begin_graph, &End_graph);printf("Initial matrix:\n");PrintGraph(Begin_graph);printf("Target matrix:\n");PrintGraph(&End_graph);Graph *W, *P;int top = -1;//图搜索W = Search(Begin_graph, &End_graph);if (W){P = W; //压栈while (P != NULL){top++;path[top] = P;P = P->parent;}printf("<<<<<< The Path >>>>>>\n");//弹栈打印while (top>-1){P = path[top];top--;PrintGraph(P);}printf("<<<<< Mission Complete >>>>>\n");system("pause");}else{printf("Path not found ,Search depth is %d\n", MAX);system("pause");}return 0;}五．运行结果将初始数码组改写为 2 5 4 3 7 1 8 6 ，定义某个数前面比他小的数个数为Xi,所有数字的Xi相加为Y，因为四向移动只可能改变Y的大小，不改变其奇偶性。

《人工智能初步》的一个案例：八数码难题及其状态空间表示法各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢2、引导学生思考问题，并得到结论。

思考问题，并在教师的引导下得出如下结论：（1）使用计算机解决问题的一般思路如下：问题→算法→程序设计。

其关键在于根据人类解决问题的经验来得到求解问题的算法。

（2）对于某些问题，得出其就解算法较容易，而对于较难问题，则不然。

此时，需要研究人类处理该为问题的经验，并加以总结才能提升为算法。

1、八数码难题介绍八数码难题的游戏规则，并给出棋盘的初始状态和目标状态。

要求能使用尽可能少的棋步从棋盘的初始状态走到目标状态。

（假设，要求能在4步内解决问题）——提出问题：要使用计算机来求解八数码难题，首先应该做什么？学生明确要得到求解问题的算法，首先需要研究人类是如何求解该问题的，自己是如何求解该问题的、同学是如何求解该问题的。

带着这些问题，动手实践；1、按游戏规则，从棋盘的初始状态开始移动棋子，记录移动4步棋子的过程。

2、学生分组讨论，比较每个人的移动结果，得出不同的移动过程。

2、八数码难题的状态空间表示提问1：能否把小组中在4步所有走法用一棵树表示出来？提问2：能否把在4步内所有可能的走法使用一棵树表示出来？教师引导学生问题上述问题。

每小组学生把本组所有的结果汇总，并使用一棵树来表示出来。

将一个小组的结果展示出来，其它小组补充，最后形成一棵走4步棋的完整的状态空间树。

3、状态空间树的作用提问1：状态空间树有什么作用？提问2：树中节点和边的含义？提问3：如何要画出10个、20个棋步内对应的状态空间树？学生根据实践，在教师引导下得出：状态空间树表示出了移动4步情况下所有可能的走棋情况。

4、状态空间的概念及有关术语：状态、操作、初始状态、目标状态。

三元组表示。

根据由上述问题2和问题3来体会这些概念小结1、状态空间表示法的基本思想及意义。

2、挖掘其技术思想，对学生进行情感价值观、技术思想的教育：以少表示多，以有穷表示无穷。

实验三：A*算法求解8数码问题实验一、实验目的熟悉和掌握启发式搜索的定义、估价函数和算法过程，并利用A*算法求解N数码难题，理解求解流程和搜索顺序。

二、实验内容1、八数码问题描述所谓八数码问题起源于一种游戏:在一个3×3的方阵中放入八个数码1、2、3、4、5、6、7、8，其中一个单元格是空的。

将任意摆放的数码盘（城初始状态）逐步摆成某个指定的数码盘的排列（目标状态），如图1所示：图1 八数码问题的某个初始状态和目标状态对于以上问题，我们可以把数码的移动等效城空格的移动。

如图1的初始排列，数码7右移等于空格左移。

那么对于每一个排列，可能的一次数码移动最多只有4中，即空格左移、空格右移、空格上移、空格下移。

最少有两种（当空格位于方阵的4个角时）。

所以，问题就转换成如何从初始状态开始，使空格经过最小的移动次数最后排列成目标状态。

2、八数码问题的求解算法盲目搜索宽度优先搜索算法、深度优先搜索算法启发式搜索启发式搜索算法的基本思想是：定义一个评价函数f，对当前的搜索状态进行评估，找出一个最有希望的节点来扩展。

先定义下面几个函数的含义：f*(n)=g*(n)+h*(n) (1)￥式中g*(n)表示从初始节点s到当前节点n的最短路径的耗散值；h*(n)表示从当前节点n到目标节点g的最短路径的耗散值，f*(n)表示从初始节点s经过n到目标节点g的最短路径的耗散值。

评价函数的形式可定义如(2)式所示：f(n)=g(n)+h(n) (2)其中n是被评价的当前节点。

f(n)、g(n)和h(n)分别表示是对f*(n)、g*(n)和h*(n)3个函数值的估计值。

利用评价函数f(n)=g(n)+h(n)来排列OPEN表节点顺序的图搜索算法称为算法A。

在A算法中，如果对所有的x，h(x)<=h*(x) (3)成立，则称好h(x)为h*(x)的下界，它表示某种偏于保守的估计。

采用h*(x)的下界h(x)为启发函数的A算法，称为A*算法。

人工智能实验报告学院：信息科学与工程学院班级：自动化0901班学号： 06姓名：孙锦岗指导老师：刘丽珏日期：2011年12月20日一、实验名称、目的及内容实验名称：八数码难题的搜索求解演示实验目的：加深对图搜索策略概念的理解，掌握搜索算法。

实验内容要求：以八数码难题为例演示广度优先或深度优先搜索、A算法（本实验使用的是广度优先搜索）的搜索过程，争取做到直观、清晰地演示算法。

八数码难题：在3×3方格棋盘上，分别放置了标有数字1,2,3,4,5,6,7,8的八张牌，初始状态S0，目标状态如图所示，可以使用的操作有:空格上移，空格左移，空格右移，空格下移。

试编一程序实现这一搜索过程。

二、实验原理及基本技术路线图实验原理：八数码问题中，程序产生的随机排列转换成目标共有两种可能，而且这两种不可能同时成立，也就是奇数排列和偶数排列。

我们可以把一个随机排列的数组从左到右从上到下用一个数组表示，例如｛８，７，１，５，２，６，３，４，０｝其中０代表空格。

它在奇序列位置上。

在这个数组中我们首先计算它能够重排列出来的结果，公式就是：∑（Ｆ（Ｘ））＝Ｙ，其中Ｆ（Ｘ），就是一个数他前面比这个数小的数的个数，Ｙ为奇数和偶数个有一种解法。

那么上面的数组我们就可以解出它的结果。

数据结构：本实验使用的数据结构是队列，应用队列先进先出的特点来实现对节点的保存和扩展。

首先建立一个队列，将初始结点入队，并设置队列头和尾指，然后取出队列（头指针所指）的结点进行扩展，从它扩展出子结点，并将这些结点按扩展的顺序加入队列，然后判断扩展出的新结点与队列中的结点是否重复，如果重复则，否则记录其父结点，并将它加入队列，更新队列尾指针，然后判断扩展出的结点是否是目标结点，如果是则显示路径，程序结束。

否则如果队列头的结点可以扩展，直接返回第二步。

否则将队列头指针指向下一结点，再返回第二步，知道扩展出的结点是目标结点结束，并显示路径。

算法分析：九宫问题的求解方法就是交换空格（０）位置，直至到达目标位置为止。

一、八数码游戏问题简介九宫排字问题(乂称八数码问题)是人工智能当中有名的难题之一。

问题是在3X3方格盘上，放有八个数码，剩下第九个为空，每一空格其上下左右的数码可移至空格。

问题给定初始位置和目标位置，要求通过一系列的数码移动，将初始位置转化为目标位置。

八数码游戏二、实验目的1 .熟悉人工智能系统中的问题求解过程；2 .熟悉状态空间的盲目搜索和启发式搜索算法的应用;3 .熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验的思路八数码问题：在3X3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如:实验八数码游戏问题(a)初始状态图 (b)目标状态图1八数码问题示意图1 .启发函数设定由八数码问题的部分状态图可以看出，从初始节点开始，在通向目标节点的路径上，各节点的数码格局同目标节点相比较，其数码不同的位置个数在逐渐减少，最后为零，因此可以把数码不同的位置个数作为标志一个节点到目标节点距离远近的一个启发性信息，利用这个信息来扩展节点的选择，减少搜索范围，提高搜索速度。

2 .搜索过程：（搜索采用广度搜索方式，利用待处理队列辅助，逐层搜索（跳过劣质节点））a 、把初始数码组压入队列；b 、从队列中取出一个数码组节点；c 、扩展子节点，即从上下左右四个方向移动空格，生成相应子节点：d 、对子节点数码组作评估，是否为优越节点，即其评估值是否小于等于其父节点加一，是则将其压入队，否则抛弃。

e 、判断压入队的子节点数码组（优越点）的评估值，为零则表示搜索完成，退出搜索；f 、跳到步骤2；四、数据结构的设计//八数码结构体 〃数码组 〃评估值，差距 〃所屏蔽方向，防止往回推到上一状态,1上2下3左4 〃父节点数码结构体typedefstnictnode(intfonn[N][N];intevalue;intudirec;右stmctnode"parent;}Graph;Giaph*Qu[MAX];〃队歹lj起始五、实验过程及代码#mclude<stdio.h>}〃设计了搜索深度范围，防止队列内存越界#include<stdlib.h>#include<tnne.h>#defineN3〃数码组大小#defineMax_Step50〃最大搜索深度#defineMAX50typedefstinctnode//八数码结构体{intform[N][N];〃数码组intevahie;//评估值intudirect;〃所屏蔽方向，防止往回推到上已状态，1上2下3左4右stiuctnode*parent;〃父节点}Graph;Graph*Qu[MAX];//队歹ijGi-aph*St[MAX];〃堆栈〃/〃/〃/打印数码组voidPrint(Graph*The_graph){mtij;if(The_gi-aph=NULL)pnntf(”图为空\n)else{pnntff\n M);for(i=0;i<N;i++)(pmitf(n|\t H);for(j=0;j<N;j++)(printff^d't'Thjgraph->fbrm[i][j]);〃遍历打印}pinitfC,\t|\n n);}pniitf(n|\t\t\t差距:%d\t|\ir：The_graph->evahie);//差距显示pnntff\n M); ))〃//〃/〃评价函数mtEvaluate(Graph*The_gi'aph,Graph*End_graph){int\T alute=O;//差E巨数mtij;fbr(i=O;i<N;i-H-){for(j=0;j<N;j++)(if(The_graph->fbmi[i]|j]!=End_gi'aph->fonn[i][j])(valute++;}}}The_giaph->evalue=x r alute;returnvalute;}/〃/〃/〃移动数码组Graph*Move(Graph*Tlie_gi'aph,mtDirect,intCreatNew_graph){ Graph*New_graph;intHasGetBlank=O;〃是否获取空格位置intAbleMove=1;〃是否可移动intfor(i=0;i<N;i++)〃获取空格坐标ij{for(j=0;j<N;j++)(if(The_graph->fbim[i][j]=0)(HasGetBlaiik=l;break;}}if(HasGetBlank=l)break;}〃prin氓”空格位置:%d,%d\n”,i,j);t户U=J；〃移动空格switch(Direct){case1://_Etj-sif(t_i<0)AbleMove=0;break;case27/Ft_i++;if(t_i>=N)AbleMove=0;break;case3://左if(U<o)AbleMove=0;break;case4://右tj++;if(tj>=N)AbleMove=0;break;}if(AbleMove==0)〃不能移动则返回原节点{returnThe_graph;)if(CreatNew_gi,aph=1){New_graph=(Graph*)malloc(sizeof(Graph));//生成节点for(x=0;x<N;x++)( fbr(y^O;y<N;y++)(New_gi,aph->fbnn[x][y]=The_graph->fomi[x][y];//目制数码组}})elseNew_graph=The_graph;}〃移动后New_graph->fdmi[i][j]=New_gi-aph->fbnn[t_i][tj];New_graph->fbnn[t_i][t_j]=O;//pnntf("移动产生的新图:\n");//Print(New_graph);retiimNew_graph;}/〃/〃/〃搜索函数Graph*Search(Graph"Begin,Graph*End){Graph*gl,*g2,*g;intStep=O;〃深度intDirect=O;〃方向inti;intfront,rear;fiont=i-eai--l-Jf队列初始化g=NULL;reai++;〃入队Qu[rear]=Begin;while(rear!=fixmt)〃队列不空{fhmHT;〃出队gl=Qu[front];“printf("开始第％d个图ont);//Pimt(gl);for(i=1;iv=4;i++)〃分别从四个方向推导出新子节点(Duect=i;if(Du-ect=g1->udirect)〃跳过屏蔽方向contmue;g2=Move(gl,Direct,1)；〃移动数码组if(g2!=gl)〃数码组是否可以移动(〃可以移动Evahiate(g2,End);〃评价新的节点〃pnntf("开始产生的第％d个图://Print(g2);if(g2->evalue<=gl->evalue+1)〃是优越节点g2->parent=gl;〃移动空格switch(Direct)〃设置屏蔽方向，防止往回推(case1://Jtg2->udirect=2;break;case2:〃下g2->udu,ect=l;break;case3:〃左g2->udkect=4;break;case4:〃右g2->udirect=3;break;)rear4-+;Qu[rear]=g2;〃存储节点到待处理队列if(g2->evalue==0)〃为0则搜索完成(g=g2；//i=5;break;)}else(丘ee(g2);〃抛弃劣质节点g2=NULL;})}if(g!=NULL)〃为0则搜索完成(if(g->evalue==O)break;Step++;〃统计深度if(Step>Max_Step)break;}}retiinig;}mtmam(mtargc?constchar*argv口){//insertcodehere...GraphBegm_graph={{{2,8,3},{1,6,4},{7,0,5}},0,0,NULL)；/*IGraphBegm_graph={{{2,8,3},{1,0,4},{7,6,5}},0,0,NULL)；GraphBegm_graph={{{2,0,1},{4,6,5},{3,7,8}},0,0,NULL)；*/〃目标数码组GraphEnd_graph={{{1,2,3},{8,0,4},{7,6,5}},0,0,NULL)；Evaluate(&Begin_gi,aph,&End_graph);//对初始的数码组评价pnntf("初始数码组:\n”)；Pnnt(&Begm_graph);pnntf("目标数码组An")；Pnnt(&End_giaph);Graph*G,*P:inttop=-l;〃图搜索G=Search(&Begm_graph,&End_graph);〃打印if(G){〃把路径倒序P=G;〃压栈while(P!=NULL)(top++;St[top]=P;P=P->parent;}pnntf(y<v<vvvvvvvvvvv搜索结^»»»»»»»»\ii H);〃弹栈打印while(top>-l)(P=St[top];top--;Prmt(P);}pniitf(n<««««««««^Mc»»»>»»»»»>^i n);}else{prmtf("搜索不到结果，深度为％dW,Max_Step);〃设计搜索深度范围主要是防止队列内存越界)retiim0;六、实验结果。

人工智能基础大作业----八数码难题学院:数学与计算机科学学院2016.12.20一、实验名称八数码难题的启发式搜索二、实验目的八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

要求：1.熟悉人工智能系统中的问题求解过程；2.熟悉状态空间的启发式搜索算法的应用；3.熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验设备及软件环境1.实验编程工具：VC++ 6.02.实验环境：Windows7 64位四、实验方法：启发式搜索1.算法描述1.将S放入open表，计算估价函数f(s)2.判断open表是否为空，若为空则搜索失败，否则，将open表中的第一个元素加入close表并对其进行扩展（每次扩展后加入open表中的元素按照代价的大小从小到大排序，找到代价最小的节点进行扩展）注：代价的计算公式f(n)=d(n)+w(n).其中f(n)为总代价，d(n)为节点的度，w(n)用来计算节点中错放棋子的个数。

判断i是否为目标节点，是则成功，否则拓展i，计算后续节点f(j)，利用f(j)对open表重新排序2.算法流程图：3.程序源代码：# include<stdio.h># include<string.h># include<malloc.h># include<stdlib.h>typedef struct node {int i,cost,degree,exp,father;int a[3][3];struct node *bef,*late;struct node *son;}treenode;int flag=0,count=1,num=0,i=0;void set(treenode *s);void cpynode(treenode *s1,treenode *s2);void add1(treenode *s,treenode *open);void adjust1(treenode *close);void jscost(treenode *s);void tiaozheng(treenode *open);void sortopen(treenode *open);int test(treenode *s1,treenode *s2);void position(treenode *s,treenode *open,treenode*close,treenode *s1);void printstr(treenode *open);int search(treenode *s1,treenode *s2);void input(treenode *s);int cmpnode(treenode *s1,treenode *s2);void print(treenode *s);void add(treenode *s,treenode *close);void xuhao(treenode *s);void extend(treenode *r1,treenode *s,treenode *s1,treenode *open,treenode *close);void main() {treenode *s0,*s1,*s;treenode *open,*close,*opend,*closed;open=(treenode*)malloc(sizeof(treenode));close=(treenode*)malloc(sizeof(treenode));open->late=NULL;close->late=NULL;opend=open;closed=close;s0=(treenode*)malloc(sizeof(treenode));set (s0);s1=(treenode*)malloc(sizeof(treenode));set(s1);printf("请输入八数码的初始状态：（以空格为分隔）\n");input (s0);printf("请输入八数码的目标状态：（以空格为分隔）\n");input(s1);xuhao(s0);add (s0,opend);while(open->late!=NULL && flag==0) {s=(treenode*)malloc(sizeof(treenode));cpynode(s,open->late);open=open->late;add(s,close);if(test(s,s1)==0){flag=1; }else{position(s,open,close,s1);sortopen(open); };};if(open->late!=NULL) {printf("搜索过程如下：\n ");adjust1(close);printstr(close);printf("\n%d 步,%d 个节点\n",num,count);} else {printf("查找错误 ! \n");}; }void set(treenode *s) {s->i=i;s->father=0;s->degree=0;s->bef=NULL;s->son=NULL;s->late=NULL; };void input(treenode *s) {int j,k;for(j=0;j<3;j++)for(k=0;k<3;k++)scanf("%d",&s->a[j][k]); };int cmpnode(treenode *s1,treenode *s2){ int j,k;for(j=0;j<3;j++)for(k=0;k<3;k++) {if(s1->a[j][k]!=s2->a[j][k])return 0; };return 1; }int test(treenode *s1,treenode *s2) { int j,k,n=0;for(j=0;j<3;j++)for(k=0;k<3;k++) {if(s1->a[j][k]!=s2->a[j][k])n++; };s1->exp=n;return n; };void xuhao(treenode *s) {i++;s->i=i; }void cpynode(treenode *s1,treenode *s2) { int j,k;for(j=0;j<3;j++)for(k=0;k<3;k++)s1->a[j][k]=s2->a[j][k];s1->bef=s2->bef;s1->cost=s2->cost;s1->exp=s2->exp;s1->degree=s2->degree;s1->i=s2->i;s1->father=s2->father; };void print(treenode *s) {int j,k;for(j=0;j<3;j++) {for(k=0;k<3;k++) {printf("%2d",s->a[j][k]); }if(j==1) printf(" n=%2d d=%2df=%2d",s->i,s->degree,s->father);printf("\n"); }printf("\n"); }void position(treenode *s,treenode *open,treenode *close,treenode *s1) {int m,n,t,k;treenode *r1;for(m=0;m<3;m++) {for(n=0;n<3;n++) {k=s->a[m][n];if(k==0)break; };if(k==0) break; }if(m+1<=2&&flag==0) {r1=(treenode*)malloc(sizeof(treenode));cpynode(r1,s);t=r1->a[m+1][n];r1->a[m+1][n] = r1->a[m][n];r1->a[m][n]=t;extend(r1,s,s1,open,close); };if(m-1>=0&&flag==0) {r1=(treenode*)malloc(sizeof(treenode));cpynode(r1,s);t=r1->a[m-1][n];r1->a[m-1][n]=r1->a[m][n];r1->a[m][n]=t;extend(r1,s,s1,open,close); };if(n-1>=0 && flag==0) {r1=(treenode*)malloc(sizeof(treenode));cpynode(r1,s);t=r1->a[m][n-1];r1->a[m][n-1]=r1->a[m][n];r1->a[m][n]=t;extend(r1,s,s1,open,close); };if(n+1<=2 && flag==0) {r1=(treenode*)malloc(sizeof(treenode));cpynode(r1,s);t=r1->a[m][n+1];r1->a[m][n+1]=r1->a[m][n];r1->a[m][n]=t;extend(r1,s,s1,open,close); }; }void printstr(treenode *s) {treenode *t;t=s->late;while(t!=NULL) {num++;print(t);t=t->son; }; }void extend(treenode *r1,treenode *s,treenode *s1,treenode *open,treenode *close) {r1->father=s->i;r1->degree=s->degree+1;if(test(r1,s1)!=0) {jscost(r1);if(search(r1,close)==1 && search(r1,open)==1) { xuhao(r1);add1(r1,open);r1->bef=s;count++; }else free(r1); }else {xuhao(r1);jscost(r1);count++;add(r1,close);r1->bef=s;flag=1; } }int search(treenode *s1,treenode *close) { treenode *r,*t;r=s1;t=close->late;while(t!=NULL) {if(r->exp==t->exp) {if(cmpnode(r,t)==1)return 0; };t=t->late; };return 1; }void add(treenode *s,treenode *close) { treenode *r,*t;t=s;r=close;while(r->late!=NULL)r=r->late;r->late=t;t->late=NULL; }void add1(treenode *s,treenode *open){ treenode *t;t=open;s->late=t->late;t->late=s; }void adjust1(treenode *close) {treenode *s,*t;s=close;s->late->bef=NULL;while(s->late!=NULL)s=s->late;s->son=NULL;while(s->bef!=NULL) {t=s->bef;t->son=s;s=s->bef; }; }void jscost(treenode *s) {s->cost=(s->exp)+s->degree; }void sortopen(treenode *open) {treenode *t,*s,*r;int k;r=(treenode*)malloc(sizeof(treenode));t=open->late;while(t!=NULL && t->late!=NULL) {s=t->late;k=t->cost;while(s!=NULL) {if(k > s->cost) {k=s->cost;cpynode(r,t);cpynode(t,s);cpynode(s,r); }s=s->late; }t=t->late; }; }五、实验结果:1.程序截图2.搜索过程请输入八数码的初始状态：（以空格为分隔）2 8 31 0 47 6 5请输入八数码的目标状态：（以空格为分隔）1 2 38 0 47 6 5搜索过程如下：2 8 31 0 4 n= 1 d= 0 f= 07 6 52 0 31 8 4 n= 3 d= 1 f= 17 6 50 2 31 8 4 n= 8 d=2 f= 37 6 51 2 30 8 4 n=10 d= 3 f= 87 6 51 2 38 0 4 n=12 d= 4 f=107 6 55 步,12 个节点Press any key to continue六、实验分析：在进行搜索的过程中，同时记录了扩展新节点的个数。

八数码问题,实验报告八数码实验报告利用人工智能技术解决八数码游戏问题1．八数码游戏问题简介九宫排字问题（又称八数码问题）是人工智能当中有名的难题之一。

问题是在3×3方格盘上，放有八个数码，剩下第九个为空，每一空格其上下左右的数码可移至空格。

问题给定初始位置和目标位置，要求通过一系列的数码移动，将初始位置转化为目标位置。

2．八数码游戏问题的状态空间法表示①建立一个只含有初始节点S0的搜索图G，把S0放入OPEN表中②建立CLOSED表，且置为空表③判断OPEN表是否为空表，若为空，则问题无解，退出④选择OPEN表中的第一个节点，把它从OPEN表移出，并放入CLOSED表中，将此节点记为节点n⑤考察节点n是否为目标节点，若是，则问题有解，成功退出。

问题的解就是沿着n到S0的路径得到。

若不是转⑥⑥扩展节点n生成一组不是n的祖先的后继节点，并将它们记为集合M，将M中的这些节点作为n的后继节点加入图G中⑦对未在G中出现过的（OPEN和CLOSED表中未出现过的）集合M中的节点, 设置一个指向父节点n的指针，并把这些节点放入OPEN表中；对于已在G中出现过的M中的节点，确定是否需要修改指向父节点的指针；对于已在G中出现过并已在closed表中的M中的节点，确定是否需要修改通向他们后继节点的指针。

⑧按某一任意方式或某种策略重排OPEN表中节点的顺序⑨转③3．八数码游戏问题的盲目搜索技术宽度优先搜索：1、定义如果搜索是以接近起始节点的程度依次扩展节点的，那么这种搜索就叫做宽度优先搜索(breadth-first search)。

2、特点这种搜索是逐层进行的；在对下一层的任一节点进行搜索之前，必须搜索完本层的所有节点。

3、宽度优先搜索算法(1) 把起始节点放到OPEN表中(如果该起始节点为一目标节点，则求得一个解答)。

(2) 如果OPEN是个空表，则没有解，失败退出；否则继续。

(3) 把第一个节点(节点n)从OPEN表移出，并把它放入CLOSED 的扩展节点表中。

课案八广度经典八数码难题八数码题目：问题是在3×3方格盘上，放有八个数码，剩下第九个为空，每一空格其上下左右的数码可移至空格。

问题给定初始位置和目标位置，要求通过一系列的数码移动，将初始位置转化为目标位置，下图（图一）为问题的一个状态：算法分析：初始化： 把初始布局存入数据库 data ； 设首指针 closed:=0 ； 尾指针 open:=1 ； repeatclosed 增1 ，取出队列首记录为当前被扩展节点； for r:=1 to 4 do beginif 新空格位置合法 then beginopen 增1 ，并把新布局存入队尾；if 新布局与队列中原有记录重复， then 删除新产生的布局 else if 达到目标 then 输出并退出 end enduntil closedv>=open; {队为空}源程序如下： program zsdf; typebsm=recordt:array[1..3,1..3] of integer;end;tt=array[1..3,1..3] of integer; vara:array[1..1000] of bsm;i,j,k,op,cl:integer;aa,bb:tt;procedure print;beginend;function bijiao1(ttt:tt):boolean; vari,j:integer;beginbijiao1:=true;for i:=1 to 3 dofor j:=1 to 3 doif ttt[i,j]<>bb[i,j]then bijiao1:=false;end;function bijiao2(ttt:tt):boolean;vari,j,k:integer;ab:boolean;beginfor k:=op+1 to cl dobeginab:=true;for i:=1 to 3 dofor j:=1 to 3 doif ttt[i,j]<>a[k].t[i,j]then ab:=false;if ab then dec(cl);{ if bijiao1(a[k].t) then print;}end;end;beginop:=0; cl:=1;assign(input,'d:\sr.in');reset(input);for i:=1 to 3 dobeginfor j:=1 to 3 dofor i:=1 to 3 dobeginfor j:=1 to 3 doread(bb[i,j]);readln;end;if bijiao1(aa) then beginwriteln('no no no!'); halt; end;repeatop:=op+1;until (op>=cl) or (cl>=10000);close(input);end.readln; end;a[cl]:.t=aa; a[cl].。

八数码难题有无解的判断八数码难题有无解的判断我知道什么样的情况有解,什么情况没解.函数f(s)表示s前比s小的数字的数目.例如:|1 3 4||2 8 6||5 7 |表示成:|1 3 4|2 8 6|5 7 X| 则f(7)=6, f(5)=4,f(6)=4,f(8)=4,f(2)=1,f(4)=2,f(3)=1,f(1)=0当f(a8)+f(a7)+……+f(a1)为偶数时才能重排成所以嘛,上面那个有解的.下面我就来证明一下.设任意一种情况:|a1 a2 a3||a4 a5 a6||a7 a8 X | (X表示空格)将之放在一行上: |a1 a2 a3|a4 a5 a6|a7 a8 X |数字的上下移动可以相对于是空格的上下移动.所以我们只要讨论X的移动了:假设函数f(s)表示s前比s小的数字的数目.例如:|1 3 4|2 8 6|5 7 X| 则f(7)=6, f(5)=4, f(8)=4,……对于X在同一行中的移动，f(a8)+f(a7)+……+f(a1)大小不变(*1) 如：|a1 a2 a3|a4 a5 a6|a7 a8 X |=>|a1 a2 a3|a4 a5 a6|a7 X a8| 对于X在列中移动是，我们不妨设X与a6对换(即a6下移一格) 则数列变为|a1 a2 a3|a4 a5 X|a7 a8 a6|,可能引起变化的f(s)只有f(a6),f(a7),f(a8)讨论：有4种情况1) a6<a8<="" p="">f(a8) 减小1f(a7) 减小1f(a6) 不变所以f(a8)+f(a7)+……+f(a1)奇偶性不变.2) a6a8f(a8) 不变f(a7) 减小1f(a6) 增大1所以f(a8)+f(a7)+……+f(a1)奇偶性不变.3) a6>a7, a6>a8f(a8) 不变f(a7) 不变f(a6) 增大2所以f(a8)+f(a7)+……+f(a1)奇偶性不变.3) a6>a7, a6<a8< p="">f(a8) 减小1f(a7) 不变f(a6) 增大1所以f(a8)+f(a7)+……+f(a1)奇偶性不变.这样，再将a3下移一格则|a1 a2 a3|a4 a5 X|a7 a8 a6|=>|a1 a2 X|a4 a5 a3|a7 a8 a6|则同样，对可能变化的f(a3),f(a4),f(a5)讨论，情况一上面完全一样。