三角函数图像与应用

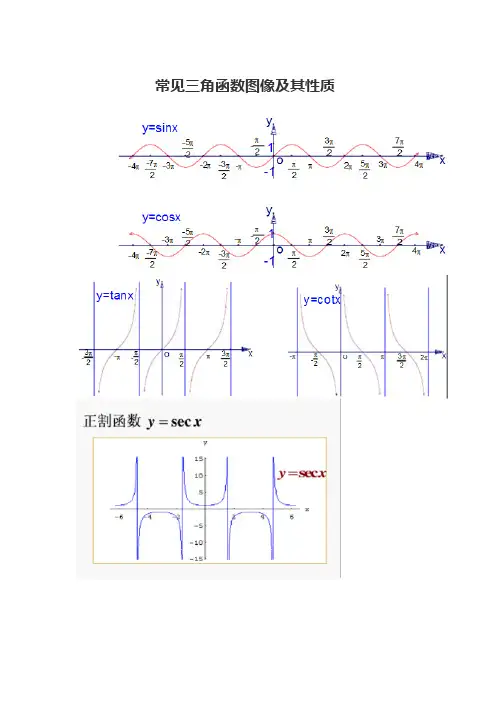
常见三角函数图像及其性质三角函数介绍正弦函数主词条：正弦函数格式：sin（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角对边长度比斜边长度的比值求出，函数值为上述比的比值，也是csc（θ）的倒数函数图像：波形曲线值域：[]1,1-余弦函数主词条：余弦函数格式：cos（θ）作用：在直角三角形中，将大小为（单位为弧度）的角邻边长度比斜边长度的比值求出，函数值为上述比的比值，也是sec（θ）的倒数函数图像：波形曲线值域：[]1,1-正切函数主词条：正切函数格式：tan（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角对边长度比邻边长度的比值求出，函数值为上述比的比值，也是cot（θ）的倒数。

函数图像：上图平面直角坐标系反映值域：()∞-∞，+余切函数主词条：余切函数格式：cot（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角邻边长度比对边长度的比值求出，函数值为上述比的比值，也是tan（θ）的倒数值域：()∞-∞，+正割函数主词条：正割函数格式：sec（θ）作用：在直角三角形中，将斜边长度比大小为θ（单位为弧度）的角邻边长度的比值求出，函数值为上述比的比值，也是cos（θ）的倒数函数图像：上图平面直角坐标系反映值域：(][)∞-1-，1∞，+余割函数主词条：余割函数格式：csc（θ）作用：在直角三角形中，将斜边长度比大小为θ（单位为弧度）的角对边长度的比值求出，函数值为上述比的比值，也是sin（θ）的倒数值域：(][)∞-1-∞，+，1。

高考数学《图像变换在三角函数中的应用》基础知识与典型例题分析在高考中涉及到的三角函数图像变换主要指的是形如()sin y A x ωϕ=+的函数，通过横纵坐标的平移与放缩，得到另一个三角函数解析式的过程。

要求学生熟练掌握函数图像变换，尤其是多次变换时，图像变化与解析式变化之间的对应联系。

一、基础知识：（一）图像变换规律：设函数为()y f x =（所涉及参数均为正数） 1、函数图像的平移变换：（1）()f x a +：()f x 的图像向左平移a 个单位 （2）()f x a −：()f x 的图像向右平移a 个单位 （3）()f x b +：()f x 的图像向上平移b 个单位 （4）()f x b −：()f x 的图像向下平移b 个单位 2、函数图像的放缩变换：（1）()f kx ：()f x 的图像横坐标变为原来的1k（图像表现为横向的伸缩） （2）()kf x ：()f x 的图像纵坐标变为原来的k 倍（图像表现为纵向的伸缩） 3、函数图象的翻折变换： （1）()fx ：()f x 在x 轴正半轴的图像不变，负半轴的图像替换为与正半轴图像关于y 轴对称的图像（2）()f x ：()f x 在x 轴上方的图像不变，x 轴下方的部分沿x 轴向上翻折即可（与原x 轴下方图像关于x 轴对称）（二）图像变换中要注意的几点：1、如何判定是纵坐标变换还是横坐标变换？在寻找到联系后可根据函数的形式了解变换所需要的步骤，其规律如下： ① 若变换发生在“括号”内部，则属于横坐标的变换 ② 若变换发生在“括号”外部，则属于纵坐标的变换例如：()31y f x =+：可判断出属于横坐标的变换：有放缩与平移两个步骤()2y f x =−+：可判断出横纵坐标均需变换，其中横坐标的为对称变换，纵坐标的为平移变换2、解析式变化与图像变换之间存在怎样的对应？由前面总结的规律不难发现： （1）加“常数”⇔ 平移变换（2）添“系数”⇔放缩变换 （3）加“绝对值”⇔翻折变换3、多个步骤的顺序问题：在判断了需要几步变换以及属于横坐标还是纵坐标的变换后，在安排顺序时注意以下原则：① 横坐标的变换与纵坐标的变换互不影响，无先后要求 ② 横坐标的多次变换中，每次变换只有x 发生相应变化 例如：()()21y f x y f x =→=+可有两种方案方案一：先平移（向左平移1个单位），此时()()1f x f x →+。

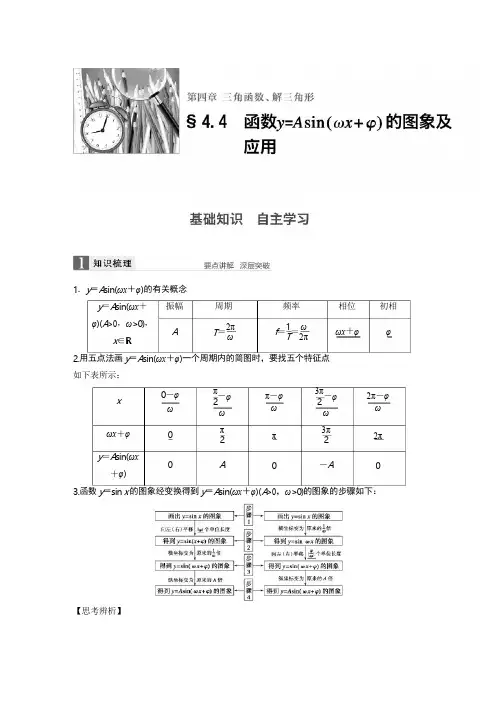
－φ－φ1．y＝A sin(ωx＋φ)的有关概念y＝A sin(ωx＋φ)(A>0，ω>0)，x∈R振幅A周期2πT＝ω频率1ωf＝T＝2π相位ωx＋φ初相φ2.用五点法画y＝A sin(ωx＋φ)一个周期内的简图时，要找五个特征点如下表所示：x0－φωπ2ωπ－φω3π2ω2π－φωωx＋φy＝A sin(ωx＋φ)π2Aπ3π2－A2π0 3.函数y＝sin x的图象经变换得到y＝A sin(ωx＋φ)(A>0，ω>0)的图象的步骤如下：【思考辨析】(2)y ＝sin ⎝x －4⎭的图象是由 y ＝sin ⎝x ＋4⎭的图象向右平移个单位得到的．(√ )1．y ＝2sin ⎝2x －4⎭的振幅、频率和初相分别为2．已知函数 f (x )＝sin ⎝2x ＋6⎭.若 y ＝f (x －φ) (0<φ< )是偶函数，则 φ＝解析 因为 y ＝f (x －φ)＝sin ⎣2(x －φ)＋6⎦＝sin ⎝2x －2φ＋6⎭是偶函数，所以－2φ＋ ＝ ＋k π， k ∈Z ，得 φ＝－ － ，k ∈Z .又 0<φ< ，所以 φ＝ .3．(2015· 湖南改编)将函数 f (x )＝sin 2x 的图象向右平移 φ⎝0＜φ＜2⎭个单位后得到函数 g (x )的]判断下面结论是否正确(请在括号中打“√”或“×”)(1) 利用图象变换作图时“先平移，后伸缩”与“先伸缩，后平移”中平移的长度一致．( × )⎛ π⎫ ⎛ π⎫ π 2(3)由图象求解析式时，振幅 A 的大小是由一个周期内的图象中的最高点的值与最低点的值确定的．( √ )(4)函数 f (x )＝A sin(ωx ＋φ)的图象的两个相邻对称轴间的距离为一个周期．( × )(5)函数 y ＝A cos(ωx ＋φ)的最小正周期为 T ，那么函数图象的两个相邻对称中心之间的距离为T2.( √ )⎛ π⎫1 π答案 2，π，－4．⎛ π⎫ π 2.答案π3⎡ π⎤ ⎛ π⎫ π π 6 2π k π π π6 2 2 3⎛ π⎫π图象，若对满足|f (x 1)－g (x 2)|＝2 的 x 1，x 2，有|x 1－x 2|min ＝3，则 φ＝.答案π6解析 因为 g (x )＝sin [2 x －φ ＝sin(2x －2φ)，所以|f (x 1)－g (x 2)|＝|sin 2x 1－sin(2x 2－2φ)|＝2.因为－1≤sin 2x 1≤1，－1≤sin(2x 2－2φ)≤1，所以 sin 2x 1 和 sin(2x 2－2φ)的值中，一个为 1，另一个为－1，不妨取 sin 2x 1＝1，sin(2x 2－2φ)π π＝－1，则 2x 1＝2k 1π＋2，k 1∈Z,2x 2－2φ＝2k 2π－2，k 2∈Z,2x 1－2x 2＋2φ＝2(k 1－k 2)π＋π，(k 1⎪⎪因为0<φ<，所以0<－φ<，则φ＝.答案y＝10sin⎝8x＋4⎭＋20，x∈[6,14]所以A＝×(30－10)＝10，b＝×(30＋10)＝20，所以ω＝.又×10＋φ＝2π，4所以y＝10sin⎝8x＋4⎭＋20，x∈[6,14]．5．(2014·安徽)若将函数f(x)＝sin(2x＋)的图象向右平移φ个单位，所得图象关于y轴对称，答案3π－k2)∈Z，π得|x1－x2|＝⎪(k1－k2)π＋2－φ⎪.πππ222ππ故当k1－k2＝0时，|x1－x2|min＝2－φ＝3，π64．(教材改编)如图，某地一天从6～14时的温度变化曲线近似满足函数y＝A sin(ωx＋φ)＋b，则这段曲线的函数解析式为．⎛π3π⎫解析从图中可以看出，从6～14时的是函数y＝A sin(ωx＋φ)＋b的半个周期，121212π又2×ω＝14－6，π8π83π解得φ＝，⎛π3π⎫π4则φ的最小正值是．8解析∵函数f(x)＝sin(2x＋)的图象向右平移φ个单位得到g(x)＝sin[2(x－φ)＋]＝sin(2x＋又∵g(x)是偶函数，∴－2φ＝kπ＋(k∈Z)．∴φ＝－－(k∈Z)．当k＝－1时，φ取得最小正值.例1已知函数y＝2sin⎝2x＋3⎭.(3)说明y＝2sin⎝2x＋3⎭的图象可由y＝sin x的图象经过怎样的变换而得到．解(1)y＝2sin⎝2x＋3⎭的振幅A＝2，周期T＝＝π，初相φ＝.(2)令X＝2x＋，则y＝2sin⎝2x＋3⎭＝2sin X.6y＝2sin⎝2x＋3⎭πππ444－2φ)，ππ42kππ283π8题型一函数y＝A sin(ωx＋φ)的图象及变换⎛π⎫(1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；⎛π⎫⎛π⎫2ππ23π⎛π⎫3列表如下：xXy＝sinX⎛π⎫π－π12π212π3π7π123π2－1－25π62π描点画出图象，如图所示：(3)方法一 把 y ＝sin x 的图象上所有的点向左平移 个单位长度，得到 y ＝sin ⎝x ＋3⎭的图象； 再把 y ＝ sin ⎝x ＋3⎭ 的图象上所有点的横坐标缩短到原来的sin ⎝2x ＋3⎭的图象；最后把 y ＝sin ⎝2x ＋3⎭上所有点的纵坐标伸长到原来的 2 倍(横坐标不变 )，即可得到 y ＝2sin ⎝2x ＋3⎭的图象．方法二 将 y ＝sin x 的图象上所有点的横坐标缩短为原来的 倍(纵坐标不变)，得到 y ＝sin 2x再将 y ＝sin 2x 的图象向左平移 个单位长度，得到 y ＝sin ⎣2⎝x ＋6⎭⎦＝sin ⎝2x ＋3⎭的图象；再将 y ＝sin ⎝2x ＋3⎭的图象上所有点的纵坐标伸长为原来的 2 倍(横坐标不变)，即得到 y ＝2sin ⎝2x ＋3⎭的图象．设 z ＝ωx ＋φ，由 z 取 0， ，π， π，2π 来求出相应的 x ，通过列表，计算得出五点坐标，描(1)把函数 y ＝sin(x ＋ )图象上各点的横坐标缩短到原来的 (纵坐标不变)，再将图象向右平移 个单位长度，那么所得图象的一条对称轴方程为(填正确的序号)．①x ＝－ ；②x ＝－ ；③x ＝ ；④x ＝ .(2)设函数 f (x )＝cos ωx ( ω>0)，将 y ＝f (x )的图象向右平移 个单位长度后，所得的图象与原图π ⎛ π⎫ 3⎛ π⎫ 1 2倍 ( 纵坐标不变 ) ，得到 y ＝⎛ π⎫⎛ π⎫⎛ π⎫12的图象；π ⎡ ⎛ π⎫⎤ ⎛ π⎫ 6⎛ π⎫⎛ π⎫思维升华 (1)五点法作简图：用“五点法”作 y ＝A sin(ωx ＋φ)的简图，主要是通过变量代换，π 3 2 2点后得出图象．(2)图象变换：由函数 y ＝sin x 的图象通过变换得到 y ＝A sin(ωx ＋φ)的图象，有两种主要途径：“先平移后伸缩”与“先伸缩后平移”．π 162π3π π π π2 4 8 4π3象重合，则 ω 的最小值等于．答案 (1)① (2)6解析(1)将y＝sin(x＋)图象上各点的横坐标缩短到原来的(纵坐标不变)，得到函数y＝sin(2x＋)；再将图象向右平移个单位长度，得到函数y＝sin[2(x－)＋]＝sin(2x－)，故x 2(2)由题意可知，nT＝(n∈N*)，例2(1)已知函数y＝A sin(ωx＋φ)(A>0，ω>0，|φ|<)的图象上一个最高点的坐标为(2，2)，答案(1)y＝2sin⎝8x＋4⎭(2)f(x)＝2sin(2x＋)⎫解析(1)由题意得A＝2，＝6－2，所以T＝16，ω＝＝.又sin⎝8×2＋φ⎭＝1，所以＋φ＝＋2kπ(k∈Z)．又因为|φ|<，所以φ＝.41234π162πππππ63362π＝－是其图象的一条对称轴方程．π32ππ∴n·ω＝3(n∈N*)，∴ω＝6n(n∈N*)，∴当n＝1时，ω取得最小值6.题型二由图象确定y＝Asin(ωx＋φ)的解析式π2由这个最高点到其右侧相邻最低点间的图象与x轴交于点(6,0)，则此函数的解析式为．(2)函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)的部分图象如图所示，则函数f(x)的解析式为．⎛ππ⎫π3T2ππ⎛ππ4T84πππ224(2)由题图可知A＝2，T7πππ＝－＝，所以T＝π，故ω＝2，因此f(x)＝2sin(2x＋φ)，又⎝12π，－ 2⎭为最小值点， ∴2× π＋φ＝2k π＋ ，k ∈Z ，∴φ＝2k π＋ ，k ∈Z ，∴φ＝ .故 f (x )＝ 2sin(2x ＋ )．则 A ＝ ，b ＝ .(2)求 ω，确定函数的最小正周期 T ，则可得 ω＝ . “最大值点”(即图象的“峰点”)时 ωx ＋φ＝ ；“最小值点”(即图象的“谷点”)时 ωx ＋φ＝ .函数 f (x )＝2sin(ωx ＋φ)⎝ω＞0，－2＜φ＜2⎭的部分图象如图所示，则 φ＝3解析 ∵ ＝ π－ π，⎛ 7 ⎫7 3π12 2π3又|φ|＜π，π3π3思维升华 确定 y ＝A sin(ωx ＋φ)＋b (A ＞0，ω＞0)的步骤和方法：(1)求 A ，b ，确定函数的最大值 M 和最小值 m ，M －m M ＋m2 22πT(3)求 φ，常用的方法有：①代入法：把图象上的一个已知点代入(此时 A ，ω，b 已知)或代入图象与直线 y ＝b 的交点求 解(此时要注意交点在上升区间上还是在下降区间上)．②特殊点法：确定 φ 值时，往往以寻找“最值点”为突破口．具体如下：π23π 2π答案 －T 1152 12 12∴T ＝π.2π又 T ＝ ω (ω＞0)，2π∴ ω ＝π，⎛ ππ⎫.由五点作图法可知当x＝π时，2即2×π＋φ＝，∴φ＝－.y)．若初始位置为P0⎝2，⎭，当秒针从P(注：此时t＝0)正常开始走时，那么点P的纵坐答案y＝sin⎝－30t＋6⎭位是.又函数周期是60(秒)且秒针按顺时针旋转，即T＝⎪ω⎪＝60，所以|ω|＝π⎪2π⎪ππ63030所以y＝sin⎝－30t＋6⎭.例4已知关于x的方程2sin2x－3sin2x＋m－1＝0在⎝2，π⎭上有两个不同的实数根，则m ∴ω＝2.512πωx＋φ＝，5π122π3题型三三角函数图象性质的应用命题点1三角函数模型的应用例3如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置P(x，⎛31⎫2标y与时间t的函数关系式为．⎛ππ⎫解析设点P的纵坐标y与时间t的函数关系式为y＝sin(ωt＋φ)．由题意可得，函数的初相，即ω＝－，⎛ππ⎫命题点2方程根(函数零点问题)⎛π⎫的取值范围是．答案(－2，－1)解析方程2sin2x－3sin2x＋m－1＝0可转化为m＝1－2sin2x＋3sin2x＝cos2x＋3sin2x＝2sin⎝2x＋6⎭，x∈⎝2，π⎭.设2x＋＝t，则t∈⎝6π，6π⎭，6＝sin t，t∈⎝6π，6π⎭，有两个不同的实数根．∴y＝和y＝sin t，t∈⎝6π，6π⎭的图象有两个不同交点，如图：2由图象观察知，的范围为(－1，－)，解析由例4知，的范围是⎣－1，2⎭，∴－2≤m<1，图象的两相邻对称轴间的距离为.(1)求f⎝8⎭的值；(2)求函数y＝f(x)＋f⎝x＋4⎭的最大值及对应的x的值．＝2⎣2＝2sin⎝ωx＋φ－6⎭.⎛π⎫⎛π⎫π⎛713⎫∴题目条件可转化为m⎛713⎫2m⎛713⎫m122故m的取值范围是(－2，－1)．引申探究例4中，“有两个不同的实数根”改成“有实根”，则m的取值范围是．答案[－2,1)m⎡1⎫2∴m的取值范围是[－2,1)．命题点3图象性质综合应用例5已知函数f(x)＝3sin(ωx＋φ)－cos(ωx＋φ)(0＜φ＜π，ω＞0)为偶函数，且函数y＝f(x)π2⎛π⎫⎛π⎫解(1)f(x)＝3sin(ωx＋φ)－cos(ωx＋φ)⎡31⎤sin(ωx＋φ)－2cos(ωx＋φ)⎦⎛π⎫因为f(x)是偶函数，则 φ－ ＝ ＋k π(k ∈Z )，所以 φ＝ ＋k π(k ∈Z )，又因为 0＜φ＜π，所以 φ＝ ，ωx ＋＝2cos ωx .所以 f (x )＝2sin 2⎭⎝因此 f ＝2cos ＝ 2.⎝8⎭x ＋(2)y ＝2cos 2x ＋2cos 2⎣ ⎝ 4⎭⎦2x ＋＝2cos 2x ＋2cos 2⎭⎝－2x ＝2 2sin ⎝4 ⎭2x －＝－2 2sin4⎭⎝令 2x － ＝2k π－ (k ∈Z )，y 有最大值 2 2，所以当 x ＝k π－ (k ∈Z )时，y 有最大值 2 2.设函数 f (x )＝3sin(ωx ＋φ)(ω>0，－ <φ< )的图象关于直线 x ＝ 对称，它的周期①f (x )的图象过点(0， )；π π6 22π32π3⎛ π⎫ 2π π由题意得 ω ＝2· 2，所以 ω＝2.故 f (x )＝2cos 2x .⎛π⎫ π4⎡ ⎛ π⎫⎤⎛ π⎫＝2cos 2x －2sin 2x⎛π ⎫⎛ π⎫ π π4 2π8思维升华 (1)三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型再利用三角函数的有关知识解决问题．(2)方程 根的个数可转化为两个函数图象的交点个数．(3)研究 y ＝A sin(ωx ＋φ)的性质时可将 ωx ＋φ 视 为一个整体，利用换元法和数形结合思想进行解题．π π 2π2 2 3是 π，则下列说法正确的是．(填序号)32②f (x )在[ ， ]上是减函数；③f (x )的一个对称中心是( ，0)；∴f (x )＝3sin(2x ＋φ)，f ( )＝3sin( ＋φ)，则 sin( ＋φ)＝1 或－1.又 φ∈(－ ， )， ＋φ∈( ， π)，∴ ＋φ＝ ⇒φ＝ ，∴f (x )＝3sin(2x ＋ )．①：令 x ＝0⇒f (x )＝ ，正确．②：令 2k π＋ <2x ＋ <2k π＋ ，k ∈Z⇒k π＋ <x <k π＋ ，k ∈Z .令 k ＝0⇒ <x < ，即 f (x )在( ， )上单调递减，而在( ， )上单调递增，错误．③：令 x ＝ ⇒f (x )＝3sin π＝0，正确．④：应平移 个单位长度，错误．典例 (14 分)已知函数 f (x )＝2 3sin( ＋ )·cos( ＋ )－sin(x ＋π)．π 2π12 35π12④将 f (x )的图象向右平移|φ|个单位长度得到函数 y ＝3sin ωx 的图象．答案 ①③2π解析 ∵周期为 π，∴ ω ＝π⇒ω＝2，2π 4π3 34π3π π 4π 5π 112 23 6 64π 3π π3 2 6π 632π π 3π2 6 2π 2π6 3π 2π63π 2π π π6 3 12 65π12π124．三角函数图象与性质的综合问题x π x π2 4 2 4(1)求 f (x )的最小正周期；(2)若将f(x)的图象向右平移个单位长度，得到函数g(x)的图象，求函数g(x)在区间[0，π]上(2)将f(x)解析式中的x换成x－，得g(x)，然后利用整体思想求最值．解(1)f(x)＝23sin(＋)·cos(＋)－sin(x＋π)＝3cos x＋sin x[4分]＝2sin(x＋)，[6分]于是T＝＝2π.[7分](2)由已知得g(x)＝f(x－)＝2sin(x＋)，[9分]∵x∈[0，π]，∴x＋∈[，]，∴sin(x＋)∈[－，1]，[12分]∴g(x)＝2sin(x＋)∈[－1,2]．[13分]a sinα＋b cosα＝a2＋b2sin(α＋φ)(其中tanφ＝)，或a sinα＋b cosα＝a2＋b2cos(α－φ)(其中tanφ＝)，在历年高考中使用频率是相当高的，几乎年年使用到、考查到，应特别加以关注．(sin x·aπ6的最大值和最小值．思维点拨(1)先将f(x)化成y＝A sin(ωx＋φ)的形式再求周期；π6规范解答xπxπ2424π32π1ππ66ππ7π666π162π6故函数g(x)在区间[0，π]上的最大值为2，最小值为－1.[14分]解决三角函数图象与性质的综合问题的一般步骤：第一步：(化简)将f(x)化为a sin x＋b cos x的形式；第二步：(用辅助角公式)构造f(x)＝a2＋b2·b＋cos x·)；a2＋b2a2＋b2第三步：(求性质)利用f(x)＝a2＋b2sin(x＋φ)研究三角函数的性质；第四步：(反思)反思回顾，查看关键点、易错点和答题规范．温馨提醒(1)在第(1)问的解法中，使用辅助角公式baab(2)求g(x)的最值一定要重视定义域，可以结合三角函数图象进行求解．±1．函数y＝cos⎝2x－3⎭的部分图象可能是⎫[方法与技巧]1．五点法作图及图象变换问题(1)五点法作简图要取好五个关键点，注意曲线凸凹方向；(2)图象变换时的伸缩、平移总是针对自变量x而言，而不是看角ωx＋φ的变化．2．由图象确定函数解析式由图象确定y＝A sin(ωx＋φ)时，φ的确定是关键，尽量选择图象的最值点代入；若选零点代入，应根据图象升降找“五点法”作图中第一个零点．3．对称问题函数y＝A sin(ωx＋φ)的图象与x轴的每一个交点均为其对称中心，经过该图象上坐标为(x，A)的点与x轴垂直的每一条直线均为其图象的对称轴，这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离)．[失误与防范]1．由函数y＝sin x的图象经过变换得到y＝A sin(ωx＋φ)的图象，如先伸缩，再平移时，要把x前面的系数提取出来．2．复合形式的三角函数的单调区间的求法．函数y＝A sin(ωx＋φ)(A>0，ω>0)的单调区间的确定，基本思想是把ωx＋φ看做一个整体．若ω<0，要先根据诱导公式进行转化．3．函数y＝A sin(ωx＋φ)在x∈[m，n]上的最值可先求t＝ωx＋φ的范围，再结合图象得出y ＝A sin t的值域．A组专项基础训练(时间：40分钟)⎛π．2x －，∴当2x － ＝0，解析∵y ＝cos 3⎭⎝即 x ＝ 时，函数取得最大值 1，结合图象看，可使函数在 x ＝ 时取得最大值的只有④. 解析 取 K ，L 中点 N ，则 MN ＝ ，因此 A ＝ .由 T ＝2 得 ω＝π.∵函数为偶函数，0<φ<π，∴φ＝ ，∴f (x )＝ cos πx ，3.已知函数 f (x )＝2sin(ωx ＋φ)(ω>0，且|φ|< )的部分图象如图所示，则函数 解析 由函数的图象可得 T ＝ π－ π，又图象过点( π，2)，∴2sin(2× π＋φ)＝2， ∴φ＝－ ＋2k π，k ∈Z ，∵|φ|< ，△KLM 为等腰直角三角形，∠KML ＝90°，KL ＝1，则 f ( )的值为．答案3 ∴f ( )＝ cos ＝ .答案 [k π－ ，k π＋ ]，k ∈Z答案 ④⎛ π⎫ π 3π π6 62．设偶函数 f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，1641212π 2121 1 π 3 62 6 4π2f (x )的单调递增区间是．π 5π12 121 2 54 3 12∴T ＝π，则 ω＝2.5 512 12π3π2∴取 k ＝0，则 φ＝－ ，即得 f (x )＝2sin(2x － )，∴f (x )的单调增区间为 2k π－ ≤2x － ≤2k π＋ ，k ∈Z ，即单调递增区间为[k π－ ，k π＋ ]，k ∈Z .4．已知曲线 f (x )＝sin ωx ＋ 3cos ωx (ω＞0)相邻的两条对称轴之间的距离为 ，且曲线关于点 (x 0,0)中心对称，若 x 0∈⎣0，2⎦，则 x 0＝＝2⎝ sin ωx ＋ ＝2sin ⎝ωx ＋3⎭.∵曲线 f (x )＝2sin ⎝ωx＋3⎭相邻的两条对称轴之间的距离为 ，∴f (x )＝2sin ⎝2x ＋3⎭. 又 x 0∈⎣0，2⎦，∴x 0＝ . 5．函数 f (x )＝sin(2x ＋φ)⎝|φ|＜2⎭的图象向左平移 个单位后所得函数图象的解析式是奇函数，则函数 f (x )在⎣0，2⎦上的最小值为 答案 － 3解析 由函数 f (x )的图象向左平移 个单位得 g (x )＝sin ⎝2x ＋φ＋3⎭的图象，π π3 3π π π2 3 2π 5π12 12π2⎡ π⎤.答案π3解析 f (x )＝sin ωx ＋ 3cos ωx⎛1 2 3 ⎫ 2 cosωx ⎭⎛ π⎫⎛ π⎫ π 22π∴最小正周期 T ＝π＝ ω ，∴ω＝2，⎛ π⎫∵曲线关于点(x 0,0)中心对称；π∴2x 0＋3＝k π(k ∈Z )，k π π∴x 0＝ 2 －6(k ∈Z )，⎡ π⎤ π 3⎛ π⎫ π 6⎡ π⎤．2π ⎛ π⎫ 6因为是奇函数，所以 φ＋ ＝k π，k ∈Z ，又因为|φ|＜ ，所以 φ＝－ ，2x －.所以 f (x )＝sin 3⎭⎝0，，所以 2x － ∈ － ，，又 x ∈⎣ 2⎦ ⎣ 33 ⎦ ∴ω＝ ＝100π.∴I ＝10sin(100πt ＋φ)．，10 ，∵图象过点⎝300⎭∴sin( ＋φ)＝1， ＋φ＝2k π＋ ，k ∈Z ，∴φ＝2k π＋ ，k ∈Z ，又∵0<φ< ，∴φ＝ .100πt ＋，∴I ＝10sin6⎭⎝所以当 x ＝0 时，f (x )取得最小值为－ 3.ω>0,0<φ< ) 的图象如右图所示，则当 t ＝秒时，电流强度是解析由图象知 A ＝10， ＝ － ＝ ， ∴10sin(100π× ＋φ)＝10，当 t ＝ 秒时，I ＝－5 安．7．若函数 f (x )＝sin(ωx ＋φ) (ω>0 且|φ|< )在区间⎣6， 3 ⎦上是单调递减函数，且函数从 1 减小2到－1，则 f ⎝4⎭＝ .答案3π3π π2 3⎛ π⎫⎡ π⎤ π ⎡ π 2π⎤ 326. 电流强度 I ( 安 ) 随时间 t ( 秒 ) 变化的函数I ＝ A sin(ωt ＋ φ)(A >0 ，π 12 100安．答案 －5T4 1 12 300 300 1002πT⎛ 1 ⎫ 1300π π π3 3 2π6π π2 6⎛ π⎫1100π ⎡π 2π⎤⎛π⎫2解析由题意可得，函数的周期为2×⎝3－6⎭＝π，⎛⎫∴f(x)＝sin⎝2x＋6⎭，∴f⎝4⎭＝sin⎝2＋6⎭＝cos＝.8．已知函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜)在一个周期内的图象如图所示．若方程可得φ＝答案或π解析由图象可知y＝m和y＝f(x)图象的两个交点关于直线x＝或x＝π对称，9．(2015·天津)已知函数f(x)＝sin2x－sin2⎝x－6⎭，x∈R.(2)求f(x)在区间⎣－3，4⎦上的最大值和最小值．1－cos⎝2x－3⎭解(1)由已知，有f(x)＝－⎛sin2x－所以f(x)的最小正周期T＝＝π.⎛2ππ⎫2π即ω＝π，∴ω＝2，∴f(x)＝sin(2x＋φ)．πππ由sin⎝2×6＋φ⎭＝1，|φ|<26，⎛π⎫⎛π⎫⎛ππ⎫π362π2f(x)＝m在区间[0，π]上有两个不同的实数x1，x2，则x1＋x2的值为．π433π263π4∴x1＋x2＝3或3π.⎛π⎫(1)求f(x)的最小正周期；⎡ππ⎤⎛π⎫1－cos2x221⎛13＝2⎝2cos2x＋2⎫1sin2x⎭－2cos2x＝311π⎫44cos2x＝2sin⎝2x－6⎭.2π2⎡ππ⎤⎡ππ⎤⎛π⎫1 (2)因为f(x)在区间⎣－3，－6⎦上是减函数，在区间⎣－6，4⎦上是增函数，且f⎝－3⎭＝－4，4 所以 f (x )在区间⎣－3，4⎦上的最大值为 最小值为－ .10．设函数 f (x )＝ 3－ 3sin 2ωx －sin ωx cos ωx (ω>0)，且 y ＝f (x )图象的一个对称中心到最近 的对称轴的距离为 .(2)求 f (x )在区间⎣π， 2 ⎦上的最大值和最小值．解 (1)f (x )＝ 3－ 3sin 2ωx －sin ωx cos ωx＝ － 3× － sin 2ωx ＝ 3 cos 2ωx － sin 2ωx＝－sin ⎝2ωx －3⎭.依题意知 ＝4× ，ω>0，所以 ω＝1.(2)由(1)知 f (x )＝－sin ⎝2x －3⎭.当 π≤x ≤ 时， ≤2x － ≤ .⎛2 故 f (x )在区间⎣π， 2 ⎦上的最大值和最小值分别为 ，－1.11．已知函数 f (x )＝A sin(ωx ＋φ) (A >0，|φ|< ，ω>0)的图象的一部分如图所⎛ π⎫1⎛π⎫3f ⎝－6⎭＝－2，f ⎝4⎭＝，⎡ π π⎤34 ，1 22π 4(1)求 ω 的值； ⎡ 3π⎤231－cos 2ωx 1 2 2 2 12 2⎛π⎫2π π 2ω 4⎛ π⎫3π 5π π 8π 2 3 3 3 所以－ 3 π⎫2 ≤sin ⎝2x －3⎭≤1.所以－1≤f (x )≤ 3.⎡ 3π⎤3 2B 组 专项能力提升(时间：20 分钟)π 2示，则该函数的解析式为 ．答案 f (x )＝2sin ⎝2x ＋6⎭∴1＝2sin(ω·0＋φ)，即 sin φ＝ .∵|φ|< ，∴φ＝ .又∵ π 是函数的一个零点，且是图象递增穿过 x 轴形成的零点，∴ ω＋ ＝2π，∴ω＝2. ∴f (x )＝2sin ⎝2x ＋6⎭. 的交点中，若相邻交点距离的最小值为 ，则 f (x )的最小正周期为．解析 f (x )＝ 3sin ωx ＋cos ωx ＝2sin(ωx ＋ )(ω>0)．由 2sin(ωx ＋ )＝1 得 sin(ωx ＋ )＝ ，∴ωx ＋ ＝2k π＋ 或 ωx ＋ ＝2k π＋ π(k ∈Z )．故 f (x )的最小正周期 T ＝ ＝π.13．已知函数 f (x )＝cos ⎝3x ＋3⎭，其中 x ∈⎣6，m ⎦，若 f (x )的值域是⎣－1，－ 答案 ⎣ 9 ，18⎦⎛ π⎫解析 观察图象可知：A ＝2 且点(0,1)在图象上，1 π π2 2 611 11π π12 12 6⎛ π⎫12．(2014· 天津改编)已知函数 f (x )＝ 3sin ωx ＋cos ωx (ω>0)，x ∈R .在曲线 y ＝f (x )与直线 y ＝1π3答案 ππ6π π 16 6 2π π π 56 6 6 6π π π 5令 k ＝0，得 ωx 1＋6＝6，ωx 2＋6＝6π，2π∴x 1＝0，x 2＝3ω.π 2π π由|x 1－x 2|＝3，得3ω＝3，∴ω＝2.2π2值范围是．⎡2π 5π⎤解析 画出函数的图象．⎛ π⎫ ⎡π ⎤ ⎡ 3⎤ 2 ⎦ ，则 m 的取由 x ∈⎣6，m ⎦，可知 ≤3x ＋ ≤3m ＋ ，且 f ⎝ 9 ⎭＝cos π＝－1，＝－ 要使 f (x )的值域是⎣－1，－2 ⎦ 所以 π≤3m ＋ ≤ π，则 ≤m ≤ ，即 m ∈⎣ 9 ，18⎦.14．已知 f (x )＝sin ⎝ωx ＋3⎭ (ω>0)，f ⎝6⎭＝f ⎝3⎭，且 f (x )在区间⎝6，3⎭上有最小值，无最大值， 答案 146 3 π解析 依题意，x ＝ ＝ 时，y 有最小值，∴sin ⎝4ω＋3⎭＝－1，∴ ω＋ ＝2k π＋ (k ∈Z )，∴ω＝8k ＋ (k ∈Z )，∵f (x )在区间⎝6，3⎭上有最小值，无最大值， 15．已知函数 f (x )＝ 3sin ωx cos ωx ＋cos 2ωx － (ω>0)，其最小正周期为 . (2)将函数 f (x )的图象向右平移 个单位长度，再将图象上各点的横坐标伸长到原来的 2 倍(纵坐标不变)，得到函数 y ＝g (x )的图象，若关于 x 的方程 g (x )＋k ＝0 在区间[0， ]上有且只有一解 (1)f (x )＝ 3sin ωx cos ωx ＋cos 2ωx －⎡π ⎤ 5π π π 6 3 3⎛π⎫ 5π 3 因为 f ⎝6⎭＝cos 6 2⎛2π⎫，⎡ 3⎤ ，π 7 2π 5π3 6 9 18⎡2π 5π⎤⎛ π⎫ ⎛π⎫ ⎛π⎫ ⎛π π⎫则 ω＝.3π π ＋ 2 4⎛π π⎫π π 3π4 3 2143⎛π π⎫π π π 14 ∴3－4<ω，即 ω<12，令 k ＝0，得 ω＝ 3 .1 π2 2(1)求 f (x )的表达式；π8π2个实数解，求实数 k 的取值范围．12＝sin2ωx＋－＝sin(2ωx＋)，所以ω＝2，所以f(x)＝sin(4x＋)．(2)将f(x)的图象向右平移个单位长度后，得到y＝sin(4x－)的图象；再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y＝sin(2x－)的图象，所以g(x)＝sin(2x－)，因为0≤x≤，所以－≤2x－≤，cos2ωx＋11所以g(x)∈[－3又g(x)＋k＝0在区间[0，]上有且只有一个实数解，即函数y＝g(x)与y＝－k在区间[0，]上≤－k<或－k＝1，解得－3<k≤或k＝－1，，]∪{－1}.3π2226π2πππ由题意知f(x)的最小正周期T＝2，T＝2ω＝ω＝2，π6ππ83ππ33πππ2π23332，1]．ππ22有且只有一个交点，由正弦函数的图象可知－32233 22所以实数k的取值范围是(－33 22。

三角函数图像与变换一、引言三角函数是高中数学中的重要内容，它们在数学和物理等领域都有广泛的应用。

本文将从三角函数的图像出发，探讨其与变换的关系，并探讨它们在实际问题中的应用。

二、三角函数的基本图像1. 正弦函数的图像正弦函数是最基本的三角函数之一，它的图像呈现周期性的波动形态。

当自变量为0时，正弦函数的值为0；当自变量为90度（或π/2弧度）时，正弦函数的值为1；当自变量为180度（或π弧度）时，正弦函数的值为0；当自变量为270度（或3π/2弧度）时，正弦函数的值为-1；以此类推，正弦函数的图像在每个周期内都呈现出上升、下降、上升、下降的特点。

2. 余弦函数的图像余弦函数与正弦函数非常相似，它们的图像在形态上只有一个平移。

当自变量为0时，余弦函数的值为1；当自变量为90度（或π/2弧度）时，余弦函数的值为0；当自变量为180度（或π弧度）时，余弦函数的值为-1；当自变量为270度（或3π/2弧度）时，余弦函数的值为0；以此类推，余弦函数的图像也呈现出上升、下降、上升、下降的特点。

3. 正切函数的图像正切函数是另一个重要的三角函数，它的图像呈现出周期性的波动形态。

正切函数的图像在每个周期内都有一个渐进线，即在自变量接近90度（或π/2弧度）和270度（或3π/2弧度）时，函数值趋近于无穷大。

三、三角函数的变换1. 平移变换平移变换是指将函数的图像沿x轴或y轴方向移动一定的距离。

对于正弦函数和余弦函数，平移变换可以通过改变自变量的值来实现。

例如，将正弦函数的自变量增加π/4，可以使函数图像向左平移π/4个单位；将正弦函数的自变量减少π/4，可以使函数图像向右平移π/4个单位。

同样的，对于余弦函数，也可以通过改变自变量的值来实现平移变换。

2. 伸缩变换伸缩变换是指将函数的图像在x轴或y轴方向进行拉伸或压缩。

对于正弦函数和余弦函数，伸缩变换可以通过改变自变量的系数来实现。

例如，将正弦函数的自变量乘以2，可以使函数图像在x轴方向压缩一倍；将正弦函数的自变量除以2，可以使函数图像在x轴方向拉伸一倍。

三角函数的图像和性质三角函数是数学中的重要概念，它们在几何、物理、工程等领域都有广泛的应用。

本文将重点讨论三角函数的图像和性质，并通过具体的例子来说明。

一、正弦函数的图像和性质正弦函数是最基本的三角函数之一，它的图像可以用来描述周期性变化的现象。

正弦函数的图像是一条连续的曲线，它在[-π/2, π/2]区间内单调递增，在[π/2, 3π/2]区间内单调递减。

在整个定义域[-∞, ∞]上，正弦函数的值域为[-1, 1]，且具有奇对称性。

例如，我们考虑正弦函数y = sin(x)在[0, 2π]上的图像。

根据正弦函数的性质，当x=0时，y=0；当x=π/2时，y=1；当x=π时，y=0；当x=3π/2时，y=-1；当x=2π时，y=0。

连接这些点，我们可以得到正弦函数在[0, 2π]上的图像，即一条上下波动的连续曲线。

二、余弦函数的图像和性质余弦函数是另一个基本的三角函数，它也可以用来描述周期性变化的现象。

与正弦函数相比，余弦函数的图像在水平方向上发生了平移，它在[0, 2π]区间内单调递减，在[-π/2, π/2]和[3π/2, 5π/2]区间内单调递增。

在整个定义域[-∞, ∞]上，余弦函数的值域为[-1, 1]，且具有偶对称性。

以余弦函数y = cos(x)在[0, 2π]上的图像为例，当x=0时，y=1；当x=π/2时，y=0；当x=π时，y=-1；当x=3π/2时，y=0；当x=2π时，y=1。

连接这些点，我们可以得到余弦函数在[0, 2π]上的图像，即一条波动的连续曲线。

三、正切函数的图像和性质正切函数是三角函数中的另一个重要概念，它描述了斜率的变化。

正切函数的图像具有周期性，其周期为π。

正切函数在定义域的每个周期内，都有无穷多个渐近线，即x=π/2+kπ，其中k为整数。

正切函数的值域为(-∞, ∞)。

以正切函数y = tan(x)在[-π/2, π/2]上的图像为例，当x=-π/4时，y=-1；当x=0时，y=0；当x=π/4时，y=1。

三角函数的图像与性质及解三角形知识梳理：（1）周期函数的定义对于函数()f x ，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有()()f x T f x +=，那么函数()f x 就叫做周期函数，T 叫做这个函数的周期.（2）最小正周期：若()f x 在所有周期中存在一个最小正数，称它为最小正周期. 当函数sin()(0,0)y A x A ωϕω=+>>表示一个振动量时，A :振幅；12f Tωπ==:频率；2T πω=:周期；x ωϕ+:相位，当0ω=时,ϕ称为初相.sin()(0,0)y A x A ωϕω=+>>和cos()(0,0)y A x A ωϕω=+>>的最小正周期都是2T πω=tan()(0,0)y A x A ωϕω=+>>的最小正周期都是T πω=3、三角函数的最值与值域的常见类型及解题策略函数的sin()y A x k ωϕ=++的最大值是A K +,最小值是A K -最值问题是三角函数中考查频率最高的重点内容之一，是对三角函数概念、图像、性质以及诱导公式、同角三角函数关系、三角公式变换等内容的综合考查，也是与函数的交汇点. （1）sin cos y a x b x =+型引入辅助角公式sin cos )y a x b x x ϕ=+=+，其中tan ba ϕ=，利用三角函数的有界性，有[y ∈.（2）22sin sin cos cos y a x b x x c x =++型22sin sin cos cos sin 2cos 2)y a x b x x c x y A x B x x ϕ=++−−−−→=+=+降次、整理，其中tan B A ϕ=，再利用有界性处理.解三角形知识梳理1．内角和定理（三角形中的边角关系）：①在ABC ∆中，A B C ++=π；sin()A B +=sin C ；cos()A B +=cos C - ②大边对大角，大角对大边 ③在直角三角形中：A+B=C=2π、222,sin sin ,sin 1a b c a b A B C cc=+===，2．正弦定理：在一个三角形中,各边和它的所对角的正弦的比相等.形式一：RCc Bb Aa2sin sin sin ===(解三角形的重要工具)形式二：⎪⎩⎪⎨⎧===CR c B R b AR a sin 2sin 2sin 2 (边角转化的重要工具)形式三：形式四：正弦定理可以用来解两种类型的三角问题：(1)已知两角和任意一边，可以求出其他两边和一角；(2)已知两边和其中一边的对角，可以求出三角形的其他的边和角3.余弦定理：三角形任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍.. 形式一：2222cos a b c bc A =+-2222cos b c a ca B =+- (解三角形的重要工具)2222cos c a b ab C =+-形式二：::sin :sin :sin a b c A B C =sin ,sin ,sin 222a b c A B C RRR ===222cos 2b c aA bc +-=222cos 2a c bB ac+-=余弦定理可解以下两种类型的三角形： （1）已知三边；（2）已知两边及夹角.3、ZZZAXXX 面积公式:222cos 2a b cC ab+-=111sin sin sin 222ABC S ab C bc A ac B∆===。

专题01 三角函数的图象与综合应用【命题规律】三角函数的图象与性质是高考考查的重点和热点内容，主要从以下两个方面进行考查：1、三角函数的图象，涉及图象变换问题以及由图象确定解析式问题，主要以选择题、填空题的形式考查；2、利用三角函数的性质求解三角函数的值、参数、最值、值域、单调区间等，主要以解答题的形式考查.3、三角恒等变换的求值、化简是高考命题的热点，常与三角函数的图象、性质结合在一起综合考查，如果单独命题，多用选择、填空题中呈现，难度较低；如果三角恒等变换作为工具，将其与三角函数及解三角形相结合求解最值、范围问题，多以解答题为主，中等难度．【核心考点目录】核心考点一：齐次化模型 核心考点二：辅助角与最值问题 核心考点三：整体代换与二次函数模型 核心考点四：绝对值与三角函数综合模型 核心考点五：ω的取值与范围问题 核心考点六：三角函数的综合性质【真题回归】1．（2022·全国·高考真题）记函数()sin (0)4f x x b πωω⎛⎫=++> ⎪⎝⎭的最小正周期为T ．若23T ππ<<，且()y f x =的图象关于点3,22π⎛⎫⎪⎝⎭中心对称，则2f π⎛⎫= ⎪⎝⎭（ ） A ．1B ．32C ．52D ．32．（2022·全国·高考真题（理））设函数π()sin 3f x x ω⎛⎫=+ ⎪⎝⎭在区间(0,π)恰有三个极值点、两个零点，则ω的取值范围是（ ）A ．513,36⎫⎡⎪⎢⎣⎭B ．519,36⎡⎫⎪⎢⎣⎭C ．138,63⎛⎤⎥⎝⎦D ．1319,66⎛⎤⎥⎝⎦3．（2022·全国·高考真题）若sin()cos()sin 4παβαβαβ⎛⎫+++=+⎪⎝⎭，则（ ）A ．()tan 1αβ-=B ．()tan 1αβ+=C ．()tan 1αβ-=-D ．()tan 1αβ+=-4．（2022·全国·高考真题（文））将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ，若C 关于y 轴对称，则ω的最小值是（ ）A ．16B ．14C ．13D ．125．（多选题）（2022·全国·高考真题）已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像关于点2π,03⎛⎫⎪⎝⎭中心对称，则（ ）A ．()f x 在区间5π0,12⎛⎫⎪⎝⎭单调递减 B ．()f x 在区间π11π,1212⎛⎫-⎪⎝⎭有两个极值点 C ．直线7π6x =是曲线()y f x =的对称轴D ．直线y x =-是曲线()y f x =的切线 6．（2022·全国·高考真题（理））记函数()()cos (0,0π)f x x ωϕωϕ=+><<的最小正周期为T ，若()f T =，9x π=为()f x 的零点，则ω的最小值为____________． 【方法技巧与总结】1、三角函数图象的变换（1）将sin y x =的图象变换为sin()y A x ωϕ=+(0,0)A ω>>的图象主要有如下两种方法：（2）平移变换函数图象的平移法则是“左加右减、上加下减”，但是左右平移变换只是针对x 作的变换； （3）伸缩变换①沿x 轴伸缩时，横坐标x 伸长(01)ω<<或缩短(1)ω>为原来的1ω（倍）（纵坐标y 不变）；②沿y 轴伸缩时，纵坐标y 伸长(1)A >或缩短(01)A <<为原来的A （倍）（横坐标x 不变）． （4）注意平移前后两个函数的名称是否一致，若不一致，应用诱导公式化为同名函数再平移． 2、三角函数的单调性 （1）三角函数的单调区间sin y x =的单调递增区间是2,2()22k k k ππ⎡⎤π-π+∈⎢⎥⎣⎦Z ，单调递减区间是32,2()22k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z ； cos y x =的单调递增区间是[2,2]()k k k π-ππ∈Z ，单调递减区间是[2,2]()k k k ππ+π∈Z ；tan y x =的单调递增区间是,()22k k k ππ⎛⎫π-π+∈ ⎪⎝⎭Z ．（2）三角函数的单调性有时也要结合具体的函数图象如结合|sin |y x =，sin ||y x =， |cos |y x =，cos ||cos y x x ==的图象进行判断会很快得到正确答案．3、求三角函数最值的基本思路（1）将问题化为sin()y A x B ωϕ=++的形式，结合三角函数的图象和性质求解. （2）将问题化为关于sin x 或cos x 的二次函数的形式，借助二次函数的图象和性质求解. （3）利用导数判断单调性从而求解. 4、对称性及周期性常用结论 （1）对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻两个对称中心之间的距离是半个周期.（2）与三角函数的奇偶性相关的结论若sin()y A x ωϕ=+为偶函数，则有()2k k ϕπ=π+∈Z ；若为奇函数，则有()k k ϕ=π∈Z .若cos()y A x ωϕ=+为偶函数，则有()k k ϕ=π∈Z ；若为奇函数，则有()2k k ϕπ=π+∈Z . 若tan()y A x ωϕ=+为奇函数，则有()k k ϕ=π∈Z ． 5、已知三角函数的单调区间求参数取值范刪的三种方法（1）子集法：求出原函数相应的单调区间，由已知区间是所求某区间的子集，列不等式（组）求解． （2）反子集法：由所给区间求出整体角的范围，由该范围是某相应正弦、余弦函数的某个单调区间的子集，列不等式（组）求解．（3）周期性：由所给区间的两个端点到其相应对称中心的距离不超过14个周期列不等式（组）求解.【核心考点】核心考点一：齐次化模型【规律方法】齐次分式：分子分母的正余弦次数相同，例如：αααα++sin cos sin cos a b c d （一次显型齐次化）或者αααααααααα++⇒+222222sin cos +sin cos sin cos +sin cos sin cos a b c a b c （二次隐型齐次化）这种类型题，分子分母同除以αcos （一次显型）或者α2cos （二次隐型），构造成αtan 的代数式，这个思想在圆锥曲线里面关于斜率问题处理也经常用到.【典型例题】例1．（2022·广东揭阳·高三阶段练习）若tan 2θ=-，则()sin 1sin 24θθπθ-=⎛⎫- ⎪⎝⎭（ ）A ．25B ．25-C ．65D ．65-例2．（2022·江苏省丹阳高级中学高三阶段练习）已知tan 3α=，则3cos cos πcos 2ααα-=⎛⎫+ ⎪⎝⎭（ ）A ．34-B ．34C ．310-D ．310例3．（2022·湖南·高三阶段练习）已知曲线y =()1,4处的切线的倾斜角为2α，则1sin cos π14ααα++=⎛⎫+ ⎪⎝⎭（ ） AB．C ．12D ．1例4．（2022·湖北·襄阳五中高三开学考试）若ππ2θ<<，tan 3θ=-，=（ ） A ．35 B ．54-C ．45-D ．45核心考点二：辅助角与最值问题【规律方法】第一类：一次辅助角:αα±sin cos a b αϕ±)．（其中ϕ=tan b a）第二类：二次辅助角()ωωω±>2sin cos cos ,0a x x b x a bωωω±=2sin cos cos a x x b x ()()ωωωϕϕ±+=±±=sin2cos212(tan )222a b b b x x x a【典型例题】例5．（2022·内蒙古·赤峰二中高三阶段练习（理））已知函数()41sin cos 55f x x x =+，当x β=时，()f x 取得最大值，则cos β=（ ） ABC ．47D ．17例6．（2022·四川省成都市新都一中高三阶段练习（理））若2,43⎡⎤∈⎢⎥⎣⎦x ππ，则函数2()3sin cos =f x x x x 的值域为（ ）A．⎡⎢⎣⎦B．⎡⎢⎣⎦C．D．[0,3+例7．（2022·四川省成都市新都一中高三阶段练习（文））若π0,2x ∈⎡⎤⎢⎥⎣⎦，则函数()23sin cos f x x x x=的值域为（ ）A．⎡⎢⎣⎦B．⎡⎢⎣⎦C．⎡⎣ D．0,3⎡⎣例8．（2022·全国·高三专题练习）函数()222sin f x x x =+，若()()123f x f x ⋅=-，则122x x -的最小值是（ ） A ．23πB ．4πC ．3πD ．6π例9．（2022·浙江省杭州第二中学高三阶段练习）已知关于x 的方程sin cos 2a x b x +=有实数解，则()()2211a b -+-最小值是______．例10．（2022·全国·高三专题练习）函数()44sin sin cos 44xf x x x =+的最小值为___________. 例11．（2022·全国·高三专题练习）已知2251x y -+=，,x y R ∈，则22x y +的最小值为____.核心考点三：整体代换与二次函数模型【规律方法】三角函数和二次函数交汇也是一种常见题型，我们将其分为三类，第一类是最简单的，就是sin x ，cos x 与cos2x 之间的二次函数关系，第二类则有一点隐藏，就是±sin cos x x 与sin cos x x 之间的关系，第三类则是+sin cos a x b x 与sin2x 之间的关系.【典型例题】例12．（2022·全国·高三专题练习）函数3π()sin(2)3cos 2f x x x =+-的最小值为___________． 例13．（2022·全国·高考真题（文））函数cos 22sin y x x =+的最大值为________.例14．（2022·全国·高考真题（理））函数sin cos sin cos y x x x x =++的最大值是_________. 例15．（2022·全国·高三专题练习）已知函数()sin cos 2sin cos 2f x x x x x =+++，则()f x 的最大值为___________.例16．（2022·全国·高三专题练习）若x 是三角形的最小内角，则函数sin cos sin cos y x x x x =+-的最小值是 A．12+B．12-+C ．1 D核心考点四：绝对值与三角函数综合模型 【规律方法】关于=sin y x 和=sin y x ，如图，=sin y x 将=sin y x 图像中x 轴上方部分保留，x 轴下方部分沿着x 轴翻上去后得到，故=sin y x 是最小正周期为π的函数，同理ωφ=+sin()y A x 是最小正周期为πω的函数；=sin y x 是将=sin y x 图像中y 轴右边的部分留下，左边的删除，再将y 轴右边图像作对称至左边，故=sin y x 不是周期函数.我们可以这样来表示：ππππππ⎧∈+⎪=⎨-∈-⎪⎩，，sin ([22])sin sin ((22))x x k k x x x k k ，⎧≥⎪=⎨-<⎪⎩sin (0)sin sin (0)x x x x x 【典型例题】例17．（2022·安徽·铜陵一中高三阶段练习（理））已知函数()sin cos f x x x =+，则下列说法正确的是（ ） A ．()f x 的最小正周期为πB ．()f xC ．()3f x f x π⎛⎫-= ⎪⎝⎭D ．()f x 5,012π⎡⎤-⎢⎥⎣⎦上有解 例18．（2022·全国·高三专题练习）已知()sin |||sin |cos |||cos |=+++f x x x x x ，给出下述四个结论: ①()y f x =是偶函数; ②()y f x =在3,22ππ⎛⎫⎪⎝⎭上为减函数; ③()y f x =在(,2)ππ上为增函数; ④()y f x =的最大值为 其中所有正确结论的编号是（ ）A ．①②④B ．①③④C ．①②③D ．①④例19．（2022·江苏·泗阳县实验高级中学高三阶段练习）已知函数()cos ||2|sin |f x x x =-，以下结论正确的是（ ）A ．π是()f x 的一个周期B ．函数在2π0,3⎡⎤⎢⎥⎣⎦单调递减C ．函数()f x 的值域为[D ．函数()f x 在[2π,2π]-内有6个零点例20．（多选题）（2022·安徽·砀山中学高三阶段练习）已知函数()sin cos 336x x f x π⎛⎫=++ ⎪⎝⎭，则（ ） A ．()f x 的最小正周期为3π B ．()f xC ．()f x 在[5,7]ππ上单调递减D ．()f x 在[4,4]ππ-上有4个零点例21．（2022·湖南省临澧县第一中学高三阶段练习）函数()sin sin cos cos f x x x x x =+++的最大值为______.例22．（2022·全国·高三专题练习）已知函数()sin 2f x x x π⎛⎫=- ⎪⎝⎭，则 ①()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的最小值是1； ②()f x 的最小正周期是2π；③直线()2k x k Z π=∈是()fx 图象的对称轴；④直线2y x π=与()fx 的图象恰有2个公共点.其中说法正确的是________________.例23．（2022·陕西·长安一中高一期末）关于函数()sin sin f x x x =+有下述四个结论： ①()f x 是偶函数；②()f x 在区间()2,π上递增； ③()f x 在[]π,π-上有4个零点； ④()f x 的最大值为2.其中所有正确结论的编号__________.例24．（2022·云南省玉溪第一中学高二期中（文））设函数()cos 2sin f x x x =+，下述四个结论正确结论的编号是__________.①()f x 是偶函数； ②()f x 的最小正周期为π； ③()f x 的最小值为0； ④()f x 在[]0,2π上有3个零点.核心考点五：ω的取值与范围问题【规律方法】1、()sin()f x A x ωϕ=+在()sin()f x A x ωϕ=+区间()a b ，内没有零点⎪⎪⎩⎪⎪⎨⎧+≤+<+<+≤≤-⇒ππϕωπππϕωπk b k k a k T a b 2⎪⎪⎪⎩⎪⎪⎪⎨⎧-+≤-≥≤-⇒ωϕππωϕπk b k a T a b 2 同理，()sin()f x A x ωϕ=+在区间[]a b ，内没有零点 ⎪⎪⎩⎪⎪⎨⎧+<+<+<+<≤-⇒ππϕωπππϕωπk b k k a k T a b 2⎪⎪⎪⎩⎪⎪⎪⎨⎧-+<-><-⇒ωϕππωϕπk b k a T a b 2 2、()sin()f x A x ωϕ=+在区间()a b ，内有3个零点⎪⎩⎪⎨⎧+≤+<++<+≤≤-<⇒ππϕωππππϕωπk b k k a k Ta b T 432(1)(3)(24)T b a k T k a k k b πϕπϕωωπϕπϕωω⎧⎪⎪-+-⎪⇒≤<⎨⎪⎪+<-≤-+-<≤⎪⎩同理()sin()f x A x ωϕ=+在区间[]a b ，内有2个零点⎪⎪⎩⎪⎪⎨⎧+<+≤++≤+<<-≤⇒ππϕωππππϕωπk b k k a k T a b T 32232(2))2(332k TT b k a k b a k πϕππϕωωπϕπϕωω⎧⎪⎪-+-⎪⇒<≤⎨⎪⎪+≤-<-+-≤<⎪⎩ 3、()sin()f x A x ωϕ=+在区间()a b ，内有n 个零点⇒(()(+1)1)(1)22n Tn T b a k k a k n k n b πϕππϕωωπϕπϕωω-+≤-⎧⎪⎪-+-⎪≤<⎨⎪⎪+-+-<≤⎩<⎪同理()sin()f x A x ωϕ=+在区间[]a b ，内有n 个零点(1)(1()()22+1)n T n T b k k a k n k n b a πϕππϕωωπϕπϕωω-+≤-<⎧⎪⎪-+-⎪⇒<≤⎨⎪⎪+-+-≤<⎪⎩4、已知一条对称轴和一个对称中心，由于对称轴和对称中心的水平距离为214n T +，则21(21)42n n T b a πω++==-． 5、已知单调区间(,)a b ，则2T a b -≤.【典型例题】例25．（2022·河南·模拟预测（文））已知函数()()2sin 0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭，3x π=-为()f x 的一个零点，3x π=为()y f x =图象的一条对称轴，且()f x 在,20216ππ⎛⎫⎪⎝⎭内不单调，则ω的最小值为______. 例26．（2022·全国·高三专题练习）若函数()()cos 0f x x ωω=>在区间()2,3ππ内既没有最大值1，也没有最小值1-，则ω的取值范围是___________.例27．（2022·上海·高三专题练习）已知函数cos ,[],y a x x ωππ=+∈-（其中,a ω为常数，且0ω>）有且仅有3个零点，则ω的最小值是_________．例28．（2022·宁夏·平罗中学高三期中（理））已知函数()sin (0)3f x x πωω⎛⎫=+> ⎪⎝⎭，若()f x 在()2ππ，内单调且有一个零点，则ω的最大值是______________．例29．（2022·湖南·永州市第一中学高三阶段练习）若函数()()π2sin 04f x x ωω⎛⎫=+> ⎪⎝⎭在ππ,46⎡⎤-⎢⎥⎣⎦上为增函数，则ω的最大值为________.例30．（2022·全国·高三阶段练习（理））已知函数π()2cos (0)4f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为T ，()f x 的一个极值点为πx=.若π2π33T <<，则ω的最大值是_____.例31．（2022·陕西·蒲城县蒲城中学高三阶段练习（文））将函数()sin2cos 222x x x f x ωωω⎛⎫=-+ ⎪⎝⎭(0ω>)的图象向左平移π3个单位长度,得到曲线C .若C 关于y 轴对称,则ω的最小值是______．例32．（2022·北京师大附中高三阶段练习）记函数()()()cos 0,0f x x ωϕωϕ=+><<π的最小正周期为T ，若()f T =π12x =为()f x 的零点，则ω的最小值为_______． 例33．（2022·云南·高三阶段练习）已知函数()()πsin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭，若π,06⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心，()f x 在区间5π7π,1818⎛⎫⎪⎝⎭上有最大值点无最小值点，且5π7π1818f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，记满足条件的ω的取值集合为M ，则=M ______.例34．（2022·四川成都·模拟预测（理））已知函数()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭，若03f π⎛⎫=⎪⎝⎭，且()f x 在5,312ππ⎛⎫ ⎪⎝⎭上有最大值，没有最小值，则ω的最大值为______． 例35．（2022·全国·高三专题练习（理））设函数()sin()f x x ωϕ=+，其中0ω>．且1(0),0263f f f ππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，则ω的最小值为________．例36．（2022·福建省福州教育学院附属中学高三开学考试）已知()()sin 03f x x πωω⎛⎫=+> ⎪⎝⎭，63f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间,63ππ⎛⎫⎪⎝⎭上有最小值，无最大值，则ω=______.例37．（多选题）（2022·山西·高三阶段练习）已知函数()(0)6f x x πωω⎛⎫=-> ⎪⎝⎭，若()f x 在区间π,π3⎛⎤⎥⎝⎦内没有零点，则ω的值可以是（ ）A ．18B ．12C ．76D ．32核心考点六：三角函数的综合性质 【典型例题】例38．（多选题）（2022·山东德州·高三期中）已知函数()sin()0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭同时满足下列三个条件：②该函数图象的两条对称轴之间的距离的最小值为π； ③该函数图象关于5,03π⎛⎫⎪⎝⎭对称. 那么下列说法正确的是（ ） A ．ϕ的值可唯一确定B ．函数56f x π⎛⎫-⎪⎝⎭是奇函数 C ．当52()6x k k ππ=-∈Z 时，函数()f x 取得最小值 D ．函数()f x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增例39．（多选题）（2022·湖北襄阳·高三期中）函数π()sin(2)3f x x =-的图象向左平移π4个单位长度，得到函数()g x 的图象，则下列结论正确的有（ ） A ．直线5π6x =-是()g x 图象的一条对称轴B ．()g x 在ππ(,)26-上单调递增C ．若()g x 在(0,)α上恰有4个零点，则23π29π(,]1212α∈ D ．()g x 在ππ[,]42上的最大值为12例40．（多选题）（2022·江苏南通·高三期中）已知函数()f x ，()g x 的定义域均为R ，它们的导函数分别为()f x '，()g x '．若()1y f x =+是奇函数，()()cos g x x π'=，()f x 与()g x 图象的交点为()11,x y ，()22,x y ，…，(),m m x y ，则（ ）A ．()f x 的图象关于点()1,0-对称B ．()f x '的图象关于直线1x =对称C ．()g x 的图象关于直线12x =对称D ．()1mi i i x y m =+=∑例41．（多选题）（2022·山东菏泽·高三期中）已知函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示，则下列说法正确的是（ ）．A ．π2f ⎛⎫= ⎪⎝⎭B ．()f x 在区间5π0,12⎛⎫⎪⎝⎭单调递减 C ．()f x 在区间π11π,1212⎛⎫-⎪⎝⎭上有且仅有2个零点 D ．将()f x 的图象向右平移π12个单位长度后，可得到一个奇函数的图象 例42．（多选题）（2022·河北·模拟预测）已知函数π()sin()(0,0π),()04f x x f ωϕωϕ=+><<=，且对任意x ∈R均有π()(),()2f x f f x 在π[0,]2上单调递减，则下列说法正确的有（ ） A ．函数()f x 为偶函数B ．函数()f x 的最小正周期为2πC ．若1()([0,2π])3f x x =∈的根为(1i x i =，2，⋯，)n ，则14πn i i x ==∑ D ．若(2)()f x f x >在(,)m n 上恒成立，则n m -的最大值为π3例43．（多选题）（2022·广东·深圳实验学校光明部高三期中）已知函数π()sin()0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图（1）所示，函数()()1111()cos 0,0,||πg x A x A ωαωα=+>><的部分图象如图（2）所示，下列说法正确的是（ ）A ．函数()y f x =的周期为2πB ．函数()y f x =的图象关于直线1912x π=对称 C ．函数()1y f x =-在区间[0,2]π上有4个零点 D ．将函数()y f x =的图像向左平移23π可使其图像与()y g x =图像重合例44．（多选题）（2022·福建·厦门外国语学校高三期中）将函数()πcos 23f x x ⎛⎫=- ⎪⎝⎭图像上所有的点向右平移π6个单位长度，得到函数()g x 的图像，则下列说法正确的是（ ） A ．()g x 的最小正周期为π B ．()g x 图像的一个对称中心为7π,012⎛⎫⎪⎝⎭C ．()g x 的单调递增区间为()π5ππ,πZ 36k k k ⎡⎤++∈⎢⎥⎣⎦D ．()g x 的图像与函数πsin 26y x ⎛⎫=- ⎪⎝⎭的图像重合例45．（多选题）（2022·黑龙江齐齐哈尔·高三期中）已知()44cossin 22x xf x =+，则下列说法错误的是（ ） A ．函数()f x 的最小正周期为2π B ．函数4f x π⎛⎫- ⎪⎝⎭为奇函数C ．函数()f x 在,63ππ⎛⎫⎪⎝⎭上的值域为5,18⎛⎫⎪⎝⎭D ．函数()34y f x =-在区间[]2,2ππ-上的零点个数为8【新题速递】一、单选题1．（2022·河北·张家口市第一中学高三期中）函数()()πtan 0,02f x x ωϕϕω⎛⎫=+<<> ⎪⎝⎭某相邻两支图象与坐标轴分别交于点π,06A ⎛⎫ ⎪⎝⎭，2π,03B ⎛⎫⎪⎝⎭，则方程()[]πsin 2,0,π3f x x x ⎛⎫=-∈ ⎪⎝⎭所有解的和为（ ） A ．5π12B ．5π6 C ．π2D ．π2．（2022·北京市第十一中学高三阶段练习）已知函数()2π2cos 4f x x ⎛⎫=- ⎪⎝⎭则（ ）A ．()f x 是奇函数B ．函数()f x 的最小正周期为4πC ．曲线()y f x =关于π2x =对称D ．()()12f f >3．（2022·贵州·顶效开发区顶兴学校高三期中（理））已知函数()()sin f x x ωϕ=+（0ω>，π<ϕ），其图象相邻两条对称轴的距离为π2，且对任意x ∈R ，都有()7π12f x f ⎛⎫⎪⎝⎭，则在下列区间中，()f x 为单调递减函数的是（ ） A ．ππ,63⎡⎤-⎢⎥⎣⎦B ．7π0,12⎡⎤⎢⎥⎣⎦C ．π12π,2⎡⎤⎢⎥⎣⎦D ．7π,π12⎡⎤⎢⎥⎣⎦4．（2022·吉林长春·模拟预测）定义域为[]0,π的函数())()1cos cos 02f x x x x ωωωω=-+>，其值域为1,12⎡⎤-⎢⎥⎣⎦，则ω的取值范围是（ ） A ．30,2⎛⎤ ⎥⎝⎦B ．3,32⎡⎤⎢⎥⎣⎦C ．10,3⎛⎤⎥⎝⎦D ．12,33⎡⎤⎢⎥⎣⎦5．（2022·江苏南通·高三期中）已知112tan sin =-αα，则πtan 4α⎛⎫-= ⎪⎝⎭（ ）A ．7-B ．17-C ．19D ．436．（2022·河南·高三阶段练习（理））设函数()sin()(0)5f x x πωω=+>，已知()f x 在[]0,2π有且仅有5个零点，下述四个结论中，正确结论的编号是（ ） ①()f x 在(0,2)π有且仅有3个极大值点②()f x 在(0,2)π有且仅有2个极小值点③()f x 在05π⎛⎫⎪⎝⎭，单调递增④ω的取值范围是1229510⎡⎫⎪⎢⎣⎭， A ．①④B ．②③C ．①②③D ．①③④7．（2022·天津市南开中学滨海生态城学校高三阶段练习）下列关于函数()4cos cos 3f x x x ⎛⎫=- ⎪⎝⎭π的命题，正确的有（ ）个（1）它的最小正周期是π2（2）π,012⎛⎫-⎪⎝⎭是它的一个对称中心 （3）π6x =是它的一条对称轴 （4）它在π0,3⎛⎤⎥⎝⎦上的值域为[]2,3A ．0B ．1C ．2D ．38．（2022·宁夏六盘山高级中学高三期中（理））已知函数()()sin f x x ωϕ=+（其中0,2πωϕ><），()30,88f f x f ππ⎛⎫⎛⎫-=≤ ⎪ ⎪⎝⎭⎝⎭恒成立，且()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调，给出下列命题①()f x 是偶函数；②()304f f π⎛⎫= ⎪⎝⎭；③ω是奇数；④ω的最大值为3；其中正确的命题有（ ）A ．①②③B ．①②④C ．②③④D ．①③④二、多选题9．（2022·重庆八中高三阶段练习）已知函数()()sin 2(0π)f x x ϕϕ=+<<，曲线()y f x =关于点7π,012⎛⎫- ⎪⎝⎭中心对称，则（ ）A ．将该函数向左平移π6个单位得到一个奇函数B ．()f x 在3π7π,46⎛⎫⎪⎝⎭上单调递增 C ．()f x 在π7π,1212⎛⎫-⎪⎝⎭上只有一个极值点 D ．曲线()y f x '=关于直线π6x =对称10．（2022·福建·泉州五中高三期中）已知函数()πsin 23f x x ⎛⎫=- ⎪⎝⎭，则下列结论正确的是（ ）A ．直线7π6x =是()fx 的对称轴B ．点2π,03⎛⎫⎪⎝⎭是()f x 的对称中心 C ．()f x 在区间π22π,3⎡⎤⎢⎥⎣⎦上单调递减D ．()f x 的图象向右平移7π12个单位得cos 2y x =的图象11．（2022·山东青岛·高三期中）已知函数i π()sin 23s n 2cos π66f x x x x x ⎛⎫⎛⎫=++-- ⎪ ⎪⎝⎭⎝⎭，则（ ）A ．()f x 的最大值为2B ．π3x =是()f x 的图象的一条对称轴C ．()f x 在ππ,63⎛⎫-⎪⎝⎭上单调递减 D ．()f x 的图象关于π,06⎛⎫ ⎪⎝⎭对称12．（2022·湖北·荆门市龙泉中学高三阶段练习）设()()sin f x x ωϕ=+（其中ω为正整数，π2<ϕ），且()f x 的一条对称轴为π12x =-；若当0ϕ=时，函数()f x 在ππ,55⎡⎤-⎢⎥⎣⎦单调递增且在ππ,33⎡⎤-⎢⎥⎣⎦不单调，则下列结论正确的是（ ） A ．2ω=B ．()f x 的一个对称中心为5π,06⎛⎫⎪⎝⎭C ．函数()f x 向右平移π12个单位后图象关于y 轴对称 D ．将()f x 的图象的横坐标变为原来的一半，得到()g x 的图象，则()g x 的单调递增区间为()ππ5ππ,Z 242242k k k ⎛⎫-++∈ ⎪⎝⎭三、填空题13．（2022·甘肃·兰州市外国语高级中学高三阶段练习（文））已知函数()()πsin 0,02f x x ωϕωϕ⎛⎫=+><<⎪⎝⎭的相邻对称轴之间的距离为π2，且()f x 图象经过点π,03P ⎛⎫⎪⎝⎭，则下列说法正确的是___________.（写出所有正确的题号）A ．该函数解析式为()πsin 23f x x ⎛⎫=+ ⎪⎝⎭；B ．函数()f x 的一个对称中心为2π,03⎛⎫-⎪⎝⎭C ．函数y =()π5ππ,π2424k k k ⎡⎤-++∈⎢⎥⎣⎦Z D ．将函数()y f x =的图象向右平移(0)b b >个单位，得到函数()g x 的图象，且函数()g x 的图象关于原点对称，则b 的最小值为π3.14．（2022·四川省遂宁市教育局模拟预测（文））正割（Secant ，sec ）是三角函数的一种，正割的数学符号为sec ，出自英文secant ．该符号最早由数学家吉拉德在他的著作《三角学》中所用，正割与余弦互为倒数，即1sec cos x x=．若函数()sec sin f x x x x =⋅-，则下列结论正确的有__ ①函数()f x 的图像关于直线x π=对称；②函数()f x 图像在(),()f ππ处的切线与x 轴平行，且与x 轴的距离为π； ③函数()f x 在区间95,168ππ⎡⎤⎢⎥⎣⎦上单调递增； ④()f x 为奇函数，且()f x 有最大值，无最小值．15．（2022·河南·驻马店市第二高级中学高三阶段练习（理））若1sin cos 2θθ=，则()sin 1sin 2sin cos θθθθ-=+______．16．（2022·吉林·东北师大附中模拟预测）已知函数()sin ||f x x x =，若关于x 的方程()f x m =在4π,2π3⎛⎤- ⎥⎝⎦上有三个不同的实根，则实数m 的取值范围是_________． 四、解答题17．（2022·江西·丰城九中高三开学考试（理））已知函数()2cos 2cos 1f x x x x =-+．(1)求函数()f x 的最小正周期及单调递增区间；(2)若函数()()g x f x k =-在区间π0,2⎡⎤⎢⎥⎣⎦内有两个不同的零点，求实数k 的取值范围．18．（2022·江苏盐城·高三阶段练习）已知函数()22cos 2sin cos sin (04)f x x x x x ωωωωω=+-<<，且_____．从以下①②③三个条件中任选一个，补充在上面条件中，并回答问题：①过点;8π⎛⎝②函数()f x 图象与直线0y 的两个相邻交点之间的距离为;π③函数()f x 图象中相邻的两条对称轴之间的距离为2π．(1)求函数()f x 的单调递增区间；(2)设函数()2cos 23g x x π⎛⎫=-⎪⎝⎭，则是否存在实数m ，使得对于任意1[0,]2x π∈，存在2[0,]2x π∈，()()21m g x f x =-成立?若存在，求实数m的取值范围;若不存在，请说明理由．19．（2022·黑龙江·哈师大附中高三阶段练习）已知函数()4sin cos 3f x x x π⎛⎫=- ⎪⎝⎭(1)求函数()f x 的单调递增区间；(2)若函数()()32g x f x =-在区间（0，π）上恰有2个零点()1212,x x x x <，求()12cos x x -的值．20．（2022·福建省诏安县桥东中学高三期中）已知函数()()()sin 0,0,πf x A x A ωϕωϕ=+>><的部分图象如图所示.(1)求()f x 的解析式及对称中心；(2)先将()f x 的图象横坐标不变，纵坐标缩短到原来的12倍，得到函数()g x 图象，再将()g x 图象右平移π12个单位后得到()h x 的图象，求函数()y h x =在π3π,124x ⎡⎤∈⎢⎥⎣⎦上的单调减区间.21．（2022·青海·西宁市海湖中学高三期中）某同学用“五点法”画函数()sin()0,||2f x A x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在某一个周期内的图象时，列表并填入了部分数据，如下表：()f x 的解析式；(2)将()y f x =图象上所有点向左平移(0)θθ>个单位长度，得到()y g x =的图象．若()y g x =图象的一个对称中心为5,012π⎛⎫⎪⎝⎭，求θ的最小值．22．（2022·北京·北大附中高三阶段练习）已知函数()()sin 0,22f x x ππωϕωϕ⎛⎫=+>-<<⎪⎝⎭的部分图像如下图所示.(1)直接写出()f x 的解析式；(2)若对任意0,3s π⎡⎤∈⎢⎥⎣⎦，存在[]0,t m ∈，满足()()f s f t =-，求实数m 的取值范围.。

三角函数公式及图像
三角函数，又称正弦函数，是一类重要的数学函数，主要用于描述角度之间的关系。

它的公式为：sin θ = y/rcos θ =
x/rtan θ = y/x其中，θ为任意角度，r为角θ的弧长，x和y分
别为角θ在极坐标系中的横坐标和纵坐标。

三角函数的图像是极坐标系中的曲线，如下图所示：图1 三角函数的图像三角函数的应用非常广泛，它可以用来描述各种物理运动的角度。

比如，在电子学中，三角函数可以用来描述电流和电压之间的关系；在机械学中，它可以用来描述物体的运动轨迹；在声学中，它可以用来描述声音的调制和调音，等等。

三角函数也可以用来解决复杂的数学问题，例如：求解多边形的面积、求解椭圆的长短轴、求解圆的面积等。

此外，三角函数还可以用来求解三角形的面积，只要知道三角形的三边长即可求出面积。

除此之外，三角函数还在计算机科学和信号处理等领域有着广泛的应用。

它可以用来描述数字信号的变化趋势，也可以用来做各类图形的绘制和变换，以及处理图像和声音等。

总之，三角函数是一类重要的数学函数，它在物理学、机械学、声学、计算机科学和信号处理等领域的应用都非常广泛，为我们解决复杂的科学问题提供了巨大的帮助。

单位圆定义六个三角函数也可以依据半径为1中心为原点的单位圆来定义。

单位圆定义在实际计算上没有大的价值；实际上对多数角它都依赖于直角三角形。

但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义，而不只是对于在 0 和π/2 弧度之间的角。

它也提供了一个图像，把所有重要的三角函数都包含了。

根据勾股定理，三角函数单位圆的方程是：x^2+y^2=1图像中给出了用弧度度量的一些常见的角。

逆时针方向的度量是正角，而顺时针的度量是负角。

设一个过原点的线，同x轴正半部分得到一个角θ，并与单位圆相交。

这个交点的x和y坐标分别等于 cos θ和 sin θ。

图像中的三角形确保了这个公式；半径等于斜边且长度为1，所以有 sin θ = y/1 和 cos θ = x/1。

单位圆可以被视为是通过改变邻边和对边的长度，但保持斜边等于 1的一种查看无限个三角形的方式。

对于大于 2π或小于等于2π的角度，可直接继续绕单位圆旋转。

在这种方式下，正弦和余弦变成了周期为 2π的周期函数：对于任何角度θ和任何整数k。

周期函数的最小正周期叫做这个函数的“基本周期”。

正弦、余弦、正割或余割的基本周期是全圆，也就是 2π弧度或360°；正切或余切的基本周期是半圆，也就是π弧度或180°。

上面只有正弦和余弦是直接使用单位圆定义的，其他四个三角函数的定义如图所示。

其他四个三角函数的定义在正切函数的图像中，在角kπ附近变化缓慢，而在接近角 (k+ 1/2)π的时候变化迅速。

正切函数的图像在θ = (k + 1/2)π有垂直渐近线。

这是因为在θ从左侧接进 (k + 1/2)π的时候函数接近正无穷，而从右侧接近 (k + 1/2)π的时候函数接近负无穷。

另一方面，所有基本三角函数都可依据中心为O的单位圆来定义，类似于历史上使用的几何定义。

特别三角函数是，对于这个圆的弦AB，这里的θ是对向角的一半，sin θ是AC（半弦），这是印度的阿耶波多介入的定义。