实变函数论课件基数势的定义
- 格式:pdf
- 大小:494.37 KB
- 文档页数:6

实变函数讲义
摘要:
一、实变函数的定义与背景
1.实变函数的定义
2.实变函数的背景与意义
二、实变函数的基本性质
1.连续性
2.可积性
3.可微性
三、实变函数的重要概念
1.实数集
2.实函数的极限
3.实函数的连续
四、实变函数的应用领域
1.数学分析
2.概率论与数理统计
3.工程与物理学
正文:
实变函数是数学中的一个重要分支,它主要研究实数集上的实函数的性质及其应用。
实变函数的定义是指,将实数集上的每一个实数映射到一个实数,满足某种性质的函数。
它的背景与意义在于,它是数学分析的基础,同时在概
率论、数理统计、工程和物理学等领域中都有着广泛的应用。
实变函数具有许多基本性质,包括连续性、可积性和可微性。
连续性是指,当自变量在某一区间内变化时,函数值的变化是连续的。
可积性是指,当自变量在某一区间内变化时,函数值在区间上的积分是有限的。
可微性是指,当自变量在某一区间内变化时,函数值在区间上的微分是存在的。
实变函数中有一些重要的概念,包括实数集、实函数的极限和连续。
实数集是实变函数的基础,它包括了所有的实数。
实函数的极限是指,当自变量趋近某个值时,函数值的变化趋势。
连续是指,当自变量在某一区间内变化时,函数值的变化是连续的。
实变函数的应用领域非常广泛,包括数学分析、概率论与数理统计、工程和物理学等。
在数学分析中,实变函数是分析的基础,它为微积分提供了理论基础。
在概率论与数理统计中,实变函数为概率分布和统计推断提供了理论基础。

《实变函数论》实变函数论是数学的一个重要分支,可以用来分析数学中各种基本实变函数的性质。
它主要是研究如何利用导数、积分、最值和定积分来研究实变函数的性质。
它是求解不可逆微分方程的基础。
它也是研究复变函数性质的基础,把复变函数看作一种特殊的实变函数。
实变函数论包括实值变量函数的微分、积分、最值等,还包括复变量函数的性质。
它是数学分析中的重要分支,与特殊函数论、复变函数论有着密切的关系。
实变函数论中最基础的概念是数量级和极限。
数量级指的是极限的概念,表示随着实变量的变化,函数值的变化程度。
极限是指当实变量接近某个数值时,函数值在某一点处的极限值。
而对极限的深入研究,就是实变函数论的重要内容。
实变函数论几乎可以关注任何一个实变函数的性质,从最基础的极限研究,到有关积分的性质,以及利用实变函数来求解某个特殊的微分方程。
因此,实变函数论的研究对解决各种数学问题都有重要的意义。
实变函数论的重要技术有微分、积分、微分不变性、莱布尼茨定理等等。
它们在极限和积分研究中发挥着重要作用,也是研究复变函数性质的基础。
实变函数论的重要应用在于各种不可逆微分方程的求解。
它可以通过求解它们的极限和积分来解决。
比如,必经微分方程,可以用它的极限和积分来解决;简单自变量微分方程,也可以用它的导数来解决。
由于实变函数论的应用十分广泛,它也与其他学科有着良好的交流和联系。
总之,实变函数论是数学分析中的重要分支,有着重要的研究和实际应用价值,其中涉及到复变函数、微分、积分、最值、极限和定积分等数学基础概念,也与其他学科有着密切的关系。
学习实变函数论不仅有利于研究基础数学,而且可以运用到工程学和其他许多科学中。


实变函数论中的基本概念及性质分析实变函数论是数学分析中的重要内容,主要研究实变函数的基本概念和性质。
实变函数是指定义域和值域都是实数的函数,在实际问题中具有广泛应用。
本文将从实变函数的基本概念、连续性、可导性、极限以及函数的性质等方面对实变函数进行分析。
一、实变函数的基本概念实变函数是数学中最基本的概念之一,它与虚变函数相对应,是指定义域和值域都是实数的函数。
实变函数可以表示为f:D→R,其中D为定义域,R为值域。
实变函数的定义域可以是一个区间、多个区间的并或交,甚至是整个实数集。
实变函数的定义有一些特点,首先是唯一性,同一个定义域和值域的实变函数只能有一个。
其次是有定义性,即每个值域中的元素都有相应的定义域中的元素与之对应。
此外,实变函数还具有有界性、单调性、周期性等多种性质。
二、实变函数的连续性和可导性连续性和可导性是实变函数的重要性质,对于函数的性质和应用具有重要意义。
连续性是指在定义域上函数的变化没有突变,没有间断点。
实变函数在某一点x=c处连续的充分必要条件是:函数在x=c处的极限存在且等于函数在x=c处的值。
如果函数在定义域的每一点处都连续,则称函数在该定义域上连续。
可导性是指函数在某一点处的导数存在。
实变函数f(x)在点x=c处可导的充分必要条件是:函数在点x=c处的两侧导数存在且相等。
如果函数在定义域的每一点处都可导,则称函数在该定义域上可导。
三、实变函数的极限极限是实变函数论中的重要概念,用于描述数列或函数在某一点处的逼近情况。
对于实变函数f(x),当x无限靠近a时,f(x)无限靠近L,我们称L是函数f(x)在点x=a处的极限。
实变函数的极限有一些基本性质,如保号性、四则运算、夹逼准则等。
利用这些性质,我们可以求解实变函数的极限,帮助我们更好地理解和分析函数的行为。
四、实变函数的性质分析实变函数的性质分析是数学分析中的重要内容,可以帮助我们更深入地研究函数的特点和应用。
实变函数的性质有很多,如有界性、单调性、周期性、奇偶性等。





实变函数讲义
摘要:
1.实变函数的定义与性质
2.实变函数的例子
3.实变函数的运算与求导
4.实变函数的应用
正文:
实变函数是数学中的一个重要概念,它是指定义在实数集上的函数。
与复变函数不同,实变函数的自变量和因变量都是实数。
实变函数具有很多重要的性质,这些性质使它在数学分析中有着广泛的应用。
首先,让我们来看一下实变函数的定义与性质。
实变函数是指定义在实数集上的函数,它可以接受实数作为自变量,并输出实数作为因变量。
实变函数具有很多重要的性质,比如连续性、可导性、极限等。
这些性质是实变函数研究的基础,也是实变函数分析的关键。
接下来,我们来看一些实变函数的例子。
最简单的实变函数就是常函数,它的函数图像是一条水平直线。
另外,幂函数、指数函数、对数函数等也是实变函数的例子。
这些函数在实数集上都有定义,并且具有不同的性质。
实变函数的运算与求导是实变函数分析的重要内容。
实变函数的运算包括加法、减法、乘法、除法等。
实变函数的求导则是研究函数在某一点处的变化率。
求导是实变函数分析的重要工具,它可以帮助我们理解函数的性质,并且可以用来求解实际问题。
最后,我们来看一下实变函数的应用。
实变函数在数学中有着广泛的应用,比如在微积分、实分析、概率论等领域都有重要的应用。
实变函数的性质和运算规律可以帮助我们解决实际问题,并且可以用来证明数学定理。
总的来说,实变函数是数学中的一个重要概念,它具有很多重要的性质和运算规律,并且在实际应用中有着广泛的应用。

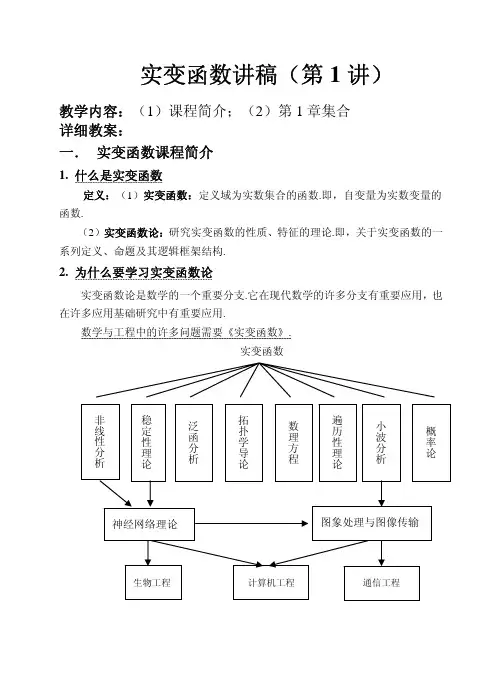
实变函数-集合论(1)实变函数-集合论(1)1. 集合的运算(⼀) 并与交 (i) 满⾜结合律,交换律 (ii) 分配律A ∩(⋃α∈I B α)=⋃α∈I (A ∩B α)A ∪(⋂α∈I B α)=⋂α∈I (A ∪B α)(⼆) 差与补 定义: 设A ,B 是两个集合,称{x :x ∈A ,x ∉B }为A 与B 的差集,记为A ∖B . 当B 是A 的⼦集时,称A ∖B 为集合B 相对于集合A 的补集或余集. 集合B 相对于全集X 的补集简称为B 的补集或余集,记为B c , 即B c =X ∖B . 也记为B c ={x ∈X :x ∉B }.(1) De. Morgan 法则 (i)⋃α∈I A αc =⋂α∈I A c α; (ii) ⋂α∈I A αc =⋃α∈I A c α.(2) 对称差 定义: A 与B 的对称差为A △B =(A ∖B )∪(B ∖A )由定义知A ∪B =(A ∩B )∪(A △B ). 有下列简单事实: (i) A △∅=A ,A △A =∅,A △A c =X ,A △X =A c . (ii) 交换律: A △B =B △A , 结合律: (A △B )△C =A △(B △C ). (iii) 交与对称差满⾜分配律:A ∪(B △C )=(A ∩B )△(A ∩C )(三) 集合列的极限 定义: 设{A k }是⼀个集合列. 若A 1⊃A 2⊃⋯⊃A k ⊃⋯,此时称集合列为递减集合列, 称交集∞⋂k =1A k 为{A k }的极限集, 记为limk →∞A k ; 若A 1⊂A 2⊂⋯⊂A k ⊂⋯,则称{A k }为递增集合列, 称并集∞⋃k =1A k 为{A k }的极限集, 记为\lim\limits_{k\to\infty}A_k . 对于⼀般的集合列, 也可类似于上、下极限的做法来给出上、下限集的概念. 定义: 设\{A_k\}是⼀集合列, 令B_j=\bigcup\limits_{k=j}^\infty A_k显然有B_j\supset B_{j+1}(j=1,2,\cdots). 称\lim\limits_{k\to\infty}B_k=\bigcap\limits_{j=1}^\infty B_j=\bigcap\limits_{j=1}^\infty\bigcup\limits_{k=j}^\infty A_k为\{A_k\}的上极限集(上限集), 记为\overline{\lim\limits_{k\to\infty}}A_k.类似地, 称\bigcup\limits_{j=1}^\infty\bigcap\limits_{k=j}^\infty A_k为\{A_k\}的下极限集(下限集), 记为\varliminf\limits_{k\to\infty}A_k(四) 集合列的直积 定义: 设X,Y 是集合,称⼀切有序元素对(x, y)(其中x\in X,y\in Y )形成的集合为X 与Y 的直积集, 记为X\times Y , 即X\times Y=\{(x,y):x\in X,y\in Y\}()()2. 映射与基数(⼀) 映射 设X,Y为两个⾮空集合. 若\forall x\in X, 均存在唯⼀的y\in Y与之对应, 则称这个对应为映射(变换或函数), 记为f:X\to Y. y称为x在映射f下的像, x称为y的⼀个原像, 记为y=f(x). ⼜可作g:Y\to X, g(y)=x, 其中x由关系y=f(x)确定, 称g为f的逆映射, 记为f^{-1}. 设f:X\to Y, g:Y\to W,则由h(x)=g(f(x))\quad(x\in X)定义的h:X\to W称为g和f的复合映射. 对f:X\to Y以及A\subset X, 记f(A)=\{y\in Y:\ x\in A, y=f(x)\}, 称f(A)为集合A在映射f下的像集(f(\varnothing)=\varnothing). 有下列简单事实: (i) f\left(\bigcup\limits_{\alpha\in I}A_\alpha\right)=\bigcup\limits_{\alpha\in I}f(A_\alpha); (ii) f\left(\bigcap\limits_{\alpha\in I}A_\alpha\right)\subset\bigcap\limits_{\alpha\in I}f(A_\alpha). 设f:X\to Y以及B\subset Y, 记f^{-1}(B)=\{x\in X:\ f(x)\in B\}, 称f^{-1}(B)为集合B关于f的原像集. 有下列简单事实: (i) 若B_1\subset B_2, 则f^{-1}(B_1)\subset f^{-1}(B_2)\quad(A\subset Y); (ii) f^{-1}\left(\bigcup\limits_{\alpha\in I}B_\alpha\right)=\bigcup\limits_{\alpha\in I}f^{-1}(B_\alpha)\quad(B_\alpha\subset Y,\alpha\in I); (iii) f^{-1}\left(\bigcap\limits_{\alpha\in I}B_\alpha\right)=\bigcap\limits_{\alpha\in I}f^{-1}(B_\alpha)\quad(B_\alpha\subset Y,\alpha\in I); (iv) f^{-1}(B^c)=(f^{-1}(B))^c\quad(B\subset Y). 若对每⼀个y\in Y, 均有x\in X, 使得y=f(x), 则称f为从X到Y的满射. 若当x_1,x_2\in X且x_1\neq x_2时, 有f(x_1)\neq f(x_2), 即X中不同元有不同的像,称f是从X到Y的⼀个单射. 若f既是单射⼜是满射, 则称f为X到Y上的⼀⼀映射.(⼆) 特征函数 定义: 对于X中的⼦集A, 作\chi_A(x)=\begin{cases}1,&x\in A,\\0,&x\in X\setminus A,\end{cases}且称\chi_A:X\to\mathbb{R}是定义在X上的A的特征函数. 特征函数可以认为就是集合, 即特征函数和集合是同构的. 集合问题都可以变为特征函数问题, 如A\neq B即\chi_A\neq\chi_B, A\subsetB即\chi_A(x)\le \chi_B(x). 有下列简单事实: (i) \chi_{A\cup B}(x)=\chi_A(x)+\chi_B(x)-\chi_{A\cap B}(x); (ii) \chi_{A\cap B}(x)=\chi_A(x)\cdot\chi_B(x); (iii) \chi_{A\setminus B}(x)=\chi_A(x)[1-\chi_B(x)]; (iv) \chi_{A\triangle B}(x)=\left|\chi_A(x)-\chi_B(x)\right|.(三) 幂集 设X是⼀个⾮空集合, 由X的⼀切⼦集为元素形成的集合称为X的幂集, 记为\mathscr{P}(X). 集合势(即集合的元素个数)有限假设为n, \mathscr{P}(X)元素个数为2^n.(四) 基数(集合的元素个数) 定义: 设有集合A与B. 若存在⼀个从A到B上的⼀⼀映射, 则称A与B对等, 记为A\sim B. 显然, 对等关系有如下的基本性质: (i) ⾃反性: A\sim A (ii) 对称性: 若A\sim B, 则B\sim A (iii) 传递性: 若A\sim B, B\sim C, 则A\sim CCantor-Bernstein定理 引理(集合在映射下的分解): 若有f:X\to Y,g:Y\to X, 则存在分解X=A\cup A^{\sim},\quad Y=B\cup B^{\sim}其中f(A)=B,g(B^{\sim})=A^{\sim},A\cap A^{\sim}=\varnothing以及B\cap B^{\sim}=\varnothing. : 若集合X与Y的某个真⼦集对等, Y与X某个真⼦集对等, 则X\sim Y. 证明: 由题设知存在单射f:X\to Y与单射g:Y\to X, 由映射分解定理知X=A\cup A^{\sim},\quad Y=B\cup B^{\sim},\quad f(A)=B,\quad g(B^{\sim})=A^{\sim}.注意到f:A\to B以及g^{-1}:A^{\sim}\to B^{\sim}是⼀⼀映射, 因此可作X到Y上的⼀⼀映射F:F(x)=\begin{cases}f(x),&x\in A\\g^{-1}(x),&x\in A^{\sim}\end{cases}这说明X\sim Y. 现在我们描述集合的基数(或势)的概念. 设A,B是两个集合, 如果A\sim B, 那么我们就说A与B的基数(cardinal number)或势是相同的, 记为\overline{\overline{A}}=\overline{\overline{B}}.⾃然数\mathbb{N}的基数,可列集 记⾃然数集\mathbb{N}的基数为\aleph_0(读作阿列夫(Aleph)零). 若集合A的基数为\aleph_0, 则A叫做可列集. ,这是由于\mathbb{N}=\{1,2,\cdots,n,\cdots\}, ⽽A\sim\mathbb{N}, 故可将A中元素按⼀⼀对应关系以⾃然数次序排列起来,有:A=\{a_1,a_2,\cdots,a_n,\cdots\}. 定理1: 任⼀⽆限集E必包含⼀个可列⼦集. 证明任取E中⼀元, 记为a_1; 再从E\setminus\{a_1\}中取⼀元, 记为a_2,\cdots,设已选出a_1,a_2,\cdots,a_n. 因为E为⽆限集, 所以E\setminus\{a_1,a_2,\cdots,a_n\}\neq\varnothing于是⼜从E\setminus\{a_1,a_2,\cdots,a_n\}中再选⼀元, 记为a_{n+1}. 这样, 我们就得到⼀个集合\{a_1,a_2,\cdots,a_n,a_{n+1},\cdots\}.这是⼀个可列集且为E的⼦集. 定理2: 若A_n(n=1,2,\cdots)为可列集, 则并集A=\bigcup\limits_{n=1}^\infty A_n也是可列集. 证明只需讨论A_i\cap A_j=\varnothing的情况. 设A_1=\{a_{11},a_{12},\cdots,a_{1j},\cdots\},A_2=\{a_{21},a_{22},\cdots,a_{2j},\cdots\},\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdotsA_i=\{a_{i1},a_{i2},\cdots,a_{ij},\cdots\},\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots则A=\{a_{11},a_{21},a_{12},a_{31},a_{22},a_{13},\cdots,a_{ij},\cdots\}(规律为a_{11}排第⼀, 当i+j\gt2时,a_{ij}排第n位, n=j+\sum\limits_{k=1}^{i+j-2}k)为可列集.推论: 有理数集\mathbb{Q}是可列集. 定理3: 设A是⽆限集且其基数为\alpha. 若B是⾄多可列集, 则A\cup B的基数仍为\alpha. 证明不妨设B=\{b_1,b_2,\cdots\},A\cap B=\varnothing, 且A=A_1\cup A_2,\quad A_1=\{a_1,a_2,\cdots\}.作映射f如下:f(a_i)=a_{2i},\quad a_i\in A_1;\quad f(b_i)=a_{2i-1},\quad b_i\in B; 显然, f是A\cup B到A上的⼀⼀映射. 定理4: 集合A作为⽆限集的充分必要条件是A与某某真⼦集对等.\mathbb{R}的基数,不可数集 通过⼀⼀映射f(x)=\frac{x+1}{2}可知, [-1,1]与[0,1]对等. 因此, 要研究实数集\mathbb{R}的基数, 只需讨论[0,1]的基数即可. 定理5: [0,1]=\{x:0\le x\le 1\}不是可数集. 称(0,1]的基数为连续基数, 记为c(或\aleph_1). 易知\overline{\overline{R}}=c. 定理6: 设有集合列\{A_k\}. 若每个A_k的基数都是连续基数, 则其并集\bigcup\limits_{k=1}^\infty A_k的基数是连续基数. 定理7(⽆最⼤基数定理): 若A是⾮空集合, 则A与其幂集\mathscr{P}(A)不对等.Loading [MathJax]/jax/element/mml/optable/GeneralPunctuation.js。
实变函数笔记(1)——集合与基数 实变函数这门课应该是我这学期最为困难的⼀门课,因此更需要加把劲去学习。
这门课⼀开始是从定积分的定义出发的,我们知道求曲边梯形⾯积⼀共分为4步:(1)划分区间;(2)对每个⼩区间[x i−1,x i]上选定⼀点ξi计算f(ξi);(3)对每个区间上的⼩矩形⾯积求和;(4)令最⼤的⼩区间长度趋向于0,如果求和存在极限,那么记为定积分lim λ→0n∑i=1f(ξi)△x i=∫b a f(x)dx,其中λ=max(|x i−x i−1|)。
接着在数学分析中我们已经知道连续函数必然可积,除此之外,还有什么类型的函数可以求定积分呢?考虑下⾯的函数f(x)=0x∈Q x x∉Q 显然⽆论△x i多么⼩均可以找到ξi∈Q或ξi∉Q,因此定积分∫b a f(x)dx不存在。
基于以上事实,我们需要将现有的黎曼积分推⼴,之后我们会看到,当对y进⾏划分时,如果x轴上的测度存在,那么我们可以定义Lebesgue积分(L)∫b a f(x)dx 这门课程的⼀个⼤⽬标是证明这个定理:如果函数f(x)黎曼可积,那么它必然Lebesgue可积,并且两者相等,反之不然。
为了证明该定理,我们引⼊了⼀系列新的概念,⽐如建⽴了测度,它是长度、⾯积和体积的推⼴。
此外还将连续函数推⼴为可测函数,利⽤可测集代替开区间,可以断⾔的是,可测集⼏乎是开区间,可测函数⼏乎是连续函数。
让我们从集合开始,它是建⽴测度的基础。
⼀、集合的基本运算 集合的基本运算在离散数学课程已经提到过,这⾥只需要重新回忆起即可。
Def1 (⼦集、补集、集合的相等)⼦集是说对于两个集合A和B,如果集合A的所有元素都是集合B的元素,那么称A是B的⼦集。
补集是说给定全集U及它的某个⼦集A,由所有x∈U但x∉A的元素组成集合称为A的补集,称为¯A或者A C集合的相等是指对于两个集合A和B,如果A⊂B且B⊂A,那么有A=B 对于集合的交集、并集,有如下的公式以及De Morgan法则Thm2 (集合的交并补公式)(1) A⋂(B⋃C)=(A⋂B)⋃(A⋂C)(2) (A⋂B)⋃C=(A⋃C)⋂(B⋃C)Thm3 (De Morgan法则)设{A i}为集合列,那么成⽴如下并集和交集规律(1) (⋃n i=1A i)C=⋂n i=1(A i)C(2) (⋂n i=1A i)C=⋃n i=1(A i)C 接下来需要对集合引⼊极限的概念,我们称之为上极限集和下极限集。
目的:掌握势的定义,熟悉势的性质, 了解势的比较。
重点与难点:势的定义及比较。
现实生活中,当我们谈到一组对象时,很自然的会涉及到这一组对象的个数。
集合论也是这样.假如我们不考虑某个集合中元素的具体特性时,该集合含多少个元素则是一个最基本的概念,比如10个人组成的集合与十块砖头组成的集合,虽然特征不同,但作为集合,它们含相同个数的元素,十块砖头与九块砖头虽然有相同的属性,但其元素个数不同,而是两个不同的集合。
由此可见,集合所含元素的个数也是集合的一个重要的特征。
一.势的定义问题1:回忆有限集是如何计数的?问题2:有限集的计数方法如何移植到无限 集情形?心里默数着1,拿起第二粒石子时,心里默数着2,拿起最后一粒石子时,我们心里默数的最后一个数字就是石子的个数。
在这个过程中,我们不知不觉间将每粒石子都编了号,第一粒石子就是一号,不妨记作 ,第二粒石子就是二号,不妨记作 ,如果有n个石子,则最后一粒石子就是第n号,记作 ,于是这堆石子 ,...2e 1e ne设想有一堆石子,我们要知道它有多少个,当我们拿起第一粒石子时,可记作 。
这个过程实际上建立了石子与自然数1到n之间的一个一一对应关系。
如果我们想知道两堆石子是否有相同个数,我们其实不必将这两堆石子的个数一一数出来,而只需每次各从两堆石子中拿一粒,只要最后各剩下一粒石子,则它们的个数就是一样的,否则就不同。
这说明,我们想知道两个集合是否有相同}...,,{21n e e e个数,我们其实不必将这两堆石子的个数一一数出来,而只需每次各从两堆石子中拿一粒,只要最后各剩下一粒石子,则它们的个数就是一样的,否则就不同。
这说明,我们想知道两个集合是否有相同数量的元素,只需看能否在这两个集合之间建立一种一一对应关系,只要能建立这种关系,我们就有理由认为,它们有相同的数量,这种方法对无穷集也适用。
8映射1 , . , , ,: ,fA B A f A x B y f A B f A B A B →−−→定义设是两个集合,非空集若依照规则对于中的每个元,在中都有唯一确定的元与之对应就称是到的映射记作或9{}{} , ()., ()| .()| , ().x y x f f x A f f x x A f f x x E E f f E ∈∈而与对应的元称为(在映射下)的象记作集合称为映射的定义域集合称为映射的值域集合称为在映射下)的象集记作102 : () , .i.e.,,,().()(), .i.e.,,,()(f f A B f A B f y B x A f x y A B y f A x A f x y f x y A f x f →∀∈∈=−−→∈∈=∀∈=定义若映射的值域恰等于就说是满射的存在使得若映射使每个仅有唯一的满足就说是单射的若1111),. : , , (),: .f y x y f A B f A B f A B A B --=→−−→−−→则若映射既是满射的又是单射的就称是到的一一映射“一一映射”有时还说成“一一对应”记作或111 , (), () ( () , , , .f A B y B x A f x yg y x f x y g B A g f f -∈∈===设是到的一一映射则对每个有唯一使定义当时)则是到的一一映射我们称是的逆映射记作注:称与A 对等的集合为与A 有相同的势(基数), 记作势是对有限集元素个数概念的推广.ABA ~ΦΦ~131 ~ ~, ~ ~, ~, ~. i A A ii A B B A iii A B B C A C 命题对等关系有如下性质:(); (反身性)()若则 ; (对称性)()若则 (传递性)1412121212n 1n 1n 1n 12 ,,,, ,,,,, . ~(1,2,), ; ~ (1,2,).;~ ,n n n n mmn n n n A A A B B B A B n A A B B A B m A B ==∞∞==== 命题设是两两无交的一列集是两两无交的一列集若则~, :. : , ()(),1,2,.n n n n n n n A B f A B f x A f x f x n →∈== 证明故存在一一映射 作映射对每个令 例1 作对应关系则 是 与 之间的一一对应。
Z N ~⎩⎨⎧=-→+=→,2,1,012,2,12:n n n n n n φφN Z{}{}.~ ,,2,,4,2 ,,,,2,1 2 Ne N n Ne n N 则设例 ==.),( 2)( 的一一映射到是显然定义证明Ne N f N n n n f ∈= 12 例、揭示出了一个极其重要的事实,就是无限集是有可能与它的真子集对等的,我们还将证明任何一个无限集必然与它的一个真子集对等,这对于有限集来说,显然是永远办不到的。
~~~N N N Z奇数偶数结论:173 (01)~[01].例,,.,5,4,3 ,101)101( ,1)101( ,0)101( , .,101,,101,101,1,0,,101,101,101,101,101 2222432 ====⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧=--n f f f f B A B A n n n n 使映射的到作设证明].1,0[~)1,0( 2 .\]1,0[~\)10( ,\]1,0[\)1,0( . 11便知由命题,故又显然B A B A B A f=−→−-18(01)~().a b 例,, ()() .f x a b a x =+-证明定义 (01)~.R 例, ()tan() .2f x x ππ=-证明定义(0,1)~[0,1]~(,)~(,)~,a b a b -∞+∞<>结论:例4 N与R 1不对等,即 。
若不然,存在 与 的一个一一对应 , 将与N中n对应的元素 记为 ,则 上至少有一个单位长度的区间不含 ,不妨设此间 分为三等分,则 中至少不含 ,==≠1R N )(n φ1R ]1,0[],1,0[1将=I ]1,31[],31,0[φn r 1r 1R N 2r 以 表示这个区间,将 三等分,其左、右两个区间中至少有一个区间不含 ,记为 ,依此类推,可得一串闭区间 ,满足:(1) ,且 的长度趋 于0(2) 。
2I 2I 3r 3I n I ⊃⊃⊃321I I I n I ,3,2,1,=∈n I r n n 由闭区间套定理知 ,但对任意φ≠∞=n n I 1n n m I r m ∞=∈1, ,换言之,n n I ∞=1不在R 1中,这是不可能的。
这一矛盾说明, N与R 1不可能对等。
例4 说明,两个无限集的确可能有不同的势,既然势可以不同,如何对其进行比较呢?下面的定义给出了比较的方法。
2势的比较定义4 假设A、B是两个集合,若A与B 的某个真子集B*对等,但不与B对等,则说 A的势小于B的势,记作 ,或说B的势 大于A的势,记作 。
B A <B A >定义3 假设A与B对等,则说A的势等于B的势, 记作A B=;则称若B A B A =,~)112)~,A B B A B A B B A ⊂≤若则称;相当于:到有一个单射,也相当于到有一个满射3),A B A B A BA B ≤≠<若且,则称注:不能用与的一个真子集对等描述.A B A B ≤⇔命题与的某个子集对等 .A B A B =⇔ 命题从合理性方面讲,任何两个集合A和B 的势都应该是可以比较大小的,即下面三种 情况必有且仅有一种情况出现:(i) ;(ii) ;(iii) 。
B A =B A >BA < 遗憾的是,至今尚无法证明或否认这是真的。
Zermelo给集合论加上了一条公理,即Zermelo选择公理,依据这条公理便可证明(i)、(ii)、(iii)有且仅且一种情形发生。
26., , Bernstein 1 00对等与则对等的子集与且对等的子集与设定理)(定理B A A A B B B A .~ .~ 01100110A B g A B B A f B A gf--−→−−→−使知可找到一个由使知可找到一个由证明ABA fgB 27ABA 1A 2A 3A 1B 2B 3B ff fgggB ,)( \ 1110B A f A A A ==令,)( )( 2221B A f A B g ==.,)( )(3332 B A f A B g ==280210101212121223230123123123123 () (),\, .,, , ,, ,g B A A g B A A A A A A A A f B B B B f A A A A A A A A A A A A A A f B B B ==⊂=由知而故、无交从而、在下的象集、无交从而、在下的象集、无交由、均包含于知与、均无交故、、两两无交从而、、在下的象集、、两两无交这样一直递推下去123123 , .A A AB B B 便知、、,两两无交并且、、,也两两无交29111111(1,2,), . (1)f fn n n n n n A B n A B ∞∞--==−−→=−−→ 显然从而1111112(1,2,), . (2)g gn n n n n n B A n B A ∞∞+--==−−→=−−→ 另一方面从而0110111211111, 2\\\ \\. (3)gg n n nn n n g n n n n B A B B A A A A A A B B -∞∞∞-===∞∞-==−−→−−→=−−→ 由于结合()便知于是13 A ~B由()及()便知30.~~ ,~ , 1 C B A C A C B A 则若系⊃⊃.~~ .~ 1 . , .)( .)( ),( ,. ~ 1111C B A C B C B C B C B f C B C B f B f B A B C A f C A ff从而便知由定理等对的一个子集当然与又对等的一个子集与即故而使,故可找到证明⊂⊂−→−⊂−→−--.4 3 ,1 ,. 1 Bernstein 所述的结论立即推出例可从例根据系例如工具是证明集合对等的有力定理及系,,.A B B C A C<<<定理若则..,)(~. )( ,,.111111不成立再证于是从而使及故存在使及故存在证明CACACBgAC BgBCCBCgC BBBABfBAg gf=≤⊂⊂→⊂→<⊂→<---. ...2 ,,CACAC BB CBCBACA< =<><<=所以不成立可见相矛盾这与题设不再成立知:从而由定理知则由假若31。