- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
(0) (1) (1) G1( 0 ) 与 G2(1) ~ G5(1) 之间以及 G2 与 G2 ~ G5 之间的两两
距离,并选用其最小者。
G1(1)
(1) G2
G3(1)
(1) G4
G5(1)
G1(1)
(1) G2
0
6 5 8
0
13 6 8
G3(1)
(1) G4
0
7
0
4
G5(1)
14
11
0
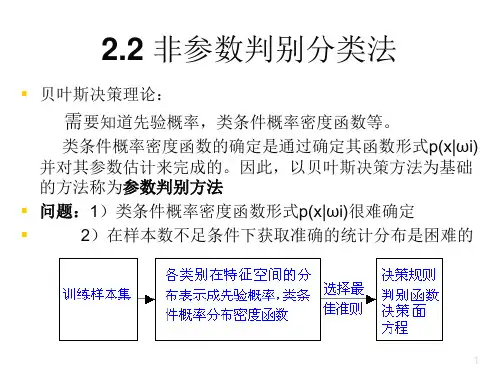
系统聚类算法: 第一步:设初始模式样本共有 N 个,每个样本自
(0) (0) (0) 成一类,即建立 N 类, G1 , G2 , , G N 。
计算各类之间的距离(初始时即为各样本间 的距离),得到一个 N×N 维的距离矩阵 D(0)。这里,标号(0)表示聚类开始运算前的 状态。 第二步:假设前一步聚类运算中已求得距离矩阵 D(n),n 为逐次聚类合并的次数,则求 D(n)中的最小元素。如果它是 Gi(n)和 Gj(n)两
特例:当 m=1 时, D1 ( x i , x j ) |x ik x jk | ,亦
k
称为街坊距离。 角度相似性函数
xTz 表达式: S( x, z) x z ,它表示模式向量
x 和 z 之间夹角的余弦,也称为 x 的单位向量与 z 的单位向量之间的点积。 特例:当特征的取值仅为(0, 1)两个值时,夹 角余弦度量具有特别的含义,即当模式的第 i 个分量为 1 时,认为该模式具有第 i 个特征; 当模式的第 i 个分量为 0 时,认为该模式无此 特征。这时,xTz 的值就等于 x 和 z 这两个向量 共同具有的特征数目。同时,
一般化的明氏距离 模式样本向量 xi 和 xj 之间的明氏距离表示为:
D m ( x i , x j ) ( x ik x jk ) m k
1/ m
其中 xik 和 xjk 分别表示 xi 和 xj 的第 k 各分量。 显然,当 m=2 时,明氏距离即为欧氏距离。
(0) G2 (0) G2
G3( 0 )
(0) G4
G5( 0 )
(0) G6
0
3 15 6
0
6 5 8
G3( 0 )
(0) G4
0
13 6 8
0
7
G5( 0 )
(0) G6
11 21
0
4
14
11
0
2. 矩阵 D(0)中最小距离元素为 3 ,它是 G1( 0) 和
(0) G2 之间的距离,将它们合并为一类,得新的
G1( 2 ) G1( 2 )
( 2) G2 ( 2) G2
G3( 2 )( 2)Fra bibliotekG40
6 5 8
0
13 6
G3( 2 )
( 2) G4
0
7
0
4. 同理,得
( 3) ( 2) ( 3) ( 2) G1(3) {G1( 2 ) , G3( 2 ) } , G2 {G4 } {G2 } , G3
(2)
最长距离法:设 H 和 K 是两个聚类,则两类
间的最长距离定义为:
D H ,K max{d u ,v }, u H, v K
其中 du,v 的含义与上面相同。
递推运算:假若 K 类是由 I 和 J 两类合并而成, 则
DH , I max{d m , n }, m H , n I DH , K max{DH , I , DH , J } DH , J max{d m , n }, m H , n J
求得距离矩阵 D(3)
G1( 3)
( 3) G2
G3(3)
G1( 3)
( 3) G2
0
6 7
0
6
G3(3)
0
此时得到最终分类结果: {x1, x2, x4}、{x3}、{x5, x6}
聚类准则函数 最短距离法:设 H 和 K 是两个聚类,则两类 间的最短距离定义为:
(1)
D H ,K min{d u ,v }, u H, v K
3. 矩阵 D(1)中最小距离元素为 4 ,它是 G4(1) 和
G5(1) 之间的距离,将它们合并为一类,得到新的
分类为
( 2) (1) G1( 2 ) {G1(1) } , G2 {G2 },
( 2) (1) G3 {G3 } , G4
( 2)
(1) {G4 , G5(1) }
同样,按最小距离准则计算距离矩阵 D(2)
降维方法 设有 N 个样本,它们的特征维数是 n,则有 n×n 维的相关矩阵
R = [rij]nxn
其中,rij 是第 i 维与第 j 维特征之间的相关系数:
ij rij ii jj
这里:σii 和 σjj 分别是第 i 个和第 j 个分量的标准差, λij 是第 i 个和第 j 个分量的协方差。 分析: (1)根据相关系数的性质: 0 rij 1 (利 用柯西不等式证明) (2)rij = 0:表示两个分量完全不相关 (3)rij = 1:表示两个分量完全相关
其中,du,v 表示 H 类中的样本 xu 和 K 类中的样 本 xv 之间的距离,DH,K 表示 H 类中的所有样本 和 K 类中的所有样本之间的最小距离。 递推运算:假若 K 类是由 I 和 J 两类合并而成, 则
DH , I min{d m,n }, m H , n I DH , K min{DH , I , DH , J } DH , J min{d m,n }, m H , n J
(3)
中间距离法:设 K 类是由 I 和 J 两类合并而
成,则 H 和 K 类之间的距离为:
D H ,K
1 2 1 1 2 D H ,I D 2 D I ,J H ,J 2 2 4
它介于最长距离和最短距离之间。 (4) 重心法:假设 I 类中有 nI 个样本,J 类中有 nJ 个样本,则 I 和 J 合并后共有 nI+nJ 个样本。 用 nI/(nI+nJ)和 nJ/(nI+nJ)代替中间距离法中的系 数,得到重心法的类间距离计算公式:
1. 将每个样本单独看成一类,得
(0) G1( 0 ) {x1 } , G2 {x 2 } , G3( 0 ) {x3 } ,
(0) (0) {x 6 } G4 {x 4 } , G5( 0 ) {x5 } , G6
计算各类之间的距离,得距离矩阵 D(0)
G1( 0 ) G1( 0 )
到聚类中心 z1, z2, …。 第一步: 任取一样本 xi 作为一个聚类中心的初始值,例如令 z1 = x1 计算 D21 = || x2 - z1 || 若 D21 > T,则确定一个新的聚类中心 z2 = x2 否则 x2 属于以 z1 为中心的聚类 第二步:假设已有聚类中心 z1、z2 计算 D31 = || x3 - z1 || D32 = || x3 - z2 || 若 D31 > T 且 D32 > T,则得一个新的聚类中心 z3 = x3 否则 x3 属于离 z1 和 z2 中的最近者 ······ 如此重复下去,直至将 N 个模式样本分类完毕。
x z ( x T x )(z T z) = {x 中具有的特征数目
和 z 中具有的特征数目的几何 平均} 因此,在特征取值为 0 和 1 的二值情况下,S(x, z)等于 x 和 z 中具有的共同特征数目的相似性测 度。
最近邻规则的试探算法 给定 N 个待分类的模式样本{x1, x2, …, xN},要求按距离阈值 T,将它们分类
D H ,K nJ n In J nI 2 D2 D D2 H ,I H ,J I ,J 2 nI nJ nI nJ (n I n J )
(5)
类平均距离法:若采用样本间所有距离的平
均距离,则有:
D H ,K
1 nH nK
d
iH jK
2 ij
递推运算公式:
D H ,K nJ nI D2 D2 H ,I H ,J nI nJ nI nJ
分类
(1) (0) (0) {G3( 0 ) } , G3(1) {G4 }, G1(1) {G1( 0 ) , G2 } , G2 (1) (0) G4 {G5( 0 ) } , G5(1) {G6 },
计算聚类后的距离矩阵 D(1)。因 G1 为 G1 和
(0) (0) G2 两类合并而成,按最小距离准则,可分别计算
一种聚类准则函数 J 的定义
J x mj
j1 xS j
c
2
其中,c 为聚类类别的数目, Sj 为第 j 个类别的样本集合,
mj 1 Nj
D ( x 1 z1 ) 2 ( x 2 z 2 ) 2
显然,模式 x 和 z 之间的距离越小,它们越 相似。欧氏距离的概念和习惯上距离的概念是 一致的。 马氏距离 设 x 是模式向量,m 是均值向量,C 为模式 总体的协方差矩阵,则马氏距离的表达式:
D 2 ( x m) T C 1 ( x m)
病人的病程 0 ~ 代表病程 <= 1 个月 1 ~ 代表 1 个月< 病程 <= 6 个月 2 ~ 代表 6 个月< 病程 <= 12 个月 3 ~ 代表病程 > 12 个月
欧氏距离 设 x 和 z 为两个模式样本,其欧氏距离定义
为:D = || x - z || 例:x = (x1, x2),z = (z1, z2),则
第五步: 若有 z3 存在,则计算 max{min(Di1, Di2, Di3), i = 1,2,…,N}。若该值超过||z1 - z2 ||的一 定比例,则存在 z4,否则找聚类中心的过程 结束。 在此例中,无 z4 满足条件。 第六步:将模式样本{xi, i = 1,2,…,N}按最近距离 分到最近的聚类中心: z1 = x1:{x1, x3, x4}为第一类 z2 = x6:{x2, x6}为第二类 z3 = x7:{x5, x7, x8, x9, x10}为第三类 最后,还可在每一类中计算各样本的均值,得 到更具代表性的聚类中心。