位似图形的定义,画法及其计算.pptx

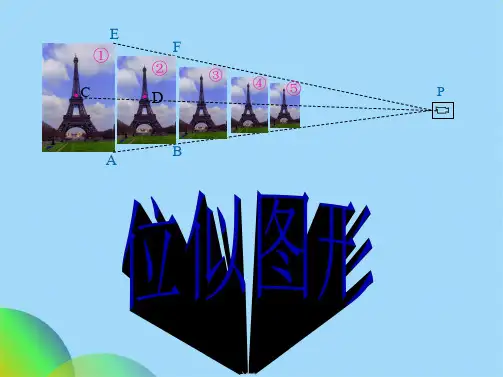
对应线段平行（或在一条直线上）.
我们学过的图形变换有： 平移，轴对称，旋转，位似。
（1）平移：
上下移：横坐标不变，纵坐标随之平移
左右移：纵坐标不变，横坐标随之平移
（2）轴对称 关于x轴对称：横坐标不变，纵坐标互为相反数 关于y轴对称：纵坐标不变，横坐标互为相反数 （3）旋转 绕原点旋转180度（中心对称）：横坐标、纵坐标都互 为相反数
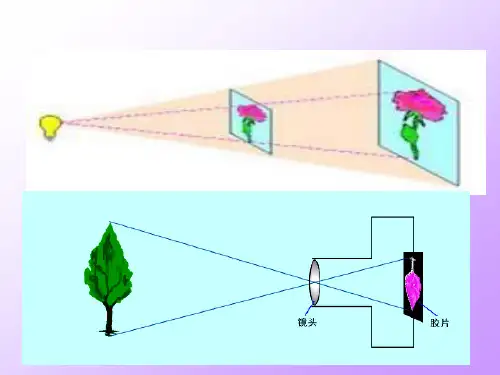
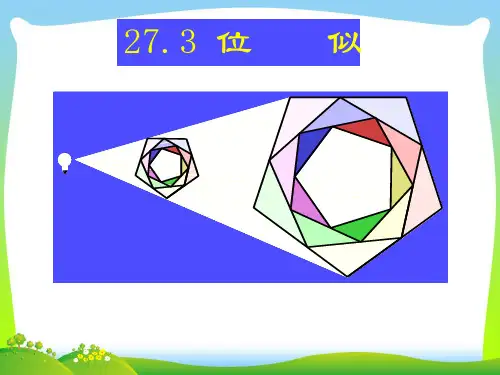
利用位似可以把一个图形放大或缩小
（3）位似图形中的对应线段平行（或在一条直线上）.
在平面直角坐标系中，如果位似变换
ቤተ መጻሕፍቲ ባይዱB’
分别观察这五个图，你发现每个图中的两个四边形B各对应点的连线有什么特征？对应边有何位置关系？
xA’=xA×(-k) ，yA'=yA×(-k)
如果两个图形不仅O相似，而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形位似比.
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O
为位似中心,相似比为1:3,把线段AB缩小.
y
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
（2）位似图形上任意一对对应点到位似中心的 距离之比等于相似比.
（3）位似图形中的对应线段平行（或在一条直线上）.
• 若△ABC与△A’B’C’的相似比为：1:2，
则OA：OA’=（ ）。 一对对应点到位似中心的距离之比等于位似比
1:2
如图表示△AOB和把它缩小后得到的△COD,写出它们的相似比

五个图，看看它们有什么共同的特征？
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载
同时满足下面三个条件的两个图形 才叫做位似图形．三条件缺一不可．
1．位似图形的概念 如果两个相似图形的每组对应点所在的 直线都交于一点,对应边互相平行或重 合，那么这样的两个图形叫做位似图形 , 这个交点叫做位似中心, 这时两个相似 图形的相似比又叫做它们的位似比.
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载
思考：还有没其他作法？
C’ A'
B’
. O
B
A C
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载
探究3
如图，△ABC三个顶点坐 标分别为A（2，3），B （2，1），C（6，2），以 点O为位似中心，相似比 为2，将△ABC放大，观察 对应顶点坐标的变化，你 有什么发现？
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载探究2Fra bibliotek性质呢？
位似图形图形具有什么样的
A
C/
B/
B
O A/ C
人教版九年级下册数学《27.3 位似图形概念》课件 (共22张PPT)课件优秀课件ppt课件免费课件优秀 课件课 件下载

人教版九年级下册位似位似图形的概 念及画 法优质P PT
人教版九年级下册位似位似图形的概 念及画 法优质P PT
归纳：
两个相似多边形，如果它们对应顶点所在的直线相交 于一点，并且这点与对应顶点所连线段成比例,我们就把 这样的两个图形叫做位似图形，这个交点叫做位似中心．
人教版九年级下册位似位似图形的概 念及画 法优质P PT
① 两个图形相似. ②对应点的连线相交于一点，对应边互相 平行或在同一直线上.
③任意一对对应点到位似中心的距离之比 等于相似比.
作位似图形：关键是确定位似中心、相似 比和找关键点的对应点.
人教版九年级下册位似位似图形的概 念及画 法优质P PT 人教版九年级下册位似位似图形的概 念及画 法优质P PT
D O
C
G
人教版九年级下册位似位似图形的概 念及画 法优质P PT
F、G、H,使正方形ABCD与
人教版九年级下册位似位似图形的概 念及画 法优质P PT
5.如图所示，四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ， 且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应 边A′ B′所在的位置，请把四边形A′ B′ C′ D′其余部分补画上.
★ 位似图形的画法
例3 如图，已知△ABC，以点O为位似中心画△DEF，使
其与△ABC位似，且位似比为2.
解：画射线OA、OB、OC；
D
在射线OA、OB、OC上分别取点D、E、F，
使OD = 2OA，OE = 2OB，OF = 2OC；
A
顺次连结D、E、F,使△DEF与△ABC位似，
E
相似比为2.
B
归纳：
画位似图形的一般步骤： （1）确定位似中心； （2）分别连接位似中心和能代表原图的关键点并延长； （3）根据相似比，确定能代表所画的位似图形的关键点； （4）按照原图的形状，顺次连接上述各点，得到放大或缩 小后的图形.

点O就是它们的位似中心，位似比为 .

由作图还可以看到，
C
D
位似多边形必定是
C′
D′
相似多边形，位似比
A
也就是相似比.
B
A′
B′
O
11
11
探究新知
例1
判断下列各图形哪些是位似图形：
若是，请指出位似中心
(1)正五边形ABCDE与正五边形A'B'C'D'E'；
(1‘)五边形ABCDE与五边形A'B'C'D'E'；
E
x
-6
OA，OB，OC，OD，
-8
-10
F′
-12
G′
-14
就得到四边形G′C′E′F′，也是所求作的四
边形.
23
23
探究新知
如图，例题中平行四边形ABCD的顶点坐标分别为 A(0，4)，
B(2，0)，C(6，0)，D(4，4).
(1)写出平行四边形GCEF的各个顶点坐标.
y
14
G
F
12
10
8
G(0，12)，C(6，0)，
2.确定关键点（一般是多边形的顶点）；
3.找出新图形的关键点；
4.顺次连接各点，得到所求作的图形.
18
18
探究新知
放缩尺是将图形进行放大或缩小的工具.
如图，点O位置固定不变，在A，A'处装
有画笔.当画笔A沿图形F运动时，画笔A'
画出图形F'，图形F'将图形F放大了.反之，
图形F是图形F'的缩小图形.
△ABO扩大到原来的2倍，得到△A′B′O．若点A的坐标是

1对称图形,中心对称与中心对 称图形)：对称轴,对称中心. 平移：平移的方向,平移的距离. 旋转：旋转中心,旋转方向,旋转角度. 相似：相似比.
注：图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
概念与性质 2. 位似图形的性质
从第 (1)，(2)图中，我们可以看到，△OAB∽△O A′B′,
则OOAA′ ＝OOBB′ ＝A′ABB′ .从第（3）图中同样可以看到
AF AD
＝AAPC
＝AABE
＝EBPC
＝FDPC
性质：位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
• 若△ABC与△A’B’C’的相似比为：1:2， 则OA：OA’=（ 1:2 ）。
译：同心协力的人，他们的力量足以把坚硬的金属弄断；同心同德的人发表一致的意见，说服力强，人们就像嗅到芬芳的兰花香味，容易接受。
11．君子藏器于身，待时而动。 ——《周易》
译：君子就算有卓越的才能超群的技艺，也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。
12．满招损，谦受益。 ——《尚书》
A’
A
B
B’
O
C
C’
利用位似，可以将一个图形放大或缩小．
例如，要把四边形ABCD缩小到原来的1/2， 1.在四边形外任选一点O（如图），
2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D'， 使得 OA' OB' OC' OD' 1
OA OB OC OD 2 3.顺次连接点A'、B'、C'、D'，所得四边形A'B'C'D' 就是所要求的图形．

对应边平行
位似图形的探究3
再探究这两个相似图形，对同学们来说已经不 是难事了，我们完全有能力自己去探究！
对应点连线相交于一点
对应边平行
定义及性质：
如果两个相似图形的 对应点连线相交于一点， 并且对应边互相平行， 这样的两个图形叫 位做 似图形 ， 这个交点叫位做似中心 。
对应点连线相交于一点
B(6,0),
A
以原点O为位似中心，
相似比为1/3，把线段缩小。
观察对应点之间的坐标的变化，
A’
你有什么发现？
O
B’
B’’
B
A’’
归纳：
在平面直角坐标系中， 如果位似变换是以原点为位似中心， 相似比为k， 那么位似图形对应点的坐标的比等于k或-k
例如：点A的对应点为A’，则A’点的坐标可以
这样确定。
•
17、一个人即使已登上顶峰，也仍要 自强不 息。2021/2/272021/2/272021/2/272021/2/27
谢谢观赏
You made my day!
我们，还在路上……
二、位似图形的画法
以0为中心把△ABC 缩小为原来的一半。
O C’
B’
A’
A B
C
练习：如图：以O为位似中心， 将△ABC放大为原来的两倍
O B'
B A
C
C'' A''
B A'
A
O
C
C'
如果B把'' 位似图形放到直角体系中，又如何 去探究位似变换与坐标之间的关系呢？
三 、位似变换与坐标的关系
在平面直角体系中有两点A(6,3)、

位似比
知识点2 位似图形的性质
明 相似 确 对应顶点的连线相交于一点
位似中心
O
辨析 位似的特征：
1．位似图形一定是相似图形，反之相 似图形不一定是位似图形 .
2．判断位似图形时，要注意首先它们 必须是相似图形，其次每一对对应点所在 直线都经过同一点 .
判断
下面哪些相似图形是位似图形？
√
√
× √×
位似图形的概念及画法 九年级下册
新课导入
在日常生活中，我们经常见到这样一类相 似的图形，它们有什么特征？
在日常生活中，经常遇到一些把图形放大或 缩小，但不改变图形的形状的情形.经过放大或 缩小的图形，与原图形是相似的.用这样的方法， 我们可以得到真实的图片和满意的照片.
这样的图形有 什么特点呢？
2.分别在线段 OA，OB，OC，OD 上取A′，B′，
C′，D′，使得OA′ = OB ′ = OC ′ = OD ′ = 1 . OA OB OC OD 2
3.顺次连接点A′，B′，C′，
A
D′，所得四边形A′B′C′D′就是所
B A＇
D
要求的图形。
B＇ D＇ C C＇
O
作法二：
如果在四边形外任选一点O，分别在OA，OB，
B.AOC来自A′C′基础巩固
随堂演练
1.下列说法不正确的是（ D ） A.位似图形一定是相似图形 B.相似图形不一定是位似图形 C.位似图形上任意一对对应点到位似中心的距离
之比等于相似比
D.位似图形中每组对应点所在的直线必相互平行
2.用作位似图形的方法，可以将一个图形放 大或缩小，位似中心（ D ） A.只能选在原图形的外部 B.只能选在原图形的内部 C.只能选在原图形的边上 D.可以选择任意位置

在位置关系上还符合以下条件：(1)对应顶点的连线都经过同
一点；(2)对应边互相平行或共线.
判别两个图形位似的关键是寻找位似中心，位似中心可以
在两个图形的同侧、两个图形之间或两个图形内，还可以在
其中一个图形的边或顶点上.
人教版数学九年级下册
知识精讲
如何将一个图形放大或缩小，你有哪些方法？
利用位似，可以将一个图形放大或缩小.
(2)求所作的矩形的面积.
解: (2)设IK与CD交于N,，所作矩形的宽IJ=x，则IK=2x.
∵IK∥AB，
∴△CIK∽△CAB
∵CN、CD分别是△CIK、△CAB的高

∴ =

60− 2
即
= ,
60 80
解得x=24
∴该矩形的长为48，宽为24
∴S矩形IJLk=24×48=1152
的位似图形是(A )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
达标检测
人教版数学九年级下册
5.如图，已知四边形ABCD，将图形各边放大到原来的三倍.
(你有几种方法)
解法一:四边形A'B'C'D'为所要求的图形.
达标检测
人教版数学九年级下册
5.如图，已知四边形ABCD，将图形各边放大到原来的三倍.
(你有几种方法)
解法四:四边形A'B'C'D'为所要求的图形.
人教版数学九年级下册
达标检测
6.一般在室外放映的电影胶片上每一个图片的规格
为:3.5cm×3.5cm，放映的银屏的规格为2m×2m，若影机的
光源距胶片20cm时，问银屏应在离镜头多远的地方，放映

D
C
A
平行或在一条直线上 对应线段_______________________________
练习与拓展
1．如图，已知△ABC和点O.以O为位似中心，求作 △ABC的位似图形，并把△ABC的边长扩大到原来的两倍. A' .
A
O. B B’ C C’
OA:OA’ =OB:OB’ =OC:OC’= 1:2
A B C D G F E● NhomakorabeaP
G′
F′
A′
C′
B′
顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的 箭头)就是符合要求的图形。
观 察
它们相似的共同 点是什么？
其中相似图形的 共同点是什么？
概念与性质
1．位似图形的概念
如果两个图形不仅相似，而且每组对应点所在的
直线都经过同一点,对应边互相平行,或者在同一 条直线上，那么这样的两个图形叫做位似图形,这 个点叫做位似中心. 相似 对应点的连 线相交一点 对应边平行或 同一条直线上
思考：是否相似图形都是位似图形？ 位似图形都是相似图形吗？
想一想
判断下面的正方形是不是位似图形？
A D
不是
E （1） B C F G
显然，位似图形是相似图形的特殊情形.相似图形不 一定是位似图形，可位似图形一定是相似图形
思考：位似图形有何性质？
学习应用
如何把三角形ABC放大为原来的2倍 E ?
B O C A F D O F E 位似中心 对应点连线都交于____________ B
性质：两个位似的图形上每一对对应点都与位似中心 在一条直线上，并且新图形与原图形上对应点到位似 中心的距离之比等于相似比

部编版九年级下册数学课件
第二章 位似
2.4.1 位似图形的
概念及画法
TOPIC 2.4.1 The concept and drawing of bit-like graphics
讲师：X.X
CONTENTS
01
学习目标
1.理解位似图形的概念，理解位似变化是特殊的相似变化。
2. 会画位似图形，能够根据位似比的大小把一个图形放大或缩小。
的两个图形叫做位似图形，这个交点叫做位似中心．
① 两个图形相似.
位似图形的概念
及画法
性质
②对应点的连线相交于一点，对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
等于相似比.
画法
作位似图形：关键是确定位似中心、相似
比和找关键点的对应点.
部编版九年级下册数学课件
第二章 位似
2.4.1 位似图形的
4.已知边长为1的正方形ABCD，以它的两条对角线的交点为位似中心，画一个
边长为2且与它位似的正方形.
E
解：画射线OA、OB、OC、OD;在射线OA、
A
OB、OC、OD上分别取点D、E、F,使OE =
D
O
2OA , OF = 2OB , OG = 2OC , OH = 2OD;
B
顺次连结E、F、G、H,使正方形ABCD与正方
如果是，请说明理由并求出相似比.
02
知识讲解
解：∵ 四边形ABCD 和四边形A′ B′ C′ D′位似，
∴ 四边形ABCD ∽四边形A′ B′ C′ D′ .
∵ 四边形A′ B′ C′ D′和四边形A″ B″ C″ D″位似，
∴ 四边形A′ B′ C′ D′∽四边形A″ B″ C″ D″ .