下载文档原格式
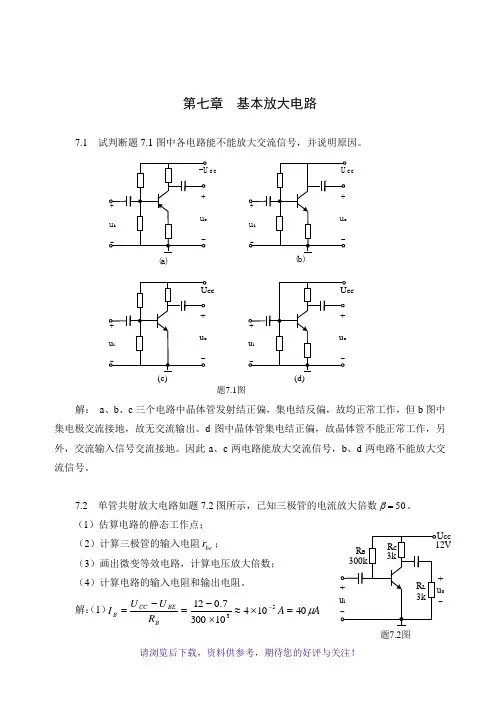
第七章 基本放大电路7.1 试判断题7.1图中各电路能不能放大交流信号，并说明原因。
解： a 、b 、c 三个电路中晶体管发射结正偏，集电结反偏，故均正常工作，但b 图中集电极交流接地，故无交流输出。
d 图中晶体管集电结正偏，故晶体管不能正常工作，另外，交流输入信号交流接地。
因此a 、c 两电路能放大交流信号，b 、d 两电路不能放大交流信号。
7.2 单管共射放大电路如题7.2图所示，已知三极管的电流放大倍数50=β。
（1）估算电路的静态工作点； （2）计算三极管的输入电阻be r ；（3）画出微变等效电路，计算电压放大倍数； （4）计算电路的输入电阻和输出电阻。
解：（1）A A R U U I B BE CC B μ40104103007.01253=⨯≈⨯-=-=-CC +o -题7.2图C CC (a)题7.1图mA A I I B C 210210405036=⨯=⨯⨯==--βV I R U U C C CC CE 61021031233=⨯⨯⨯-=-=-（2）Ω=+=+=9502265030026300C Cbe I r β （3）放大电路的微变等效电路如图所示 电压放大倍数7995.03||350||-=-=-=be L C u r R R A β（4）输入电阻：Ω≈⨯==950950||10300||3be B i r R r输出电阻 Ω==k R r C 307.3 单管共射放大电路如题7.3图所示。
已知100=β （1）估算电路的静态工作点；（2）计算电路的电压放大倍数、输入电阻和输出电阻 （3）估算最大不失真输出电压的幅值；（4）当i u 足够大时，输出电压首先出现何种失真，如何调节R B 消除失真？解：电路的直流通路如图所示，CC BQ E BEQ BQ B U I R U I R =+++)1(βAmA R R U U I EB BEQ CC BQ μβ435.010130015)1(=⨯+≈++-≈由此定出静态工作点Q 为 mA I I BQ CQ 3.4==β，V R R I U U E C C CC CEQ 3.4)5.02(3.415)(≈+⨯-=+-=（2）Ω=⨯+=9053.426100300be r 由于R E 被交流傍路，因此16690.05.1100||-=⨯-=-=be L C u r R R A βΩ≈==k r R r be B i 9.0905.0||300||+u o -CC +u o -题7.3图CCRΩ==k R R C O 2（3）由于U CEQ =4.3V ，故最大不饱和失真输出电压为 V U U CEQ 6.37.03.47.00=-=-=' 最大不截止失真输出电压近似为V R I U L CQ 4.65.13.40=⨯='⋅='' 因此，最大不失真输出电压的幅值为3.6V 。
《电路与模拟电子技术基础 习题及实验指导答案 第二版》第1章 直流电路一、填 空 题1.4.1 与之联接的外电路；1.4.2 1-n ，)1(--n b ；1.4.3 不变；1.4.4 21W ，负载；1.4.5 Ω1.65A ， ；1.4.6 1A 3A ， ； 1.4.7 3213212)(3)23(R R R R R R R +++=； 1.4.8 1A ；1.4.9 Ω4.0，A 5.12；1.4.10 电压控制电压源、电压控制电流源、电流控制电压源、电流控制电流源；1.4.11 3A ；1.4.12 3A ；1.4.13 Ω2；1.4.14 15V ，Ω5.4；1.4.15 V 6S =U 。
二、单 项 选 择 题1.4.16 C ； 1.4.17 B ； 1.4.18 D ； 1.4.19 A ；1.4.20 A ； 1.4.21 C ； 1.4.22 B ； 1.4.23 D 。
第2章一阶动态电路的暂态分析一、填 空 题2.4.1 短路，开路；2.4.2 零输入响应；2.4.3 短路，开路；2.4.4 电容电压，电感电流；2.4.5 越慢；2.4.6 换路瞬间；2.4.7 三角波；2.4.8 s 05.0，k Ω25； 2.4.9 C R R R R 3232+； 2.4.10 mA 1,V 2。
二、单 项 选 择 题2.4.11 B ； 2.4.12 D ； 2.4.13 B ；2.4.14 D ； 2.4.15 B ； 2.4.16 C 。
第3章 正弦稳态电路的分析一、填 空 题3.4.1 ︒300.02s A 10， ， ； 3.4.2 V )13.532sin(25)(︒+=t t u ；3.4.3 容性， A 44；3.4.4 10V ，2V3.4.5 相同；3.4.6 V 30，20V ；3.4.7 A 44，W 7744；3.4.8 A 5；3.4.9 减小、不变、提高；3.4.10 F 7.87μ；3.4.11 20kVA ，12kvar -；3.4.12 不变、增加、减少；3.4.13 电阻性，电容性； 3.4.14 LC π21，阻抗，电流；3.4.15 1rad/s ，4；3.4.16 Ω10；3.4.17 P L U U =，P L 3I I =，︒-30； 3.4.18 P L 3U U =，P L I I =，超前。
20XX年复习资料大学复习资料专业：班级：科目老师：日期：习 题 77.1 确定图7.1所示电路的漏极电流。
VTR D+DDV V P = -6V I DSS =3mA VTR D-DDV V P = 6V I = -12mA(a)(b)图7.1 习题7.1图(a) U GSQ =－2V ，mA)(33.1)621(3)1(P GS DSS D =-⨯=-=U U I I (b) U GSQ =3V ，I D =－20XXXX ×(1－3/6)=－3(mA)7.2 电路如图7.2所示，MOSFET 的U T = 2V ，K = 50mA/V 2，确定电路Q 点的I DQ和U DSQ 值。
)V (13.3241510015DD g2g1g2GSQ =⨯+=⨯+=V R R R U)mA (9.63)213.3(50)(22T GSQ DQ =-⨯=-=U U K I)V (2.112.09.6324d DQ DD DSQ =⨯-=-=R I V U7.3 试求图7.3所示每个电路图的U DS ，已知|I DSS | = 8mA 。
(a) U GSQ =0(V) I DQ =I DSS =8(mA) U DSQ =V DD －I DQ R d = 20XXXX －8×1=4(V)(b) U GSQ =0(V) I DQ =I DSS =8(mA) U DSQ =V DD －I DQ R d = 20XXXX －8×1.2=5.4(V) (c) U GSQ =0(V) I DQ =I DSS =－8(mA) U DSQ =V DD －I DQ R d = －9+8×0.56=－4.52(V)R g1VT+V DD 24VR g2100k 15k ΩR d 200ΩVT+V DD 12VR g 10M ΩR d 1.0k ΩVT+V DD 15V R g 10M ΩR d 1.2k ΩVT+V DD -9V R g 10M ΩR d 560Ω(a)(b)(c)图7.2 习题7.2电路图 图7.3 习题7.3电路图7.4 某MOSFET 的I DSS = 20XXXXmA 且U P = －8V 。
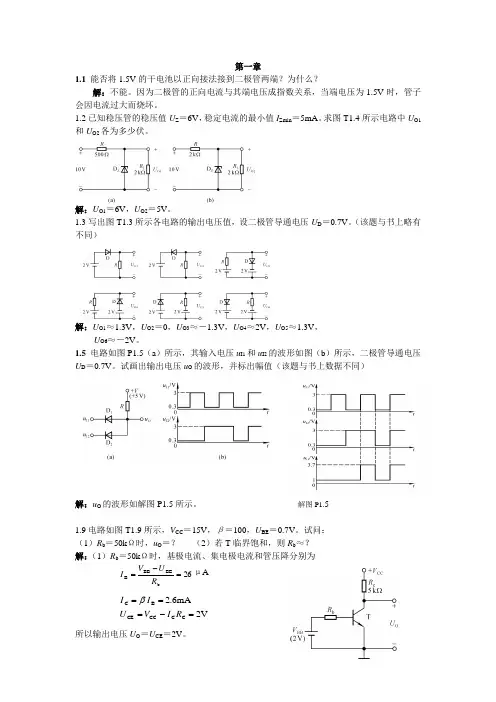
第一章1.1 能否将1.5V 的干电池以正向接法接到二极管两端？为什么？解：不能。
因为二极管的正向电流与其端电压成指数关系，当端电压为1.5V 时，管子会因电流过大而烧坏。
1.2已知稳压管的稳压值U Z ＝6V ，稳定电流的最小值I Zmin ＝5mA 。
求图T1.4所示电路中U O1和U O2各为多少伏。
解：U O1＝6V ，U O2＝5V 。
1.3写出图T1.3所示各电路的输出电压值，设二极管导通电压U D ＝0.7V 。
（该题与书上略有不同）解：U O1≈1.3V ，U O2＝0，U O3≈－1.3V ，U O4≈2V ，U O5≈1.3V ，U O6≈－2V 。
1.5 电路如图P1.5（a ）所示，其输入电压u I1和u I2的波形如图（b ）所示，二极管导通电压U D ＝0.7V 。
试画出输出电压u O 的波形，并标出幅值（该题与书上数据不同）解：u O 的波形如解图P1.5所示。
解图P1.51.9电路如图T1.9所示，V CC ＝15V ，β＝100，U BE ＝0.7V 。
试问： （1）R b ＝50k Ω时，u O ＝？ （2）若T 临界饱和，则R b ≈？ 解：（1）R b ＝50k Ω时，基极电流、集电极电流和管压降分别为26bBEBB B =-=R U V I μAV2mA 6.2 C C CC CE B C =-===R I V U I I β所以输出电压U O ＝U CE ＝2V 。
1.11电路如图P1.11所示，试问β大于多少时晶体管饱和？ 解：取U CES ＝U BE ，若管子饱和，则Cb C BECC b BE CC R R R U V R U V ββ=-=-⋅所以，100Cb=≥R R β时，管子饱和。
图1.11 1.12 分别判断图P1.12所示各电路中晶体管是否有可能工作在放大状态第二章2.1试分析图T2.2所示各电路是否能够放大正弦交流信号，简述理由。
第1章 电 阻 电 路1.1 正弦交流电 交流电 1.2 电流 电压 功率 1.3 电压 电流 功率 1.4 幅值 相位 频率 1.5 幅值 相位 频率 1.622221.7 相电压 线电压 220V 380V 1.8 星型 三角形 1.9 31.10 超前 滞后 同相 1.1131.12——1.25 F F T T F F T F F T T F T T1.26 答：（1） 固定电阻器可分为碳膜电阻器、金属氧化膜电阻器、金属膜电阻器、线绕电阻器和贴片式电阻器等。
① 碳膜电阻器：碳膜电阻器以碳膜作为电阻材料，在小圆柱形的陶瓷绝缘基体上，利用浸渍或真空蒸发形成结晶的电阻膜（碳膜）。
电阻值的调整和确定通过在碳膜上刻螺纹槽来实现；② 金属氧化膜电阻器：金属氧化膜电阻器的电感很小，与同样体积的碳膜电阻器相比，其额定负荷大大提高。
但阻值范围小，通常在200Kω以下；③ 金属膜电阻器：金属膜电阻器的工作稳定性高，噪声低，但成本较高，通常在精度要求较高的场合使用；④ 线绕电阻器：线绕电阻器与额定功率相同的薄膜电阻相比，具有体积小的优点 ⑤ 贴片式电阻器：贴片式电阻器的端面利用自动焊接技术，直接焊到线路板上。
这种不需引脚的焊接方法有许多优点，如重量轻、电路板尺寸小、易于实现自动装配等。
（2） 电位器根据电阻体的材料分有：合成碳膜电位器、金属陶瓷电位器、线绕电位器、实心电位器等① 合成碳膜电位器：分辨率高、阻值范围大，滑动噪声大、耐热耐湿性不好； ② 金属陶瓷电位器：具有阻值范围大，体积小和可调精度高（±0.01%）等特点； ③ 线绕式电位器：线绕式电位器属于功率型电阻器，具有噪声低、温度特性好、额定负荷大等特点，主要用于各种低频电路的电压或电流调整；④ 微调电位器：微调电位器一般用于阻值不需频繁调节的场合，通常由专业人员完成调试，用户不可随便调节。
⑤ 贴片式电位器：贴片式电位器的负荷能力较小，一般用于通信、家电等电子产品中。
第三章 正弦交流电路两同频率的正弦电压，V t u V t u )60cos(4,)30sin(1021︒+=︒+-=ωω，求出它们的有效值和相位差。
解：将两正弦电压写成标准形式V t u )18030sin(101︒+︒+=ω V t u )9060sin(42︒+︒+=ω，其有效值为V U 07.72101==，V U 83.2242==︒=︒-︒=150,15021021ϕϕ或︒=-=∆6021ϕϕϕ已知相量21421321,,322,232A A A A A A j A j A &&&&&&&&⋅=+=++=+=，试写出它们的极坐标表示式。
解： ︒∠=⋅=⎪⎪⎭⎫⎝⎛+=︒304421234301j e j A & ︒∠=⎪⎪⎭⎫ ⎝⎛+=604232142j A &3122(21)(1)45A A A j j =+=++=+=∠︒&&& 412443060169016A A A j =⋅=⨯∠︒+︒=∠︒=&&& 已知两电流 A t i A t i )45314cos(5,)30314sin(221︒+=︒+=,若21i i i +=，求i 并画出相图。
解：A t i )9045314sin(52︒+︒+=，两电流的幅值相量为1230m I A =∠︒&，A I m︒∠=13552& 总电流幅值相量为)135sin 135(cos 5)30sin 30(cos 221︒+︒+︒+︒=+=j j I I I mm m &&& ︒∠=+-=++-=11285.453.480.1)2251(2253j jA t t i )112314sin(85.4)(︒+= 相量图如右图所示。
某二端元件，已知其两端的电压相量为V 120220︒∠=U &，电流相量为A I ︒∠=305&，f=50H Z ，试确定元件的种类，并确定参数值。
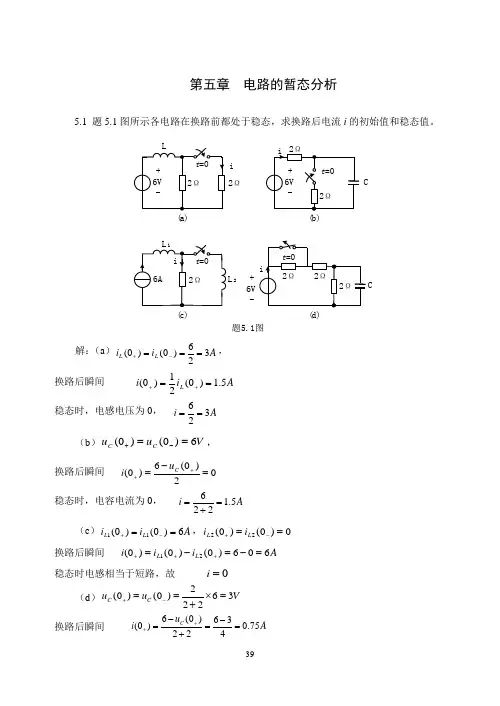
第五章 电路的暂态分析5.1 题5.1图所示各电路在换路前都处于稳态，求换路后电流i 的初始值和稳态值。
解：（a ）A i i L L 326)0()0(===-+，换路后瞬间 A i i L 5.1)0(21)0(==++ 稳态时，电感电压为0， A i 326==（b ）V u u C C 6)0()0(==-+， 换路后瞬间 02)0(6)0(=-=++C u i 稳态时，电容电流为0， A i 5.1226=+=（c ）A i i L L 6)0()0(11==-+，0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路，故 0=i（d ）2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+(a)(b)(d)(c)C2ΩL 2+6V -题5.1图i稳态时电容相当于开路，故 A i 12226=++=5.2 题5.2图所示电路中，S 闭合前电路处于稳态，求u L 、i C 和i R 的初始值。
解：换路后瞬间 A i L 6=，V u C 1863=⨯= 06=-=L R i i031863=-=-=C L C u i i0==+R C L Ri u u ，V u u C L 18-=-=5.3 求题5.3图所示电路换路后u L 和i C 的初始值。
设换路前电路已处于稳态。
解：换路后，0)0()0(==-+L L i i ，4mA 电流全部流过R 2，即(0)4C i mA +=对右边一个网孔有：C C L u i R u R +⋅=+⋅210由于(0)(0)0C C u u +-==，故2(0)(0)3412L C u R i V ++==⨯=5.4 题5.4图所示电路中，换路前电路已处于稳态，求换路后的i 、i L 和 u L 。
第2章一阶动态电路的暂态分析习题解答。
图2.1 习题2.1图解电流源电流为⎪⎩⎪⎨⎧<<-<<=其他2s11A1s1A)(Sttti分段计算电容电压)(tus10<≤t期间()V2d5.01d)(1)0()(⎰==⎰+=tt tiCutuλλλs1=t时，V2)1(=us21≤≤t期间()V24)1(22d)1(5.01)1()(1ttutu t-=⎰--=⨯-+=λ2=t s时，0)2(=us2>t时⎰=⨯+=tutu2d5.01)2()(λ()()⎪⎩⎪⎨⎧≤≤-≤≤=其他2s1V241sV2)(tttttu瞬时功率为()()⎪⎩⎪⎨⎧<<-<<=⋅=其他2s1W421sW2)()()(tttttitutpS电容的储能为()⎪⎪⎩⎪⎪⎨⎧<<-<<==其他2s1J21sJ)(21)(222tttttCutw2.2在图2.2（a）中，电感H3=L，电流波形如图（b）所示，求电压u、s1=t时电感吸收功率及储存的能量。
图2.2 习题2.2图解由图2.2(b)可写出电流的函数()⎪⎩⎪⎨⎧≤≤-≤≤=其他2s1A21sA)(ttttt i⎪⎩⎪⎨⎧<<-<<==其他2s1V31sV3)(ttdtdiLtu1s=t时3W)1()1()1(==iupJ231321)1(21)1(22L=⨯⨯==Liw2.3 在图2.3所示电路中，已知()V4cos8ttu=，()A21=i，()A12=i，求0>t时的()t i1和()t i2。
图2.3 习题2.3电路图解()()A4sin2d4cos8212d21)0()(11ttuiti tt+=⎰+=⎰+=ττ()A 4sin 211d 4cos 841)0()(022⎪⎭⎫ ⎝⎛-=⎰-=t i t i t ττ 2.4 电路如图2.4(a)所示，开关在0=t 时由“1”搬向“2”，已知开关在“1”时电路已处于稳定。
求C u 、C i 、L u 和L i 的初始值。
（a ）动态电路 （b ）+=0t 时刻的等效电路图2.4 习题2.4电路图解 在直流激励下，换路前动态元件储有能量且已达到稳定状态，则电容相当于开路，电感相当于短路。
根据-=0t 时刻的电路状态，求得V 48222)0(C =⨯+=-u ，A 2228)0(L =+=-i 。
根据换路定则可知：V 4)0()0(C C ==-+u u ，A 2)0()0(L L ==-+i i用电压为)0(C +u 的电压源替换电容，电流为)0(L +i 的电流源替换电感，得换路后一瞬间+=0t 时的等效电路如图(b)。
所以1A )0(04)0(4C C ＝－， ++=+⋅i iV 4)0(0)0()0(2L L L ＝－， ＋+++=⋅u u i2.5 开关闭合前图2.5（a ）所示电路已稳定且电容未储能，0=t 时开关闭合，求)0(+i 和)0(+u 。
（a ）动态电路 （b ）+=0t 时刻的等效电路图2.5 习题2.5电路图解 由题意得，换路前电路已达到稳定且电容未储能，故电感相当于短路，电容相当于短路，A 16410)0(L =+=-i ，0)0(C =-u 。
由换路定则得：0)0()0(C C ==-+u u ，A 1)0()0(L L ==-+i i 。
换路后瞬间即+=0t 时的等效电路如图2.5(b)，求得 V 441)0(=⨯=+u ， A 321366)0(=⨯+=+i 2.6 电路如图2.6所示，开关在0=t 时打开，打开前电路已稳定。
求C u 、L u 、L i 、1i 和C i 的初始值。
图2.6 习题2.6电路图解 换路前电容未储能，电感已储能，所以-=0t 时刻的起始值 0)0(C =-u ，A 326)0(L ==-i 由换路定则得：0)0(C =+u ，A 3)0(L =+i A 1)0(422)0(L 1=⨯+=++i i A 2)0()0()0(1L C =-=+++i i iV 4)0(4)0(26)0(1L L -=--=+++i i u2.7 换路前如图2.7所示电路已处于稳态，0=t 时开关打开。
求换路后的L i 及u 。
图2.7 习题2.7电路图解 0<t 时，电感储能且达到稳定，电感相当于短路，求得A 41366636363)0(L =+⨯+⨯+=-i 由于电流L i 是流过电感上的电流，根据换路定则得A 41)0()0(L L ==-+i i 0>t 时，电感两端等效电阻为Ω=+=9630R时间常数τs 920==R L τ 由此可得0>t 时各电流和电压为A e 41e)0()(29L L tτt i t i --+== 0>t V e 23)(629L tt i u --==－ 0>t2.8 换路前如图2.8所示电路已处于稳态，0=t 时开关闭合。
求换路后电容电压C u 及电流i 。
图2.8 习题2.8电路图解 0<t 时，电容储能且达到稳定，电容相当于开路，求得V 6421)0(C =+⨯=-u根据换路定则得：V 6)0()0(C C ==-+u u 时间常数：s 2.02.01=⨯=τ 由此可得0>t 时各电流和电压为V e 6e)0()(5C C t τtu t u --+== 0>t()Ae6312415C tui-+=++=0>t2.9 换路前如图2.9电路已处于稳态，0=t时开关闭合。
求换路后电容电压Cu及Ci。
图2.9 习题2.9电路图解0<t时，电容无储能，即0)0()0(CC==-+uu>t时，利用叠加原理得V6233336333)(C=⨯+⨯+⨯+=∞u时间常数：s75.15.033332=⨯⎪⎭⎫⎝⎛+⨯+==CRτ由此可得0>t时各电流和电压为Ve16)(75.11C⎪⎪⎭⎫⎝⎛-=-ttu0>tAe712dt75.11CCtduCi-==0>t2.10 开关在0=t时关闭，求如图2.10所示电路的零状态响应()t i。
图2.10 习题2.10电路图解求从等效电感两端看进去的戴维南等效电路V1266432OC=-⨯++=UΩ=++⨯=66.36464R时间常数：121==RLτ零状态响应：()Ae161e1)(12OC ttRUt i---=⎪⎪⎭⎫⎝⎛-=τ0>t2.11在如图2.11所示电路中，开关闭合前电感、电容均无储能，0=t时开关闭合。
求0>t时输出响应u。
图2.11 习题2.11电路图解由换路定则可知：0)0()0(CC==-+uu，0)0()0(LL==-+ii电容稳态值：V422)(C=⨯=∞u时间常数：s15.02C=⨯=τ零状态响应：()Ve14e1)()(CCttutu---=⎪⎪⎭⎫⎝⎛-∞=τ电感稳态值：A2)(L=∞i时间常数：s3162L==τ零状态响应：()Ae12)(3Ltti--=()Ve12e44dd)()(3LCtttiLtutu--+-=+=0>t2.12在如图2.12所示电路中，开关接在位置“1”时已达稳态，在0=t时开关转到“2”的位置，试用三要素法求0>t时的电容电压Cu及i。
图2.12 习题2.12电路图解 开关在位置1时：V 46424)0(=⨯+=-C u ， 由换路定则得初始值：V 4)0()0(C C ==-+u u稳态值：V 2)3(424)(C -=-⨯+=∞u 时间常数：s 3414242=⨯+⨯=τ由三要素法得：[]V e 62e)()0()()(43C C C C ⎪⎪⎭⎫ ⎝⎛+-=∞-+∞=--+t tu u u t u τ0>tA e 3212343⎪⎪⎭⎫ ⎝⎛--=--=-t C u i 0>t 2.13 图2.13所示电路原已达稳态，0=t 开关打开。
求0>t 时的响应C u 、L i 及u 。
图2.13 习题2.13电路图解：（1）应用三要素法求电容电压 电容初始值：V 5.25101010)0()0(C C =⨯+==-+u u稳态值：V 5)(C =∞u 时间常数：s 1101.0C =⨯=τ所以 ()V e 5.25)(C tt u --= 0>t（2）应用三要素法求电感电流 初始值：A 25.1101051)0()0(L L =++==-+i i稳态值：A 1)(=∞i 时间常数：s 51L =τ 所以 ()A e25.01)(5L tt i -+=0>t()Ve25.1e5.25dd5LCtttiuu--+-=-=0>t2.14在开关S闭合前，如图2.14所示电路已处于稳态，0=t时开关闭合。
求开关闭合后的电流Li。
图2.14 习题2.14电路图解（1）应用三要素法求电感电流初始值：A21444)0()0(LL=+==-+ii稳态值：A3121444444)(L=⨯+⨯+=∞i时间常数：s21444443L=+⨯+=τ故得Ae6131)(2L⎪⎭⎫⎝⎛+=-tti0>t2.15在如图2.15所示的电路中，开关S闭合前电路为稳态，0=t时开关闭合，试求0>t时的)((t)CCtiu、及)(Lti。
图2.15 习题2.15电路图解（1）应用三要素法求电容电压初始值：V1)0()0(CC==-+uu稳态值：V 4.51)(C -=-=∞u时间常数：s 111C =⨯=τ故 ()V e 54)(C tt u -+-= 0>tA 5e CC t dtdu i －＝－=0>t （2）应用三要素法求电感电流 初始值：0)0()0(L L ==-+i i 稳态值： 2.5A 25)(L ==∞i 时间常数：s 31032324L =+⨯=τ 所以 A e 12.5)(103L ⎪⎪⎭⎫ ⎝⎛-=-t t i 0>t。
