当前位置：文档之家 › 第三章流体静力学演示教学

第三章流体静力学演示教学

  • 格式：ppt
  • 大小：1.96 MB
  • 文档页数：90

下载文档原格式

  / 90

合集下载

流体力学第三章流体静力学-PPT精品

流体力学第三章流体静力学-PPT精品

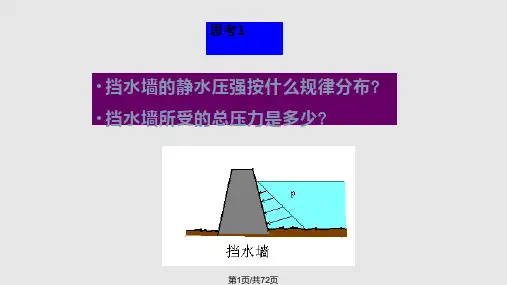
一、静止流体基本微分方程 如图3.1所示，静止流体中任意流体微团 所受的合力为零，即
f d A p n d A f d A n p d A (f p ) d 0
式中(f p)为作用于微元体积d 上的合力。因为是任意的，被积函数
pn
lim A0
Pn A
（3.1） 退 出
返回
n
P
n



A
F
图 3.1 作用于流体上的 力
第1页
第三章 流体静力学 第一节 作用于流体上的力
外界作用于该流体微团上的表面力为 A pn d A 。流体应力不仅与点的位置
有关，而且与通过该点的截面方位有关，也就是说，通过一点可以有不 同的流体应力。例如在直角坐标系中，某点的应力 px, py, pz 分别为通过该 点外法线单位向量为 i, j, k 截面上的应力。
d F ip d A xjp d A y k p d A z
即 d F x p d A x ,d F y p d A y ,d F z p d A z
整个曲面 A上的受力可由上式积分求得
F x A p d A x A (p a g)d h A x（3.16）
第3页
退出
返回
第三章 流体静力学
第四节 重力场中静止流体的压力，静止流体对物面的作用力
一、压力公式
重力场是最典型的质量力场。在重力场中，f g，若使直角坐标轴 z 与
地面的外法线重合，则重力场可写成 f kg
由（3.8）式 dpgdz
（3.9）
严格说来，式中g可以是 x,y,z,t的函数，但当所讨论的问题的时间和
(f p)是连续的，所以要满足上式，只可能 (f p) 处处为零。于是有

水力学流体静力学PPT课件

水力学流体静力学PPT课件

在水利工程中，液体相对平衡 的原理被广泛应用于水坝、水 库等水工建筑物的设计和施工 中。
在医学领域，液体相对平衡的 原理也被应用于血液动力学和 药物输送等方面的研究。
04
液体内部压强与浮力
Chapter
液体内部压强的计算
压强定义
单位面积上所受的压力，用p表示 ，单位为Pa。
计算公式
p = F/A，其中F为压力，A为受力 面积。
了解液体运动的描述方法和基本方程 ；
能够运用所学知识分析和解决工程实 际问题。
教学方法与手段
01
02
03
教学方法
采用讲授、讨论、案例分 析等多种教学方法相结合 的方式。
教学手段
使用PPT课件、动画演示 、实验演示等教学手段辅 助教学。
考核方式
采用平时成绩、期末考试 成绩和实验成绩相结合的 考核方式。
的气体量来调节浮力大小。
05
流体静力学在水利工程中的应 用
Chapter
水库水位与坝体稳定性分析
水库水位确定
根据水库地形、库容曲线 及入库流量等资料，确定 水库在不同运行条件下的 水位。
坝体稳定性分析
运用土力学、岩石力学等 原理，分析坝体在静水压 力、扬压力等作用下的稳 定性，确保大坝安全。
渗流控制
液体相对平衡是流体静力学研究的基础。
等压面的形成与性质
等压面是指在液体内部，压强相等的各点所组成的面。
在重力场中，等压面是一个水平面，因为在同一水平面上，各点受到的重力作用相 同，所以压强也相等。
等压面具有传递压强的性质，即等压面上的压强可以传递到液体内部的任意一点。
液体相对平衡的应用
液体相对平衡的原理可以应用 于测量液体的密度和深度。

第三章流体静力学

第三章流体静力学
一、静止液体作用在固体壁面上的总压力
作用在平面上总压力的计算方法有两种： 解析法
图解法
第二十六页，共八十九页。
1.平面总压力大小
o
设有一与水平面成α夹角的倾斜平面 ab，其面积为A，左侧受水压力， 水面大气压强为p0，在平板表面所 在的平面上建立坐标，原点o取在 平板表面与液面的交线上，ox轴与
hD hC yb
整理 p2p1gh
液体静力学基本方程式为 pp0 gh
第八页，共八十九页。
二.流体静力学基本方程的意义
1.A点的压强
p p 0g h p 0g (z 0 z )
整理
p
g
z
p0
g
z0
常数
意义：
Z——单位重量液体的位置势能(简称比位能)；
——p 静止液体中单位质量液体的压力能(简称比压能)
g
，比位能与比压能之和称为总比能。
3.运动流体是理想流体时，不会产生切应力，所以理想流体
动压强呈静水压强分布特性，即
第七页，共八十九页。
第二节 重力场中流体的平衡
一.流体静压强的基本方程
静止液体所受的力除了液体重力外 ，还有液面上的压力和固体壁面作 用在液体上的压力，其受力情况如 图所示。
1.受力平衡方程
p 2 A p 1 A g l A co 0 s
D
sin y2dA sinyc AyD
式中 y2dA 为受压面对ox轴的惯性矩 I X
所以
yD
Ix ycA
第三十二页，共八十九页。
根据平行移轴定理：
I X IC yC2 A
∴
yD
yc
Ic ycA
ohD hC h源自αa yyb

第三章 流体的运动(幻)

第三章 流体的运动(幻)

二、 稳定流动
研究流体运动通常有两种方法： 拉格朗日法——以流体的各个质元为 研究对象，根据牛顿定律研究每个质 元的运动状态随时间的变化。
5
欧拉法——研究各个时刻在流体流经过 的空间每一个点上流体质元的运动速度 的分布。
1、 稳定流动
流体在流动过程中的任一时刻，流体所占 据的空间中的每一个点都具有一定的流速， 其函数表达式为υ（x，y，z，t）。
Sυ是单位时间内通过任一截面S的
流体体积，常称为体积流量。
所以上式又称体积流量守恒定律。
13
对于不可压缩的流体来说，不仅质 量流量守恒，体积流量也是守恒的。 体积流量又可简称为流量，用Q来表示 Q=Sυ Q —— 指单位时间内通过流管中任一截 面的流体体积，其单位为（m3·-1）。 s
四、血流速度分布
1 1 2 2 p1 1 gh P2 2 2 2
则液体从小孔处流出的速度 为：
2 2 gh
与其从高度为h处自由下落时的速度 相等。上式就称为“托里折利公式”。
33
第三节 粘性流体的流动 一、 层流和湍流
粘性——实际流体在流动过程中总 是具有内摩擦力，表现出粘滞性， 简称粘性。因而它在流动过程中需 要克服内摩擦力作功而消耗能量。 粘性流体在运动时主要具有层流、湍 流和过渡流动三种运动形态。

2 gh

30
3、体位对血压的影响
若流体在等截面管中流动，若 其流速不变，由 伯努利方程得
P gh1 P2 gh2 1
P +ρgh = 常量
结论：高处的压强较小，而低处的 压强则较大。
31
压强与高度间的关系，可用来解释体 位因素对血压的影响。
32

第三章流体静力学(流体的平衡)

第三章流体静力学(流体的平衡)
第三章 流体静力学（流体的平衡）
1.流体的平衡：绝对平衡、相对平衡 2.流体平衡时的压强 3.流体平衡的条件 3.1.平衡的微分方程 ∂ p dx ∂ p dx −∂ p dydz − p dydz = dxdydz ∂x 2 ∂x 2 ∂x 表面力： −∇ p dxdydz d 体积力： f b =∇ p 绝对平衡方程： f x 方向表面力： p −
∫ gy sin dA= g sin ∫ y dA= g y c sin A= P c A
A A
设压力中心坐标为
x D , y D = x C f , y C e ,其中 f 和 e 称为纵向和横向偏心矩。
则总合力对形心坐标轴的力矩：
F e =∫ dF = g sin ∫ y dA F f =∫ dF = g sin ∫ y dA∇ p d r =0
d 考虑到绝对平衡方程，得出等压面的微分方程： f b r = 0 ，即在等压面上体力处处与等压面 垂直。
3.3.流体平衡的必要条件
b =∇× 由绝对平衡方程得 ∇× f 1 −1 ∇ p = 2 ∇ ×∇ p
−1 ∇ p⋅∇ ×∇ p =0 3 ⋅∇ × f =0 流体平衡的必要条件 f b b b⋅∇ × f b = 于是 f
均质流体 =constant
≡0 ∇× f b
−∇ =
1 ∇p
=
−p
非均质流体：正压流体 = p ，如等温或绝热气体 定义压力函数 P p ： ∇ P =
=∇ P 由绝对平衡方程得， f b 4.流体静力学基本方程（静力学规律）
由 P =− gz C 得
∇p p ≡0 ，故 f 有势，势函数 =− P p ∇× f b b

水力学 流体静力学PPT课件

水力学 流体静力学PPT课件
• 1).合力F的大小等于压强分布体 的体积，即 F = •b；
• 2).合力F的方向为垂直指向受压 面；
• 3).合力F的作用线通过压强分布 体的形心，作用线与受压面的交 点即为D点。
§2-2 流体静止的微分方程
一.流体静止的微分方程：
• 边长分别为dx,dy,dz的微元平行六面体受表面力和质量力的共同作用而保 持静止。
微元体的中心为A点，左表面的中 心为B点，右表面的中心为C点。 A 点的压强为p(x,y,z)。
x方向的静力平衡：
(p
1 2
p x
dx)dydz ( p
1 2
。 确定液体作用在平面上的总压力的大小、方向和作用点
一.解析法：
1.合力的大小：
dA上的相对压强：p γh γy sin θ dA上液体作用的合力为：dF pdA γy sin θdA
第34页/共72页
F dF y sin dA sin ydA
A
A
A
sin yc A hc A
计是一个水平倾角为的Π形管。
已知测压计两侧斜液柱读数的差值
为L=30mm，倾角 = 30°，试求压
强差p1 – p2 。 3)
(书上P29的例2-
解：
这里：z1 z2
p1 γ(z3 z1) γ(z4 z2 ) p2
p1 p2 γ(z3 z4 ) γL sin θ
第26页/共72页
dz
p0 p
R 0 T0 0.0065z
取：g = 9.807m/s²， = 0.0065K/m， R = 287 N•m/Kg•K，T0 = 288K。 则：
g
p p0
1
T0
R z
1

详细版流体力学-流体静力学.ppt


pm pab pa gh p
pv
c.真空度pv
pv pa pab
注意：pv表示绝对压强小于当地大气压强而形成 真空的程度，读正值！
.精品课件.
15
3.压强单位 标准大气压（atm） =1.013×105Pa=760mmHg=10.33mH2O 工程大气压（at） =0.9807×105Pa=735.5mmHg=10mH2O =1kg/cm2（每平方厘米千克力，简读公斤）
x y z 对（1）、（2）、（3）式坐标交错求偏导，整理得
X Y y x
Y Z z y
Z X x z
——力作功与路径无关的充分必要条件 必存在势函数U，力是有势力
dU
U x
dx
U y
dy
U dz .精品课z 件.
8
U X x
U Y y
U Z z
——力与势函数的关系
（4）式可写为：
换算： 1kPa=103Pa
1bar=105Pa
.精品课件.
16
4.测压计 一端与测点相连，一端与大气相连 例 求pA（A处是水，密度为ρ，测压 计内是密度为ρ’的水银）
解：作等压面
pA ga ' gh
pA 'h ag
例 求pA（A处是密度为ρ的空气，测压计内是密度为ρ’的 水）
解：pA ' gh
（1）用分割法求P大小，作用点为D；
或
yD
Jc yc A
h
Jc
sin
A
T
（从形心C处算起）
（2）对A点求矩
P
A
G l cos P AD Tl cos T
2
C l
D θ

第3章 流体静力学 (华水)


微分形式的等压面方程
f x dx f y dy f z dz 0
性质：在静止流体中，作用于任意点的质量力垂直于 经过该点的等压面
等压面及其特性：
等压面: 等压面性质:
1、在平衡液体中等压面就是等势面 p＝cons tan t dp 0 dU 0
液体中压强相等的点连成的面 （可能是曲面或平面）
方向特性
pc pc
pc
h
大小特性
静水压强的方向与受压面垂直并指向受压面
证明方法：……？？
反证法
特性二（大小特性）：静压强的大小与作用面在 空间的方位无关，只是坐标点的连续可微函数
即作用于同一点上各方向的静水压强大小相等。
边长 δx、δy、δz 静压强 px、py、pz和pn
密度 ρ
单位质量力的分量 fx 、fy、fz
1 p 0 z

2 p f x 不可压缩均质 y yx 2 p f y xy x
fx fy y x
单位质量力分量之间有下述关系
f y f x x y
f x f z z x
5.255
二 大气压的压强分布（可压缩流体中压强的变化）
在大气层中,从高11000m到20100m的空间为大气恒温层,
等温过程,气体的密度：

p RT
重力场中单位质量力分量为： 代入压差公式,得
dp p gdz RT1
f x f y 0, f z g
积分
dp RT1 gdz 0 p
用液柱高度表示 hV
pV p p a g g
三 绝对压强 计示压强(相对压强) 真空(真空度)

流体静力学课件


单管测压计缺点 被测压强不能太大 只能测量液体压强 被测压强必须高于当地大气压强
流体力学
U型管测压计1
p Am 2 gh 2 1 gh 1
作等压面
被测点
相界面
等高的两点必须在连 通的同一种液体中
沿液柱向上，压强减小。 液柱向下，压强增大 流体力学
U型管测压计2
U型管测压计特点 测量范围较大 可测量气体压强
z
在 x 方向上：
dy
dx 2
坐标为
A ( x
, y, z )
p dx x 2
dz
A(x,y,z)
y
压强为
pA' ( p
)
流体力学
x
建立液体的平衡微分方程
后 平面中心点的坐标增量为： z
在 x 方向上：
x
dx 2
, y 0, z 0
dy dz
坐标为
A ( x
p lim P A
P
A 0
流体静压强的方向垂直于 作用面，并指向流体内部
p
B
ΔS
s
流体力学
证明 静压强特性一
证: (反证法）
在流体中取一微元，用任意
P
p
Pn
平面切 割，取下部脱离体。
1）假设切割平面某点处的压强 P 不 沿内法线方向 则分解为
pn p
矛盾 ?
故只能沿法向
工程单位制：大气压(at、atm), 巴(bar), 液柱高度。
1atm = 1.013105Pa = 760 mm(Hg) = 10.33 m(H2O)
标准大气压
1at = 1kgf/cm2 = 0.981105Pa = 10 m(H2O)

第3讲 流体静力学基本方程式的应用


以上，以维持两扩大室内液面等高。
(2) 指示液要求：A、C不互溶，不起化 学反应，B与C亦不互溶，且A、C密度 差越小，R值就越大，读数精度也越高。 注：若两小室内液面差不可忽略时，则： p p1 p2 ( A C ) gR RC g 式中 ΔR=R(d/D)2为小室的液面差，d为U管内径，D为小室内径。
例：水在如图示的管道内流动。 在管道截面处连接一U管压差计， 指示液为水银，读数R=200mm、 h=1000mm。当地大气压强为 101.33×105Pa，试求流体在该截 面的压强。如右图示。 解：A-A’为等压面，则：
pA pA' pa
PA p H2 0 gh Hg gR
课堂练习：采用普通U管压差计测量某气体管路上两点的压强
差，指示液为水，读数R=10mm。为了提高测量精度，改用双 液体U管微压差计，指示液A为含40%乙醇的水溶液，密度ρA为 910kg/m3，指示液C为煤油，密度ρC为820kg/m3。试求双液体 U管微压差计的读数可以放大的倍数？已知水的密度为
可得到较大的读数R。

p p1 p2 R( A ) g R1 sin ( A ) g
A
④双液体U形管压差计（微差压差计）
目的：在测量微压差Δp时，可得到较大的读数R。 要求：
p p1 p2 ( A C ) gR
(1) 扩大室内径应大于U形管内径的10倍
p/ρ和 gz 分别表示单位质量流体所具有的静压能（J/kg）和位能
（J/kg）； （ p/ρ+ gZ ）——总势能。在同一种静止流体中不同 高度上的点其静压能和位能各不相同，但总势能保持不变。 （ 2）等压面
由 p po gh 当容器液面上方的压强p0一定时，静止液
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
适用范围：测压管适用于测量较小的压强， 但不适合测真空。
应当注意：
1.由于各种液体重度不同，所以仅标明高度尺寸不能代表压力 的大小，还必须同时注明是何种液体的液柱高度才行。
2.测压管只适用于测量较小的压力，一般不超过10kPa。用 于测量较小的压力，一般不超过10kPa。如果被测压力较高， 则需要加长测压管的长度，使用就很不方便。
3.测压管中的工作介质就是被测容器(或管道)中的流体，所 以测压管只能用于测量液体的正压，而对于测量液体的负压 以及气体的压力则不适用。
4.在测量过程中，测压管一定要垂直放置，否则将会产生测 量误差。
二、U形测压计
这种测压计是一个装在刻度板上的 两端开口的U型玻璃管。测量时， 管的一端与大气相通，另一端与被 测容器相接(如图)，然后根据U型 管中液柱的高度差来计算被测容器 中流体的压力。U型管内装有重度 大于被测流体重度的液体工作介质， 如水、酒精、四氯化碳和水银等。 它是根据被测流体的性质、被测压 力的大小和测量精度等来选择的。
注意
等压面的性质适用于同种连续的静止流体
2
2'
1
1'
不连续
流体种类不同
第三节 压强的计算基准和度量单位
一、压强的计算基准
a.绝对压强：是以绝对真空状态下的压强（绝对零压强） 为基准计量的压强。
b.相对压强：又称“表压强”，是以当地工程大气压(at) 为基准计量的压强。相对压强可“＋”可“– ”，也可为 “0”。
第二章 流体静力学
第一节 流体静压强及其特性 第二节 重力场中流体的平衡 第三节 压强的计算基准和度量单位 第四节 液柱测压计 第五节 静止流体作用在固体壁面上的总压力 第六节 液体平衡微分方程 第七节 液体的相对平衡
第一节 流体静压强及其特性
一.流体静压强的定义
面积ΔA上的平均流体静压强P：
P P A
2.几何意义：
位置水头z ：任一点在基准面0-0以上的位置高度，
表示单位重量流体从某一基准面算起所具有的位置
势能，简称位能。
测压管高度
P g
：表示在压强作用下沿测压管上升的
高度。
测压管水头（
Z＋
P g
）：测压管水面相对于基准面的高
度。
三.等压面
1.定义：静压强相等的点组成的面。
2.特性：
1）在平衡液体中，等压面与质量力的合力垂直。 2）等压面不能相交。 3）静止、同种、连续的液体中，水平面是等压面。
如果测量较小的液体压力差时， 也可以采用倒置式U型管差压计。 如果被测量的流体的压力差较大， 则可采用双U型管或多U型管差压 计。
当测量很微小的流体压力时，为了提高测量精度，常常 采用斜管微压计。斜管微压计的结构如图2-16所示。 它是由一个大容器连接一个可以调整倾斜角度的细玻璃 管组成，其中盛有重度为γ的工作液体。
在测压前，斜管微压计的两端与大气相通，容器与斜管内的 液面平齐(如图中的0-0断面)。
ppahpa (h1h2)
常用换算关系：
1atm=1.03323at=101325Pa=1.01325bar=760m mHg=10332.3mmH2O 1at=98070Pa=10000mmH2O=735.6mmHg
第四节 液柱测压计
一、测压管
测压管：是以液柱高度为表征测量 点压强的连通管。一端与被测点容 器壁的孔口相连，另一端直接 和 大气相通的直管。
整理 p2p1gh
液体静力学基本方程式为 pp0 gh
二.流体静力学基本方程的意义
1.A点的压强
p p 0g h p 0g (z 0 z )
整理
p
g
z
p0
gLeabharlann z0常数意义：
Z——单位重量液体的位置势能(简称比位能)；
—p—静止液体中单位质量液体的压力能(简称比压能)，
g
比位能与比压能之和称为总比能。
证明:从平衡状态下的流体中取一微元四面体 OABC，如图所示取坐标轴。
由于液体处于平衡状态，则有 为零，则：
，即各向分力投影之和亦
x方向受力分析: 表面力：
质量力：
当四面体无限地趋于O点时，则dx趋于0，所以有：px=p 类似地有：px=py=pz=pn
说明：
1. 静止流体中不同点的压强一般是不等的，一 点 的各向静压强大小相等。 2. 运动状态下的实际流体，流体层间若有相对运 动，则由于粘 性会产生切应力，这时同一点上各 向法应力不再相等。
3.运动流体是理想流体时，不会产生切应力，所以 理想流体动压强呈静水压强分布特性，即
第二节 重力场中流体的平衡
一.流体静压强的基本方程
静止液体所受的力除了液体重 力外，还有液面上的压力和固 体壁面作用在液体上的压力， 其受力情况如图所示。
1.受力平衡方程
p 2 A p 1 A g l A co 0 s
注意：工作介质与被测流体相互不能掺混。
A
h1
2
B
C
如果被测流体的压力较高，用一个U型管则较长，可以采用 串联U型管组成多U型管测压计。通常采用双U型管或三U型 管测压计。
三、差压计
U型管差压计用来测量两个容器或 同一容器(或管道等)流体中不同位 置两点的压力差。测量时，把U型 管两端分别和不同的压力测点A和B 相接，如图所示。
c.真空：是指绝对压强小于一个大气压的受压状态，是 负的相对压强。
正 压：相对压强为正值（压力表读数）。 负 压：相对压强为负值。 真空度：负压的绝对值(真空表读数，用Pv表示)。
p A
Pa A点绝对压强
0
A点相对压强
B点真空度 B
大气压强 Pa
B点绝对压强
绝对压强 0
二、压强的三种度量单位
a.应力单位
A 点 上 的 流 体 静 压 强 P： P LimP Aa A
二、流体静压强的特性
1、静压强的方向— 沿作用面的内法线方向
原因：静止流体表面应力只能是压应力或压强，且流体不能承 受拉力，且具有易流动性必须。
2、在静止流体内部，任一点的流体静压强的大小与作用面的方向 无关，只与该点的位置有关。
这是从压强定义出发，以单位面积上的作用力来表示 的，N/m2，Pa，kN/ m2 ，kPa。
b.大气压
标准大气压：1标准大气压(atm)=1.013X105Pa=101.3 kPa 工程大气压：at （1kgf/㎡）
c.液柱高度
水柱高mH20：1atm相当于 1at相当于
汞柱高mmHg：1 atm相当于 1at相当于