带符号数的表示
- 格式:ppt
- 大小:299.51 KB
- 文档页数:78


计算机中数的表⽰和存储(总结)⼀、⽆符号数和有符号数1.⽆符号数计算机中的数均存放在寄存器中,通常称寄存器的位数为机器字长。
所谓的⽆符号数即没有符号的数,在寄存器中的每⼀位均可⽤来存放数值。
⽽当存放有符号位时,则留出位置存放“符号”。
因此,在机器字长相同时,⽆符号数与有符号数所对应的数值范围是不同的。
以机器字长16位为例⼦,⽆符号数的范围为0~(216-1=65535),⽽有符号数的表⽰范围为(-32768=215)~(+32767=215-1)(此数值对应原码表⽰)。
机器中的有符号数是⽤补码表⽰的。
2.有符号数对于有符号数⽽⾔,符号的正负机器是⽆法识别的,⽽在机器中是⽤0,1分别表⽰正,负的,并规定将它放在有效数字的前⾯,这样就组成了有符号数。
把符号“数字化”的数叫做机器数,⽽把带“+”或“-”符号的数叫做真值。
⼀旦符号数字化后,符号和真值就形成了⼀种新的编码。
有符号数有原码、补码、反码和移码等四种表⽰形式。
2.1 有符号数的编码⽅法-原码表⽰法原码是机器数中最简单的⼀种表⽰形式,其符号位为0表⽰正数,为1表⽰负数,数值位即真值的绝对值,故原码⼜称作带符号位的绝对值表⽰。
整数原码的定义为式中x为真值,n为整数的位数。
例如,当x=-1110时,[x]原=24-(-1110)=11110⼩数的原码定义为例如,当x=-0.1101时,[x]原=1-(-0.1101)=1.1101当x=0时[+0.0000]原=0.0000[-0.0000]原=1-(0.0000)=1.0000可见[+0]原不等于[-0]原,即原码中的零有两种表⽰形式。
原码编码的优缺点其表⽰简单明了,易于和真值转换,但⽤原码进⾏加减运算时,确带来了许多⿇烦。
2.2 有符号数的编码⽅法-补码表⽰法补码利⽤了⽣活中的“补数”的概念,即以某个数为基准,称为模数,该数对模数的取模运算的结果就是补数。
例如,-3=+9(mod12),4=4(mod12)=16(mod12)。


简答题1.带符号的数在计算机中有哪些表示方法?特点如何?答:带符号的数在计算机中可以用原码、反码和补码表示。
采用原码和反码表示时,符号位不能同数值一道参加运算。
补码表示可以将减法运算转换为加法运算,同时数值连同符号位可以一起参加运算,这非常有利于计算机的实现。
2.单片机与其它常见微机(如PC机)有什么不同?它有什么独特优点?答:(1)主要有三点不同:一是CPU、存储器和I/O接口这几部分集成在一片芯片上;二是存储器设计采用了哈佛结构,将程序存储器和数据存储器在物理上分开;三是供位处理和位控制的资源丰富、I/O接口完善。
(2)优点:1)集成度高、价格低廉、性能/价格比高;2)程序存储器和数据存储器在物理上分开,可使程序不受干扰,抗干扰能力强;3)布尔处理能力强,适于工业控制。
3.堆栈区与一般的数据存储区有何异同?其重要作用是什么?答:堆栈区与一般存储区相同之处是:它们都属于存储器的一部分,都能存放数据。
其主要不同之处是对数据的存取规则有异:一般存储区使用随机读/写规则,而堆栈使用先进后出(或后进先出)规则。
堆栈采用这种特殊规则后,可以圆满完成子程序调用或中断调用,多级子程序嵌套等功能。
当然,堆栈区内的存储单元也可以使用随机读/写指令,但在这种情况下已经不把该单元当做堆栈看待了。
4.简述80C51单片机四个端口的带负载能力。
答:P0口的每一位口线可以驱动8个LSTTL负载。
在作为通用I/O口时,由于输出驱动电路是开漏方式,由集电极开路(OC门)电路或漏极开路电路驱动时需外接上拉电阻;当作为地址/数据总线使用时,口线输出不是开漏的,无须外接上拉电阻。
P1、P2、P3口的每一位能驱动4个LSTTL负载。
它们的输出驱动电路设有内部上拉电阻,所以可以方便地由集电极开路(OC门)电路或漏极开路电路所驱动,而无须外接上拉电阻。
5.MCS-51引线中有多少I/O引线?它们和单片机对外的地址总线和数据总线有什么关系?简述8031单片机中P0、P1、P2、P3口的主要作用。

为什么8位有符号数的范围是“-128 至+127”这是一个困惑了我几年的问题,它让我对现在的教科书和老师极其不满,从我N年前开始摸电脑时,就几乎在每一本C++教科书上都说,8 位有符号的取值范围是-128~+127,为什么不是-127~+127呢,后来的java,int 的聚值范围,再32 位计算,-2^31 ~ +2^31-1,可是,却从来没有任何一本教科书或一个老师比我解释过这个问题。
原因没有在工作上或者是什么地方直接遇到它,所以我也一直忽略它,但心里总是有一根刺.直到刚才就是刚才,无聊之极,在看汇编的书时,又遇到它了,但一如以往,书上直接地,有心地,明显地绕过了这个问题,真是可恶啊.几经周折,终于把它搞清楚了:其实它是计算机底层为了实现数值运算而决定的,涉及非常基础的源码,反码,补码知识,一般用不上,但是计算机考试除外。
用2^8来表示无符号整数的话,全世界的理解都是0 - 255了,那么,有符号呢? 用最高位表示符号,0 为+,1 为-,那么,正常的理解就是-127 至+127 了.这就是原码了,值得一提的是,原码的弱点,有2 个0,即+0 和-0,还有就是,进行异号相加或同号相减时,比较笨蛋,先要判断2个数的绝对值大小,然后进行加减操作, 最后运算结果的符号还要与大的符号相同.于是乎,反码产生了,原因....略,反正,没过多久,反码就成为了过滤产物,也就是,后来补码出现了.补码的知识不说述,只说有关+127 和-128 的.官方的定义[-2^(n-1),2(n-1)-1],补码的0 没有正负之分.原因呢?没有一本书上有说,这也是我这么火的原因,但通过思考,google,再思考,很快找到答案:首先,难不免干点白痴般地事情,穷举一下...正数,原码跟补码一样+127, 0111 1111+126, 0111 1110+125, 0111 1101+124, 0111 1100+123, 0111 1011+122, 0111 1010...+4, 0000 0100+3, 0000 0011+2, 0000 0010+1, 0000 00010, 0000 0000 (无正负之分)下面是负数了,值,原码,符号位不变其它取反,+1-1, 1000 0001, 1111 1110, 1111 1111-3, 1000 0011, 1111 1100, 1111 1101-4, 1000 0100, 1111 1011, 1111 1100-5, 1000 0101, 1111 1010, 1111 1011-6, 1000 0110, 1111 1001, 1111 1010-7, 1000 0111, 1111 1000, 1111 1001-8, 1000 1000, 1111 0111, 1111 1000-9, 1000 1001, 1111 0110, 1111 0111-10, 1000 1010, 1111 0101, 1111 0110-11, 1000 1011, 1111 0100, 1111 0101-12, 1000 1100, 1111 0011, 1111 0100-13, 1000 1101, 1111 0010, 1111 0011-14, 1000 1110, 1111 0001, 1111 0010-15, 1000 1111, 1111 0000, 1111 0001-16, 1001 0000, 1110 1111, 1111 0000-17, 1001 0001, 1110 1110, 1110 1111...-24, 1001 1000, 1110 0111, 1110 1000...-99, 1110 0011, 1001 1100, 1110 0100...-124, 1111 1100, 1000 0011, 1000 0100-125, 1111 1101, 1000 0010, 1000 0011-126, 1111 1110, 1000 0001, 1000 0010-127, 1111 1111, 1000 0000, 1000 0001看出点什么了没有?如果没有,那么,给个提示, 再继续下去,下一个补码是什么呢?当然是-128, 先略过,再略过, 1000 0000-127 补码是1000 0001 还可以在减去1 1000 0000 -1281000 0000,那么,它的原码是什么呢?从补码求原码的方法跟原码求补码是一样的先保留符号位其它求反: 1111 1111, 再加1:11000 0000, 超过了8 位了对,用8 位数的原码在这里已经无法表示了关键就在这里,补码1000 0000 为-128 是不用怀疑的(上面的穷举),那么,回到原码处, 它的原码也是1000 0000(超出的自动丢失),1000 0000 在原码表示什么呢? -0, 但补码却规定0 没有正负之分转换一下思路,看看计算机里,是怎么运算的:对于负数,先取绝对值,然后求反,加一-128 -> 128 -> 1000 0000 -> 0111 1111 -> 1000 0000现在明确了吧.所以, 8 位有符号的整数取值范围的补码表示1000 0000 到0000 0000, 再到0111 1111即-128 到0, 再到127最终-128 ~ +127-------------------------完------------------------。
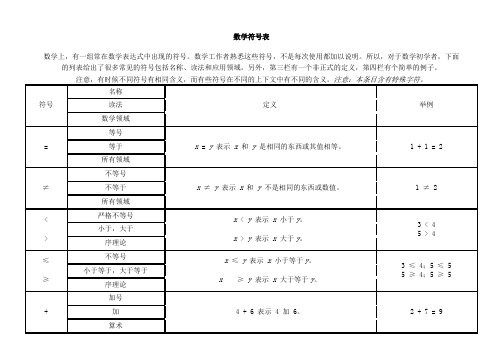
数学符号表
数学上,有一组常在数学表达式中出现的符号。
数学工作者熟悉这些符号,不是每次使用都加以说明。
所以,对于数学初学者,下面的列表给出了很多常见的符号包括名称、读法和应用领域。
另外,第三栏有一个非正式的定义,第四栏有个简单的例子。
补充说明
然而原表中虽然有六十余个符号,却对初等数学的符号尚未罗列完整,随便点出几处:
原表
有阶乘符号而无排列组合符号;
有函数符号而无反函数符号;
有代数符号而基本无几何、三角、反三角符号(仅有一个垂直符号);
有平方根符号而无立方根、n次方根符号;
有导数符号而无极限符号;
有等于符号而无恒等于、同余符号;
有向量叉乘符号而无有向线段、向量、向量数量乘积(点乘积)符号;
有复数绝对值(应为模)符号而无复数、共轭复数、复数实虚部符号;
无对数符号、指数符号
对于高等数学,表中所列符号仅占全部符号的1/3。
另外表中所列符号还有错误和赘疣:
符号| | :对实数是绝对值,对复数是模(尤其对虚数);
符号Φ:表示空集,空集不是用{ } 表示;
符号≌:几何中表示全等,近世代数(群论)中表示同构,同构不是用≈号;
符号-:集合论中的补集,这在过去是对的,但现在集合论中的补集已不是这个符号,
复合函数符号没有省去或简化任何一个字符,反而多出一个赘疣,有悖定义符号的原则,不知是哪位教授独创?符号规定应有部颁标准,当然也符合绝大多数数学工作者的习惯,少数独创的应不在此列。
物理符号大全注:由于符号中特殊符号无法在此编辑器中显示,因此对于这部分符号只能用文字描述。
一、数学符号1. $\alpha$,$\beta$,$\gamma$:希腊字母,通常用于表示角度、系数等。
2. $\theta$:希腊字母,通常用于表示角度。
3. $\pi$:希腊字母,代表圆周率。
4. $\infty$:无限大,表示数列或函数趋于无限大。
5. $\pm$:加减号,表示正数或负数。
6. $\times$:乘号,表示两个数相乘。
7. $\div$:除号,表示一个数除以另一个数。
8. $\sqrt{a}$:平方根,表示一个数的平方根。
9. $a^n$:指数,表示一个数的n次方。
10. $log_a{b}$:对数,表示以a为底b的对数。
11. $\sum$:求和符号,表示将一列数相加。
12. $\prod$:乘积符号,表示将一列数相乘。
13. $<$,$>$:大于号和小于号,表示大小关系。
14. $\leq$,$\geq$:小于等于号和大于等于号,表示大小关系。
15. $=$:等于号,表示两个数相等。
16. $\neq$:不等于号,表示两个数不相等。
17. $\approx$:约等于号,表示两个数近似相等。
18. $\in$:属于,表示一个数属于某个集合。
19. $\notin$:不属于,表示一个数不属于某个集合。
20. $\mid$:竖线,表示除法的分数线,或表示绝对值。
21. $\rightarrow$:箭头,表示方向。
22. $\leftrightarrow$:双向箭头,表示两个方向。
二、物理符号23. $E$:能量,单位为焦耳。
24. $m$:质量,单位为千克。
25. $v$:速度,单位为米/秒。
26. $a$:加速度,单位为米/秒^2。
27. $q$:电荷量,单位为库仑。
28. $G$:万有引力常数,单位为牛顿·米^2/千克^2。
29. $F$:力的大小,单位为牛顿。
标题:16bit带符号数的16进制表示1. 前言16bit带符号数是在计算机科学中常见的数据类型之一。
它可以表示范围广泛的数值,包括正数、负数和零。
在进行数据处理和存储时,我们经常需要将这些数值转换成不同的表示方式,其中包括16进制表示。
本文将讨论16bit带符号数的16进制表示方法,以及相关的计算和应用。
2. 16bit带符号数的定义在计算机中,16bit带符号数是指由16个二进制位组成的数据类型,其中一位用来表示符号位(0表示正数,1表示负数),其余15位用来表示数值。
它的取值范围为-xxx到xxx。
在不同的编程语言和评台中,对于16bit带符号数的表示方式可能有所不同,但其基本概念是一致的。
3. 16进制表示方法将16bit带符号数转换成16进制表示可以简化数据的存储和处理。
在进行转换时,首先需要将数值转换成二进制形式,然后再根据一定的规则将二进制数值转换成16进制表示。
以下是16bit带符号数转换成16进制表示的步骤:3.1 将十进制数值转换成二进制形式对于正数,直接将其转换成二进制形式即可;对于负数,则需要先将其绝对值转换成二进制形式,然后取反加一得到补码表示。
十进制数-10对应的二进制表示为xxx。
3.2 将二进制数值分割成四位一组将得到的二进制数值分割成四位一组,不足四位的在前面补0。
xxx可以分割为1111和0110。
3.3 将每组二进制数值转换成对应的16进制表示将每组四位二进制数值转换成对应的16进制表示。
1111对应的16进制表示为F,0110对应的16进制表示为6。
3.4 合并各组16进制数值将得到的各组16进制数值合并在一起,得到最终的16进制表示。
-10的16进制表示为F6。
4. 计算示例为了更好地理解16bit带符号数的16进制表示方法,我们可以通过一个具体的计算示例来加深印象。
假设我们需要将十进制数-xxx转换成16进制表示,我们可以按照上述步骤进行计算:1. 将-xxx转换成二进制形式-xxx的绝对值为xxx,它的二进制表示为xxx。
11以上的数学符号
1. 大于号(>),表示一个数大于另一个数,例如,5 > 3。
2. 小于号(<),表示一个数小于另一个数,例如,2 < 7。
3. 大于等于号(≥),表示一个数大于或等于另一个数,例如,
4 ≥ 4。
4. 小于等于号(≤),表示一个数小于或等于另一个数,例如,9 ≤ 10。
5. 不等于号(≠),表示两个数不相等,例如,6 ≠ 8。
6. 等于号(=),表示两个数相等,例如,3 + 2 = 5。
7. 加号(+),表示两个数相加,例如,2 + 4 = 6。
8. 减号(-),表示两个数相减,例如,8 3 = 5。
9. 乘号(×),表示两个数相乘,例如,3 × 7 = 21。
10. 除号(÷),表示一个数除以另一个数,例如,10 ÷ 2 = 5。
11. 等于或大于号(≥),表示一个数等于或大于另一个数,例如,7 ≥ 5。
12. 等于或小于号(≤),表示一个数等于或小于另一个数,例如,4 ≤ 6。
这些符号在数学中被广泛应用,用于表示数学关系、运算和比较。
希望这些信息能够帮助到你理解11以上的数学符号。