附录F：结构基本自振周期的经验公式

结构自振周期计算公式结构自振是指结构体因受力作用，而发生固有频率的振动，是工程结构设计过程中的重要因素之一，其自振周期的计算也是工程分析与设计的重要参考。

一、结构自振周期计算的基本原理结构自振周期表示在定荷载作用下，结构体内存在的固有振动频率，而在房屋建筑等结构设计中，计算结构的自振周期可以给予工程师指导性的数据，从而判断结构的稳定性以及进行优化设计。

在分析自振周期时，振动方程为：$Mfrac{d^2u}{dt^2}+Ku=Fsin(wt)$其中：$M$为质量；$K$是刚度；$F$为外力；$w$为频率；$t$为时间。

由上述振动方程可推知，均布荷载情况下，自振周期可表示为： $T=2pisqrt{frac{M}{K}}$二、基于结构自振周期计算的工程实践1.建筑结构目前，建筑结构自振周期的计算方法多以勒温斯顿公式为指导，该公式如下：$T=2pisqrt{frac{mh}{3K}}$其中，$m$为梁或柱的质量，$h$为梁或柱的高度，而$K$为梁或柱的刚度。

由此可知，在建筑结构设计中，如果要实现某一特定的自振周期，就可以根据公式的参数来准确计算出梁或柱的质量和高度，进而实现设计要求。

2.机械结构在机械结构设计中，自振周期计算常用结构动力学公式：$T=2pisqrt{frac{J}{K}}$其中，$J$为动力学惯性矩，$K$为刚度。

由此可知，机械结构中要实现某一特定的自振周期，可以根据公式参数来计算动力学惯性矩和刚度，然后以计算结果为指导，从而实现设计要求。

三、结构自振周期计算的工程应用1.减小建筑物抗震性能近年来，随着自然灾害的增多，设计出具有良好抗震性能的建筑结构越来越受到重视，而结构自振周期的计算可以指导工程师控制结构的振动，从而减少结构层受到的震力，减少损坏层的概率，提高其受震抗力。

2.提高机械设备的耐久性耐久性是指机械设备承受外力时对结构持续不变的能力，而机械设备的自振周期可以提高设备的耐久性，使其可以承受外力的一定频率振动，从而提高设备的维护效率，延长其使用寿命。

附录F 结构基本自振周期的经验公式F.1 高耸结构F.1.1 一般高耸结构的基本自振周期，钢结构可取下式计算的较大值，钢筋混凝土结构可取下式计算的较小值：H T )013.0～007.0(1= (F.1.1)式中：H ——结构的高度(m)。

F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用：1，烟囱的基本自振周期可按下列规定计算：1)高度不超过60m 的砖烟囱的基本自振周期按下式计算：dH T 2211022.023.0-⨯+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211010.041.0-⨯+= (F.1.2-2) 3)高度超过150m ，但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211008.053.0-⨯+= (F.1.2-3) 式中：H ——烟囱高度(m)；d ——烟囱1/2高度处的外径(m)。

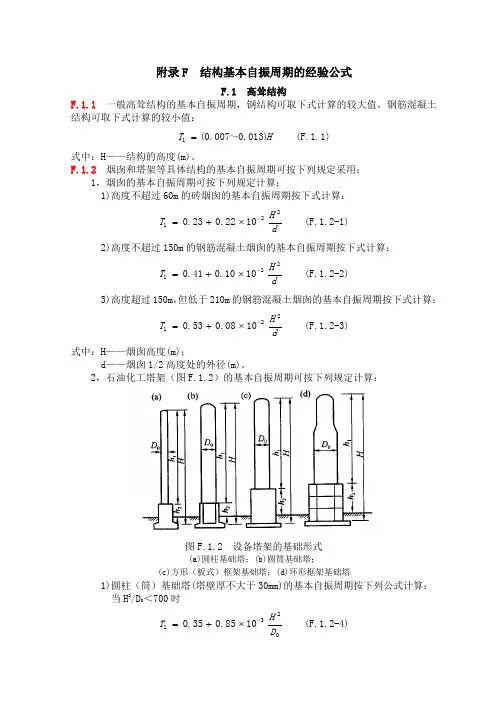
2，石油化工塔架（图F.1.2）的基本自振周期可按下列规定计算：图F.1.2 设备塔架的基础形式(a)圆柱基础塔；(b)圆筒基础塔；(c)方形（板式）框架基础塔；(d)环形框架基础塔1)圆柱（筒）基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算： 当H 2/D 0＜700时2311085.035.0D H T -⨯+= (F.1.2-4)当H 2/D 0≥700时2311099.025.0D H T -⨯+= (F.1.2-5) 式中：H ——从基础底板或柱基顶面至设备塔顶面的总高度(m)；D 0——设备塔的外径(m)；对变直径塔，可按各段高度为权，取外径的加权平均值。

2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算：2311040.056.0D H T -⨯+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。

4)当若干塔由平台连成一排时，垂直于排列方向的各塔基本自振周期T 1可采用主塔（即周期最长的塔）的基本自振周期值；平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。

混凝土结构的自振频率计算方法混凝土结构的自振频率计算方法1. 引言混凝土结构是现代建筑工程中常用的结构形式之一，具有良好的耐久性和承载能力。

在设计和施工过程中，了解混凝土结构的自振频率是至关重要的。

自振频率描述了结构在受到外力激励时产生共振的能力，对结构的稳定性和安全性有很大影响。

本文将介绍混凝土结构的自振频率计算方法。

2. 自振频率的定义自振频率是结构在无外力作用下自由振动的频率，它是由结构的固有特性决定的。

在混凝土结构中，自振频率可以反映结构刚度和质量分布的特点。

3. 自振频率的计算方法混凝土结构的自振频率可以通过多种方法进行计算，如理论计算、实测和数值模拟等。

以下将介绍常用的理论计算方法。

3.1 欧拉-伯努利梁理论欧拉-伯努利梁理论是一种常用的计算混凝土梁自振频率的方法。

根据该理论，混凝土梁的自振频率可以通过以下公式计算：f = (π^2 * E * I) / (L^2 * ρ)其中，f是自振频率，E是混凝土的弹性模量，I是截面的惯性矩，L是梁的长度，ρ是混凝土的密度。

3.2 有限元法有限元法是一种常用的对复杂结构进行自振频率计算的数值模拟方法。

该方法将结构离散化为有限个小单元，通过求解单元之间的振动方程来计算结构的自振频率。

有限元法可以考虑结构的非线性和非均匀性，具有较高的精度和适用性。

4. 自振频率计算的影响因素混凝土结构的自振频率受多种因素的影响，包括结构的几何形状、材料性质、边界条件等。

以下将介绍几个常见的影响因素。

4.1 结构的几何形状结构的几何形状是决定自振频率的重要因素之一。

通常情况下，结构的自振频率与结构的尺寸成反比关系。

横截面更大的梁具有更低的自振频率。

4.2 材料的性质混凝土的弹性模量和密度是决定自振频率的关键参数。

较高的弹性模量和较低的密度将导致较高的自振频率。

4.3 边界条件结构的边界条件也会对自振频率产生影响。

不同的边界条件将导致不同的结构振型和自振频率。

受到固定边界约束的结构具有更高的自振频率。

附录F 结构基本自振周期的经验公式F.1 高耸结构F.1.1 一般高耸结构的基本自振周期，钢结构可取下式计算的较大值，钢筋混凝土结构可取下式计算的较小值：H T )013.0～007.0(1= (F.1.1)式中：H ——结构的高度(m)。

F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用：1，烟囱的基本自振周期可按下列规定计算：1)高度不超过60m 的砖烟囱的基本自振周期按下式计算：dH T 2211022.023.0-⨯+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211010.041.0-⨯+= (F.1.2-2) 3)高度超过150m ，但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211008.053.0-⨯+= (F.1.2-3) 式中：H ——烟囱高度(m)；d ——烟囱1/2高度处的外径(m)。

2，石油化工塔架（图F.1.2）的基本自振周期可按下列规定计算：图F.1.2 设备塔架的基础形式(a)圆柱基础塔；(b)圆筒基础塔；(c)方形（板式）框架基础塔；(d)环形框架基础塔1)圆柱（筒）基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算： 当H 2/D 0＜700时2311085.035.0D H T -⨯+= (F.1.2-4)当H 2/D 0≥700时2311099.025.0D H T -⨯+= (F.1.2-5) 式中：H ——从基础底板或柱基顶面至设备塔顶面的总高度(m)；D 0——设备塔的外径(m)；对变直径塔，可按各段高度为权，取外径的加权平均值。

2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算：2311040.056.0D H T -⨯+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。

4)当若干塔由平台连成一排时，垂直于排列方向的各塔基本自振周期T 1可采用主塔（即周期最长的塔）的基本自振周期值；平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。