随机振动系统的建模与分析

随机振动分析报告1. 引言随机振动是振动工程中的重要研究领域，对于各种结构和系统的设计与分析都具有重要的意义。

本文将介绍随机振动分析的基本概念、方法和步骤，并通过一个示例来说明如何进行随机振动分析。

2. 随机振动的基本概念随机振动是指在一定时间范围内，振动信号的幅值和频率是不确定的、随机变化的。

随机振动的特点是无法通过确定性的数学模型来描述，因此需要采用统计方法进行分析。

3. 随机振动分析的步骤随机振动分析的基本步骤包括：信号采集、数据预处理、频谱分析、统计分析和模型建立等。

3.1 信号采集随机振动信号的采集可以通过传感器等设备进行。

采集到的信号需要进行滤波和采样处理，以便后续分析。

3.2 数据预处理在进行频谱分析和统计分析之前，需要对采集到的数据进行预处理。

常见的预处理方法包括去除噪声、补充缺失数据和归一化处理等。

3.3 频谱分析频谱分析是对随机振动信号进行频域分析的方法。

通过对信号的频谱特性进行分析，可以了解信号的频率分布和主要频率成分。

3.4 统计分析统计分析是对随机振动信号进行统计学特征分析的方法。

常见的统计分析方法包括均值、方差、自相关函数和互相关函数等。

3.5 模型建立通过对随机振动信号的分析，可以建立相应的数学模型，用于预测和仿真。

常见的模型包括自回归模型和自回归移动平均模型等。

4. 示例：汽车发动机的随机振动分析以汽车发动机的随机振动分析为例，介绍随机振动分析的具体步骤。

4.1 信号采集使用加速度传感器对汽车发动机进行振动信号的采集。

将传感器安装在发动机的合适位置，以获取准确的振动信号。

4.2 数据预处理对采集到的振动信号进行滤波和采样处理，去除噪声和不必要的频率成分，并将信号进行归一化处理。

4.3 频谱分析将预处理后的振动信号进行频谱分析，得到信号的频谱特性。

可以使用FFT算法将信号从时域转换为频域，并绘制频谱图。

4.4 统计分析对频谱分析得到的数据进行统计分析，计算信号的均值、方差和自相关函数等统计学特征。

振动系统的建模与分析方法振动是一种普遍存在的现象，在机械系统、建筑物、车辆等各方面都有应用。

因此，掌握振动系统的建模和分析方法对于工程领域的研究和设计是至关重要的。

一、振动系统的建模振动系统通常可以看作是由质量、弹性元件和阻尼元件组成的。

其中质量是指系统中的物体，弹性元件是指连接在物体之间的弹簧和弹性杆件，阻尼元件是指连接在物体和外界之间的摩擦力和粘滞力。

建立振动系统的数学模型时，需要考虑物体的运动规律和系统的动态特征。

一般来说，可以采用以下方法：1. 基于质量-弹簧-阻尼模型的分析在质量-弹簧-阻尼模型中，物体的质量被假设为一定量级的点质量，其固定在刚性平台上。

系统的弹簧元件通过牛顿第二定律可以表示为受力平衡问题。

阻尼元件采用线性或非线性模型，考虑阻尼对系统的影响。

2. 基于受力平衡方程的分析在受力平衡方程模型中，物体的质量、弹簧和阻尼元件被视为连续的弹性体。

通过对物体的运动和弹性体的受力平衡方程建模，可以得到系统的动态特性。

二、振动系统的分析方法振动系统的分析方法主要包括两种：频域分析和时域分析。

1. 频域分析频域分析是通过将物体的运动分解为不同的频率分量来描述系统的振动。

这种方法通常使用傅里叶变换对系统的运动进行分析。

傅里叶变换将系统的运动分解为周期分量，并以数学方式表示系统的频率响应。

2. 时域分析时域分析是直接对物体的运动进行分析，描述物体的运动随时间的变化。

这种方法主要使用微分方程和积分方程来表示系统的动态特性。

通常使用有限元法和数值时程法来计算系统的响应，以确定系统的稳定性和同步特性。

三、实际应用振动系统的建模和分析方法在许多工程领域中得到了广泛的应用。

例如，研究机械系统的振动特性可以为机械设计和优化提供支持。

在建筑物和桥梁的振动分析中，可以评估建筑物对地震、风力和交通运输的响应。

此外，振动模型也被应用于医学、声学、航空航天等领域。

总的来说，振动系统的建模和分析方法是工程领域中非常重要的一部分。

振动传感器性能测试及振动测试系统建模与性能分析实验一、 实验目的1. 了解各类型振动传感器的工作原理、掌握压阻式加速度传感器的动态校准过程。

2. 掌握正弦、随机振动控制的基本过程，能够根据实际情况合理设计校准过程中的参考谱。

3. 掌握振动传感器的动态校准方法并能计算出振动传感器的各项动态特性指标。

4. 了解振动测试系统的组成，掌握振动测试系统的建模方法5. 对于测试后未达到设计指标的系统，应当能够设计出动态补偿滤波器以补偿系统的动态特性。

二、实验系统组成振动测试系统由两部分组成，一部分是振动控制系统，另外一部分就是远程数据采集、处理系统。

实验系统中，振动控制系统的振动台按照预先设定的参考谱进行振动。

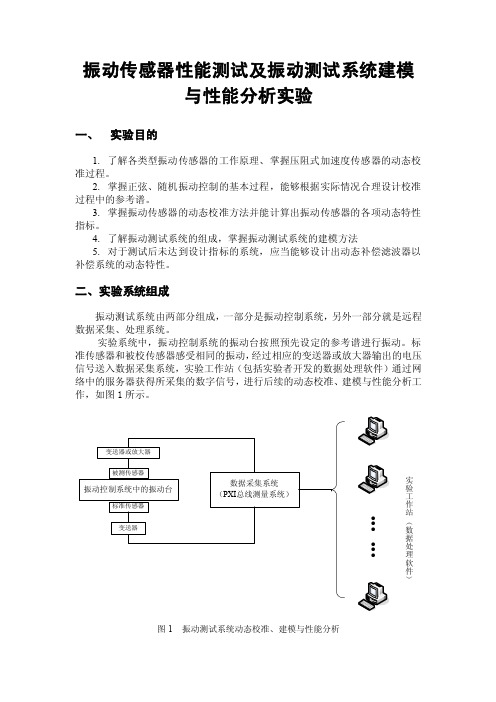
标准传感器和被校传感器感受相同的振动，经过相应的变送器或放大器输出的电压信号送入数据采集系统，实验工作站（包括实验者开发的数据处理软件）通过网络中的服务器获得所采集的数字信号，进行后续的动态校准、建模与性能分析工作，如图1所示。

● ● ● ● ●●实验工作站（数据处理软件）图1 振动测试系统动态校准、建模与性能分析三、实验系统工作原理1、振动控制系统工作原理振动控制系统中的振动台产生动态校准、动态测试所需的标准振动信号。

振动控制系统由振动控制仪、功率放大器、振动台和反馈传感器构成，目的是使振动台按照预先设定的参考谱进行振动。

振动控制仪安装在工控机中，振动控制信号从工控机发出，经过功率放大器对控制信号进行放大，驱动振动台振动。

而振动台的振动情况由安装在台面中心的反馈传感器获取，经过电荷放大器传送至工控机中的振动控制仪，从而形成闭环控制使振动台能够按照设定参考谱进行振动。

在振动台的夹具台面上采用背靠背方式安装标准传感器与被校传感器，这样保证了它们感受的是相同的振动信号，通过采集两个传感器的输出并将其送入实验工作站，参与实验的人员就可以在远程计算机上进行振动传感器的校准、建模及性能分析了。

2 数据采集系统工作原理数据采集系统配有NI公司的数字化仪（PXI－5122），可以实现双通道信号的同步采样。

随机振动力学模型研究及应用随机振动力学是一种探索物体在随机外力作用下的运动规律的学科，在现代科学技术中得到了广泛的应用。

该领域的研究往往需要通过数学模型来描述物体的振动特性，以实现对物体在复杂环境中的运动行为的预测和控制。

因此，随机振动力学模型的研究成为了该领域的一个重要研究方向。

随机振动力学模型的研究中，主要包括如下内容：1. 随机振动分析方法随机振动分析方法指的是对不确定性、复杂性、非线性的振动系统进行分析和计算的数学方法。

传统的振动分析方法是基于确定性原理，其中所采用的物理参数基本是确定值，但是当系统遇到外部的随机激励时，传统的振动分析方法会出现一些不足之处。

随机振动分析方法将随机力学原理引入到振动分析中，以描述复杂的随机振动系统。

随机振动分析方法包括稳态响应分析、瞬态响应分析、随机响应分析等等。

2. 随机振动系统建模建立随机振动系统模型的目的在于对所研究的随机振动系统进行定量分析和控制，依据研究的目的和实际需求，可以不同的方法和技术来进行建模。

建模的过程中，要综合考虑所研究的物理系统的具体特性，如物理结构、材料等方面，同时要结合所需求的研究结果来进行系统的建模。

基于随机振动理论，随机振动系统建模的核心在于对随机力、随机参数和随机噪声等因素进行分析和描述。

3. 随机振动控制研究随着现代技术的发展，随机振动控制研究变得越来越重要。

随机振动控制是通过适当的控制策略来降低、抑制随机振动和噪声的变化，使系统更加稳定的过程。

在随机振动控制研究中，智能材料和智能结构的出现，为实现振动控制提供了更多的手段和途径。

随机振动控制研究含有多学科的交叉，如力学、电气、控制等各学科，需要多学科的共同研究。

4. 随机振动分析与应用随机振动分析与应用是对随机振动理论的有效应用，可以应用于多个系统，如机械系统、电力系统等。

在应用研究中，通常建立相应的数学模型，来实现对所研究系统的分析、预测、控制等目的。

随着现代工业的发展，随机振动分析和应用得到了广泛的应用，如在机械领域中，可以通过对叶片的随机振动进行分析和控制，提高机械设备的可靠性和性能，为工业生产的发展做出了重要贡献。

电子设备的随机振动仿真分析随机振动是电子设备设计中一个重要的研究内容。

在实际工作环境下，电子设备常常会受到来自各种不同源头的随机振动的影响，这些振动有可能引发设备故障，或者对设备的正常运行产生不利影响。

因此，通过随机振动仿真分析，可以对电子设备的设计和性能做出科学的评估和改进。

电子设备的随机振动主要来自于以下几个方面：一是机械振动，包括设备的工作环境中的交通和机械设备振动等；二是自然环境振动，如地震、风力等；三是人为振动，例如人员操作和设备运行等。

这些振动的频率、振幅和方向都可能对电子设备的正常运行和寿命产生影响。

随机振动仿真分析的基本原理是将各种振动信号进行转换和处理，以模拟出实际振动环境下的电子设备工作状态。

具体分为以下几个步骤：首先，需要对设备的振动环境进行调查和实测，获取振动信号的频率谱密度和功率谱密度等参数。

这些参数是随机振动仿真分析的基础。

其次，需要建立电子设备的结构模型，并对设备的响应进行建模。

模型的精确度和准确度将直接影响仿真分析的结果。

然后，利用数值计算方法，将振动信号和设备响应信号进行转换和计算。

常用的计算方法有有限元法和边界元法等。

这些方法可以有效地模拟设备在振动环境中的振动状态。

最后，通过分析和比较模拟结果，评估设备在随机振动环境下的工作状态和可靠性。

如果发现设备出现故障概率较大或者工作性能下降，可以提出相应的改进措施，从而提高设备的设计和可靠性。

随机振动仿真分析在电子设备设计和优化中具有重要的意义。

通过对不同振动环境下设备的仿真分析，可以帮助工程师了解设备在实际工作中存在的问题，发现潜在的故障点，并提出相应的改进方案，从而提高设备的可靠性和性能。

此外，随机振动仿真分析还可以用于设备的故障诊断和寿命预测，为设备的维护和保养提供理论依据。

综上所述，随机振动仿真分析在电子设备设计和优化中发挥着重要的作用。

通过对设备在不同振动环境下的仿真分析，可以提高设备的可靠性和性能，减少设备故障率，从而为电子设备的设计和运维提供科学依据。

机械工程中的随机振动分析方法摘要随机振动分析方法是机械工程领域中重要的分析方法之一。

本文通过分析机械系统中的随机振动问题，介绍了随机振动相关的概念和分析方法，包括概率分布、功率谱密度、相关函数、自相关函数等。

同时，本文还介绍了随机振动分析方法的具体应用，例如在机械系统的设计、运动控制、故障诊断和损伤检测中的应用。

通过本文的阅读，读者将了解到随机振动分析方法在机械工程中的应用，以及如何通过这些方法更好地解决机械系统中的随机振动问题。

1.引言机械系统中的随机振动问题是机械工程中常见的问题之一。

对于机械系统而言，振动是不可避免的，然而，振动如果过于剧烈或者频率过高，就会引起机械系统的不稳定甚至毁坏。

因此，机械工程师需要对机械系统中的随机振动进行分析和处理。

随机振动分析方法是一种重要的机械工程分析方法。

本文将通过分析机械系统中的随机振动问题，介绍随机振动相关的概念和分析方法，并且将展示如何通过这些分析方法更好地解决机械系统中的随机振动问题。

2.随机振动的概念随机振动是指振动信号在时间域和频率域上都是随机的。

在机械系统中产生随机振动的原因很多，例如系统的结构松散、摩擦、失衡等。

对于机械系统而言，随机振动是不稳定的，因此需要进行分析和处理。

在进行随机振动分析时，我们需要了解以下几个概念：概率分布：指在一定范围内，每个随机事件发生的可能性大小。

在随机振动分析中，常用的概率分布包括正态分布、均匀分布等。

功率谱密度：指一个信号在频率域上的能量分布。

功率谱密度可以通过傅里叶变换将信号从时间域转换到频率域上进行计算。

相关函数：指在时间域上两个信号之间的相关性。

相关函数可以用来描述振动信号的相似程度。

自相关函数：指一个信号与自己的相关性。

自相关函数可以用来描述信号的周期性和重复性。

3.随机振动分析方法3.1 概率分布分析法在机械系统中，常用的随机振动分析方法之一是概率分布分析法。

概率分布分析法通过对信号的统计特性进行分析，得出信号的概率分布。

随机振动分析报告一、引言随机振动是指在时间和频率上都是随机变化的振动现象。

在工程领域中，随机振动分析是至关重要的，它可以帮助我们了解结构在实际工作环境中受到的振动荷载和激励情况，从而评估结构的稳定性和安全性。

本报告旨在对某结构进行随机振动分析并提供相应的结果和结论。

二、分析方法为了进行随机振动分析，我们采用了常用的频域分析方法，包括功率谱密度分析和相关函数分析。

具体步骤如下：1.收集振动数据：我们在某结构特定位置安装了加速度传感器，记录了一段时间内的振动数据。

2.数据预处理：通过滤波、去噪等手段对原始数据进行预处理，排除噪声和干扰。

3.功率谱密度分析：利用傅里叶变换将时域数据转换为频域数据，并计算功率谱密度函数。

4.相关函数分析：计算振动信号的自相关函数和互相关函数，分析信号的相关性和共振情况。

三、结果分析基于以上分析方法，我们得到了如下结果：1.功率谱密度函数：根据振动数据的频谱分析，我们得到了结构在不同频率下的振动能量分布情况。

通过对功率谱密度函数的分析，我们可以确定结构的主要振动频率和振动幅度。

2.相关函数：通过计算振动信号的自相关函数和互相关函数，我们可以了解振动信号在时间上的延迟和相关性。

这有助于评估结构的动态响应和共振情况。

根据以上结果分析，我们得出以下结论：1.某结构在特定频率下存在较大的振动能量，可能需要进行结构优化或加固。

2.振动信号存在一定的相关性，可能受到外界激励的影响，需要进一步分析振动源。

四、结论基于我们的随机振动分析，我们对某结构的动态响应和共振情况有了更深入的了解。

我们提供了功率谱密度函数和相关函数分析结果，并得出相关结论。

这些结果对于结构的稳定性和安全性评估具有重要意义，有助于指导结构的设计和改进。

以上是本次随机振动分析报告的主要内容，通过频域分析方法，我们对某结构的振动特性进行了全面研究，并提供了相应的结果和结论。

随机振动分析是工程领域中重要的技术手段，对于保障结构的可靠性和安全性具有重要意义。

机械工程中的随机振动分析方法随机振动是机械工程中一个重要的研究领域，它涉及到许多工程实践的问题，如结构的疲劳分析、噪声控制、可靠性评估等。

随机振动的特点是具有不确定性和复杂性，因此需要采用适当的分析方法来研究和解决相关问题。

本文将从概述随机振动的基本概念开始，介绍机械工程中常用的随机振动分析方法，并以实例说明其应用。

1. 随机振动的基本概念随机振动是指既没有确定的激励频率，也没有确定的相位的振动。

它是由不同振动频率、不同相位、不同幅度的振动分量叠加而成的。

在机械工程中，随机振动可以由多种因素引起，如不均匀质量分布、不平衡力、外界激励等。

为了对随机振动进行分析和研究，需要从概率论和统计学的角度进行建模和分析。

2. 傅里叶分析法傅里叶分析是一种将信号分解成不同频率振动成分的数学方法。

在随机振动分析中，傅里叶分析适用于研究振动信号的频谱特性，如功率谱密度、相关函数等。

通过傅里叶变换，可以将时域信号转换为频域信号，并从中获取振动信号的频谱信息。

傅里叶分析法在机械工程中常用于研究结构的固有频率、谐响应和失稳问题。

3. 频域法频域法是一种利用频谱分析对随机振动进行研究的方法。

通过对振动信号进行傅里叶变换，可以将其转换为频谱图。

频谱图可以反映振动信号各频率分量的能量分布情况，从而帮助研究和评估结构的振动性能。

在机械工程中，频域法常用于分析噪声、谐振问题以及系统的传递特性等。

4. 时域法时域法是一种通过直接观察振动信号在时间上的变化来研究随机振动的方法。

通过对振动信号进行波形分析，可以获得信号的振幅、时域波形、峰值等信息。

时域法在机械工程中常用于分析振动信号的幅值、波形、包络线等特性，可用于检测故障、评估结构健康状况等。

5. 概率论和统计学方法概率论和统计学是对随机振动进行建模和分析的重要工具。

通过概率密度函数、累积分布函数、随机过程等统计学方法，可以对振动信号的统计特性进行描述和分析。

在机械工程中，概率论和统计学方法常用于研究结构的可靠性、寿命预测、疲劳分析等问题。

随机振动系统的随机响应分析及其优化设计随机振动系统是指系统的外部激励是以随机波形出现的振动系统。

例如，一座大桥被风力或行车引起的震动，飞机在空气中运动时引起的振动等。

在实际工程结构中，许多振动系统都存在着随机激励，因此需要对系统进行随机响应分析。

随机振动系统的响应值是一个随机变量，因此它不能用一个确定的数值来描述。

为了对这种情况进行分析，我们需要用到概率论和统计学的知识。

随机激励的分布很复杂，常常假设为高斯分布。

高斯分布的随机变量的概率密度函数可以用以下公式表示：$$ f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$其中 $\mu$ 是均值，$\sigma$ 是标准差。

在振动系统中，均值常常取为0，因为我们主要关心振动的强度而不是振动的方向。

标准差则是描述振幅大小的指标，常用于刻画振动系统的强度。

在进行随机响应分析之前，需要对系统进行建模。

一般需要用到有限元法等数学方法对系统进行数学描述。

建模的目的是为了将系统的振动行为转化为数学方程，方便我们进行分析。

在建立数学模型之后，可以根据随机激励的特点，通过数学方法求得随机响应的概率密度函数、方差、均值等数学参数。

这些参数反映了系统响应的大小、变化范围、稳定性等重要的特性。

通过分析这些参数，我们可以得到系统响应的概率分布情况，找到系统的主要响应模式，为系统的设计和优化提供依据。

针对特定的工程结构和设计要求，我们可以通过优化设计来降低系统的随机响应。

优化设计是指在满足特定要求的前提下，选择合适的参数和方案，使系统效能达到最佳。

根据不同的优化目标和约束条件，我们需要采用不同的优化方法和算法。

常用的优化方法包括单目标优化、多目标优化、遗传算法等。

单目标优化是指在满足一定的约束条件下，同时优化一个目标函数，例如最小化系统的响应值。

多目标优化则是优化多个目标函数，例如既要最小化系统的响应值，又要使系统的重量尽量轻。

随机振动的建模与分析在现代社会中，不同领域的结构物、器材和设备等都需要经常性地进行振动测试和分析。

振动是一种周期性的物理现象，它和时间、频率之间的关系相当重要。

在自然界中，振动是广泛存在的。

例如，地震、海啸、风暴等天气现象，以及汽车、火车、飞机等运输交通工具的振动等。

由于振动随机性较强，因此在振动测试和分析中需要进行建模和分析。

本文将会详细的介绍随机振动的建模和分析。

1. 振动的概念振动是由于物体在受到内部或外部的力作用下，发生周期性的物理现象。

振动的本质是在某个固定的频率下，物体不断地在正向和反向移动。

这种运动状态是由“波浪”式的形式来描述、计算和分析的。

在振动过程中，物体会经历充满动态的运动形式和运动状态的周期性运动。

2. 振动的形式振动可以分为自由振动和强迫振动。

自由振动是指物体在未受到任何外界的干扰下，自然地发生振动。

而强迫振动是指物体在受到外界的周期性干扰下，发生振动。

强迫振动又分为单频振动和多频振动。

在单频振动中，物体振荡的频率是一个固定的频率，而在多频振动中，物体振荡的频率会在一定的范围内进行变化。

3. 随机振动的概念在振动的建模和分析中，随机振动是一种重要的振动形式。

随机振动是指强迫振动中，振动信号的频率和幅度是随机变量的情况。

相对于确定性振动来讲，随机振动更加复杂和不确定。

不同领域的工程和科学中，随机振动都有着相当重要的应用。

4. 随机振动的建模在建立随机振动模型时，需要充分考虑振动系统各个组成部分的非线性、时变性等特征。

建模中也需要考虑到随机干扰（噪声）对系统的影响。

常用的建模方法有统计模型、物理模型和混合模型。

5. 随机振动的分析在进行随机振动分析时，需要进行一定的振动测试。

通常采用的分析方法有时间域分析、频域分析和统计分析等。

时间域分析主要是对信号进行时域处理，例如波形分析、相位分析。

频域分析是对信号进行频域转换，例如傅里叶变换、小波变换等。

统计分析是通过统计学方式来分析信号数据，例如均值、方差、相关系数等。

随机振动系统的建模与滤波分析随机振动系统是指场景中的振动信号具有不确定性的特点，它是生产、工厂、地震、交通等领域广泛存在的现象。

因此，如何对随机振动信号进行建模和分析已成为目前研究的热点之一。

本文将从随机振动系统的建模和滤波分析两个方面入手，介绍一些相关的理论、方法和应用。

随机振动系统的建模在建立随机振动系统模型时，我们需要先对振动信号的概率分布进行分析。

根据国际标准ISO 2631-1，人体承受的振动信号可分为下面4类：1. 震动：频率大于1Hz的低频振动；2. 冲击：幅值较大，时间较短的高频振动；3. 振动加速度：真正的随机振动；4. 震动速度：中高频振动。

一般情况下，我们使用线性随机振动系统模型，它是指固定质点在一定时间内的随机振动。

我们假设振动信号在时间上满足均值函数和自相关函数，其数学模型可以描述为：$$\ddot{x}(t)+2\zeta\omega_{n}\dot{x}(t)+\omega_{n}^{2}x(t)=\frac{1}{m}f(t)$$其中，$\ddot{x}(t)$为加速度，$\dot{x}(t)$为速度，$x(t)$为位移，$m$为质点的质量，$f(t)$为受力，$\zeta$为阻尼系数，$\omega_{n}$为系统的固有频率。

在实际应用中，我们通常采用基于傅里叶变换的频域方法对信号进行建模。

这种方法的核心思想是先将信号变换到频域，然后对频域特征进行分析和处理。

在频域中，振动信号的能量分布是不均匀的，我们需要对其进行过滤和平滑，常用的方法有高通、低通、带通和带阻滤波器。

随机振动系统的滤波分析随机振动信号的特点是在时间和频域上是随机的，因此在信号处理中需要使用一些统计学和概率学的方法。

在随机信号滤波中，常用的方法有线性平均、递推平均和中值滤波等。

其中，线性平均是指将一段时间内的信号取平均值，以减少信号中的噪声，它的原理是根据噪声的统计特性，噪声随机分布，取多次采样平均后，噪声将趋于零。

机械工程中的随机振动分析随机振动分析在机械工程领域中具有重要的应用价值。

随机振动是指在时间和频率上变化不规则、不可预测的振动信号。

相比于确定性振动，随机振动更具挑战性，因为它不遵循某种确定的规律。

因此，对于机械工程师而言，研究随机振动并预测其影响对于设计和维护结构件、设备和机械系统非常重要。

要进行随机振动分析，首先需要了解随机振动信号的特征。

随机振动信号是由许多频率和振幅不同的振动成分组成的。

这些成分通常受到外界因素的影响，例如气候、机械振动或电磁辐射等。

通过将随机振动信号转化为频域表示，我们可以获得总的振动能量随频率的分布，这有助于进一步分析和理解系统的振动特性。

在机械工程中，随机振动分析主要应用于以下几个方面：1. 结构动力学：结构的安全可靠性是机械工程设计的关键要素。

随机振动分析可以帮助工程师预测结构在不同工况下的振动行为，包括自然振动频率、模态和共振等。

通过模态分析，可以确定结构的固有频率和振型，从而避免共振现象对结构的破坏。

2. 振动控制：随机振动分析也广泛应用于机械系统的振动控制。

在很多实际应用中，机械系统的振动需要控制在一定范围内，以确保系统的正常运行和寿命。

通过分析系统的振动特性，工程师可以设计控制系统，采取相应的控制策略，抑制或消除振动。

3. 可靠性评估：在机械工程中，很多结构和设备需要在严苛的工况下工作，例如航空航天、能源等领域。

随机振动分析可以帮助评估系统的可靠性，预测系统在随机振动环境下的寿命和性能损失。

这对于选择合适的材料和设计参数以及制定维护计划都具有重要意义。

4. 噪声控制：随机振动信号通常与噪声相关，例如噪声源产生的振动、流体介质中的振动等。

在机械工程中，对于噪声的控制是非常重要的，因为噪声不仅会对人的健康和舒适产生负面影响，还会对机械设备和结构产生损坏和故障。

随机振动分析可以帮助工程师确定噪声源、噪声的传播途径和传播路径，并制定相应的控制策略。

综上所述，随机振动分析在机械工程中具有广泛的应用，涉及结构动力学、振动控制、可靠性评估和噪声控制等方面。

结构设计知识：结构设计中的随机振动分析随机振动分析是结构设计中的一项重要技术，它能够帮助工程师在设计过程中更准确地了解结构在复杂环境下的动态响应情况，从而制定更有效的维护和保养计划，提高结构的安全性和可靠性。

在本文中，我们将探讨随机振动分析的基本概念、方法和应用，希望能为有志于从事结构设计工作的读者提供一些有用的参考信息。

一、随机振动分析的基本概念随机振动是指结构在随机或不规则的外力作用下产生的振动，其特点是频率和振动方向随时变化，并且与外界环境的状态有关。

随机振动分析通过建立更真实、更全面的结构模型，考虑到外部环境的随机性因素，以及结构本身的随机性因素，实现了对结构振动响应的最优化仿真模拟。

随机振动分析还可以用于评估结构的寿命和可靠性，以及确定结构在不同环境下的最适使用条件。

二、随机振动分析的方法随机振动分析的方法通常分为四个步骤：建立分析模型、定义外界随机振动负荷、计算结构响应、对结果进行评估。

1.建立分析模型在建立结构分析模型时，需要考虑材料和结构的本质特性，确定机构的几何形状和尺寸，并确定结构响应的潜在机制。

通常，随机振动分析采用板壳、有限元等方法建立结构模型。

2.定义外界随机振动负荷外界随机振动负荷通常指地震、风力、水流、机械振动等对结构施加的随机振动荷载。

在真实的环境下，随机振动负荷的频率变化范围和负荷强度不断变化，因此在随机振动分析中需要定义随机振动负荷的统计特性和概率分布。

3.计算结构响应通过分析结构的响应，可以对其在外界随机振动下的抗震能力进行评估，包括动态应力、变形和位移等。

通常，随机振动分析采用动力学方法或振动分析方法进行计算。

在计算过程中，需要考虑各种不确定性因素，如材料性能、结构几何形状、环境随机变量等，以及一些特殊因素，如结构损伤、非线性特性等。

4.对结果进行评估最后，需要对计算结果进行评估，确定结构的强度和刚度、动态特性等参数，并评估结构在不同环境下的稳定性和可靠性。

ANSYS随机振动分析教程随机振动分析(PSD: Power Spectral Density)是一种分析结构在随机动力加载下的响应特性的方法。

它通常应用于评估结构在实际工作环境中的可靠性和耐久性。

在ANSYS中进行随机振动分析，可以帮助我们理解结构在随机加载下的响应特性，评估结构的可靠性，并优化结构以提高其性能。

下面是一个基于ANSYS的随机振动分析的教程，通过该教程，你可以学习如何进行随机振动分析并分析结果。

步骤1:设置工程环境首先，打开ANSYS软件，并创建一个新的工程。

选择适当的单位制和求解器(如Mechanical APDL)。

步骤2:定义结构模型在这个教程中，我们将使用一个简单的悬臂梁作为结构模型。

创建一个梁模型，定义边界条件和加载条件。

确保模型准确代表了你想要分析的实际结构。

步骤3:定义随机负载在随机振动分析中，我们需要定义随机负载。

常见的随机负载包括自然地震、风荷载、机械振动等。

在这个教程中，我们以自然地震为例进行分析。

在ANSYS中，我们可以通过定义Power Spectral Density (PSD)函数来表示随机负载。

PSD函数描述了随机振动的能量分布，并用频率域表征。

使用命令“PSDZONE”创建一个PSD区域，然后通过命令“PSDFCN”定义一个PSD函数，并将PSD函数分配给PSD区域。

例如，你可以使用如下命令定义一个具有特定频率和幅值的PSD函数: /PSDZONE,1,FREQUENCY,1,200,AMP,0.1/PSDFCN,1,PSD,1步骤4:随机分析设置在进行随机振动分析之前，我们需要进行一些设置。

首先，我们需要定义分析的频率范围和步长。

可以使用命令“FREQSEP”来定义频率范围和步长。

例如，你可以使用如下命令定义频率范围为1Hz到200Hz，步长为1Hz:/FREQSEP,1HZ,1接下来，我们需要定义求解器参数。

使用命令“MODAL”定义模态分析参数:/COMBINATION,PSD/PSD,1,UNDEF然后，定义DAREA区域，并通过命令“SDPOINT”为每个频率分配一个积木节点。

随机振动控制及建模技术研究随机振动控制是振动控制中的一大类，它主要针对的是随机振动，也就是一种没有明确谱线的振动情况。

实际生活中，随机振动是十分普遍的，因此研究随机振动控制技术的重要性不言而喻。

本文将围绕随机振动控制展开探讨，探究其控制原理、建模技术及应用实例，为广大读者提供一些有用的知识和参考。

一、随机振动控制的控制原理随机振动的特点是是其振动信号不明显，没有明确的频率组分。

因此，随机振动控制的控制原理就是通过对随机振动的响应进行反馈控制，使系统在振动时能够保持较好的稳定性。

目前，随机振动控制的控制原理还存在许多问题需要进一步解决。

比如，如何建立与随机振动相适应的控制模型，如何选择合适的控制策略以及如何评估控制效果等。

二、随机振动控制的建模技术随机振动建模是控制随机振动的关键。

建模技术一般分为两类，一类是基于经验模型的建模方法，一类是基于物理模型的建模方法。

一般来说，基于经验模型的建模方法比较容易实现，但是建立的模型对于复杂的振动系统可能并不准确；而基于物理模型的建模方法虽然比较复杂，但是更加准确，能提供更多的控制方案。

三、随机振动控制的应用实例随机振动控制技术的应用范围十分广泛。

比如，在工业领域，机床的振动控制、风力发电机组的振动控制、地震安全设计以及船舶航行稳定性等方面都有着重要的应用；在科学研究中，随机振动控制也被广泛应用于无线通信、自动驾驶、智能家居等领域。

随机振动控制是振动控制领域中的一大难题，其控制原理和建模技术都需要进一步完善和优化。

但是，随着科学技术的不断发展，随机振动控制在工业生产和科学研究中的应用前景是十分广阔的。

作者希望借助本文，向广大读者介绍随机振动控制的基本知识，并为其今后的学习和研究提供一些参考。

结构随机振动仿真分析李如忠四川省绵阳市919信箱515分箱621900摘要利用Ansys有限元分析软件对某一安装架结构进行了动力学仿真分析，首先进行了模态分析，在此基础上进行了随机振动的PSD (Power Spectral Density)分析，通过分析，提出了结构的改进方案。

说明了在产品的设计过程中，对结构进行动力学仿真分析，可以预测产品的环境适应性，寻求最优化的设计方案，并缩短产品的开发周期，降低开发成本。

关键词有限元分析随机振动谱分析 PSDRandom vibration analysis of structureLi Ru-zhongP.O.Box 919-515, Mianyang, Sichuan 621900,CHINAAbstractThe dynamic simulation of a bracket structure is done via Ansys, a FEA(Finite Element Analysis) software program. First, the modal analysis is done, then the PSD(Power Spectral Density) analysis of random vibration is studied. The improved design is presented. The dynamic simulation plays an important role in product design cycle. It is helpful not only in seeking optimum solution for product, but also efficient in shortening the research cycle, reducing cost.Keywords FEA, random vibration, spectrum analysis, PSD1前言在电子产品的结构设计生产完成后，一般都要进行产品的随机振动试验，以检验其环境适应性。