希腊字母的不同意思
- 格式:doc
- 大小:12.15 KB
- 文档页数:1

delta数学符号
Delta是希腊字母Δ的名称,用作数学符号时表示差异、变化或增量。
在数学中,它可以表示许多不同的概念,如:
1. 变化量:Delta表示两个数之间的差异或者变化量,通常用于表
示变化率或者增量。
例如,Δx表示x的变化量。
2. 极限:Delta通常用于表示变量的极限值,例如,Δx当x趋近于
零时的极限值。
3. 三角形面积:Delta也可以用来表示三角形的面积。
例如,当给
定两条边和它们之间的夹角时,就可以使用三角形面积公式计算出三角形
的面积。
4. 投影:Delta也可以用于表示向量的投影。
例如,当给定向量a
和向量b时,可以使用向量投影公式计算出向量b在向量a的方向上的投影。
5. 泊松分布:Delta常常用于表示泊松分布的参数。
例如,λ表示
泊松分布中每个单位时间内事件的平均发生率,Δλ表示泊松分布的参
数的变化量。
总之,Delta是一个非常常见的数学符号,在数学中有着广泛的应用。

数学中的欧米伽符号通常表示为大写希腊字母Ω(omega)。
它在不同的上下文中可能有不同的意义,以下是几种常见的用法:
1. 角速度:在物理学和工程学中,欧米伽符号通常表示角速度。
角速度是物体绕固定轴旋转的速度,通常用弧度/秒(rad/s)作为单位。
2. 复数单位根:在复数理论中,欧米伽符号Ω表示复数单位根。
一个复数单位根是一个复数,它的某个正整数幂等于1。
特别地,e^(iΩ) = 1,其中i是虚数单位。
3. 渐进符号:在算法复杂度分析中,Ω符号用于表示算法的最低渐进时间复杂度。
它表示给定算法的最好情况下的运行时间下界。
4. 集合论:在集合论中,Ω符号通常用于表示集合的大小或者基数。
例如,|A|表示集合A 的元素数量。
请注意,欧米伽符号在不同的数学领域和文脉中可能具有不同的意义。
因此,在具体的数学问题中,需要根据上下文来理解欧米伽符号的含义。
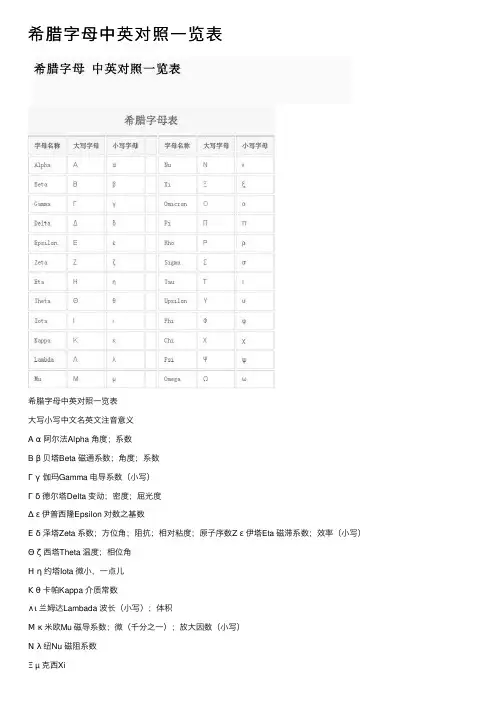
希腊字母中英对照⼀览表希腊字母中英对照⼀览表⼤写⼩写中⽂名英⽂注⾳意义A α阿尔法Alpha ⾓度;系数B β贝塔Beta 磁通系数;⾓度;系数Γγ伽玛Gamma 电导系数(⼩写)Γδ德尔塔Delta 变动;密度;屈光度Δ ε伊普西隆Epsilon 对数之基数Εδ泽塔Zeta 系数;⽅位⾓;阻抗;相对粘度;原⼦序数Ζε伊塔Eta 磁滞系数;效率(⼩写)Θζ西塔Theta 温度;相位⾓Ηη约塔Iota 微⼩,⼀点⼉Κθ卡帕Kappa 介质常数∧ι兰姆达Lambada 波长(⼩写);体积Μκ⽶欧Mu 磁导系数;微(千分之⼀);放⼤因数(⼩写)Νλ纽Nu 磁阻系数Ξ µ 克西XiΟν欧⽶克隆Omicron∏π派Pi 圆周率=圆周÷直径=3.1416Ρξ柔Rho 电阻系数(⼩写)∑ ζ西格玛Sigma 总和(⼤写),表⾯密度;跨导(⼩写)Ση陶Tau 时间常数Τυ⽟普西隆Upsilon 位移Φθ弗爱Phi 磁通;⾓Υχ凯ChiΦψ普赛 Psi ⾓速;介质电通量(静电⼒线)Αα,⾳名?ιθα,希腊语字母名称叫做/?alfa/,美国英语叫做alpha(国际⾳标/'?lf?/),alpha常⽤作形容词,以显⽰某件事物中最重要或最初的。
它是元⾳字母,它表⽰/a/这个⾳,在美国英语⾥⾯变成了元⾳字母a,在俄语字母⾥变成了元⾳字母а。
Ββ,⾳名β?ηα,希腊语字母名称叫做/vita/,美国英语叫做beta(国际⾳标/'bet?/),beta也能表⽰电脑软件的测试版,通常指的是公开测试版,提供⼀般使⽤者协助测试并回报问题。
它是辅⾳字母,在古希腊语,β读作/b/,但现代希腊语读作/v/,现代希腊语以"κπ"代表/b/⾳。
在美国英语⾥,变成了辅⾳字母b,在俄语⾥变成了辅⾳字母б。
希腊字母Γγ,⾳名γ?κκα,希腊语字母名称叫做/??ama/,美国英语叫做gamma(国际⾳标/'g?m?/),它是辅⾳字母,表⽰/?/这个⾳。

delta希腊字母写法全文共四篇示例,供读者参考第一篇示例:Δ德尔塔是希腊字母表中的第四个字母,音标为δ,英语中的音标为/ˈdɛltə/。
它是一个常用的数学符号,在物理、工程学、经济学等领域都有广泛的应用。
Δ的写法和发音在不同语言和地区会有差异,本文将主要介绍它在希腊语中的写法以及一些相关知识。
在希腊字母表中,Δ的写法是一个三角形,上面有一条横线,类似于希腊字母Λ(lambda)的形状。
Δ的发音是/delta/,用于表示一些特定的概念和量。
Δ在数学中常用来表示差量、增量、变化率等概念,例如Δx表示x的增量,Δy表示y的增量,Δt表示t的差量。
在物理学中,Δ也常用来表示变量的变化率,如速度的增量Δv、位移的增量Δr等。
在工程学中,Δ常用来表示系统的变化或改善,如ΔS表示系统的熵变,ΔH表示系统的焓变。
在化学和生物学中,Δ也有类似的用法,用来表示反应的变化或者性质的变化。
除了表示增量和变化率外,Δ还有一些特殊的用法。
在数学中,Δ也经常用来表示差分算子,即Δf(x)表示函数f(x)的差分。
在统计学中,Δ也用来表示变量的离散程度,如ΔX表示随机变量X的离散程度。
在微积分中,Δ也表示极限的逼近程度,如Δx表示x的无穷小增量。
Δ是一个非常重要且广泛应用的数学符号,它在各个领域都有着不同的用途和含义。
Δ的写法虽然简单,但是它所代表的概念和含义却是非常丰富和深刻的,对于理解和研究一些复杂的问题至关重要。
希望通过本文的介绍,读者能对Δ的写法和用法有一个更深入的了解,同时也能对数学和科学有更深入的认识和理解。
第二篇示例:希腊字母是一种古老的文字系统,被广泛应用于数学、物理、化学和工程等领域。
希腊字母中的第四个字母是“Δ”,即delta。
Delta 字母在希腊字母表中的位置是第四个,其形状类似于一个三角形,因此被称为delta。
在数学中,delta通常代表一个变化量或者差异量,广泛应用于微积分和数值分析等领域。
在物理学中,delta也常用于表示热量的变化或者能量的变化等概念。

基本粒子的希腊字母-概述说明以及解释1.引言1.1 概述基本粒子是构成物质世界的最基本单位,它们被认为是构成一切物质和能量的基本要素。
这些粒子有着不同的特性和相互作用,它们的研究对于理解宇宙的组成和性质至关重要。
在物理学中,基本粒子通常用希腊字母来表示和命名。
希腊字母作为国际通用的符号,拥有丰富的含义和符号化的数学表达能力。
因此,在研究和交流基本粒子的领域中,使用希腊字母来表示不同的粒子类型和性质是一种约定俗成的惯例。
这篇文章将系统地介绍基本粒子中使用的希腊字母,包括它们的名称、符号以及与之对应的物理意义。
我们将从最基本的希腊字母开始,逐渐介绍更复杂的符号和粒子。
通过了解和学习这些希腊字母,读者将能够更好地理解和解读物理学文献中涉及的基本粒子性质和相互作用的描述。
此外,对于从事基础研究或教学工作的科学家和教育工作者来说,掌握这些希腊字母也是必要的。
本文的结构按照逻辑顺序进行编排,首先介绍基本粒子中使用的希腊字母,然后按照重要性和相关性进行分类和讨论。
我们将逐一介绍每个字母的音标、大写和小写形式,并给出相应的物理意义。
最后,本文将对已有的研究做出总结,并展望未来研究的发展方向。
通过本文的阅读,读者将能够更全面地了解基本粒子和希腊字母之间的关系,为深入了解物质世界的基本组成和性质奠定基础。
希望本文能够对广大读者的学习和研究有所帮助。
1.2 文章结构文章结构是指文章的整体组织方式,它反映了文章的逻辑关系和内容呈现的次序。
本文的结构共分为三个部分:引言、正文和结论。
在引言部分,我们将以概述、文章结构和目的为主要内容进行叙述。
首先,在概述部分,我们将简要介绍基本粒子的概念和其在物理学中的重要性。
基本粒子是组成物质的最基本单位,研究其性质和相互作用关系对于了解宇宙的本质和探索新物理现象具有重要意义。
接着,在文章结构部分,我们将详细说明本文的组织框架和每个章节的主要内容。
本文将首先介绍基本粒子的希腊字母表示法,包括常见的希腊字母和它们在物理学中的应用。


entomos希腊语含义Entomos是希腊语εντόμος 的变体形式,它的字面意思是“昆虫”。
在希腊语中,entomos一词常被用来描述昆虫类的生物,参考了许多不同的方面和含义。
下面我将为您介绍entomos在希腊语中的一些相关参考内容。
1. 学科名词:在生物学中,entomos指的是昆虫学,也就是研究昆虫的科学。
这个词常常用来描述关于昆虫生物学、分类学、生态学等方面的研究领域。
希腊字母表中的其他学科名词也经常使用类似的形式,例如zoology(动物学),botany(植物学)等。
2. 昆虫的丰富多样性:entomos还可以用来表达关于昆虫世界中的丰富多样性。
希腊是一个地理和生态条件多样的国家,拥有大量种类繁多的昆虫物种。
这个词可以用来形容希腊境内的昆虫种类丰富多样,并且强调了昆虫在生态系统中的重要角色.3. 昆虫文化意象:在希腊传统文化中,昆虫在宗教、神话和艺术中都有重要的象征意义。
例如,蜜蜂在希腊神话中被视为圣洁和勤劳的象征。
蜜蜂在希腊文化中被普遍认为是神圣的昆虫,生产蜂蜜和蜂蜡。
因此,entomos一词也可以与希腊的文化和传统联系起来,并涉及到一些关于昆虫的神话、故事等方面的内容。
4. 昆虫与环境保护:由于昆虫在生态系统中的重要性,保护昆虫对于生物多样性和环境保护至关重要。
希腊的一些环保组织和研究机构也使用entomos一词,来描述他们在保护昆虫及其栖息地方面所做的工作。
这包括监测昆虫种群的数量和状况、研究昆虫对环境变化的响应等。
综上所述,entomos一词在希腊语中有很多相关参考内容。
它可以用来描述昆虫学,昆虫的种类丰富多样性,昆虫在希腊文化中的象征意义,以及昆虫保护等方面的工作。
这个词反映了希腊人对昆虫世界的重视和对生态系统的关注。

表示得分的希腊字母希腊字母在数学、物理、化学等科学领域中被广泛使用,用于表示各种概念、方程、函数等。
其中也有一些希腊字母特指表示得分或评分的含义,特别是在教育领域中常见。
本文将介绍一些在教育领域中用于表示得分的希腊字母,以及它们在各个国家和地区的具体含义和应用。
1. α (Alpha)希腊字母α在表示得分时往往被用来表示最高分或成绩优秀。
在一些国家和地区,特别是欧洲和北美洲的教育系统中,α为最高分,代表学生取得了优秀的成绩。
在这些地区,α常常与其他希腊字母一起使用,构成一个成绩等级体系,用于评估学生的学术表现。
在一些大学和高中的成绩单上,α经常用来表示A或A+,代表学生在该门课程中取得了最高分。
学校通常会按照一定的标准,将学生成绩划分为不同的等级,例如A为优秀,B为良好,C为中等,D为及格,E为不及格等。
2. β (Beta)希腊字母β在表示得分时通常用来表示良好或中等成绩。
与α相比,β的等级一般稍低一些,但仍然代表学生取得了不错的成绩。
在一些国家和地区的教育系统中,学生通常会被评定为α、β、γ等不同的等级。
β的具体含义和应用可能因地区而异。
在某些地区,β等于B或B+,代表良好成绩;而在其他地区,β等于C或C+,代表中等成绩。
每个地区的教育系统都会有自己的评分标准,所以具体的β等级会因不同学校、不同课程而有所差异。
3. γ (Gamma)希腊字母γ在表示得分时往往用来表示及格或一般成绩。
在某些地区的教育系统中,γ等于D或D+,代表学生刚刚及格。
γ等级通常被视为一种警告信号,提示学生在该门课程中的表现需要改善。
在一些国家和地区,学校会将γ等级分为多个子等级,以更精细地评估学生的学术表现。
例如,γ-代表略低于及格,γ+代表略高于及格。
这些细分的等级有助于学生了解自己的学习成果,并提供改进的机会和建议。
4. δ (Delta)希腊字母δ在表示得分时一般用来表示不及格或较差成绩。
δ等级通常代表学生在该门课程中未达到及格标准,需要进行进一步的学习和改进。

希腊字母的哲学含义-概述说明以及解释1.引言1.1 概述概述希腊字母是古希腊文明中的一种特殊的字母系统,它们不仅仅是一种书写工具,更承载着丰富的哲学含义。
这些字母代表了希腊古代哲学家们对世界、人类和宇宙的深刻思考和探索。
通过研究希腊字母的哲学含义,我们可以更好地理解希腊古代哲学的精髓和智慧。
本文将通过分析希腊字母的哲学含义,探讨其在古希腊哲学中的重要性和意义。
首先,我们将介绍文章的结构和目的,以及对希腊字母的整体概述。
接着,我们将详细讨论希腊字母在古希腊哲学中的不同要点,涉及到它们的象征意义和哲学思想。
最后,我们将总结主要观点,并讨论希腊字母的哲学含义对于我们理解古希腊哲学的重要性。
希腊字母的哲学含义不仅仅体现在它们的形象上,更重要的是它们所代表的思想和智慧。
通过对希腊字母的研究,我们可以深入思考古希腊哲学家们对人类和宇宙的认知,以及他们对道德、伦理和知识的思考。
希腊字母的哲学含义是古希腊哲学的核心,也是我们理解古希腊文明的重要窗口。
文章将通过系统地探讨希腊字母的哲学含义,以期能深刻理解古希腊哲学的精髓和智慧。
无论是在西方哲学的发展中,还是在现代社会的学术研究中,希腊字母的哲学含义都扮演着重要的角色。
希望本文能够为读者带来新的思考和启迪,进一步丰富我们对古希腊哲学的认识和理解。
总结而言,本文将对希腊字母的哲学含义进行全面的分析和探讨,通过对其象征意义和哲学思想的解读,深入理解希腊古代哲学的智慧和价值观。
希腊字母不仅仅是一种字母系统,更是古希腊哲学的重要组成部分。
通过研究和理解希腊字母的哲学含义,我们可以更好地把握古希腊哲学的核心思想,并更加深入地思考人类生活和宇宙的意义。
1.2文章结构2. 正文2.1 第一要点在了解希腊字母的哲学含义之前,我们先来了解一下希腊字母的起源和发展历程。
希腊字母是一种古老而有着深厚文化底蕴的文字系统,最早出现在公元前9世纪左右。
希腊字母的演变过程中融入了不少哲学思想,这些思想对于希腊文化的发展起到了积极的推动作用。

希腊字母的cash值-概述说明以及解释1.引言1.1 概述希腊字母是一种古老而重要的字母系统,起源于希腊文明的早期。
这些字母作为希腊人的书写工具和语言表达形式,承载着丰富的历史与文化内涵。
本文将深入探讨希腊字母的起源、发展与演变,以及在不同领域中的应用。
此外,我们还将关注希腊字母在现代社会中的重要性以及其背后的意义,尤其是它们所代表的cash值。
在希腊文明的初期阶段,人们使用的是线性文字B,这是一种类似于楔形文字的书写系统。
然而,在公元前9世纪左右,希腊人逐渐开始采用自己独特的字母系统,也就是我们现在所熟知的希腊字母。
这些字母由不同数量的直线组成,形状独特、简洁而富有艺术感。
希腊字母的使用迅速传播,很快成为了希腊文化中不可或缺的一部分。
希腊字母经历了漫长的历史发展过程,尤其是在古希腊和罗马时期。
在这段时期,希腊字母系统逐渐稳定下来,并融入到了数学、自然科学、哲学、文学等学科领域中。
例如,希腊字母被广泛应用于数学符号,如表示未知数的x、角度的θ、和Σ表示求和等。
同时,希腊字母也在物理学、化学、天文学等领域中扮演重要角色,被用于命名天体、粒子、分子等。
然而,希腊字母的重要性不仅仅局限于学术领域。
它们也在现代社会中扮演着重要的角色。
希腊字母被广泛应用于各种标识符号、品牌标志和社会组织的名称中,为这些实体赋予了独特的身份和形象。
此外,希腊字母还经常被用作演讲、议论和出版物中的修辞手法,以增添文学作品和演讲的艺术感。
在本文中,我们还将探讨希腊字母背后的意义和cash值。
希腊字母所代表的不仅仅是一种语言和符号系统,更是希腊文明和思想的象征。
它们承载着希腊古代智慧、哲学思想和民族精神的传承,代表着人类对知识、智慧和美的追求。
通过深入了解希腊字母的cash值,我们可以更好地理解这些字母的文化价值,以及它们对现代社会的重要性。
总之,本文将全面探讨希腊字母的起源、发展与演变,以及在不同领域中的应用。
通过对希腊字母在现代社会中的重要性和cash值的探索,我们将进一步认识和赞赏这一古老而独特的字母系统在文化和社会中的作用。

数学希腊符号读法大全
我们在学习数学过程中,会接触到许多不同的希腊符号,这些符号代表着不同的数学概念,所以读懂这些希腊符号的读法对我们的数学学习都有很大的帮助。
下面给大家介绍一些常见的数学希腊符号读法:
Alpha:埃尔福特。
Beta:贝塔。
Gamma:伽马。
Delta:德尔塔。
Epsilon:埃普西龙。
Zeta:泽塔。
Eta:伊塔。
Theta:索塔。
Iota:约塔。
Kappa:卡帕。
Lambda:拉姆达。
Mu:缪。
Nu:努。
Xi:克西。
Omicron:奥米克隆。
Pi:派。
Rho:罗。
Sigma:西格玛。
Tau:陶波。
Upsilon:欧普西龙。
Phi:菲。
Chi:克。
Psi:普西。
Omega:欧米伽。
有了这些希腊符号的读法,在我们学习数学时就可以轻松地掌握数学概念,也可以方便地表达不同的数学概念。
因为使用希腊字母可以简化表达,它给我们的数学学习提供了很大的帮助。
所以,要学会希腊符号的读法,记住它们的发音,这对我们的数学研究也具有非常重要的意义。
omega数学符号
数学是一门神秘而又神奇的学科,有时它可以让我们领略到宇宙的美,而有时它也会令我们迷惑不解。
数学符号是数学的重要组成部分,它们是描述数学的基本元素,而其中最重要的一个符号就是omega 数学符号。
omega数学符号是一个希腊字母,在希腊文中它的读音为“ómega”,在不同类型的数学中它有不同的含义。
比如,在概率统计学中,omega 符号表示事件A的概率。
在几何学中,omega符号表示一个多边形的边数。
它也被用来表示无穷的概念,比如实数的无穷大,微积分中的无穷积分等。
在抽象代数中,omega符号表示一个群的长度。
而在离散数学中,它表示一个集合的全排列的个数,又可以作为拓扑学中的性质量组,用来描述底空间的有向边界,也可以用来作为描述几何体表面角的概念。
omega数学符号有许多有用的应用,它可以帮助我们解决许多问题,比如帮助我们计算概率,几何图形的边,集合的全排列等等。
它也可以用来计算无穷大的东西,比如无穷积分,拓扑学里的性质量组等等。
值得一提的是,omega数学符号并不只是纯粹的数学概念,它也可以用在其他不同的学科中,比如物理学,化学学等等,只要有数学涉及的地方,那么omega数学符号就会出现。
总的来说,omega数学符号的知识很重要,它不仅是一种符号,
也是一种知识,能够帮助我们解决许多数学问题,以及在物理化学等学科中也有广泛的应用。
好好学习,掌握omega数学符号,给你带来更多的有趣的知识!。
德尔塔符号公式
德尔塔符号是在数学和物理学中广泛使用的一种特殊符号,通常表示两个实数、向量或矩阵中的一个差异或变化值。
德尔塔符号通常用希腊字母Δ(大写delta)来表示。
在不同的情况下,德尔塔符号具有不同的含义和用法,下面是一些常见的应用示例:
1. 变化量:德尔塔符号可以表示一个量的变化量或差异。
例如,如果 x 和 y 是两个实数,则Δx 可以表示 x 的变化量,即Δx = x2 - x1。
2. 误差:在测量和近似计算中,德尔塔符号常用于表示一个量的误差或不确定性。
例如,如果 x 是一个测量值,Δx 可以表
示该测量值的误差范围。
3. 离散差分:在数值计算中,德尔塔符号可以表示离散差分运算。
例如,对于一个离散函数 f(x) 的差分,可以写为Δf(x) =
f(x+Δx) - f(x)。
4. 变量替换:德尔塔符号也可以用于表示变量的替换或变换。
例如,如果有一个变量 x 和它的替换量Δx,可以用 x' = x +
Δx 来表示替换后的新变量。
需要注意的是,德尔塔符号的具体含义和用法可能在不同的学科和上下文中略有不同。
因此,在具体应用中,应根据上下文和定义来确定德尔塔符号的意义。
随机变量希腊字母读法在统计学中,随机变量希腊字母读法是一种常见的表达方式,用于描述概率变量,使用固定的希腊字母来表示。
在应用中,这是一种重要的表达方式,能够更加精细的描述统计变量。
什么是随机变量希腊字母读法?随机变量希腊字母读法是指在描述随机变量时,使用不同的希腊字母来表示,它是一种快速表达方式,避免了出现多重描述,也可以更加清晰的表达思想。
常用的随机变量希腊字母有α(alpha)、β(beta)、Γ(gamma)、Δ(delta)、ε(epsilon)、η(eta)、μ(mu)、λ(lambda)。
α是指参数,是指在概率分布中,确定概率分布的因素,是概率变量影响的重要因素。
β指的是回归参数,是指统计分析中,从多个变量中求出的参数,用来衡量某些变量对其他变量的影响程度。
Γ是指某个变量的对数均值,是指在某些概率分布中,概率变量的数值期望,一般表示为概率变量的b平均值。
Δ是指分位数,又称指标值,是指在概率分布中,概定概率分布某一部分的比例,是概率分布的重要参数。
ε是指方差,是指在推断统计时,要求的抽样误差,一般表示为概率变量的方差。
η是指偏度,是指在推断统计时,要求的抽样分布的偏度,一般表示为概率变量的均值和方差之间的关系。
μ是指均值,是指在概率分布中,概率变量的数值期望,一般表示为概率变量的平均值。
λ是指卡方分布,是指在概率论中,服从卡方分布的随机变量,从而表达该随机变量的特性。
从上面的内容可以看出,随机变量希腊字母读法是一种重要的表达方式,能够更加精细的描述统计变量。
它的应用能够提高统计分析的准确性,为统计分析提供了新的线索,在统计学中被广泛应用。
此外,在应用随机变量希腊字母读法的过程中,还要根据不同的概率分布,使用不同的希腊字母,以及搭配不同的参数来表达,这就要求我们在使用时要掌握这些希腊字母的描述方式以及概率分布的参数变化规律。
总的来说,随机变量希腊字母读法是在统计分析中一种重要的表达方式,充分利用它能够更加有效地描述统计变量,优化数据分析。
大写字母数学写法大写字母在数学中有着重要的意义,常常代表着一些特定的含义,如矩阵、向量、集合等。
接下来我们将分别介绍几种涉及大写字母的数学写法,以及它们的相关参考内容。
(一)大写希腊字母大写希腊字母在数学中用途广泛,它们代表着不同的数学符号。
以下是常见的大写希腊字母及它们的意义:1. $\Gamma$ 代表着伽玛函数(Gamma Function)。
2. $\Delta$ 代表着三角形的面积,或者是变化量的意义。
3. $\Theta$ 代表着渐近符号。
例如,在算法复杂度分析中,我们通常用 $\Theta$ 符号来表示算法的最坏情况复杂度。
4. $\Lambda$ 代表着二项分布(Binomial Distribution)。
5. $\Xi$ 代表着巨正则系综(Grand Canonical Ensemble)。
6. $\Pi$ 代表着乘积符号(Product Notation)。
7. $\Sigma$ 代表着求和符号(Summation Notation)。
8. $\Phi$ 代表着高斯函数(Gaussian Function)。
9. $\Psi$ 代表着波函数(Wave Function)。
以上是一些常见的大写希腊字母及它们的意义,当然还有很多其他的希腊字母,在数学中有着重要的意义。
(二)大写罗马字母在数学中,大写罗马字母的使用也非常普遍。
以下是几个常见的大写罗马字母及其意义:1. $A$ 代表着矩阵(Matrix)。
2. $B$ 代表着向量(Vector)。
3. $C$ 代表着复数(Complex)。
4. $D$ 代表着微分(Differential)。
5. $E$ 代表着自然常数(e)。
6. $F$ 代表着强度(Force)。
7. $G$ 代表着万有引力常数(Gravity)。
8. $H$ 代表着哈密顿量(Hamiltonian)。
9. $I$ 代表着单位矩阵(Identity Matrix)。
字母符号字母符号是指由字母组成的特殊符号。
它们通常用于不同的场合,例如数学公式、特殊符号的表示和简写等。
字母符号不仅可以提供更丰富的表达方式,还可以简化信息的传递和记录。
本文将介绍一些常见的字母符号及其用法。
1. 希腊字母希腊字母是希腊语中使用的字母,它们常用于数学、科学和工程领域。
以下是一些常见的希腊字母及其对应的表示方式:•α(alpha):表示角度、系数、透射率等;•β(beta):表示角度、系数、速度等;•γ(gamma):表示角度、系数、导热系数等;•δ(delta):表示差值、变化量、面积等;•ε(epsilon):表示介电常数、极小量等;•θ(theta):表示角度、温度等;•λ(lambda):表示波长、衰减系数等;•μ(mu):表示动态摩擦系数、线性质量等;•ω(omega):表示角速度、圆频率等。
希腊字母不仅可以表示数学和物理概念,还可以用于表示各种变量和常数。
在Markdown中,可以使用$\\alpha$、$\\beta$等符号来表示希腊字母。
2. 拉丁字母的变形拉丁字母是指源自拉丁语的字母,它们被广泛应用于各个国家的语言文字系统中。
有些拉丁字母的大小写形式与希腊字母相似,但具有不同的含义和用法。
以下是一些常见的拉丁字母变形及其用法:•∂(partial):表示偏导数;•∆(delta):表示变化量、差分;•∑(sigma):表示求和;•∫(integral):表示积分;•√(root):表示平方根;•≠(not equal):表示不等于;•≤(less than or equal to):表示小于等于;•≥(greater than or equal to):表示大于等于。
这些拉丁字母的变形符号在Markdown中可以通过使用$\\partial$、$\\Sigma$、$\\int$等代码来表示。
3. 其他符号除了希腊字母和拉丁字母的变形,还有一些其他字母符号常用于数学和科学领域。
希腊字母的不同意思
希腊字母是希腊语所使用的字母,常被用于科学、数学、工程等领域。
然而,同一个希腊字母在不同的上下文中,往往有不同的含义。
比如:
1. α (alpha):在数学中表示角度;在化学中表示“首位”或“α粒子”;在物理学中表示角加速度;在金融学中表示股票的超额收益率。
2. β (beta):在数学中表示变量;在化学中表示“β-粒子”或“双键”;在物理学中表示电子的速度;在金融学中表示股票的风险。
3. γ (gamma):在数学中表示伽玛函数;在化学中表示“γ射线”;在物理学中表示角加速度;在金融学中表示股票的敏感性。
4. δ (delta):在数学中表示变化量或增量;在化学中表示“δ键”或“δ-酸”;在物理学中表示电子的电荷量;在金融学中表示股票的期权价格变化。
除此之外,希腊字母还有许多其他的含义,需要根据具体上下文来理解。
因此,学习希腊字母不仅要掌握它们的形状和发音,还要了解它们在不同领域中的应用和含义。
- 1 -。