当前位置：文档之家 › 4刚体转动及角动量守恒

4刚体转动及角动量守恒

  • 格式：ppt
  • 大小：2.87 MB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律

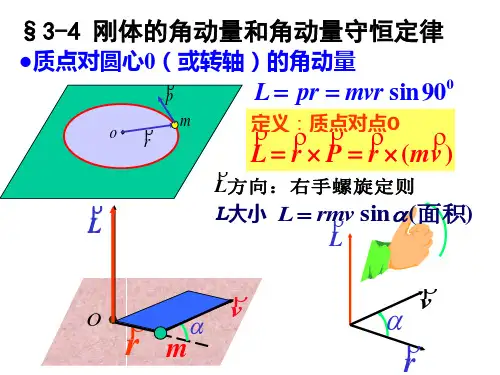
刚体定轴转动的角动量定理和角动量守恒定律
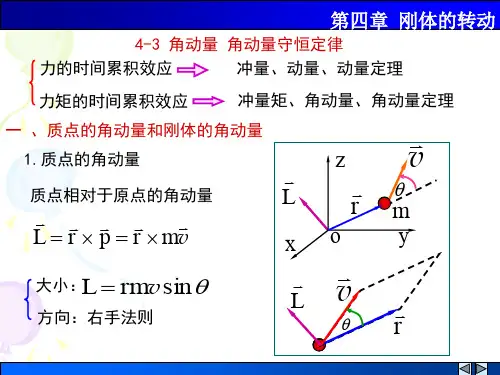
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积；方向与角速度的方向相同。

2、刚体定轴转动的角动量定理
（1）微分形式：刚体绕某定轴转动时，作用于刚体的合外力矩，等于刚体绕该定轴的角动量随时间的变化率。

（2）积分形式：当物体绕某定轴转动时，作用在物体上的冲量矩等于角动量的增量。

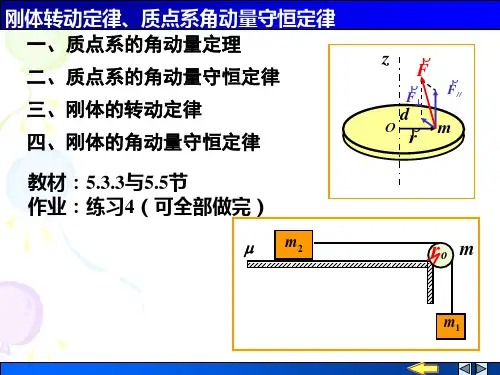
3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零，或者不受外力矩作用，物体的角动量保持不变。

练习：1角动量守恒的条件是 。

0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ） 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。

刚体动力学刚体的转动与角动量守恒定律

刚体动力学刚体的转动与角动量守恒定律

刚体动力学刚体的转动与角动量守恒定律刚体动力学——刚体的转动与角动量守恒定律刚体动力学是研究刚体运动的物理学分支，主要研究刚体的平动和转动。

在刚体的运动过程中，角动量的守恒定律是关键的一条定律，它在很多物理问题的求解中起着重要的作用。

一、刚体转动的基本概念刚体是指具有一定形状和大小的物体，在运动过程中保持其形状和大小不变的情况下，绕一个固定轴线进行旋转。

在刚体转动的过程中，存在着固定轴线上的角位移、角速度、角加速度等概念。

角位移表示刚体在转动过程中的角度变化，通常用符号θ表示；角速度表示单位时间内刚体转动的角度变化率，通常用符号ω表示；角加速度表示单位时间内角速度的变化率，通常用符号α表示。

二、刚体的转动与力矩刚体在转动过程中需受到外力的作用，这些外力可以将刚体带动产生转动现象。

力矩是刚体转动的重要力学量，它描述了力对于刚体转动的影响程度。

力矩的大小等于力乘以作用点到转轴的距离，用数学式表示为：τ = F × r其中τ表示力矩，F表示力的大小，r表示作用点到转轴的距离。

三、刚体的转动惯量与角动量刚体的转动惯量与角动量是刚体转动过程中的另外两个重要概念。

转动惯量描述了刚体对于转动的惯性程度，它的大小取决于刚体的质量分布和几何形状。

角动量描述了刚体在转动过程中的旋转性质，它等于刚体质量的转动惯量乘以角速度，用数学式表示为：L = I × ω其中L表示角动量，I表示转动惯量，ω表示角速度。

四、角动量守恒定律角动量守恒定律是刚体动力学中的一个基本定律，它表明在没有外力矩作用的情况下，刚体转动过程中的角动量保持不变。

如果一个刚体在初态时角动量为L1，在末态时角动量为L2，且没有外力矩作用，则有L1 = L2。

这一定律体现了一个自然规律，对于理解刚体的转动过程和求解相关物理问题具有重要意义。

五、应用案例角动量守恒定律可以应用于各种实际物理问题的求解中，例如刚体的转动稳定性、陀螺的运动等。

第三章 4刚体角动量和守恒

第三章 4刚体角动量和守恒

核融合能量的分界—铁
自转初每秒钟 30 - 40次 4 秒自转一次老化的 磁场地球的108～1015倍 产生脉冲波(波霎)周期 0.03～4.3秒 一亿吨/cm3 表面光滑
▲行星状星云，中间的白点可能是中子星
【例15】 一匀质细棒长为l ，质量为m，可绕通过其端点 O的水平轴转动，图示。当棒从水平位置自由释放后，它
【例13】 质量为 m1长为 l 的细杆，静止平放在粗糙的水平面上， 细杆与水平面之间的摩檫系数为 μ ，可绕通过其端点O，且与
平面垂直的固定轴转动。 另有一水平运动的质量为 m2 的滑快， 从侧面垂直与杆的方向，与杆的另一端A 碰撞。已知滑块碰撞
o 前、后的速度分别为
檫力矩。 ：（2）
v1 与 v 2 求：（1）细杆转动时受到的摩 杆从开始转动到停止所需的时间.
●地球的自转角速度变化？ 变慢！
问题2 水平圆盘边上，站有一人质量为m，圆盘半径为R， 转动惯量为J，以角速度ω转动，如果此人从旁边径直走 到圆盘中心，求：角速度的变化和系统动能的变化？
O
A知识点窍:相对运动和L守恒(系统受的合外力矩为零),
L Li 常量C ,转动动能 E转 J 2 2
B逻辑推理:速度对惯性参照系,行走过程中摩擦力过转轴 （Mf=0）,重力矩与L垂直就是对L没有贡献，即M合=0
C解：（1）求摩擦力矩 取微元dx
dm=dx= m1 dx
x
m1 l
l
dx
对o点的力矩元 dM0 dM0 = x dmg
dM0
=
m1 l
g
x
dx
x
M0 =
l m1g x dx
0l
1 2
m1gl
【例13】 质量为 m1长为 l 的细杆，静止平放在粗糙的水平面 上，细杆与水平面之间的摩檫系数为 μ ，可绕通过其端点O，
物理-定轴转动刚体的角动量定理和角动量守恒定律

物理-定轴转动刚体的角动量定理和角动量守恒定律


或 Lz = I = 恒量
当刚体相对惯性系中某给定转轴的合外力矩为 零时，该刚体对同一转轴的角动量保持不变。
——对转轴的角动量守恒定律
二、定轴转动中的角动量守恒
说明 1、 关于该守恒定律的条件：
Mz Miz 0
特别地，若每一个力的力矩均为零，即 则
二、定轴转动中的角动量守恒
M iz ri Fi sini 0 的几种情况
10
f
20
O1 R1 A
R2 O2 fB
随堂练习
当两圆柱接触处无相对滑动时，两者转速相反
10
20
O1 R1 A
R2 O2 B
且两者接触点的线速率相等！
二、定轴转动中的角动量守恒
由定轴转动的角动量定理
Mz
dLz dt
若刚体所受对转轴的合外力矩 M z 0，则有
dLz d ( I ) 0
dt
dt
二、定轴转动中的角动量守恒
(3) 对共轴非刚体系（其中各质元到转轴的距离可 变则）系：统的转动惯量可变，此时系统对转轴的角动量守恒，
即：I =恒量
• 特别地，若各质元的 保持一致，
Lz =I =恒量
当 I 增大时， 就减小； 当 I 减小时， 就增大 。
二、定轴转动中的角动量守恒
例如：花样滑冰运动员在冰面上旋转时 运动了角动量守恒定律
（1）
（2）
（3）
二、定轴转动中的角动量守恒
2、对转轴的角动量守恒定律的适用范围： • 不仅适用于刚体， • 也适用于绕同一转轴转动的任意质点系。
二、定轴转动中的角动量守恒
3、对转轴的角动量守恒的几种典型表现 (1) 对定轴刚体：I 不变， 大小和方向均不变；
刚体转动及角动量守恒ppt

刚体转动及角动量守恒ppt


匀直细杆对端垂轴旳
平行移轴定理
对质心轴旳转动惯量 对新轴旳转动惯量
质心
例如：
时
新轴对心轴旳平移量
新轴 质心轴
代入可得 端
匀质薄圆盘对圆心垂盘轴算旳 例
取半径为 微宽为 旳窄环带旳质量为质元
球体算例 匀质实心球对心轴旳 可看成是许多半径不同旳共轴 薄圆盘旳转动惯量 旳迭加 距 为 、半径为 、微厚为 旳薄圆盘旳转动惯量为
a = Rb
T2 – m2 g = m2a ( T1 – T2 ) R = Ib
及
I
=
1 2
mR2
得
b=
(m1-m2)g
R(m1+ m2+ m
2)
常量
故
由
m2
a
G2
m1
a
G1
(m1-m2)g
R(m1+ m2+ m 2)
t (m1-m2)g
g 2 (rad)
R(m1+ m2+ m 2)
两匀直细杆
q
转动定两律者瞬例时题角加五速度之比
与 时刻相应，何时
则何时
，
何时 恒定 则何时 恒定。
匀直 细杆一 端为轴 水平静 止释放
转动定律例转题动 二( T2 – T1 ) R = Ib
I=mR2 2
R
m
T2
T1
a
m2
m1
b
平动 m2 g – T2 = m2a
T2
T1
T1 – m1 g = m1a
线-角 a = Rb
T2
T1
联立解得
a
G2
力矩旳功算例 拨动圆盘转一周，摩擦阻力矩旳功旳大小
《大学物理》3.4刚体定轴转动的角动量定理 角动量守恒定律

《大学物理》3.4刚体定轴转动的角动量定理 角动量守恒定律


我国第一颗人造地球卫星沿椭圆轨道绕地球运动， 例：我国第一颗人造地球卫星沿椭圆轨道绕地球运动，地心为该椭圆 的一个焦点。 的一个焦点。已知地球半径 R ，卫星的近地点到地面距离 l ，卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ，求它在远地点速率 v2 。
1 2
卫星在运动过程中，所受力主要是万有引力， 解：卫星在运动过程中，所受力主要是万有引力，其它力忽 略不计，故卫星在运动过程中对地心角动量守恒。 略不计，故卫星在运动过程中对地心角动量守恒。 m
0
r
A
θ = 90
0
mv
质点作圆周运动的角动量
θ
L = rmv = mr ω
2
2.2刚体的角动量 刚体的角动量 刚体对 oz轴的角动量为
z
ω
v
2
i
L = ∑ m r ω = (∑ m r )ω
2 i i i i
o
r
i
m
i
∑ m r 刚体绕 oz 轴的转动惯量
2 i i
L = Jω
L = Jω
刚体对转轴的角动量等于其转动惯量与角速度乘积。 刚体对转轴的角动量等于其转动惯量与角速度乘积。
1 m v 0 a = ( ML2 + ma 2 )ω 3
子弹射入后一起摆动的过程只有重力做功，故系统机 械能守恒。
1 1 L 2 2 2 ( ML + ma )ω = mga (1 cos60°) + Mg (1 cos60°) 2 3 2
ω=
3(2ma + ML)g 2(3ma 2 + ML2 )
二、角动量定理和角动量守恒定理
1× mv 对时间求导 = r × (mv ) + × mv dt dt dt dr d dL ∵ = v , F = (mv ) M = dt dt dt dL 质点所受合外力矩等于质 ∴ = r × F + v × mv dt 点角动量对时间的变化率
(4-2)刚体转动定律、刚体角动量守恒定律

(4-2)刚体转动定律、刚体角动量守恒定律


内
外 外 外 质点系的
内
得
内 质点系所受的
内
外 外
冲量矩 质点系的角动量
矩的矢量和 的时间变化率 若各质点的速度或所受外力与参考点共面，则其角动量或力矩只含正 内力矩在求矢 反两种方向，可设顺时针为正向，用代数和代替矢量和。 量和时成对相消 微分形式 称为
外
角动量增量 质点受外力
刚体转动定律、质点系角动量守恒定律
即：
i j k Mo r F x y z Fx F y Fz i yFz zFy j zFx xFz k xFy yFx




M z xFy yFx
Mz为力对 o 点 的力矩在 z 轴方向的分量
注意. 力矩求和只能对同一参考点（或轴）进行。
另一类常见现象
刚体转动定律、质点系角动量守恒定律 ② J 可变，ω亦可变，但 Jω 乘积不变 茹可夫斯基櫈
张臂
大
用外力矩 启动转盘后 撤除外力矩
收臂 小 大
小
花样滑冰常见例
刚体转动定律、质点系角动量守恒定律 忽略脚底摩擦力矩的作用，角动量守恒 J1 J11 J 22 所以 2 1 J2
在冲击等问题中
M 内力 M外力 L 常量
角动量守恒定律是自然界的一个基本定律，有很多实例
刚体转动定律、质点系角动量守恒定律
角动量守恒现象举例 适用于一切转动问题，大至天体，小至粒子...
茹科夫斯基凳实验 为什么银河系呈旋臂盘形结构？ 为什么直升飞机的尾翼要安装螺旋桨？ 为什么猫从高处落下时总能四脚着地？
1 T1 r T2 r J mr 2 2
T1
r
(3)
4、刚体的能量、角动量守恒

4、刚体的能量、角动量守恒

考虑一个过程，设在力矩作用下，刚体的角位置由 q1q2，角速度由 12，则：
A Md q J dq
θ1
θ2
q2
q2
q1
q1
d J dq dt

2
1
1 1 2 2 J d J 2 J 1 2 2
同力做功的规律相比，可知： 刚体定轴转动的动能定理：合外力矩对转动 刚体所做的功，等于刚体转动动能的增量。
例：质量为m，长为L的细杆一端支以枢轴自由旋转， 设自水平静止释放。求杆过铅直位置时的角速度。
解：杆从水平转到铅直方向的 过程中，只有重力矩做功。
q
mg
A
p /2
0
mgL L mg cos q dq 2 2

由动能定理得：
L 1 1 2 2 mg J J 0 2 2 2
§5-4 刚体定轴转动的功能关系
一、刚体的平动动能和重力势能 其平动动能为各质元动能和：
1 2 E k 平 mi v i i 1 2 1 2 MvC 2 vC为质心的速度 其中：
其重力势能为各 质元势能之和： Z
n
Y
C
M vC
mi
yC
yi
X
O
m y E p mi gy i M M
dr j rM
F
A dA Md q
q0
q
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，做的功就越大。
合力矩的功等于各力矩功的和：
A Md q M i dq M i dq Ai
i
i
i 1
n
dA d q 力矩的功率： P M M dt dt
《大学物理》34刚体定轴转动的角动量定理角动量守恒定律.

《大学物理》34刚体定轴转动的角动量定理角动量守恒定律.

矩为零故角动量守恒。
设子弹射入后杆起摆的角速度为ω，则有：
1 m v 0 a ( ML2 ma 2 ) 3
子弹射入后一起摆动的过程只有重力做功，故系统机 械能守恒。
1 1 L 2 2 2 ( ML ma ) mga (1 cos60 ) Mg (1 cos60 ) 2 3 2
1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
d M J J dt
利用角动量表示
dJ dL M dt dt
刚体绕定轴转动时，作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
当合外力矩为零时
d J dL M dt dt
如果质点所受合外力矩为零，则质点的角动量保持不变， 这就是质点的角动量守恒定律。
1. 质点角动量定理及守恒定律
例：我国第一颗人造地球卫星沿椭圆轨道绕地球运动，地心为该椭圆 的一个焦点。已知地球半径 R ，卫星的近地点到地面距离 l ，卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ，求它在远地点速率 v2 。
3.4刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量 1.冲量矩
定义：力矩与力矩作用时间的乘积称为冲量矩。
数学表达：
M dt
0
t
2.角动量
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
o
r
v
o
L
m

L
r
m
J 恒量
如果物体所受合外力矩为零，或不受外力矩的作用， 物体的角动量保持不变，这就是角动量守恒定律。
大学物理学教程马文蔚43角动量-角动量守恒定律1

大学物理学教程马文蔚43角动量-角动量守恒定律1


解：（1）对子弹、圆盘系统用角动量守恒定律
m00 R
(1 mR2
m020

m0
R2
)
(
1 2
m

m0
)
R
（2）先求摩擦力矩，在圆盘
上取一同轴圆环，如图，则
mOr R
dr 0
m0
dm ds 2 rdr,
m
R2
摩擦力矩
dM
dmgr
第四章 刚体的转动
M
解：小虫与细杆的碰撞视为完全非弹性碰撞，碰撞前后系统角动 量守恒
mv0
l 4

1 12
ml
2

m(
l 4
)2

12 v0
7l
小虫与细杆系统的外力矩为
M mgr cos
第四章 刚体的转动
角速度恒定，由角动量定理
M dL d(J) dJ J 1 ml 2 mr 2
时0各反自向对滑绳行中,交点错的时角动,各量抓为住L长,为他d们的将绳绳索收一拢端为,然d 后时相,各对自旋的转速,率此
为 20 .
2
L

m0
d 2
2m0
d 2

2m
d/2 2
20
d
例8: 两只同重量的猴子,一只用力往上爬,另一只不爬,若滑轮重 量忽略不计,问哪一只先到达滑轮顶端?
R
R
若 M 0 ，则 L J 恒量
讨论：(1) 守恒条件 M 0
若 J 不变，不变；若J 变， 也变，但 L J 不变.
(2) 内力矩不改变系统的角动量.
第四章 刚体的转动
(3)在冲击等问题中,M in M ex L C
刚体定轴转动角动量守恒定律解析

刚体定轴转动角动量守恒定律解析

MR2
2
d
dt
R0
t
t
d dt
0
0
01
ut
(
2m
)
1 2
arctan[ M ]
0
2mu2t 2
MR2
dt
第四u章( 2Mm
1
刚) 2体力学
R
8 22
大学 物理
4-4 刚体定轴转动的角动量守恒定律
角动量守恒定律在工程技术上的应用
陀螺仪与导航
陀螺仪：能够绕其对称轴高速 旋转的厚重的对称刚体。
l 2
处)
解得
t
2 m2
v1 v2
m1g
O
关于摩擦力矩 在x处取dm，dm m1 dx
x l
l
dm
元摩擦力 df dmg
m1
元摩擦力矩 dMr df x dmg x
总摩擦力矩
M r
dMr
l m1 gxdx m1g l 2
0
l
l2
m1g
l 2
第四章 刚体力学
4
大学 物理
4-4 刚体定轴转动的角动量守恒定律
例 一长为l，质量为m0的杆可绕支点O自由转动。一质量为
m，速度为v的子弹射入距支点为a的棒内。若棒偏转角为
30°。问子弹的初速度为多少。
解： 射入过程角动量守恒：
o
mva
1 3
m0l
2
ma2
30°
la
转动过程机械能守恒：
v
1 1 23
m0l 2
ma2
2
mga1 cos30
m0 g
l 2
1 cos30
v 1 ma
g 2 6

刚体的转动 角动量守恒定律


L
r
mv
二.力矩
M
r
F
大小：M
方向： r
rF F
sin
单位： N m 量纲： ML2T 2
三.角动量定理
质点所受的合外力矩等于它的角动量对时
间的变化率
M
dL
dt
2.8 角动量 角动量守恒定律
一L.角动r量 mv二.力M矩 r三.角F动量定理
M
dL
dt
四.角动量守恒定律：如果对于某一固定点，质 点所受的合外力矩为零，则此质点对该固定
x dx
IB
1 3
m L2
1 mL2 12
m
L 2
2
B A h O质
IC
1 XmL2 12
IA
1 12
m L2
m h2
IB
1 mL2 12
m
L
2
2
平行轴定理：绕任意轴的转 动惯量等于绕过质心的平行 的转动惯量加上质量与两轴 间距的平方
I IC md2
d
A
C
例2）半径为R的质量均匀分布的细圆环及薄圆 盘，质量均为m，试分别求出对通过质心并与 环面或盘面垂直的转轴的转动惯量。
质心运动定理反映了物体的平动规律。
2.刚体的定轴转动 刚体的各质元在运动中都绕一固定轴作圆 周运动，称为刚体作定轴转动。
3.刚体的一般运动
蔡斯勒斯定理：刚体的任一位移总可以表示 为一个随质心的平动加上绕质心的转动。
三. 刚体定轴转动的特点
每一质点都作圆心在轴上，圆平面垂直轴，
且角位置.角速度.角加速度都相同的圆周运动
复习
冲量：
dI Fdt
I
动量定理：

刚体定轴转动的角动量定理 角动量守恒定律.


l 1 l 2 2 mv0 m l m( ) 4 12 4
12 v 0 7 l
12 v 0 7 l
由角动量定理
dL d ( I ) dI M dt dt dt
即
d 1 dr 2 2 mgr cos ( ml mr ) 2mr dt 12 dt
※ 刚体定轴转动的角动量定理和角动量守恒定律
刚体定轴转动对轴上一点的角动量（自学） ：
结 论：
一般情况下，刚体定轴转动对轴上一点的角动 量并不一定沿角速度（即转轴）的方向，而是与其 成一定夹角；但对于质量分布与几何形状有共同对 称轴的刚体，当绕该对称轴转动时，刚体对轴上任 一点的角动量与角速度的方向相同.
4 m 2m M
[讨论] ① M>>m ② M<<m
作 业：
7.4.3. 思 考： 7.4.1.
例:
已知均匀直杆(l ,M),一端挂在光滑水平轴上，开始时静止 在竖直位置，有一子弹（m.vo)水平射入而不复出。求杆与子弹 一起运动时的角速度.
解：
子弹进入到一起运动，瞬间完成.
I
i i
i
const.
但角动量可在内部传递。
3 刚体定轴转动的角动量守恒定律 若 M 0 ，则 讨论
守 恒条件:
L I 常量
M 0
若 I 不变， 不变；若 I 变， 也变，但 L I 不变. 内力矩不改变系统的角动量. 在冲击等问题中


M in M ex L 常量
现在讨论力矩对时间的积累效应。
※ 现在讨论力矩对时间的积累效应。 质点系： dL 对点： M 外
dt

3-4 刚体定轴转动的角动量定理和角动量守恒定律


若 M 0 ，则 L r mv 常数
质点所受外力对某固定点的力矩为零，则质点 对该固定点的角动量守恒。这就是质点的角动 量守恒定律。
第3章 刚体力学基础
3–4 刚体定轴转动的角动量定理和角动量守恒定律
4
例3.7 在光滑的水平桌面上，放有质量为M的木块， 木块与一弹簧相连，弹簧的另一端固定在O点，弹簧 的劲度系数为k，设有一质量为m的子弹以初速 v0 垂 直于OA射向M并嵌在木块内.弹簧原长 l0 ，子弹击中 木块后，木块M运动到B点时刻，弹簧长度变为l，此 时OB垂直于OA，求在B点时，木块的运动速度 v2 . 解 击中瞬间，在水平 面内，子弹与木块组成 的系统沿 v0 方向动量守 恒，即有
M t d L L L J J M d t d L L L J J M dd t d L L M L d t J d L J L 0 0 0 0 0 0 L0 0 J J 0 t L L
3–4 刚体定轴转动的角动量定理和角动量守恒定律
24
例3.9 在工程上，两飞轮常用摩擦啮合器使它们以 相同的转速一起转动．如图所示，A和B两飞轮的 轴杆在同一中心线上．A轮的转动惯量为JA＝10 kg· m2，B轮的转动惯量为JB＝20 kg· m2，开始时A 轮每分钟的转速为600转，B轮静止．C为摩擦啮合 器．求两轮啮合后的转速，在啮合过程中，两轮的 机械能有何变化？
第3章 刚体力学基础
3–4 刚体定轴转动的角动量定理和角动量守恒定律
解 以飞轮A，B，啮合器C为系统，系统受到轴向 的正压力和啮合器之间的切向摩擦力。前者对轴的力 矩为零，后者对轴有力矩，但为系统的内力矩，即系 统所受合外力矩为零，所以系统的角动量守恒，即

大学物理——角动量定理和角动量守恒定律


解：把飞船和排出的 废气看作一个系统， 废气质量为m。可以 认为废气质量远小于 飞船的质量，
dm/2
u
Lg
r

L0
u dm/2
上页 下页 返回 退出
所以原来系统对于飞船中心轴的角动量近似地等 于飞船自身的角动量，即
L0＝J
在喷气过程中，以dm表示dt时间内喷出的气体
， 这 些 气 体 对 中 心 轴 的 角 动 量 为 dm·r(u+v) ， 方 向
量为JB=20kgm2 。开始时A轮的转速为600r/min，B
轮静止。C为摩擦啮合器。求两轮啮合后的转速；在 啮合过程中，两轮的机械能有何变化？
A
B
C
A
B
C
A

上页 下页 返回 退出
解：以飞轮A、B和啮合器C作为一系统来考虑，在
啮合过程中，系统受到轴向的正压力和啮合器间的 切向摩擦力，前者对转轴的力矩为零，后者对转轴 有力矩，但为系统的内力矩。系统没有受到其他外 力矩，所以系统的角动量守恒。按角动量守恒定律 可得
由匀减速直线运动的公式得
0 v2 2as
亦即 v 2 2gs
（3）
（4）
由式（1）、（2）与（4）联合求解，即得

3gl 3 2gs
l
（5）
上页 下页 返回 退出
当’取正值，则棒向左摆，其条件为
3gl 3 2gs 0
亦即l >6s；当’取负值，则棒向右摆，其条件
上页 下页 返回 退出
数为 。相撞后物体沿地面滑行一距离s而停止。
求相撞后棒的质心C 离地面的最大高度h，并说明
棒在碰撞后将向左摆或向右摆的条件。
解：这个问题可分为三个阶段

[理学]05-4刚体的角动量定理和角动量守恒定律


双旋翼直升机不需要尾桨，它通过一对转向相反的螺 旋桨，保持系统的总角动量仍然为零
并轴双旋翼直升机通过在同轴心的内外两轴上安装 一对对转的螺旋桨来防止机身反向打转
鱼雷在其尾部也装有对转螺旋桨，其目的也是 为了消除单螺旋桨造成鱼雷自身的反转问题
为什么同手同脚地走路或 跑步会使人觉得别扭呢？ 当一侧的腿向前跨出时，另 一侧的臂必须同时向前摆出， 这样躯干的上端（肩）和下 端（髋）彼此向相反方向扭 转，而躯干的中段和头部则 大体保持在原来位置上，才 可以保证整个身体对于竖直 轴的角动量保持为零 腿臂的动作正确、协调配合，对加大步长、提高步频 都有一定作用，因而对提高跑步速度有明显影响
对绕定轴转动的可变形物体而言，在不同状态下
物体对转轴的转动惯量可能不同，但是如果它所 受合外力矩为零，那么它的角动量也将保持不变
花样滑冰运动员利用四肢的伸缩改变自身的 转动惯量，可以改变绕自身竖直轴的角速度
合外力矩为零不仅是绕定轴转动刚体角动量守恒的
条件，也是任何质点系对角动量守恒的条件

l
M
m
v0
系统的角动量守恒
mv0l J
1 2 2 J ? Ml ml 3

l
M
棒的转 子弹的转 动惯量 动惯量
m
v0
mv0 M ( m)l 3
例1 一质量为M，长为l 的均质细棒，可绕过其顶端的 水平轴自由转动。当杆静止时，一质量为m的子弹以 水平速度v0射入细杆底端并穿出，穿出后子弹速度损 失3/4，求子弹穿出后棒的角速度 O 取子弹和细杆作为系统，在子弹射入 棒端并从棒中穿出的过程中，子弹与 M 细杆之间的作用力为内力，转轴上的 l 作用力和重力不产生力矩，系统所受 m 外力矩为零，系统角动量守恒
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4. 角加速度
匀角速 常量 匀角加速 变角加速
单位：
转动方程求导例题
rad rad s -1
rad s -2 rad
rad s -1 rad s -2
匀变角速定轴转动
rad
150p 100p 50p p 53p 52p 51p 50p
rad s
1
rad s
2
p
t
s
t
s
t
s
积分求转动方程
恒量
且t=0 时
的薄圆盘的转动惯量为
其中
常用结果 匀质薄圆盘
转轴通过中心垂直盘面
匀质细直棒
转轴通过端点与棒垂直
R
m
m
L
1 2 mR I= 2
1 2 m L I= 3
匀质矩形薄板
转轴通过中 心垂直板面
其它典型
匀质厚圆筒
转轴沿几何轴
m I= (a 2 + b 2 ) 12 匀质细圆环
转轴通过中 心垂直环面
m I = 2 (R12 + R22 ) 匀质圆柱体
与
时刻对应，何时 何时
则何时 恒定 则何时
， 恒定。
匀直 细杆一 端为轴 水平静 止释放
转动定律例题二 转动 ( T2 – T1 ) R = Ib
m
R
T2
T1
a
m2 m1
轮轴无摩擦 轻绳不伸长 轮绳不打滑 （以后各例同）
I=mR2 2 b 平动 m2 g – T2 = m2a T1 – m1 g = m1a T1 T2 a = Rb 线-角 T1 T2 联立解得 a a m2 m1 g g a= 1 G1 m1+ m2+ 2 m G2 T1 = m1 ( g + a ) m1 g T2 = m2 ( g – a ) m2 g
=
r
r
转动惯量的计算
将刚体转动定律 M
=I b
与质点运动定律 F
= m a 对比
转动惯量
I
是刚体转动惯性的量度
与刚体的质量、形状、大小 及质量对转轴的分布情况有关
I
∑
质量连续分布的刚体用积分求 I
I I
的单位为
为体积元
处的密度
分立质点的算例
可视为分立质点结构的刚体
转轴
若连接两小球（视为质点） 的轻细硬杆的质量可以忽略， 则
∑
转轴
∑
0.75
质量连续分布的刚体 直棒算例
匀直细杆对中垂轴的 匀直细杆对端垂轴的
平行移轴定理
对质心轴的转动惯量 对新轴的转动惯量 新轴对心轴的平移量 质心 例如： 代入可得 端
时
新轴
质心轴
匀质薄圆盘对心垂轴的 圆盘算例
取半径为 微宽为 的窄环带的质量为质元
可看成是许多半径不同的共轴 匀质实心球对心轴的 球体算例 薄圆盘的转动惯量 的迭加 距 为 、半径为 、微厚为
M = F1 d 1
r Ft 2 r2 F2 d 2 = Ft 叉乘右螺旋 1 r1
转动定律
瞬时 角加速度 瞬时 角速度
某质元
Fi
t
qi
n
fi
∑ Fi ri sin j i + ∑ f i ri sin q i = ∑
合外力矩 M 内力矩成对抵消= 0
得
O
ji
ri
Fi sin j i + f i sin q i = ri b a it =
刚体上 复杂 各质点都 的运动 以某一定 与平动 点为球心 的混合。 的各个球 面上运动。
定轴转动参量
1. 角位置
刚体定轴转动 的运动方程
刚体
刚体中任 一点 (t+△t) (t) 参考 方向
2. 角位移
3. 角速度
静止 常量 变角速
转动平面（包含p并与转轴垂直）
匀角速
转轴 用矢量表 示 或 时，它们 与 刚体的 转动方向 采用右螺 旋定则
转轴通过中心 垂直于几何轴
I=mR2 匀质细圆环
转轴沿着 环的直径
I=
m 2 m 2 L R + 4 12 匀质薄球壳
转轴通过球心
I=
mR 2
2
2 m R2 I= 3
转动定律例题一
合外力矩 应由各分力矩进行合成 。 在定轴转动中，可先设一个正轴向（或绕向），若分力 矩与此向相同则为正，反之为复。 合外力矩 与合角加速度 方向一致。
其法向 n 分量均通过转轴， 不产生转动力矩。 其切向 t 投影式为
Fi 受内力 fi ai Fi + f i =
受外力
等式两边乘以 i 并对所有质元及其所受力矩求和
r
ri
b
b
M
=
∑
ri
转动惯量
瞬时 角加速度 瞬时 角速度
某质元 M
Fi
t
qi
n
fi
刚体所获得的角加速度 ∑ Fi ri sin j i + ∑ f i ri sin的大小与刚体受到的 qi = ∑ ri b 合外力矩 合外力矩 M 内力矩成对抵消 =0 的大小成正比， 得 与刚体的转动惯量 M= ∑ ri b 成反比。
刚体转动及角动量守恒
刚体运动的分类 刚体：形状固定的质点系（含无数质点、不形变、理想固体。）
平 动 定轴转动 平面运动 定点运动 一般运动
刚体任意 刚体质心 刚体每点 限制在一平 两点的连线 保持方向不 绕同一轴线 面内，转轴 变。各点的 作圆周运动， 可平动，但 且转轴空间 始终垂直于 位置及方向 该平面且通 相同，可当 不变。 过质心 作质点处理。
刚 体 公式对比 角位移
的 定 轴 转 动
位移 速度
加速度 匀速直线运动 匀变速直线运动
角速度
角加速度 匀角速定轴转动 匀变角速定轴转动
刚体转动定律引言
质点
或
刚体平动 的运动定律
F = ma
合外力
惯性质量
合加速度
若刚体作定轴转动，服从怎样的运动定律？
主要概念 使刚体产生转动效果的合外力矩 刚体的转动定律 刚体的转动惯量
O
ji
ri
等式两边乘以 i 即 并对所有质元及其所受力矩求和
sin j i + f i sin q i Fi刚体的转动定律 = a it = ri b
受外力 b fi ∑ Fii 受内力 ai Fi + f i = 与刚体性质及质量分布有 其法向 n 分量均通过转轴， 关的物理量，用 I 表示 不产生转动力矩。 称为 t 转动惯量 投影式为 其切向
合外力矩
M1
外力在转动平面上对转 轴的力矩使刚体发生转动
F2
Ft 2
j2
r2
P2
O
r1
F t1
P1
F1
j1
d2 d1
力矩 M1 = r1 × F1 大小 M1 = r1 F1 sin j1 方向
M2
合外力矩 大小
大小
M = M1 + M 2
= F1 d 1 = Ft 1 r1 M M 2 = r 2 × F2 M 2 = r 2F 2 sin j 2 F 2 r2 = F2 d 2 = Ft
得
得
任意时刻的 匀变角速定轴转动的角位移方程
或
匀变角速定轴转动的运动方程
定轴转动刚体在某时刻t 的瞬时角速度为 ，瞬 时角加速度为 ， 刚体中一质点P至转轴的距离为r 瞬时线速度 的大小 质点P 瞬时切向加速度 瞬时法向加速度
线量与角量的关系
这是定轴转动中线量与角量的基本关系
质点直线运动或刚体平动