第4课时：超重与失重、临界问题

《超重与失重》讲义一、超重与失重的概念当物体具有向上的加速度时，物体对支持物的压力（或对悬挂物的拉力）大于物体所受重力的现象，称为超重；当物体具有向下的加速度时，物体对支持物的压力（或对悬挂物的拉力）小于物体所受重力的现象，称为失重。

如果物体的加速度方向竖直向下，且大小等于重力加速度 g 时，物体对支持物的压力（或对悬挂物的拉力）等于零，这种状态称为完全失重。

为了更直观地理解这两个概念，我们可以想象一个人站在体重秤上。

当人静止时，体重秤的示数等于人的重力。

当人加速上升时，体重秤的示数会大于人的重力，这就是超重现象；当人加速下降时，体重秤的示数会小于人的重力，这就是失重现象；当人自由落体时，体重秤的示数为零，这就是完全失重现象。

二、超重与失重的产生条件超重现象产生的条件是物体具有向上的加速度。

例如，当电梯加速上升时，人站在电梯里会感到脚下的支持力变大，体重秤的示数增加，这就是超重现象。

在这种情况下，根据牛顿第二定律 F mg ＝ ma，其中 F 是支持力，m 是人的质量，g 是重力加速度，a 是加速度。

因为 a向上，所以 F 大于 mg，即支持力大于重力，产生超重现象。

失重现象产生的条件是物体具有向下的加速度。

比如，当电梯加速下降时，人会感觉脚下的支持力变小，体重秤的示数减小，这就是失重现象。

此时，根据牛顿第二定律 mg F ＝ ma，因为 a 向下，所以 F小于 mg，即支持力小于重力，产生失重现象。

完全失重现象产生的条件是物体的加速度等于重力加速度且方向竖直向下。

在太空中的航天器中，宇航员就处于完全失重状态。

因为航天器绕地球做圆周运动，其向心加速度等于重力加速度，此时宇航员对航天器的压力为零。

三、超重与失重的本质超重和失重现象的本质是物体所受的合力发生了变化，从而导致物体对支持物的压力或对悬挂物的拉力发生了改变。

重力本身并没有变化，只是由于加速度的存在，使得物体的视重（即物体对支持物的压力或对悬挂物的拉力）发生了改变。

第四讲两类动力学问题超重和失重基础知识归纳1、超重与失重和完全失重（1）实重和视重①实重：物体实际所受的重力，它与物体的运动状态无关.②视重：当物体挂在弹簧测力计下或放在水平台秤上时，弹簧测力计或台秤的_示数称为视重，视重的大小等于弹簧测力计所受物体的_ 拉力_或台秤所受物体的压力。

（2）超重、失重和完全失重的比较现象实质超重物体对支持物的压力或对悬挂物的拉力大于自身重力的现象系统具有竖直向上的加速度或加速度有竖直向上的分量失重物体对支持物的压力或对悬挂物的拉力小于自身重力的现象系统具有竖直向下的加速度或加速度有竖直向下的分量完全失重物体对支持物的压力或对悬挂物的拉力等于零的现象系统具有竖直向下的加速度，且a＝g①当物体处于超重和失重状态时，物体所受的重力并没有变化.②物体是否处于超重或失重状态，不在于物体向上运动还是向下运动，而是取决于加速度方向是向上还是向下.③当物体处于完全失重状态时，重力只产生使物体具有a＝g的加速度效果，不再产生其他效果.④处于超重和失重状态下的液体浮力公式分别为F浮＝ρV排(g＋a)或F浮＝ρV排(g－a)，处于完全失重状态下的液体F浮＝0，即液体对浸在液体中的物体不再产生浮力.2、连接体问题（1）连接体两个或两个以上存在相互作用或有一定关联的物体系统称为连接体，在我们运用牛顿运动定律解答力学问题中常会遇到.（2）解连接体问题的基本方法整体法：把两个或两个以上相互连接的物体看成一个整体，此时不必考虑物体之间的内力.隔离法：当求物体之间的作用力时，就需要将各个物体隔离出来单独分析.解决实际问题时，将隔离法和整体法交叉使用，有分有合，灵活处理.（3）整体法和隔离法的应用①解答问题时，不能把整体法和隔离法对立起来，而应该把这两种方法结合起来，从具体问题的实际情况出发，灵活选取对象，恰当地选择使用隔离法和整体法.②在使用隔离法解题时，所选取的隔离对象可以是连接体中的某一个物体，也可以是连接体中的某部分物体(包含两个或两个以上的单个物体)，而这“某一部分”的选取，也应根据问题的实际情况，灵活处理.③在选用整体法和隔离法时，可依据所求的力进行选择，若为外力则应用整体法；若所求力为内力则用隔离法.但在具体应用时，绝大多数的题目要求两种方法结合应用，且应用顺序也较为固定，即求外力时，先隔离后整体；求内力时，先整体后隔离.先整体或先隔离的目的都是为了求解共同的加速度.3、整体运用牛顿第二定律应用牛顿第二定律时，若研究对象为一物体系统，可将系统的所有外力及系统内每一物体的加速度均沿互相垂直的两个方向分解，则牛顿第二定律的系统表达式为：ΣF x＝m1a1x＋m2a2x＋…＋m n a nxΣF y＝m1a1y＋m2a2y＋…＋m n a ny应用牛顿第二定律的系统表达式解题时，可不考虑系统内物体间的相互作用力(即内力)，这样能达到简化求解的目的，但需把握三个关键点：（1）正确分析系统受到的外力；（2）正确分析系统内各物体加速度的大小和方向；（3）确定正方向，建立直角坐标系，并列方程进行求解.【例1】在升降电梯内的地面上放一体重计，电梯静止时，晓敏同学站在体重计上，体重计示数为50 kg，电梯运动过程中，某一段时间内晓敏同学发现体重计示数如图所示，在这段时间内下列说法中正确的是()A．晓敏同学所受的重力变小了B．晓敏对体重计的压力小于体重计对晓敏的支持力C．电梯一定在竖直向下运动D．电梯的加速度大小为g/5，方向一定竖直向下【练习1】在箱式电梯里的台秤秤盘上放着一物体，在电梯运动过程中，某人在不同时刻拍了甲、乙和丙三张照片，如图所示，乙图为电梯匀速运动的照片。

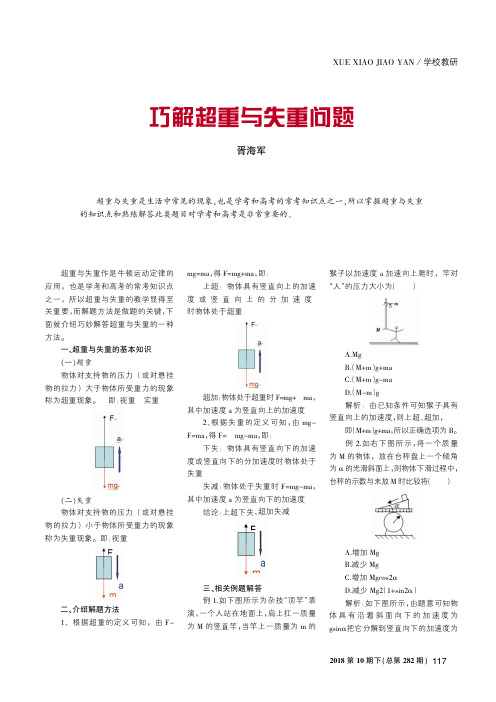
2018第10期下(总第282期)超重与失重作是牛顿运动定律的应用，也是学考和高考的常考知识点之一，所以超重与失重的教学显得至关重要，而解题方法是做题的关键，下面就介绍巧妙解答超重与失重的一种方法。

一、超重与失重的基本知识(一)超重物体对支持物的压力（或对悬挂物的拉力）大于物体所受重力的现象称为超重现象。

﹥即：视重实重(二)失重物体对支持物的压力（或对悬挂物的拉力）小于物体所受重力的现象称为失重现象。

即：视重二、介绍解题方法1、根据超重的定义可知，由F-mg=ma ，得F=mg+ma ，即：上超：物体具有竖直向上的加速度或竖直向上的分加速度时物体处于超重超加：物体处于超重时F=mg+ma ，其中加速度a 为竖直向上的加速度2、根据失重的定义可知，由mg-F=ma ，得F=mg-ma ，即：下失：物体具有竖直向下的加速度或竖直向下的分加速度时物体处于失重失减：物体处于失重时F=mg-ma ，其中加速度a 为竖直向下的加速度结论：上超下失、超加失减三、相关例题解答例1.如下图所示为杂技“顶竿”表演，一个人站在地面上，肩上扛一质量为M 的竖直竿，当竿上一质量为m 的猴子以加速度a 加速向上爬时，竿对“人”的压力大小为（）A.MgB.（M+m ）g+maC.（M+m ）g-maD.（M-m ）g解析：由已知条件可知猴子具有竖直向上的加速度，则上超、超加，即（M+m ）g+ma ，所以正确选项为B 。

例2.如右下图所示，将一个质量为M 的物体，放在台秤盘上一个倾角为α的光滑斜面上，则物体下滑过程中，台秤的示数与未放M 时比较将（）A.增加MgB.减少MgC.增加Mgcos2αD.减少Mg2（1+sin2α）解析：如下图所示，由题意可知物体具有沿着斜面向下的加速度为gsinα把它分解到竖直向下的加速度为巧解超重与失重问题胥海军超重与失重是生活中常见的现象,也是学考和高考的常考知识点之一,所以掌握超重与失重的知识点和熟练解答此类题目对学考和高考是非常重要的。

超重和失重知识点总结
超重和失重是物理学中的两个重要概念，主要涉及到重力和加速度的影响。

1. 超重：当物体受到的向上的力大于向下的重力时，物体就会处于超重状态。

这种情况下，物体的实际重量会超过其正常重量。

例如，在电梯中上升或在过山车上下降时，我们会感到身体变重，这就是超重现象。

2. 失重：当物体受到的向上的力等于向下的重力时，物体就会处于失重状态。

这种情况下，物体的实际重量为零。

例如，在飞机上自由下落或在太空中漂浮时，我们会感到身体变轻，这就是失重现象。

3. 超重和失重的区别在于向上的力和向下的重力之间的关系。

如果向上的力大于重力，就是超重；如果向上的力等于重力，就是失重；如果向上的力小于重力，就是欠重。

4. 超重和失重都是相对的，取决于观察者的参考系。

例如，在电梯中上升时，对于电梯内部的人来说，他们处于失重状态；但对于电梯外部的人来说，他们看到的是电梯内部的人处于超重状态。

5. 超重和失重的现象可以通过实验来观察和验证。

例如，可以通过离心机产生离心力来实现超重和失重的状态。

《超重与失重》讲义一、超重与失重的概念在我们的日常生活中，物体的重量似乎是一个恒定不变的量。

但当我们深入研究物体的运动状态时，会发现物体所受的重力在某些情况下会发生变化，这就引出了超重和失重的概念。

超重，简单来说，就是物体对支持物的压力（或对悬挂物的拉力）大于物体所受重力的现象。

而失重，则是物体对支持物的压力（或对悬挂物的拉力）小于物体所受重力的现象。

要理解这两个概念，我们需要先明确重力的本质。

重力是由于地球对物体的吸引而产生的力，其大小通常用公式 G ＝ mg 来计算，其中m 是物体的质量，g 是重力加速度，约为 98 米每秒平方。

二、超重的情况当物体具有向上的加速度时，就会出现超重现象。

例如，在电梯加速上升的过程中。

假设一个人的质量为 60 千克，正常情况下，他所受的重力为 60×98 ＝ 588 牛。

当电梯以加速度 a 向上加速运动时，根据牛顿第二定律 F G ＝ ma，此时人对电梯地板的压力 F 就等于重力 G 加上 ma。

如果加速度 a 为 2 米每秒平方，那么 ma 就是 60×2 ＝ 120 牛，压力 F 就等于 588 ＋ 120 ＝ 708 牛。

显然，此时人对电梯地板的压力大于自身重力，处于超重状态。

再比如，在火箭发射时，宇航员会经历强烈的超重。

火箭加速升空，加速度极大，宇航员所受的支持力远大于自身重力，会感到身体沉重，甚至呼吸困难。

三、失重的情况与超重相反，当物体具有向下的加速度时，就会出现失重现象。

最常见的例子是电梯加速下降。

还是以刚才那个人为例，如果电梯以加速度 2 米每秒平方向下加速运动，此时人对电梯地板的压力 F 就等于重力 G 减去 ma，即 588 120 ＝ 468 牛，小于自身重力，处于失重状态。

在太空中的航天器绕地球做圆周运动时，也处于失重状态。

此时，航天器和里面的物体所受的万有引力全部用来提供向心力，产生向心加速度，物体对航天器的压力为零，处于完全失重状态。