2015年中考数学复习资料 第八章图形的变换(3份)

中考数学《图形的变换》复习资料总结
中考数学《图形的变换》复习资料总结
考点一、平移 (3~5分)
1、定义
把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的.形状和大小完全相同，图形的这种移动叫做平移变换，简称平移。

2、性质
(1)平移不改变图形的大小和形状，但图形上的每个点都沿同一方向进行了移动
(2)连接各组对应点的线段平行(或在同一直线上)且相等。

考点二、轴对称 (3~5分)
1、定义
把一个图形沿着某条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称，该直线叫做对称轴。

2、性质
(1)关于某条直线对称的两个图形是全等形。

(2)如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。

(3)两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

3、判定
如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

4、轴对称图形
把一个图形沿着某条直线折叠，如果直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

考点三、旋转 (3~8分)
1、定义
把一个图形绕某一点O转动一个角度的图形变换叫做旋转，其中O叫做旋转中心，转动的角叫做旋转角。

2、性质
(1)对应点到旋转中心的距离相等。

图形与图形的变换1．图形的初步认识①掌握画基本几何体(直棱柱、圆柱、圆锥、球)的三视图，会判断简单物体的三视图，能根据三视图描述基本几何体或实物原型．②了解直棱柱、圆锥的侧面展开图，能根据展开图判断立体模型．③了解几何体与其三视图、展开图(球除外)之间的关系．④掌握比较角的大小，估计一个角的大小，计算角度的和与差，进行度、分、秒简单换算．⑤了解角平分线及其性质，了解补角、余角、对顶角；理解等角的余角相等、等角的补角相等、对顶角相等．⑥了解两点之间，线段最短；了解经过两点有一条直线，并且只有一条直线．⑦了解垂线、垂线段等概念，垂线段最短的性质，点到直线距离的意义；了解过一点有且仅有一条直线垂直于已知直线．⑧掌握用三角尺或量角器过一点画一条直线的垂线；了解线段垂直平分线及其性质．⑨理解平行线的特征和平行线的识别；了解过直线外一点有且仅有一条直线平行于已知直线；掌握用三角尺和直尺过已知直线外一点画这条直线的平行线．⑩理解平行线之间距离的意义；掌握度量两条平行线之间的距离的方法．2．轴对称①认识轴对称．②理解对应点所连的线段被对称轴垂直平分的性质．③掌握能按要求作简单平面图形经过一次或两次轴对称后的图形．④掌握简单图形之间的轴对称关系，并指出对称轴．⑤掌握基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性质及相关性质．⑥掌握利用轴对称进行图案的设计．3．平移和旋转①认识平移，理解对应点连线平行且相等的性质；掌握按要求作简单平面图形平移后的图形；掌握选用平移进行图案设计．②认识旋转(含中心对称)；理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质．③了解平行四边形、圆是中心对称图形．④掌握按要求作简单平面图形旋转后的图形．⑤掌握图形之间的轴对称、平移、旋转及其组合四种关系形式．⑥掌握运用轴对称、平移和旋转的组合进行图案设计．⑦在观察、操作、推理、归纳等探索过程中，发展学生的合情推理能力，培养学生的数学说理的习惯与能力．【课时分布】图形与图形的变换在第一轮复习时大约需要3个课时，下表为内容及课时安排(仅供参考)课时数内容1基本图形的认识1轴对称与轴对称图形1平移与旋转1图形与图形的变换单元测试与评析【知识回顾】1．知识脉络图形的初步认识立体图形平面图形视图平面展开图点和线角相交线平行线图形之间的变换关系轴对称平移旋转旋转对称中心对称2．基础知识(1)两点之间线段最短；连结直线外一点与直线上各点的所有线段中，垂线段最短．(2)视图有正视图、俯视图、侧视图(左视图、右视图)．(3)平行线间的距离处处相等．(4)平移是由移动的方向和距离决定的．(5)平移的特征：①对应线段平行(或共线)且相等；连结对应的线段平行(或共线)且相等；②对应角分别相等；③平移后的图形与原图形全等．(6)图形的旋转由旋转中心、旋转角度和旋转方向决定．(7)旋转的特征：①对应点与旋转中心的距离相等；对应线段相等，对应角相等；②每一点都绕旋转中心旋转了相同的角度；③旋转后的图形与原图形全等．3、能力要求例1选择、填空题(1)如图6-1，小军将一个直角三角板绕它的一条直角边所在的直线旋转一周形成一个几何体，将这个几何体的侧面展开得到的大致图形是·····································Ａ．B．C ．D ．【分析】图形的旋转与展开．【解】D ．(2)如图6-2，已知□ABCD 的对角线BD =4cm ，将□ABCD 绕其对称中心O 旋转180°，则点D 所转过的路径长为（）A ．4πcmB ．3πcmC ．2πcmD ．πcm【分析】图形的旋转与圆弧问题结合．【解】C ．(3)有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O 按逆时针方向进行旋转，每次均旋转45 ，第1次旋转后得到图①，第2次旋转后得到图②……，则第10次旋转后得到的图形与图①～图④中相同的是（）A ．图①B ．图②C ．图③D ．图④【分析】图形的旋转与操作．【解】B ．(4)如图6-3，在Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，ABCD 图6-3C’图①图②图③图④图6-2ABCDO图6-1(5)按图中所示方法将△BCD 沿BD 折叠，使点C 落在边AB 上的点C ′处，则折痕BD的长为__________．【分析】图形的折叠与勾股定理应用．【解】35．(5)如图6-4，在68⨯的网格图（每个小正方形的边长均为1个单位长度）中，⊙A 的半径为2个单位长度，⊙B 的半径为1个单位长度，要使运动的⊙B 与静止的⊙A 内切，应将⊙B 由图示位置向左平移个单位长度．【分析】图形平移、圆的位置关系与发散思维结合【解】4或6(6)如图6-5所示，在折纸活动中，小明制作了一张ABC △纸片，点D E 、分别是边AB 、AC 上，将ABC△沿着DE 折叠压平，A 与'A 重合，若=70A ︒∠，则1+2∠∠=（）A.140︒B.130︒C.110︒D.70︒【分析】图形折叠、三角形内角和与平角的结合【解】A(7)如图6-6-1和6-6-2，四边形ABCD 是边长为1的正方形，四边形EFGH 是边长为2的正方形，点D 与点F 重合，点B ，D （F ），H 在同一条直线上，将正方形ABCD 沿F →H 方向平移至点B 与点H 重合时停止，设点D 、F 之间的距离为x ，正方形ABCD 与正方形EFGH 重叠部分的面积为y ，则能大致反映y 与x 之间函数关系的图象是（）图6-4图6-5图图【分析】图形的平移、动点问题及函数图像【解】B【说明】由于概念、性质比较多，复习时可以通过基本练习题的训练，使学生熟练掌握图形与图形变换的基本知识、基本方法和基本技能．重视平移、旋转、折叠、展开过程中学生思维的训练，重视平移、旋转、折叠、展开的操作过程，提高学生的分解、组合图形的能力和动手能力。

第八章图形与变换课时25．视图与投影【考点链接】1. 从观察物体时，看到的图叫做主视图；从观察物体时，看到的图叫做左视图；从观察物体时，看到的图叫做俯视图.2. 主视图与俯视图的一致；主视图与左视图的一致；俯视图与左视图的一致.3. 叫盲区.4. 投影可分为平行投影与中心投影.其中所形成的投影叫平行投影；所形成的投影叫中心投影.5. 利用光线是否平行或是否交于一点来判断是投影或投影，以及光源的位置和物体阴影的位置.【河北三年中考试题】1.（2009年，2分）从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图5所示的零件，则这个零件的表面积是（）A．20 B．22图5 C．24 D．26课时26．轴对称与中心对称【考点链接】1. 如果一个图形沿一条直线对折，对折后的两部分能 ，那么这个图形就是 ，这条直线就是它的 .2. 如果一个图形沿一条直线折叠，如果它能与另一个图形 ，那么这两个图形成 ，这条直线就是 ，折叠后重合的对应点就是 。

3. 如果两个图形关于 对称，那么对称轴是任何一对对应点所连线段的 .4. 把一个图形绕着某一个点旋转 °，如果旋转后的图形能够与原来的图形 ，那么这个图形叫做 图形，这个点就是它的 ．5. 把一个图形绕着某一个点旋转 °，如果它能够与另一个图形 ，那么就说这两个图形关于这个点 ，这个点叫做 ．这两个图形中的对应点叫做关于中心的 ．6. 关于中心对称的两个图形，对称点所连线段都经过 ，而且被对称中心所 ．关于中心对称的两个图形是 图形.7. 两个点关于原点对称时，它们的坐标符号 ，即点),(y x P 关于原点的对称点1P 为 .【河北三年中考试题】1.（2008年，10分）在一平直河岸同侧有两个村庄，到的距离分别是3km 和2km ，．现计划在河岸上建一抽水站，用输水管向两个村庄供水． 方案设计某班数学兴趣小组设计了两种铺设管道方案：图13-1是方案一的示意图，设该方案中管道长度为，且（其中于点）；图13-2是方案二的示意图，设该方案中管道长度为，且（其中点与点关于对称，与交于点）．观察计算（1）在方案一中， km （用含的式子表示）；（2）在方案二中，组长小宇为了计算的长，作了如图13-3所示的辅助线，请你按小宇同学的思路计算， km （用含的式子表示）． 探索归纳（1）①当时，比较大小：（填“＞”、“＝”或“＜”）； ①当时，比较大小：（填“＞”、“＝”或“＜”）； （2）请你参考右边方框中的方法指导， 就（当时）的所有取值情况进 行分析，要使铺设的管道长度较短， 应选择方案一还是方案二？l A B ，A B ，l km AB a =(1)a >l P 1d 1(km)d PB BA =+BP l ⊥P 2d 2(km)d PA PB =+A 'A l A B 'l P 1d =a 2d 2d =a 4a =12_______d d 6a =12_______d d a 1a >AB P llAB PC 图13-1 图13-2lA B PC 图13-3K 方法指导当不易直接比较两个正数与的大小时，可以对它们的平方进行比较：，，与的符号相同．当时，，即； 当时，，即； 当时，，即；课时27．平移与旋转【考点链接】1. 一个图形沿着一定的方向平行移动一定的距离，这样的图形运动称为______，它是由移动的和所决定．2. 平移的特征是：经过平移后的图形与原图形的对应线段，对应，图形的与都没有发生变化，即平移前后的两个图形；且对应点所连的线段．3. 图形旋转的定义：把一个图形的图形变换，叫做旋转，叫做旋转中心，叫做旋转角．4. 图形的旋转由、和所决定．其中①旋转在旋转过程中保持不动．①旋转分为时针和时针. ①旋转一般小于360º.5. 旋转的特征是：图形中每一点都绕着旋转了的角度，对应点到旋转中心的相等，对应相等，对应相等，图形的都没有发生变化.也就是旋转前后的两个图形.【河北三年中考试题】 1．（2008年，2分）有一个四等分转盘，在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌，如图5-1．若将位于上下位置的两个字牌对调，同时将位于左右位置的两个字牌对调，再将转盘顺时针旋转，则完成一次变换．图5-2，图5-3分别表示第1次变换和第2次变换．按上述规则完成第9次变换后，“众”字位于转盘的位置是（ ）A ．上B ．下C ．左D ．右2．（2008年，10分）如图14-1，的边在直线上，，且；的边也在直线上，边与边重合，且．（1）在图14-1中，请你通过观察、测量，猜想并写出与所满足的数量关系和位置关系；（2）将沿直线向左平移到图14-2的位置时，交于点，连结，．猜想并写出与所满足的数量关系和位置关系，请证明你的猜想；（3）将沿直线向左平移到图14-3的位置时，的延长线交的延长线于点，连结，．你认为（2）中所猜想的与的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．3．（2010年，2分）将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图6-1．在图6-2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图6-1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是（ ）A ．6B ．5C ．3D ．290ABC △BC l AC BC ⊥AC BC =EFP △FP l EF AC EF FP =AB AP EFP △l EP AC Q AP BQ BQ AP EFP △l EP AC Q AP BQ BQ AP 众 志成 城图5-1 成 城众志图5-2 志 成城 众第1次变换 城 众志成图5-3 成 城众志第2次变换…A （E ） BC （F ） P lllA AB BQPEFFC Q图14-1图14-2图14-3E PC图6-1 图6-2向右翻滚90° 逆时针旋转90°。

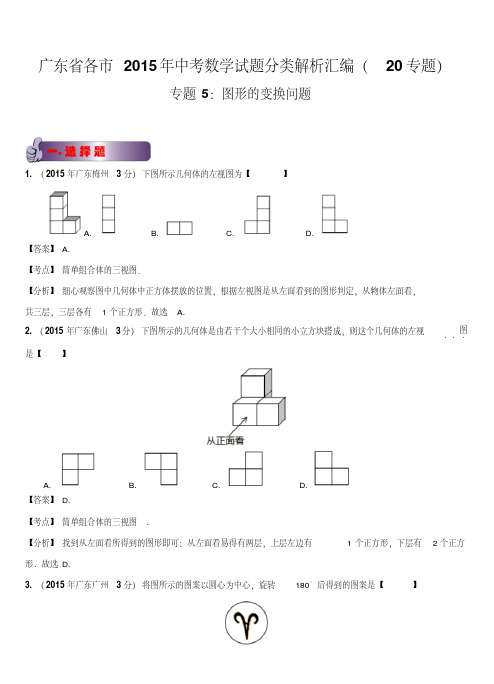
广东省各市2015年中考数学试题分类解析汇编（20专题）专题5：图形的变换问题1. （2015年广东梅州3分）下图所示几何体的左视图为【】A. B. C. D.【答案】A.【考点】简单组合体的三视图．【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定，从物体左面看，共三层，三层各有1个正方形．故选 A.2. （2015年广东佛山3分）下图所示的几何体是由若干个大小相同的小立方块搭成，则这个几何体的左视．．图．是【】A. B. C. D.【答案】D.【考点】简单组合体的三视图.【分析】找到从左面看所得到的图形即可：从左面看易得有两层，上层左边有1个正方形，下层有2个正方形. 故选D.3. （2015年广东广州3分）将图所示的图案以圆心为中心，旋转180°后得到的图案是【】A. B. C. D.【答案】D.【考点】旋转的性质.【分析】根据旋转的性质，将图所示的图案以圆心为中心，旋转180°后得到的图案与原图形中心对称，它是.故选D.4. （2015年广东广州3分）如图是一个几何体的三视图，则这几何体的展开图可以是【】A. B. C. D.【答案】A.【考点】由三视图判断几何体；几何体的展开图.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，由于俯视图为圆形可得为球、圆柱、圆锥．主视图和左视图为矩形可得此几何体为圆柱.圆柱的展开图是一个矩形两个圆形.故选A.5. （2015年广东深圳3分）下列主视图正确的是【】A. B. C. D.【答案】A.【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可：从正面看易得有两层，上层中间有1个正方形，下层有3个正方形. 故选A.6. （2015年广东深圳3分）如图，已知正方形ABCD 的边长为12，BE =EC ，将正方形边CD 沿DE 折叠到DF ，延长EF 交AB 于G ，连接DG ，现在有如下4个结论：①ADG FDG ≌；②2GBAG ；③GDE BEF ∽；④725BEFS .在以上4个结论中，正确的有【】A. 1B. 2C.3D. 4【答案】C.【考点】折叠问题；正方形的性质；全等、相似三角形的判定和性质；勾股定理.【分析】由折叠和正方形的性质可知，,90DF DC DA DFC C ，∴90DFG A .又∵DG DG ，∴ADG FDG HL ≌. 故结论①正确.∵正方形ABCD 的边长为12，BE=EC ，∴6BE EC EF .设AGFG x ，则6,12EG x BG x ，在Rt BEG 中，由勾股定理，得222EGBEBG ，即222662xx，解得，4x . ∴4,8AG GF BG .∴2GBAG . 故结论②正确.∵6BE EF，∴BEF 是等腰三角形.易知GDE 不是等腰三角形，∴GDE 和BEF 不相似. 故结论③错误.∵11682422BEGS BE BG ，∴67224105BEFBEGEFSSEG.故结论④正确.综上所述，4个结论中，正确的有①②④三个.故选C.7. （2015年广东3分）如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD 变形为以A 为圆心，AB 为半径的扇形(忽略铁丝的粗细)，则所得的扇形DAB的面积为【】A.6B.7C. 8D. 9【答案】D.【考点】正方形的性质；扇形的计算.【分析】∵扇形DAB的弧长?DB等于正方形两边长的和6BC CD，扇形DAB的半径为正方形的边长3，∴16392扇形DABS.或由变形前后面积不变得：339正方形扇形ABCDDABS S.故选D.8. （2015年广东汕尾4分）下图所示几何体的左视图为【】A. B. C. D.【答案】A.【考点】简单组合体的三视图．【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定，从物体左面看，共三层，三层各有1个正方形．故选 A.9. （2015年广东汕尾4分）如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为【】A. 25B. 5C. 455D.255【答案】B.【考点】折叠问题；矩形的性质；折叠对称的性质；菱形的判定和性质；勾股定理；方程思想的应用.【分析】如答图，连接,AF CE ，设AC 与EF 相交于点O .则根据折叠和矩形的性质得，四边形AECF 是菱形，∴AECE .∵04290AB BC B ，，，∴222425AC.∴5AO .设AE CEx ，则4BEx . ∵222CEBEBC ，∴22242x x，得52x.∴在Rt AOE 中，222255522OE AEAO.∴5EF .故选B.1. （2015年广东梅州3分）如图，将矩形纸片ABCD 折叠，使点A 与点C 重合，折痕为EF ，若AB=4，BC=2，那么线段EF 的长为▲　..【答案】5.【考点】折叠问题；矩形的性质；折叠对称的性质；菱形的判定和性质；勾股定理；方程思想的应用.【分析】如答图，连接,AF CE ，设AC 与EF 相交于点O .则根据折叠和矩形的性质得，四边形AECF 是菱形，∴AECE .∵04290AB BC B ，，，∴222425AC.∴5AO .设AE CEx ，则4BEx . ∵222CEBEBC ，∴22242x x，得52x.∴在Rt AOE 中，222255522OEAEAO.∴5EF .2. （2015年广东广州3分）如图，四边形ABCD中，∠A=90°，33AB，AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为▲　.【答案】3.【考点】双动点问题；三角形中位线定理；勾股定理.【分析】如答图，连接DN，∵点E，F分别为DM，MN的中点，∴12EF DN.∴要使EF最大，只要DN最大即可.根据题意，知当点N到达点B与B重合时，DN最大. ∵∠A=90°，33AB，AD=3，∴223336DN DB，此时，132EF DN.3. （2015年广东深圳3分）观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有▲　个太阳.【答案】21.【考点】探索规律题（图形的变化类）.【分析】观察图形可知，上面一排按序号1，2，3，4，,排列，第5个图形有5个太阳；下面一排按012342,2,2,2,2,排列，第5个图形有4216个太阳；∴第5个图形共有21个太阳.4. （2015年广东珠海4分）用半径为12cm，圆心角为90°的扇形纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为▲　cm ．【答案】3．【考点】圆锥和扇形的计算．【分析】根据题意，得扇形的弧长为：90126180鬃=，∵圆锥的底面周长等于它的侧面展开图的弧长，∴根据圆的周长公式，得26r =，解得3r =．∴圆锥的底面半径为3cm ．1. （2015年广东梅州10分）在Rt △ABC 中，∠A=90°，AC = AB = 4，D ，E 分别是边AB ，AC 的中点.若等腰Rt △ADE 绕点A 逆时针旋转，得到等腰Rt △AD 1E 1，设旋转角为α（0＜α≤180°），记直线BD 1与CE 1的交点为P.（1）如图1，当α=90°时，线段BD 1的长等于▲　，线段CE 1的长等于▲　；（直接填写结果）（2）如图2，当α=135°时，求证：BD 1 = CE 1 ，且BD 1⊥CE 1 ；（3）求点P 到AB 所在直线的距离的最大值．（直接写出结果）【答案】解：（1）25，25.（2）证明：当α=135°时，由旋转可知∠D 1AB =E 1AC = 135°. 又∵AB=AC ，AD 1=AE 1，∴△D 1AB ≌△△E 1AC （SAS ）. ∴BD 1=CE 1且∠D 1BA = ∠E 1CA.设直线BD 1与AC 交于点F ，有∠BFA=∠CFP . ∴∠CPF=∠FAB=90°，∴BD 1⊥CE 1. （3）13.【考点】面动旋转问题；等腰直角三角形的性质；勾股定理；全等、相似三角形的判定和性质.【分析】（1）如题图1，当α=90°时，线段BD 1的长等于22224225ABAE；线段CE 1的长等于222214225ACAE .（2）由SAS 证明△D 1AB ≌△△E 1AC 即可证明BD 1 = CE 1 ，且BD 1⊥CE 1 . （3）如答图2，当四边形AD 1PE 1为正方形时，点P 到AB 所在直线的距离距离最大，此时112223AD PD PB，，∵1ABD PBH ∽，∴1AD AB PHPB.∴24223PH.∴13PH .∴当四边形AD 1PE 1为正方形时，点P 到AB 所在直线的距离距离的最大值为13.2. （2015年广东深圳9分）如图1，水平放置一个三角板和一个量角器，三角板的边AB 和量角器的直径DE在一条直线上，,3,6cm OD cm BC AB 开始的时候BD=1cm ，现在三角板以2cm/s 的速度向右移动.（1）当B 与O 重合的时候，求三角板运动的时间；（2）如图2，当AC 与半圆相切时，求AD ；（3）如图3，当AB 和DE 重合时，求证：2CFCG CE .【答案】解：（1）∵开始时，4BO cm ，三角板以2cm/s 的速度向右移动，∴当B 与O 重合的时候，三角板运动的时间为422/cm s cm s. （2）如答图1，设AC 与半圆相切于点H ，连接OH ，则OHAC .∵,90AB BC ABC ，∴45A .又∵3OH OD cm ，∴232AO OH .∴323ADAODOcm .（3）如答图2，连接EF ，∵OD OF，∴ODF OFD.∵DF是直径，∴090DFE. ∴090ODF DEF. 又∵090DEC DEF CEF.∴ODF CEF. ∴CFG OFD ODF CEF.又∵FCG ECF，∴CFG CEF∽.∴CF CECG CF，即2CF CG CE.【考点】面动平移问题；等腰（直角）三角形的判定和性质；圆周角定理；相似三角形的判定和性质.【分析】（1）直接根据“路程时间速度”计算即可.（2）作辅助线“连接O与切点H”，构成等腰直角三角形求出AO的长，从而由AO DO求出AD 的长.（3）作辅助线“连接EF”，构成相似三角形CFG CEF∽,得比例式即可得解.3.（2015年广东7分）如题图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长交BC于点G，连接AG.（1）求证：△ABG≌△AFG；（2）求BG的长.【答案】解：（1）∵四边形ABCD是正方形，∴∠B=∠D=90°，AD=AB.由折叠的性质可知，AD=AF，∠AFE=∠D=90°，∴∠AFG=90°，AB=AF.∴∠AFG=∠B.又∵AG=AG，∴△ABG≌△AFG（HL）.（2）∵△ABG≌△AFG，∴BG=FG.设BG=FG=x，则GC=6x,∵E为CD的中点，∴CF=EF=DE=3，∴EG=3x，在Rt CEG 中，由勾股定理，得2223(6)(3)x x ，解得2x，∴BG=2.【考点】折叠问题；正方形的性质；折叠对称的性质；全等三角形的判定和性质；勾股定理；方程思想的应用.【分析】（1）根据正方形和折叠对称的性质，应用HL 即可证明△ABG ≌△AFG （HL ）.（2）根据全等三角形的性质，得到BG=FG ，设BG=FG =x ，将GC 和EG 用x 的代数式表示，从而在Rt CEG 中应用勾股定理列方程求解即可.4. （2015年广东汕尾11分）在Rt △ABC 中，∠A=90°，AC = AB = 4，D ，E 分别是边AB ，AC 的中点.若等腰Rt △ADE 绕点A 逆时针旋转，得到等腰Rt △AD 1E 1，设旋转角为α（0＜α≤180°），记直线BD 1与CE 1的交点为P.（1）如图1，当α=90°时，线段BD 1的长等于▲　，线段CE 1的长等于▲　；（直接填写结果）（2）如图2，当α=135°时，求证：BD 1 = CE 1 ，且BD 1⊥CE 1 ；（3）求点P 到AB 所在直线的距离的最大值．（直接写出结果）【答案】解：（1）25，25.（2）证明：当α=135°时，由旋转可知∠D 1AB =E 1AC = 135°. 又∵AB=AC ，AD 1=AE 1，∴△D 1AB ≌△△E 1AC （SAS ）. ∴BD 1=CE 1且∠D 1BA = ∠E 1CA.设直线BD 1与AC 交于点F ，有∠BFA=∠CFP . ∴∠CPF=∠FAB=90°，∴BD 1⊥CE 1. （3）13.【考点】面动旋转问题；等腰直角三角形的性质；勾股定理；全等、相似三角形的判定和性质.【分析】（1）如题图1，当α=90°时，线段BD 1的长等于22224225ABAE；线段CE 1的长等于222214225AC AE .（2）由SAS 证明△D 1AB ≌△△E 1AC 即可证明BD 1 = CE 1 ，且BD 1⊥CE 1 .（3）如答图2，当四边形AD 1PE 1为正方形时，点P 到AB 所在直线的距离距离最大，此时112223AD PD PB ，，∵1ABD PBH ∽，∴1AD ABPH PB .∴24223PH .∴13PH .∴当四边形AD 1PE 1为正方形时，点P 到AB 所在直线的距离距离的最大值为13.5. （2015年广东珠海7分）已知,ABC AB AC D =，将ABC D 沿BC 方向平移得到DEF D ．（1）如图1，连接,BD AF ，则BD ▲　AF （填“>”，“<”或“=”号）；（2）如图2，M 为AB 边上一点，过M 作BC 的平行线MN 分别交边,,AC DE DF 于点,,G H N ，连接,BH GF ．求证：BH GF =．【答案】解：（1）=.（2）证明：∵将ABC D 沿BC 方向平移得到DEF D ，MN ∥AB ，∴根据平移的性质，得,,MG HN GC NF MGC HNF ==?.∵AB AC =，∴ABC ACB ?.又∵MN ∥AB ，∴四边形BCGM 是等腰梯形.∴,MB GC GMB MGC =?.∴,MB MF GMB HNF =?.又∵MG HN =，∴MH GN =.在BMH D 和FNG D 中，∵,,MB MF HMB GNF MH NG =??，∴BMH D ≌()FNG SAS D .∴BH GF =．【考点】面动平移问题；平移的性质，平行的性质；等腰梯形的判定和性质；全等三角形的判定和性质. 【分析】（1）根据平移的性质，应用SAS 证明ABF D ≌DFB D 即可得出BD AF =的结论.（2）根据平移的性质，结合等腰梯形的判定和性质，应用SAS 证明BMH D ≌FNG D 即可得出BH GF =的结论.。

一、选择题：1. (2015.河北省，第3题，3分)一张菱形纸片按图1-1、图1-2依次对折后.再按图l-3打出一个圆形小孔，则展开铺平后的图案是（ ）A.B. C. D.【答案】C 【解析】试题分析：采用逆向思维的方法，如下图：故选：C考点: 轴对称，折叠问题2．(2015.安徽省，第4题，4分)下列几何体中，俯视图是矩形的是（ ）【答案】B. 【解析】试题分析：选项A 、D 的俯视图是圆，选项B 的俯视图是矩形，选项C 的俯视图是三角形，故答案选B.考点：几何体的俯视图.3. (2015.河北省，第5题，3分)图中的三视图所对应的几何体是（ ）A ．B ．C ．D ．4.（2015.河南省，第2题，3分）如图所示的几何体的俯视图是（ ）.5．(2015.宁夏，第3题，3分)如图，放置的一个机器零件(图1)，若其主视图如(图2)所示，则其俯视图为（ ）【答案】D. 【解析】试题分析：几何体的俯视图是从上面看到的图形，这个几何体从上面看是并排的三个矩形，故答案C DB A 正面 第2题选D.考点：几何体的三视图.6.（2012.重庆市A卷，第2题，4分）下列图形是轴对称图形的是（）A．B．C． D7. （2015.重庆市B卷，第2题，4分）下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是( )A． B． C．D．8. (2015.天津市，第3题，3分)在一些美术字中，有的汉字是轴对称图形,下面4个汉字中，可以看作是轴对称图形的是( )吉祥如意（A）（B）（C）（D）9. (2015.天津市，第5题，3分)右图是一个由4个相同的正方体组成的立体图形，它的主视图是( )（A）（B）（C）（D）【答案】A.【解析】试题分析：观察几何体可得，这个几何体的主视图是四个正方形组成，故答案选A.考点：几何体的主视图.10. (2015.天津市，第11题，3分)如图，已知在ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′.若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为( )（A）130°（B）150°（C）160°（D）170°E'A'EBDC A【答案】C.11.(2015.北京市，第4题，3分)剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（ ）A.B. C. D.【答案】D ． 【解析】试题分析：在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，则这个图形叫轴对称图形；D 符合轴对称图形的定义，故选D. 考点：轴对称图形12. (2015.陕西省，第2题，3分)如图是一个螺母的示意图，它的俯视图是（ ）【答案】B ． 【解析】试题分析：根据俯视图的定义，找出从上往下看到的图形，从上往下看，俯视图为一矩形，靠近右侧有一看得见的竖直线. 故选B ．考点：简单组合体的三视图．.二、填空题：1.(2015.上海市，第18题，4分)已知在ABC ∆中，8AB AC ==，30BAC ∠=．将ABC ∆绕点A 旋转，使点B 落在原ABC ∆的点C 处，此时点C 落在点D 处．延长线段AD ，交原ABC ∆的边BC 的延长线于点E ，那么线段DE 的长等于___________．2.(2015.宁夏，第13题，3分)如图，在平面直角坐标系中，点A 的坐标为（0,4），△OAB 沿x 轴向右平移后得到△O 'A 'B '，点A 的对应点A '是直线45y x =上一点，则点B 与其对应点B '间的距离为 ．【答案】5. 【解析】试题分析：由点A 的坐标为（0,4），△OAB 沿x 轴向右平移后得到△O 'A 'B '，点A 的对应点A ',所以点A '的纵坐标为4，把y=4代入45y x =可得x=5，即OO '=5.根据平移的性质可得BB '=OO '=5,即点B 与其对应点B '间的距离为5.考点：平移的性质；正比例函数图象上点的特征.3.(2015.宁夏，第14题，3分)如图，在矩形ABCD 中，AB =3,BC =5,在CD 上任取一点E ，连接BE ,将△BCE 沿BE 折叠，使点E 恰好落在AD 边上的点F 处，则CE 的长为 ．4.（2015.重庆市A 卷，第18题，4分）如图，在矩形ABCD 中，AB=46,AD=10,连接BD ，∠DBC 的角平分线BE 交DC 于点E ，现把△BCE 绕点B 逆时针旋转，记旋转后的△BCE 为△BC E ''.当射线BE '和射线BC '都与线段AD 相交时，设交点分别F,G.若△BFD 为等腰三角形，则线段DG 长为.【答案】1798. 【解析】试题分析：此题为几何综合题，难度较大.通常与勾股定理、相似三角形相关.由题意易得∠DBC=∠DBF ，加上∠C 为直角，18题图三、解答题：1．(2015.安徽省，第17题，8分)如图，在边长为1个单位长度的小正方形网格中，给出了△ABC(顶点是网格线的交点)．(1)请画出△ABC关于直线l对称的△A1B1C1；(2)将线段AC向左平移3个单位，再向下平移5个单位，画出平移得到的线段A2C2，并以它为一边作一个格点△A2B2C2，使A2B2＝C3B2．A BCl第17题图。

中考数学复习专项知识总结—图形的变换（中考必备）1、平移(1)定义：把一个图形沿着某一直线方向移动，这种图形的平行移动，简称为平移。

(2)平移的性质：平移后的图形与原图形全等；对应角相等；对应点所连的线段平行(或在同一条直线上)且相等。

(3)坐标的平移：点（x，y）向右平移a个单位长度后的坐标变为（x+a，y）；点（x，y）向左平移a个单位长度后的坐标变为（x-a，y）；点（x，y）向上平移a个单位长度后的坐标变为（x，y+a）；点（x，y）向下平移a个单位长度后的坐标变为（x，y-a）。

2、轴对称(1)轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称。

这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点。

(2)轴对称图形：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形。

这条直线叫做它的对称轴。

(3)轴对称的性质：关于某条直线对称的图形是全等形。

经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

(4)线段垂直平分线的性质线段垂直平分线上的点到这条线段两个端点的距离相等；与一条线段两个端点距离相等的点，在线段的垂直平分线上。

(5)坐标与轴对称：点（x，y）关于x轴对称的点的坐标是（x，-y）；点（x，y）关于y轴对称的点的坐标是（-x，y）；3、旋转(1)旋转定义：把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转。

点O叫做旋转中心，转动的角叫做旋转角。

如果图形上的点P经过旋转变为点P′，那么这两个点叫做这个旋转的对应点。

旋转的性质：①对应点到旋转中心的距离相等；①对应点与旋转中心所连线段的夹角等于旋转角；①旋转前后的图形全等。

(2)中心对称定义：把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称。