【附答案或解析】2018秋九年级数学上册19.3+平行线分三角形两边成比例课堂导学

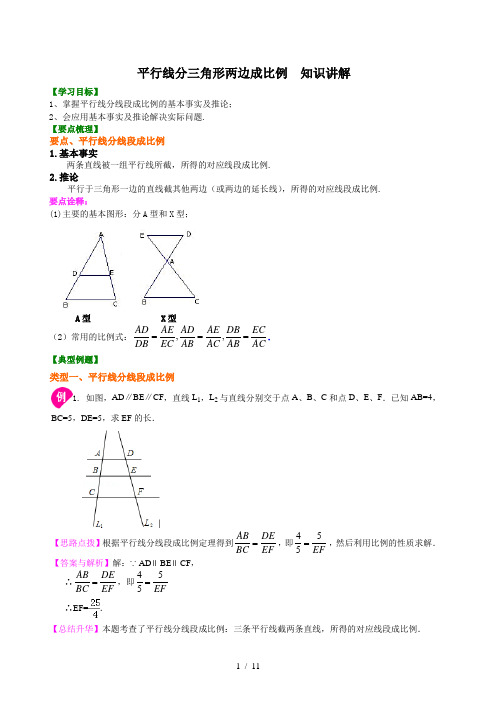
平行线分三角形两边成比例 知识讲解【学习目标】1、掌握平行线分线段成比例的基本事实及推论；2、会应用基本事实及推论解决实际问题. 【要点梳理】要点、平行线分线段成比例 1.基本事实两条直线被一组平行线所截，所得的对应线段成比例.2.推论平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例. 要点诠释：(1)主要的基本图形：分A 型和X 型；A 型 X 型 （2）常用的比例式：,,AD AE AD AE DB ECDB EC AB AC AB AC===. 【典型例题】类型一、平行线分线段成比例1. 如图，AD ∥BE ∥CF ，直线L 1，L 2与直线分别交于点A 、B 、C 和点D 、E 、F ．已知AB=4，BC=5，DE=5，求EF 的长．【思路点拨】根据平行线分线段成比例定理得到AB DE BC EF =，即455EF=，然后利用比例的性质求解． 【答案与解析】解：∵AD ∥BE ∥CF ， ∴AB DE BC EF =，即455EF= ∴EF=．【总结升华】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．举一反三【变式】如图，AD∥EF∥BC,AD=12cm，BC=18cm，AE:EB=2:3，求EF的长.【答案】解：过点D作DN∥AB,交EF于点M,交BC于点N，∵AD∥EF∥BC，∴AE DM MF AB DN NC ==∴2=518126MF MF=-,∴MF=125，即EF=EM+MF=12+125=14.4cm类型二、平行线分三角形两边成比例2. 如图已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.求证：EF：FD=CA：CB.【答案与解析】证明：过D作DK∥AB交EC于K点.则，，即又∵AD=BE ， ∴.【总结升华】运用三角形一边的平行线性质定理，即只要有平行线就可推出对应线段成比例. 举一反三【变式】如图,在⊿ABC, DG ∥EC, EG ∥BC,求证:2AE AB AD =⋅.【答案】证明：∵DG ∥EC,∴AD AGAE AC =,∵EG ∥BC,∴AE AGAB AC=, ∴AD AEAE AB=, 即2AE AB AD =⋅.3.如图，在矩形ABCD 中，AB=2，BC=3，点E 、F 、G 、H 分别在矩形ABCD 的各边上，EF ∥AC ∥HG ，EH ∥BD ∥FG ，则四边形EFGH 的周长是（ ） A.10 B.13 C.210 D.213【思路点拨】根据矩形的对角线相等，利用勾股定理求出对角线的长度，然后根据平行线分线段成比例定理列式表示出EF 、EH 的长度之和，再根据四边形EFGH 是平行四边形，即可得解．A BCD E G【答案与解析】解：在矩形ABCD 中，AB=2，BC=3，根据勾股定理，AC=BD=22AB BC +=2223+=13，∵EF ∥AC ∥HG ， ∴EF EBAC AB=， ∵EH ∥BD ∥FG ，∴EH AEBD AB=， ∴EF EH EB AEAC BD AB AB+=+=1， ∴EF+EH=AC=13，∵EF ∥HG ，EH ∥FG ，∴四边形EFGH 是平行四边形，∴四边形EFGH 的周长=2（EF+EH ）=213．故选D ．【总结升华】本题考查了平行线分线段成比例定理，矩形的对角线相等，勾股定理，根据平行线分线段成比例定理求出1EF EHAC BD+=是解题的关键，也是本题的难点． 4.（ 秋•玄武区校级期中）如图，已知点D 、F 在△ABC 的边AB 上，点E 在边AC 上，且DE ∥BC ，，求证：EF ∥DC ．【答案与解析】证明：∵DE ∥BC ，∴=， ∵=， ∴=， ∴=，∴EF ∥DC ．【总结升华】本题考查了平行线分线段成比例．注意找准对应关系，以防错解． 举一反三【变式】如图，在△ABC （AB ＞AC ）的边AB 上取一点D ，在边AC 上取一点E,使AD=AE,直线DE 和BC的延长线交于点P,求证：BP BD CP CE=.【答案与解析】证明：过点C作CF∥AB交DP于点F, ∵CF∥AB，∴∠ADE=∠EFC∵AD=AE,∴∠ADE=∠AED=∠FEC∴∠EFC=∠FEC∴CF=CE∵CF∥AB∴BP BD CP CF=,即BP BD CP CE=.5.（春•广安校级月考）如图所示，D，E是△ABC的边AB，AC上的两点，AE：AC=2：3，且AD=10，AB=15，DE=8，求BC的长．【答案与解析】解：∵AD=10，AB=15，∴AD：AB=10：15=2：3，而AE：AC=2：3，∴AE：AC=AD：AB，∴DE∥BC，∴=，即=，∴BC=12．【总结升华】此题利用平行线分线段成比例定理，找出相应线段的比值，再结合已知所给的条件，进而求出线段的长.平行线分三角形两边成比例巩固练习【巩固练习】一．选择题1. （•平房区一模）如图，如果l1∥l2∥l3，则下列各式不正确的是（）A．BC EFAC DF=B．AB EFBC DE= C．AB ACDE DF=D．AB DEAC DF=2. 如图，在△ABC中，DE∥BC，则下列比例式成立的是( )．A．B． C．D．3. 在△ABC中，点D在AB上，点E在AC上，且DE∥BC，，则等于( )．A．B．C． D．4. 如图，△ABC中，DE∥AC交AB、BC于D、E，如果AB=7cm，AC=5cm，AD=3cm，则DE=( )．A．B． C．D．5. 如图，在△ABC中，如果DE∥BC，DF∥AC，则下列比例式中不正确的是( )．A ．B ．C ．D ．6. 如图，△ABC 中，G 是BC 中点，E 是AG 中点，CE 的延长线交AB 于D ，则EC ：DE 的值为( )．A ．2B ．3C ．D ．二. 填空题7. 如图，123l l l ∥∥,BC=13AC ,DE=1.6,则EF=____________.8. 如图，DE ∥BC,BF:EF=4:3，则AC:AE=____________.9．已知点G 是△ABC 的重心，AD 是BC 边上的中线，如果GD=2cm ，那么AD=______. 10. 如图，△PMN,点A,B 分别在MP,NP 的延长线上，25AP BP AM BN ==,则MNBA=________.11.（•香坊区三模）如图，△ABC中，D、F在AB边上，E、G在AC边上，DE∥FG∥BC，且AD：DF：FB=3：2：1，若AG=15，则CE的长为.12. 如图，AD∥EF∥BC,且AE=2EB,AD=5.BC=8，则EF=_____________.三.综合题13. 如图，已知，AB∥CD∥EF，OA=14，AC=16，CE=8，BD=12，求OB、DF的长.14.（秋•平川区校级期中）已知：如图，在△ABC中，AB=AC，且，EG∥CD．证明：AE=AF．BOE FAC D15. 已知：如图，△ABC为等边三角形，边长为2，DE∥BC，△BCD的面积是△ABC的面积的，求EC的长.【答案与解析】一、选择题1．【答案】 B.【解析】如图，∵l1∥l2∥l3，∴，∴选项A、C、D均正确，故选B．2．【答案】 D.3．【答案】 C.【解析】∵DE∥BC，∴EC BDAC AB=,又∵，∴59BDAB=,即=59.4．【答案】D.【解析】∵DE∥AC，∴DE BDAC AB=，又∵AB=7cm，AC=5cm，AD=3cm，∴BD=4，即DE=207.5．【答案】C.【解析】提示：∵ DE∥BC，DF∥AC，∴DE=CF, DF=CE.6.【答案】B.【解析】作GM∥CD交AB于点M,∵E是AG中点，∴MG=2DE,又∵G是BC中点，∴CD=2MG=4DE ∴EC=3DG,即EC:DE=3:1.二、填空题7.【答案】0.8.8.【答案】4:3.【解析】∵DE∥BC, BF:EF=4:3，∴BF BC AC EF DE AE==9.【答案】6cm.【解析】∵点G是重心，∴AG:GD=2:1，又∵GD=2，∴AG=4，即AD=6cm.10.【答案】3:2.【解析】∵25AP BPAM BN==，∴23AP ABPM MN==.11.【答案】9.【解析】∵DE∥FG∥BC，∴=，而AD：DF：FB=3：2：1，∴=，∴=，∴EC=9．12.【答案】7.【解析】作DM∥AB,交EF,BC于点M,N,则EM=AD=BN=5，NC=3，又∵AD∥EF∥BC, 且AE=2EB,∴23DM MFDN NC==,∴MF=2，即EF=5+2=7.三、解答题13. 【解析】解：∵AB∥CD∥EF，∴OA OB AC BD=,又∵OA=14，AC=16，BD=12，∴OB=212.同理AC BDCE DF=,CE=8，∴DF=6.14.【解析】证明：∵EG∥CD，∴=，且，∴=，∴=，即=，∵AB=AC，∴AE=AF．15.【解析】解：作DM,AN垂直BC,垂足为点M,N，即DM∥AN,∵△BCD的面积是△ABC 的面积的，即14CDSS=△B△ABC=1212BC DMBC AN⋅⋅⋅,∴14DMAN=∵DM∥AN,∴DM BDAN BA=,∴BD=12.又∵AB=AC,DE∥BC,∴BD=EC=12.11 / 11。

19.3 平行线分三角形两边成比例
名师导学
典例分析
例1已知：如图19－3－4,AB//CD,∠EFB=∠ABC,AB=2,CD=4,则EF的长是多少?
思路分析：尽管题目中给出了AB//CD的条件,但不能直接运用相关的定理,因为它们分布在不同的三角形中,因而自然联想到在它们的中间作一条和它们都平行的辅助线,类似于桥梁的作用,这样便可解决问题.
解：过点E作EM//AB,.·.∠ABC=∠EMF,由已知∠ABC=∠EFB,∴∠EMF=∠EFM,∴EF=EM.∵AB//CD,∴
,∴.∵,∴,,
则.
例2如图19－3－5所示,△ABC中,D为BC的中点,延长AD至E,延长AB交CE于点P,若AD=2DE,试说明AP与AB 之间的数量关系.
思路分析:过点B作BK∥PC,交AE于点K,则可得.又BD=DC,∴DK=DE,再由AD=2DE,∴AE：AK=3,从而
进一步得出结论.另外还可以作以下的平行线,同样可得出结论,如：过D点作DG∥PC交即于点G,还可取CP的中点M,联结DM,进一步得出结论,这里只对第一种作辅助线的方法进行详细解答.
解：AP=3AB.
理由：过点B作BK∥PC,交AE于点K,∴AE：AK=AP：AB,由已知BD=DC,
∴DK：DE.又∵AD=2DE,∴AE：AK=3,∴AP：AB=3,即AP=3AB.
规律总结
善于总结★触类旁通
1 方法点拨：题目中涉及三角形中的平行线段,因此应考虑到利用“平行线分线段成比例”定理来求解.
2 方法点拨：利用平行线分线段成比例定理解题时,应注意利用特殊点,如中点、垂足等.本例中较多的辅助线作法是利用D为BC中点而作平行线,这也是作辅助线常用到的规律.。

北京版数学九年级上册《18.3 平行线分三角形两边成比例》教学设计一. 教材分析《18.3 平行线分三角形两边成比例》这一节主要讲述了利用平行线分三角形两边成比例的性质解决几何问题。

通过这一节的学习，学生能够掌握平行线分三角形两边成比例的定理，并能够运用该定理解决相关的几何问题。

二. 学情分析学生在学习这一节之前，已经学习了平行线的性质，三角形的相关知识，具备一定的几何知识基础。

但学生在解决实际几何问题时，还不能灵活运用所学知识。

因此，在教学过程中，教师需要引导学生将所学知识运用到实际问题中，提高学生的几何解决问题的能力。

三. 教学目标1.知识与技能：学生能够理解并掌握平行线分三角形两边成比例的定理，并能够运用该定理解决相关的几何问题。

2.过程与方法：通过观察、操作、猜想、验证等过程，培养学生的几何思维能力。

3.情感态度与价值观：学生能够积极参与课堂活动，提高对几何学科的兴趣。

四. 教学重难点1.重点：学生能够理解并掌握平行线分三角形两边成比例的定理。

2.难点：学生能够灵活运用平行线分三角形两边成比例的定理解决实际问题。

五. 教学方法1.情境教学法：通过设置实际问题情境，引导学生观察、操作、猜想、验证，激发学生的学习兴趣。

2.互助合作学习法：学生分组讨论，共同解决问题，培养学生的团队协作能力。

3.启发式教学法：教师引导学生思考，激发学生的思维能力。

六. 教学准备1.教师准备相关几何问题情境，制作PPT。

2.学生准备笔记本、文具等学习用品。

七. 教学过程1.导入（5分钟）教师通过设置一个实际几何问题情境，引导学生观察、操作，让学生感受到平行线分三角形两边成比例的性质。

2.呈现（10分钟）教师通过PPT呈现平行线分三角形两边成比例的定理，并解释定理的含义。

同时，教师可以举例说明该定理在解决实际几何问题中的应用。

3.操练（10分钟）教师引导学生分组讨论，共同解决一些与平行线分三角形两边成比例相关的几何问题。

ED CBA平行线分三角形两边成比例【学习目标】1．掌握平行线分三角形两边成比例的性质。

2．会对照图形写出正确的比例式。

3．会利用性质解决相关的计算和证明。

【学习重难点】会利用性质解决相关的计算和证明。

【学习过程】一、平行线分三角形两边成比例的性质：平行于三角形一边的直线截其他两边，所得的对应线段成比例。

（1）性质表示（如图）：//DE BC∴AD AEDB EC=∴ ∴ ∴（2）巧计性质，如右图，性质可以写成：=上上下下，=上上下下，=上上下下 ==上下全上下全注意：性质中所涉及的线段不包括DE BC 和 二、随堂练习1．如图1，若//DE BC ，则A D A E D BD B A C A B=== ， ， 。

2．如图1，⊿ABC 中，//,:2:3,:DE BC AD DB AE AC ==则 。

3．在⊿ABC 中，//DE BC ，且DE 交AB 于D ，交AC 于E ，则下列式子不能成立的是（ ） A ．AD AE DB EC = B ．AD AC AB AE = C ．AC EC AB DB = D ．AD DEDB BC =全全下下上上E DC BA图1EDCBAHAEBDC图5F4．如图2，⊿ABC 中，//DE BC ，若AE ：EC=3：5，求： （1）AD ：DB （2）AD ：AB （3）AB ：DB5．如图3，⊿ABC 中，EF//CD ，DE//BC ，求证：AF ADFD DB =三、课堂探究案：1．如图4，RT ⊿ABC 中，90,,12,C DE AC E AE ∠=⊥=于13,15,AD CE AB ===则 。

2．如图5，DE 是⊿ABC 的中位线，F 是DE 中点，BF 的延长线交AC 于H ，求：AH ：AE3．如图6，⊿ABC 中，//,//DE BC DF BA ，则下列各式中正确的是（ ） A ．AE ED EB DC = B ．DF DCAB BC= 图2A EBDC图3FCDBEA图6FED CBA图4EBDCC ．AE AF AB AC = D ．BD FCDC FA=【达标检测】1．如图，在⊿HPQ 中，若//,,MN PQ b a c a ≠≠，那么满足关系式bcx a=的图形是（ ）2．如图，在⊿ABC 中，AD 评分BAC ∠求证：BD ABDC AC =3．如图，在⊿ABC 中，AB=AC ，过AB 延长线上一动点D 作直线DE 交BC 于F ，交AC 于E ，求证：DF ：FE=BD ：CE4．如图，D 是⊿ABC 中BC 上一点，BD ：DC=2：1，E 是AD 中点，联结BE 并延长交AC 于点F 。

18.3平行线分三角形两边成比例考试总分：120分 考试时间：120分钟学校： 班级：姓名： 考号：、选择题（共10小题，每小题3分，共30分） 1.如图，丨'，两条直线与这三条平行线分别交于点 DE.的值为（）D 卜4.在梯形•'；'；'：；；中，止 m ：, •圧二® 川=门，两腰延长线交于点 二 过I'作.的平行线，交，■、：:延长线于、；：等于（）•、：、 和、、：.已知2.如图，在匕：H 中,•、 分别是.、.上的点，且二U ,若= ^：,贝yA. C.D.3.如图，某学生利用标杆测量一棵大树的高度，如果标杆■'?."= '，：•,「•'.= ' ：：丫，那么树 川：的高度是（）的高为’•■，并测得B. Gm D.0,125mAB 3A.-A.2abC. D.5. 如图，止mm：直线,与这三条平行线分别交于点•，: , ■和点■,,,二「 「则的值为（）BC 36.如图,f 、m 「、，直线、•与这三条平行线分别交于点:•若■■■>=f •：,.：「=」，贝y :的长为（）7.梯形中，对角线■■- '相交于点「，过-点的直线分别交上、下底于 、，则在图中与■-彳的比值相等的线段比有（）A.-个B.个C.个D.个9.如图，丨,'■- 交于点，则下列比例中成立的是（AB DE A —=— BC EFAB AD C — AC CF10.在 A ABC 中，冲DBD = 1:1,川1:2 , HE 与CD 交于点 P ,则 BP 屮E =()C. I'D.ID.，且：□=「；•，B. IC.D. AB ACD TIA.:A. ID £ CA. ： I DEE、填空题（共10小题，每小题3分，共30分）12. ____________________________________________________________ 如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的 三个点爪H 、匚都在横格线上•若线段 AU = 4cm ，则线段必=_________________________________________________________________________ cm .13.已知：如图,DE//RC , AE = 5, _________ = = 8，则 EC =14.如图，在梯形-n 中，出y •，一W分别交「， \ '于点、：、B. IC.D.A. JE沖甘 115.如图，直线 Wm.：C ，如果，：，：I 丨 ，•，那么线段’的长是CG ，； AG AB，旋二 -------- ，而BE CF 216. 如图，直线，另两条直线分别交=「」：=：,「二:，则: ① 占C:冲日= _________ ; ② 片甘:冲匚= _________ ; ③ BS DE = __________ ; ④ 耐貯= ______________ .17.在—汎中，点 乙 分别在边 厶 •的延长线上，且''」：；： =DE = 6= ______________________ .18. 如图，在中，H J J ；匕，心匕肚二 I ：；;, .：d ,求FC =AD 219.如图，\ 分别是―轧的边• 、•上的点, ，若. ，则AE无= ---------3 ■I,, 于点■,,，且、解答题（共6小题，每小题10分，共60分）EP21. 如图，在—中，，= 影丁，J：.连接.交•：于点，求，的值.22.如图1 二：■“ 二”'；；，那么二二、h •、：有什么关系?如图，辿：iw 肚，工; -■■■■■■，那么「与•有什么关系？23.如图二:U中，•在朋上，在’•上，.•与■交于点，；：：「=「；，；「= ,：.：，求BF AE:，.24.已知：如图于：, 为：’中点,-1 交.于:，小二，…'■', ；■：：：= »=：，求占*的长.yjjrj 貝童25・已知「中，•、分别为.、.上的点，且…二」交…于，连，并延1 A0•当• 时，求.的值；•当「二’时，求证：，•■二着(3)当叫=____________ 时，。

北京课改版数学九年级上册18.3《平行线分三角形两边成比例》教学设计1一. 教材分析《平行线分三角形两边成比例》是北京课改版数学九年级上册第18章第3节的内容。

本节课主要讲述了利用平行线分三角形两边成比例的性质解决几何问题的方法。

通过本节课的学习，学生能够掌握平行线分三角形两边成比例的定理，并能够运用该定理解决相关的几何问题。

二. 学情分析学生在学习本节课之前，已经掌握了相似三角形的性质、平行线的性质等基础知识。

但部分学生在解决实际几何问题时，仍存在运用不当的情况。

因此，在教学过程中，教师需要关注学生的学习情况，引导学生将理论知识运用到实际问题中。

三. 教学目标1.知识与技能：学生能够掌握平行线分三角形两边成比例的性质，并能够运用该性质解决相关的几何问题。

2.过程与方法：通过观察、操作、思考、交流等过程，培养学生解决问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队合作意识。

四. 教学重难点1.重点：平行线分三角形两边成比例的性质。

2.难点：如何运用平行线分三角形两边成比例的性质解决实际问题。

五. 教学方法1.情境教学法：通过设置实际问题，引导学生运用所学知识解决问题。

2.合作学习法：分组讨论，培养学生团队合作意识。

3.引导发现法：教师引导学生发现平行线分三角形两边成比例的性质，培养学生的探究能力。

六. 教学准备1.教具：多媒体课件、几何画板、黑板等。

2.学具：学生用书、练习题、彩笔等。

七. 教学过程1.导入（5分钟）教师通过展示一个实际问题，引导学生思考如何解决。

例如：在三角形ABC中，AB//CD，AE=CE，求证：AB/AC=BE/ED。

2.呈现（10分钟）教师利用几何画板展示平行线分三角形两边成比例的定理，引导学生观察、思考。

同时，教师讲解定理的证明过程。

3.操练（10分钟）教师给出几个练习题，让学生独立完成。

题目要求运用平行线分三角形两边成比例的性质解决问题。

教师巡视课堂，解答学生疑问。

19.3平行线分三角形两边成比例（一）平行线分三角形两边成比例***********************************************************************利用几何画板探究上述结论（利用几何画板进行探究）^教学冃^标 *************************************1. 掌握平行线分三角形两边成比例定理 （A 字形）2. 结合图形，能对定理中“对应”线段准确的认识3. 通过应用定理，提高识图能力和逻辑推理能力 ******************************************************************** 教学重点 *************************************准确找出对应线段********************************** 板书设计平行线分三角形两边成比例 1.平行线分三角形两边成比例定理*************************************图形变式 例2：********************************** 教学内■^容*************************************一、复习 填空：在厶ABC 中 •/ D 是 AB 中点 DE // BC AD BDAE AC 叙述定理 经过三角形一边中点且与另一边平行和直线必分第三边 二、新课 1.通过刚才的复习我们知道: AD 思考：如果把 DE 平行向上移动, 如果把DE 平行向上移动,AB 2 AD AB AD AB AE 1 AC 2 1 ，那么 3 1，那么 4些呢? AC 览呢? AC思考：如果DE 平行移动，使 AD m二 一(m 、AB nn 没有公因数），那么jAE呢?AC2.得出结论，若DE // BC ,、，亠AD AE 左上 总有忑二怎（左全-右全一右上）教学难点注：等式左右两边交换位置亦可。