连续信号的拉普拉斯变换分析.
- 格式:ppt
- 大小:793.50 KB
- 文档页数:8






一、介绍拉普拉斯变换是一种用来分析和处理连续时间信号的数学工具。
它在控制理论、信号处理和电路分析等领域有着广泛的应用。
本文将围绕着表达式x(-t+3)的拉普拉斯变换展开讨论,探讨其在实际问题中的应用。
二、x(-t+3)的拉普拉斯变换拉普拉斯变换是一种用于将连续时间信号转换为复频域的数学工具。
对于表达式x(-t+3),它的拉普拉斯变换可以通过以下步骤来求解。
1. 根据拉普拉斯变换的定义,我们需要将表达式x(-t+3)乘以e^(-st),其中s为复变量。
这样得到的新表达式为x(t)e^(-3s)e^(-st)。
2. 我们需要对新表达式进行积分运算。
将x(t)e^(-3s)e^(-st)关于t进行积分,得到积分表达式∫x(t)e^(-3s)e^(-st)dt。
3. 对积分表达式进行求解,得到x(-t+3)的拉普拉斯变换。
三、应用举例x(-t+3)的拉普拉斯变换在实际问题中有着重要的应用。
以下举例说明其在控制理论和信号处理中的应用。
1. 控制理论在控制系统中,经常需要对输入信号进行变换和处理。
对于一个以时间t为自变量的输入信号x(t),我们希望将其延迟3个时间单位后输入系统中。
这时就需要用到x(-t+3)的拉普拉斯变换。
通过对输入信号进行拉普拉斯变换,可以方便地对系统的动态特性进行分析和控制。
2. 信号处理在信号处理中,经常需要对信号进行时移和频率变换。
对于表达式x(-t+3),其拉普拉斯变换可以帮助我们分析信号在频域中的特性。
可以通过变换后的频域表达式来设计滤波器、降噪和提取信号特征等。
四、结论本文围绕着表达式x(-t+3)的拉普拉斯变换展开讨论,介绍了其求解步骤和在控制理论和信号处理中的应用。
拉普拉斯变换作为一种重要的数学工具,对于分析和处理连续时间信号有着重要的意义,希望本文的内容对读者有所启发和帮助。
一、引言拉普拉斯变换是一种在工程和科学领域中被广泛应用的数学工具,它能够将时域中的函数变换到复频域中,为我们探索和分析系统的动态特性提供了有力的工具。




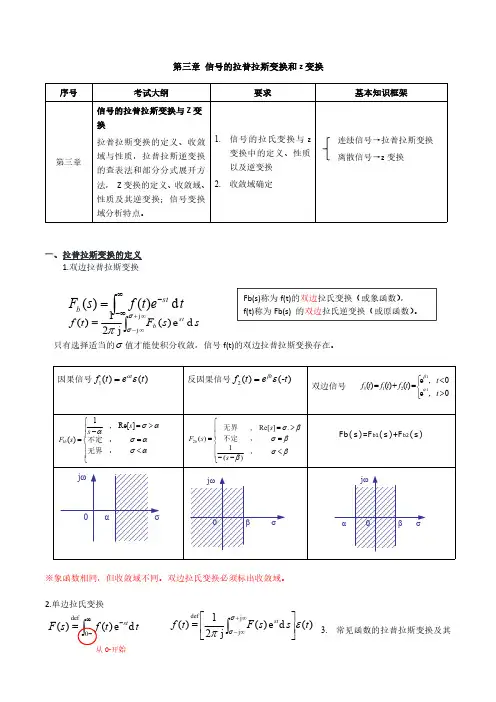
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛,信号f(t)的双边拉普拉斯变换存在。
※象函数相同,但收敛域不同。
双边拉氏变换必须标出收敛域。
2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换(或象函数),f(t)称为Fb(s)的双边拉氏逆变换(或原函数)。
从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明:[]⎰∞--=de)()(tatfatf L st,则令atτ=时移特性与尺度变换相结合复频移(s域平移)特性时域的微分特性(微分定理)若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明:()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广:()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0,且有实数a>0,则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2:?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法:(1)查表(2)利用性质(3)部分分式展开-----结合∴......,,321为不同的实数根,n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式,可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n (假分式),可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。
信号与系统的拉普拉斯变换是一种数学工具,用于分析线性时不变系统的行为。
它通过将信号或系统表示为复指数的线性组合,将时间域的信号或系统转换为频域表示。
在频域中,系统的性质可以更容易地理解和分析。
拉普拉斯变换具有收敛域的性质,这是其定义的一部分。
收敛域是复平面上使得拉普拉斯变换存在的点。
此外,拉普拉斯变换具有一些重要的性质,包括线性性质、时移性质、频移性质、微分性质和积分性质等。
这些性质在分析系统时非常有用。
此外,拉普拉斯变换在分析线性时不变系统的稳定性方面具有重要作用。
通过分析系统的极点和零点分布,可以确定系统的稳定性。
极点和零点是系统函数的根,它们在复平面上的位置决定了系统的动态行为。
总之,信号与系统的拉普拉斯变换是理解和分析线性时不变系统的重要工具,它可以转换时间域的信号或系统到频域表示,提供了一种方便的方式来理解和分析系统的动态行为和稳定性。
信号的拉普拉斯变换一、引言信号处理是现代通信系统、控制系统以及多种科学工程领域中的一个重要基础理论。
信号的拉普拉斯变换是信号处理中的一种常用数学工具,用于对信号进行频域分析和系统建模。
本文将从信号的概念、拉普拉斯变换的定义与性质以及拉普拉斯变换在信号处理中的应用等方面进行全面、详细地探讨。
二、信号的概念信号在工程领域中广泛存在,可以理解为随时间变化的物理量或信息载体。
根据信号的不同特征,可以将信号分为连续信号和离散信号两类。
连续信号在时间上是连续变化的,通常用连续函数表示;离散信号则是在时间上离散变化的,通常用序列表示。
三、拉普拉斯变换的定义与性质3.1 定义拉普拉斯变换是一种用于将时间域中的函数转换为频域中的函数的数学工具。
给定一个连续时间函数f(t),其拉普拉斯变换F(s)定义为:F(s) = ∫[0,∞) f(t)e^(-st)dt其中,s是复变量, e^(-st) 是指数衰减项,表示时间域函数在s平面上的对应点。
3.2 常见拉普拉斯变换常见的拉普拉斯变换对照表如下:时间域函数 f(t) 拉普拉斯变换 F(s)δ(t) 断定脉冲 1u(t) 单位阶跃函数1/se^(-at) 指数衰减函数1/(s+a)时间域函数 f(t) 拉普拉斯变换 F(s)t^n 多项式函数n!/(s^(n+1))3.3 拉普拉斯变换的性质拉普拉斯变换具有许多重要性质,这些性质在信号处理中具有广泛的应用。
以下是一些常见的拉普拉斯变换性质: 1. 线性性质:拉普拉斯变换是线性的,即常数倍和加法都可以在拉普拉斯域中进行。
2. 移位性质:拉普拉斯变换中的移位可以用于推导信号的时移和频移。
3. 初值定理和终值定理:初值定理和终值定理是拉普拉斯变换的重要性质,可以用于计算信号在t=0和t=∞时的值。
4. 差分性质:拉普拉斯变换在微分和积分方面也具有重要的性质,在求解微分方程和积分方程中有广泛应用。
四、拉普拉斯变换在信号处理中的应用拉普拉斯变换在信号处理中具有广泛的应用,下面列举了一些常见的应用:4.1 线性时不变系统的分析拉普拉斯变换可以用于描述线性时不变系统的传递特性。
信号与系统拉普拉斯变换及res[s]的应用一、引言在信号与系统的研究中,拉普拉斯变换是一种重要的数学工具,可以用来处理复杂的连续时间信号和系统。
本文将重点介绍拉普拉斯变换以及其中的一个重要概念res[s],并探讨其在信号与系统中的应用。
二、拉普拉斯变换概述1. 拉普拉斯变换的定义拉普拉斯变换是傅立叶变换的推广,用于将时域中的连续信号转换到复频域中。
对于一个连续时间信号f(t),其拉普拉斯变换F(s)定义如下:F(s) = L{f(t)} = ∫[0,∞] e^(-st) f(t) dt其中,s为复数变量,t为时间变量,e^(-st)为指数衰减函数。
2. 拉普拉斯变换的性质拉普拉斯变换具有线性性、时移性、频移性、尺度变换等性质,使得它能方便地处理复杂的信号和系统问题。
三、res[s]的概念1. res[s]的定义res[s]是拉普拉斯变换中的一个重要概念,它描述了信号或系统的稳定性特性。
res[s]的定义如下:若f(t)的拉普拉斯变换F(s)满足lim(s→∞) sF(s) = 0,称F(s)具有res[s]。
2. res[s]的性质具有res[s]的信号或系统在时域中具有稳定性,也就是说其响应不会无限增长或衰减。
这对于工程问题和控制系统设计至关重要。
四、res[s]的应用1. 稳定性分析利用res[s]的概念可以进行信号和系统的稳定性分析。
通过求取信号或系统的拉普拉斯变换,并判断其res[s],可以确定其在时域中的稳定性特性。
2. 控制系统设计在控制系统设计中,需要保证系统的稳定性,否则会导致系统不可控或不稳定。
利用res[s]的概念可以帮助工程师评估控制系统的稳定性,并进行相应的优化和修正。
3. 信号处理在信号处理领域,res[s]也有着重要的应用。
稳定的信号处理系统能够更准确地提取、分析和处理信号,因此res[s]的概念在信号处理算法的设计和分析中起着关键作用。
五、结论拉普拉斯变换及其中的res[s]概念在信号与系统领域具有重要的理论和实际意义。