下载文档原格式
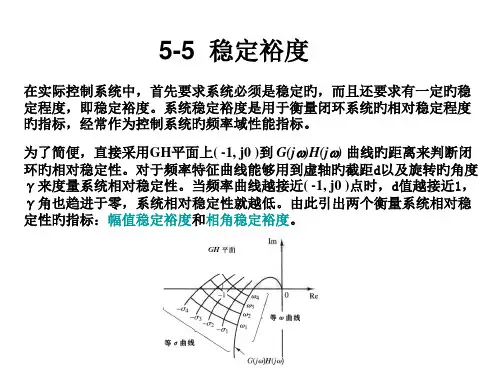
5.8 稳定裕度5.8 稳定裕度对一个最小相角系统而言，G(j w ) 曲线包围(-1, j0)点系统不稳定，不包围(-1, j0)点系统稳定，恰好经过(-1, j0) 点系统临界稳定。
G(j w ) 曲线越靠近(-1, j0)点，系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
相角裕度和幅值裕度是系统开环频域指标，它们与系统的动态性能密切相关。
因此，可以用G(j w ) 曲线与(-1, j0)点的接近程度来表示系统的相对稳定性。
通常，这种接近程度以相角裕度和幅值裕度来表示。
的几何意义h ,γcω截止频率γ相角裕度()c =︒+∠180j G γw ()c =j 1G ωg ω相角交界频率h幅值裕度()g =1j h G w ()g ∠=−︒j 180G ω的物理意义h ,γ系统在方面的稳定储备量γh 幅值相角一般要求︒>40γ2>h相角裕度的物理意义：系统在相角上距离临界稳定还具有的储备量幅值裕度的物理意义：系统在增益上距离临界稳定还具有的储备量一般要求︒>40γ2>h)(180c j G w γ∠+︒=解法I ：由幅相曲线求。
h ,γ例1)10)(2(100)110)(12(5)(++=++=s s s s s s s G ，求。
h ,γ(1)令()c =j 1G ω2222102100++=c c c w w w 242[104400]10000c c c w w w ++=9.2=c w 解得)9.2(180ϕ+︒=109.2arctan 29.2arctan 90180−−︒−︒=︒=︒−︒−︒=5.181.164.55905.8 稳定裕度(2) 令︒−=180)(g w ϕ10arctan 2arctan 90g g w w −−︒−=可得︒=+9010arctan 2arctan g g w w 47.4=g w )(1g j G h w =4.24167.01==例1)10)(2(100)110)(12(5)(++=++=s s s s s s s G ，求。
控制系统稳定裕度设计控制系统的稳定性是系统工程中至关重要的一环。
稳定裕度是控制系统在面对外部扰动时能保持稳定的能力。
本文将讨论控制系统稳定裕度的概念、影响因素以及设计原则。
一、稳定裕度的概念稳定裕度是指控制系统在满足性能要求的同时，对于内外部扰动能够保持稳定的能力。
通常用裕度指标来描述系统的稳定性，例如相位裕度和增益裕度。
相位裕度是指系统的相位与临界相位的差值，增益裕度是指系统增益与临界增益的差值。
二、影响因素1. 系统动态特性：系统的动态特性直接影响稳定裕度。
例如，系统的阻尼比、谐振频率以及过冲量等参数都会对稳定裕度产生影响。
2. 控制器设计参数：控制器的设计参数会直接影响稳定裕度。
例如，比例系数和积分时间常数的选择都会对稳定裕度产生影响。
3. 系统外部扰动：外部扰动的大小和频率对系统的稳定性有直接影响。
稳定裕度设计需要考虑外部扰动的影响。
三、稳定裕度设计原则1. 设定合适的相位裕度：相位裕度是决定系统稳定性的重要指标。
通常，相位裕度应大于一定阈值，以确保系统不会产生不稳定的振荡。
2. 提高增益裕度：增益裕度是指系统增益与临界增益的差值，也是保证系统稳定性的关键因素。
增益裕度的提高可以通过合适的控制器设计参数以及系统结构的良好调整来实现。
3. 引入补偿网络：通过引入补偿网络可以改善系统的稳定裕度。
常用的补偿网络包括PID控制器、滤波器等。
4. 考虑外部扰动：稳定裕度设计需要充分考虑外部扰动对系统稳定性的影响。
可以采用滤波器、增加机械结构等手段来减小外部扰动的影响。
四、结论控制系统稳定裕度的设计是确保系统稳定性的关键步骤。
通过正确选择相位裕度和增益裕度，优化控制器设计参数以及考虑外部扰动的影响，可以提高系统的稳定性。
这将有助于系统的性能优化，提高工程的可靠性和稳定性。
在控制系统中，稳定裕度的合理设计对于保证系统稳定性和性能具有重要作用。
我们应该深入理解稳定裕度的概念、影响因素以及设计原则，并根据具体系统的特点和需求进行相应的设计和优化。
飞机稳定裕度计算
飞机的稳定裕度通常以飞机的焦点到重心的距离占机翼平均空气动力弦长的百分比来表示，且焦点位于重心之后为正，反之为负。
早期，战斗机的纵向稳定裕度为正5%左右，运输机的纵向稳定裕度一般为正5%-10%。
飞机的纵向稳定性条件也适用于羽毛球、纸飞机、毽子等体育、娱乐用品。
除纵向稳定性外，飞机还有横向稳定性和方向稳定性问题，三者大体类似，不再逐一展开。
飞机的稳定裕度是一个重要的参数，它可以帮助设计者评估飞机的稳定性，并优化飞机的设计。
稳定性分析与稳定裕度稳定性是指系统在受到内外部扰动时能否回到平衡状态的能力。
稳定裕度则是指系统能够容忍的扰动大小。
在工程领域中，稳定性分析和稳定裕度的研究对于保障系统的安全可靠性至关重要。
本文将介绍稳定性分析与稳定裕度的概念、计算方法以及其在不同领域的应用。
一、稳定性分析的概念稳定性分析是一种评估系统稳定性的方法。
它可以通过分析系统的特性和参数来判断系统在遭受外界扰动时是否能够保持平衡。
在稳定性分析中，常用的方法包括等效线性化、Bifurcation分析、Lyapunov稳定性分析等。
等效线性化是一种常见的稳定性分析方法。
它通过将非线性系统在某一特定工作点附近进行线性化处理，得到等效线性系统，并通过研究其特征根来判断系统的稳定性。
Bifurcation分析则是研究系统在参数变化过程中平衡点的分岔情况，以此来判断系统是否存在稳定性转变。
而Lyapunov稳定性分析则是利用Lyapunov函数的性质来评估系统的稳定性。
二、稳定裕度的计算稳定裕度是评估系统稳定性的指标之一。
它是指系统在遭受一定范围内的扰动时能够保持稳定的能力。
稳定裕度的计算通常涉及到系统的摄动响应和性能指标的定义。
摄动响应是指系统在受到扰动时的响应情况。
常见的稳定裕度指标包括幅值裕度和相位裕度。
幅值裕度是指系统在受到特定幅值的扰动时，输出信号的幅值与输入信号幅值之间的差值。
相位裕度则是指系统在受到特定相位的扰动时，输出信号相位与输入信号相位之间的差值。
稳定裕度的计算与系统的数学模型和特性密切相关。
在实际工程中，可以通过仿真实验或实际测试来获取系统的摄动响应，从而计算稳定裕度。
此外，还可以通过建立数学模型，利用控制理论和信号处理方法来计算稳定裕度。
三、稳定性分析与稳定裕度的应用稳定性分析与稳定裕度的研究在众多领域中都有广泛的应用。
以下是几个典型的应用案例：1.电力系统稳定性分析：电力系统中存在较大的复杂性和不确定性，稳定性分析可以帮助评估系统的动态响应和抗干扰能力，为电力系统的设计和运行提供指导。
5.5 稳定裕度
5.5.1 稳定裕度的定义
控制系统稳定与否是绝对稳定性的概念。
而对一个稳定的系统而言，还有一个稳定的程度，即相对稳定性的概念。
相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不仅要求它必须是绝对稳定的，而且还应保证系统具有一定的稳定程度。
只有这样，才能不致因系统参数变化而导致系统性能变差甚至不稳定。
对于一个最小相角系统而言，()G j ω曲线越靠近（1,0j -）点，系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
因此，可用)(ωj G 曲线对（0,1j -）点的接近程度来表示系统的相对稳定性。
通常，这种接近程度是以相角裕度和幅值裕度来表示的。
相角裕度和幅值裕度是系统开环频率指标，它与闭环系统的动态性能密切相关。
1 相角裕度
相角裕度是指幅相频率特性)(ωj G 的幅值1)()(==ωωj G A 时的向量与负实轴的夹角，常用希腊字母γ表示。
图5-46 相角裕度和幅值裕度的定义 图5-47稳定裕度在Bode 图上的表示
在G 平面上画出以原点为圆心的单位圆，见图5-46。
)(ωj G 曲线与单位圆相交，交点处的频率c ω称为截止频率，此时有1)(=c A ω。
按相角裕度的定义
)
(180
)180()(c c ωϕωϕγ+=--=
（5-59）
由于01lg 20)(lg 20)(===c c A L ωω，故在伯德图中，相角余度表现为
dB
L 0)(=ω处的相角)(c ωϕ与 180-水平线之间的角度差，如图5-46所示。
上述
两图中的γ均为正值。
2 幅值裕度
)
(ωj G 曲线与负实轴交点处的频率g ω称为相角交界频率，此时幅相特性曲
线的幅值为)(g A ω，如图5-45所示。
幅值裕度是指（0,1j -）点的幅值1与)(g A ω之比，常用h 表示，即
)
(1g A h ω=
（5-60）
在对数坐标图上
20lg 20lg ()()g g h A L ωω=-=-
（5-61）
即h 的分贝值等于)(g L ω与dB 0之间的距离（dB 0下为正）。
相角裕度的物理意义在于：稳定系统在截止频率c ω处若相角再迟后一个γ角度，则系统处于临界状态；若相角迟后大于γ，系统将变成不稳定。
幅值裕度的物理意义在于：稳定系统的开环增益再增大h 倍，则g ωω=处的幅值)(g A ω等于1，曲线正好通过（0,1j -）点，系统处于临界稳定状态；若开环增益增大h 倍以上，系统将变成不稳定。
对于最小相角系统，要使系统稳定，要求相角裕度0>γ，幅值裕度1>h 。
为保证系统具有一定的相对稳定性，稳定裕度不能太小。
在工程设计中，一般取
60~30=γ，2≥h 对应20lg 6h dB ≥。
5.5.2 稳定裕度的计算
根据式（5-59）,要计算相角裕度γ，首先要知道截止频率c ω。
求c ω较方便的方法是先由)(s G 绘制)(ωL 曲线，由)(ωL 与dB 0线的交点确定c ω。
而求幅值裕度h 首先要知道相角交界频率g ω，对于阶数不太高的系统，直接解三角方程
180)(-=∠g j G ω是求g ω较方便的方法。
通常是将)(ωj G 写成虚部和实部，令虚部为零而解得g ω。
例5-12 某单位反馈系统的开环传递函数为
)
5)(1()(0
++=
s s s K s G
试求100=K 时系统的相角裕度和幅值裕度。
解 ⎩⎨
⎧==++=
1
5
)
151)(
1(5)(00υK K s s s K s G 绘制开环增益250==K K 时的)(ωL 曲线如图5-48所示。
当2=K 时
)20(2
1
2
11
)5
(
1
2
)(2
2
2
2
2
2
2
<<=≈
=++=
c c
c
c c c c c A ωωωωωωωω
所以 2=c ω
5
.198.157.54905
arctan
arctan 90180
)
(180
1=--=---=∠+=c
c c j G ωωωγ
又由 0)5arctan(arctan 90180)(180=---=∠+︒g g g j G ωωω 有 arctan arctan(90o g g ωω+=
等式两边取正切： ∞==⎥⎥⎥⎥
⎦
⎤
⎢⎢⎢⎢⎣
⎡-
+
90tan 5152
g g g ωωω
得 0512
=-g
ω，即 236
.25==
g ω。
dB
A h g
g g g 9.8793.22
1
)5
(
1)
(12
2
1==++=
=
∴
ωωωω
在实际工程设计中，只要绘出)(ωL 曲线，直接在图上读数即可，不需太多计算。
图5-48 2=K 时的)(ωL 曲线。
