下载文档原格式
固体颗粒的沉降分析
实验步骤
1.配制1000 mL1%阿拉伯树胶溶液：可在恒温水浴中加热使其溶解，温度不高于50℃。
2.往1000 mL量筒中加入阿拉伯树胶溶液，金属盘浸入溶液中，垂直悬挂。
打开扭力天平的制动旋钮。
旋转读数指针转盘，使平衡指针与零线重合，读数。
用刻度尺量金属盘到液面的距离。
关闭制动旋钮，将金属盘取出。
2.往量筒中加入15.0g碳酸钙粉末（称量在270），用搅拌棒上下均匀轻轻搅拌，搅拌时勿剧烈搅拌，以免产生气泡。
迅速将金属盘浸入量筒中，垂直悬挂，开始计时。
当金属盘位置稳定后，打开扭力天平的制动旋钮，不断旋转读数指针转盘，使平衡指针与零线重合，读数，并记下对应的时间。
从搅拌完毕到第一次读数，动作要迅速，时间越短越好，一般以15-20 s为宜。
每当金属盘上沉积的量增加约10 mg时记录读数和对应的时间，2min后每当金属盘上沉积的量增加约2 mg 时记录读数和对应的时间直至30 min。
关闭扭力天平的制动旋钮。
4.取下金属盘，将金属盘上的沉积物清洗下来。
继续轻轻搅拌，放入金属盘按前述方法重复测量一次。
5.实验完毕，关闭天平的制动旋钮，取出金属盘，倒掉量筒中的悬浊液，并洗净金属盘和量筒。
将金属盘挂在挂钩上。
注意：每次对金属盘进行操作时要关闭制动旋钮。
金属盘要轻拿轻放。
流态化基本原理【摘要】流态化技术是利用流动流体的作用，将固体颗粒群悬浮起来，从而使固体颗粒具有某些流体表观特征，利用这种流体与固体间的接触方式实现生产过程的操作。
自由沉降速度，又称终端速度。
指任一颗粒的沉降不因流体中存在其他颗粒而受到干扰时，在等速阶段里颗粒相对于流体的运动速度。
即加速阶段终了时颗粒相对于流体的速度。
关键词：流态化；固体；颗粒；沉降1流态化与自由沉降流态化一般指固体流态化，又称假液化，简称流化，它是利用流动流体的作用，将固体颗粒群悬浮起来，从而使固体颗粒具有某些流体表观特征，利用这种流体与固体间的接触方式实现生产过程的操作，称为流态化技术，属于粉体工程的研究范畴。
流态化技术是一种强化流体(气体或液体)与固体颗粒间相互作用的操作，如在直立的容器内间歇地或连续地加入颗粒状固体物料，控制流体以一定速度由底部通入，使其压力降等于或略大于单位截面上固体颗粒的重量，固体颗粒即呈悬浮状运动而不致被流体带走。
流态化技术在强化某些单元操作和反应过程以及开发新工艺方面，起着重要作用，广泛应用于化学、石油、冶金、原子能等工业的焙烧、干燥、吸附、气化、催化反应和催化裂化等许多过程中。
单个颗粒在流体中的沉降过程称为自由沉降。
若颗粒数量较多，相互间距离较近，则颗粒沉降时相互间会干扰，称为干扰沉降。
颗粒刚开始沉降时，速度u 为零，则曳力也为零，颗粒在净质量力（质量力与浮力之差）作用下沿质量力方向作加速运动，随着运动速度u的增加，曳力开始由零不断增大，直至与净质量力相等为止，这时，颗粒加速度减为零，速度u达到一恒定值，也是最大值，此后，颗粒等速下降，这一最终的运动速度称为沉降速度。
由此可见，单个颗粒在流体中的沉降过程分为两个阶段：加速段和等速段，对于小颗粒，加速段极短，通常可以忽略，于是，整个沉降过程都可认为是匀速沉降。
2流态化现象将一批固体颗粒堆放在多孔的分布板上形成床层，使流体自下而上通过床层。
由于流体的流动及其与颗粒表面的摩擦，造成流体通过床层的压力降。
化工原理中的沉降与过滤引言在化工工艺中，沉降和过滤是常用的固液分离方法。
沉降是指根据固液颗粒的重力作用，通过静置使固体颗粒沉降到底部，而将悬浮液体分离出来。
过滤则是通过利用滤介质的孔隙或表面，将悬浮液体中的固体颗粒留下，而使液体通过，从而达到分离固液的目的。
本文将从理论和实际应用两个方面，对化工原理中的沉降与过滤进行介绍。
沉降原理沉降是基于固体颗粒的重力作用，通过静置使固体颗粒沉降到底部，从而实现固液分离的过程。
沉降速度取决于固体颗粒与液体的密度差和粒径大小。
根据Stokes定律，沉降速度与颗粒直径的平方成正比，与液体的粘度成反比。
沉降速度可由下式计算：v = (2/9) * (ρp - ρl) * g * (d^2) / μ其中，v为沉降速度，ρp为颗粒的密度，ρl为液体的密度，g为重力加速度，d为颗粒的直径，μ为液体的动力粘度。
过滤原理过滤是通过滤介质的孔隙或表面，将悬浮液体中的固体颗粒留下，而使液体通过，从而实现固液分离的过程。
滤介质常用的有滤纸、滤筒、滤板等，其孔隙大小决定了能够透过的颗粒大小。
根据Darcy定律，过滤速度与滤介质的孔隙直径的平方成正比，与液体的粘度成反比。
过滤速度可由下式计算：Q = (π/4) * (d^2) * (ΔP/μ) * A其中，Q为过滤速度，d为滤介质的孔隙直径，ΔP为过滤压差，μ为液体的动力粘度，A为过滤面积。
实际应用沉降的应用沉降在化工过程中被广泛应用，常见的应用场景包括：1.污水处理：污水中悬浮的固体颗粒通过沉降实现固液分离，从而达到净化水质的目的。
2.矿石提取：矿石中的有用矿物颗粒通过沉降分离出来，然后进行后续的加工和提取。
3.食品加工：在食品饮料生产中，一些颗粒物质需要通过沉降分离，以获得纯净的液体产品。
4.生物工程：在细胞培养和发酵工艺中，需要将细胞或发酵产物与培养基进行分离。
沉降是一种常用的分离方法。
5.药物制剂：在药物合成和制剂工艺中，沉降用于分离和提取所需的纯净物质。
竭诚为您提供优质文档/双击可除颗粒自由沉降实验报告篇一：颗粒自由沉降实验颗粒自由沉淀实验一、实验目的1、过实验学习掌握颗粒自由沉淀的试验方法。
2、进一步了解和掌握自由沉淀的规律，根据实验结果绘制时间－沉淀率（t-e）、沉速－沉淀率（u-e）和ct/co~u 的关系曲线。
二、实验原理沉淀是指从液体中借重力作用去除固体颗粒的一种过程。
根据液体中固体物质的浓度和性质，可将沉淀过程分为自由沉淀、沉淀絮凝、成层沉淀和压缩沉淀等4类。
本实验是研究探讨污水中非絮凝性固体颗粒自由沉淀的规律。
实验用沉淀管进行。
设水深为h，在t时间内能沉到深度h颗粒的沉淀速度vh/t。
根据给定的时间to计算出颗粒的沉速uo。
凡是沉淀速度等于或大于u0的颗粒在t0时就可以全部(:颗粒自由沉降实验报告)去除。
设原水中悬浮物浓度为co则沉淀率＝(co-ct)／c0×100%在时间t时能沉到深度h颗粒的沉淀速度u:u=(h×10)／(t×60)(mm／s)式中：c0——原水中所含悬浮物浓度，mg/lc1————经t时间后，污水中残存的悬浮物浓度，mg/l;h——取样口高度cm;t——取样时间，min。
三、实验步骤1、做好悬浮固体测定的准备工作。
将中速定量滤纸选好，放入托盘，调烘箱至105±1℃，将托盘放入105℃的烘箱烘45min,取出后放入干燥器冷却30min，在1/10000天平上称重，以备过滤时用。
2、开沉淀管的阀门将软化淤泥和水注入沉淀管中曝气搅拌均匀。
3、时用100ml容量瓶取水样100ml(测得悬浮物浓度为c0)记下取样口高度，开动秒表。
开始记录沉淀时间。
4、时间为5、10、15、20、30、40、60min时，在同一取样口分别取100ml水样，测其悬浮物浓度为（ct）。
5、一次取样应先排出取样口中的积水，减少误差，在取样前和取样后必须测量沉淀管中液面至取样口的高度，计算时采用二者的平均值。
自由沉淀实验报告自由沉淀是一种常见的实验方法，用于研究固体颗粒在液体中的沉降速度及其与环境因素的关系。
通过该实验可以了解颗粒的密度、粒径等物理性质，并且还可以探究溶液浓度、温度、搅拌等因素对沉降速度的影响。
1. 实验目的本次实验的目的是通过观察和测量溶液中固体颗粒的沉降速度，探究不同因素对沉降速度的影响，以及分析颗粒的物理性质。
2. 实验材料与设备- 固体颗粒：选用具有一定大小和可见度的沉降颗粒，如砂子或小玻璃珠等；- 溶液：选用透明的液体作为溶液，如清水或食用盐水溶液等；- 容器：使用透明的容器，如玻璃烧杯或塑料瓶等；- 搅拌器：可选用玻璃棒或磁力搅拌子等。
3. 实验步骤a. 准备工作：清洗容器和搅拌器，确保无杂质；b. 加入溶液：按照实验要求，加入一定量的溶液到容器中；c. 加入颗粒：将一定数量的颗粒加入到溶液中；d. 开始计时：在开始观察颗粒沉降前，记录开始时间；e. 观察和记录：观察颗粒在溶液中的沉降情况，并记录不同时间点的沉降高度或沉降速度；f. 添加搅拌：根据实验需要，可以添加搅拌器进行搅拌，并观察搅拌对沉降速度的影响；g. 改变温度或浓度：根据实验要求，可以改变温度或浓度，并观察对沉降速度的影响；h. 结束实验并记录数据：当颗粒沉降到一定高度或实验时间结束后，停止观察并记录实验数据。
4. 实验结果与分析根据实验数据，可以制作颗粒的沉降曲线图，用沉降高度或沉降速度随时间的关系来表示。
通过观察沉降曲线，我们可以得出以下结论：a. 颗粒的沉降速度随时间的增加而减小，最终趋于稳定；b. 搅拌会影响颗粒的沉降速度，搅拌越强，沉降速度越快；c. 浓度对颗粒的沉降速度有一定影响，浓度越高，沉降速度越快；d. 温度对颗粒的沉降速度也有影响，温度越高，沉降速度越快。
5. 结论与讨论通过本次实验，我们得出了颗粒沉降速度与时间、搅拌、浓度和温度等因素之间的关系。
这些关系对于理解颗粒在液体中的运动行为和物理性质具有重要意义。
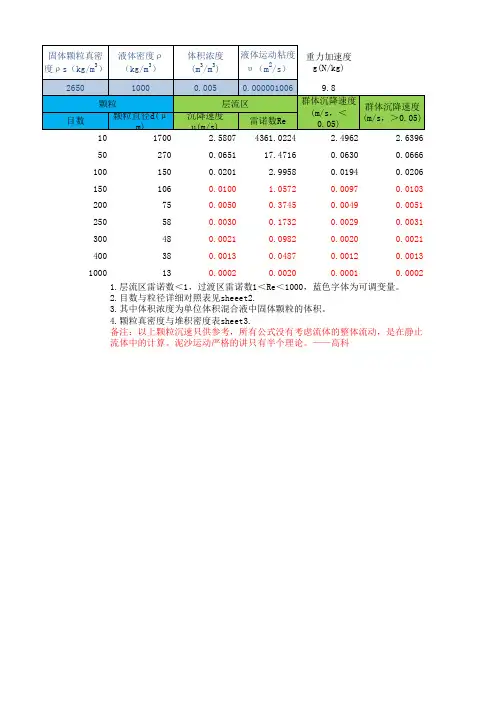
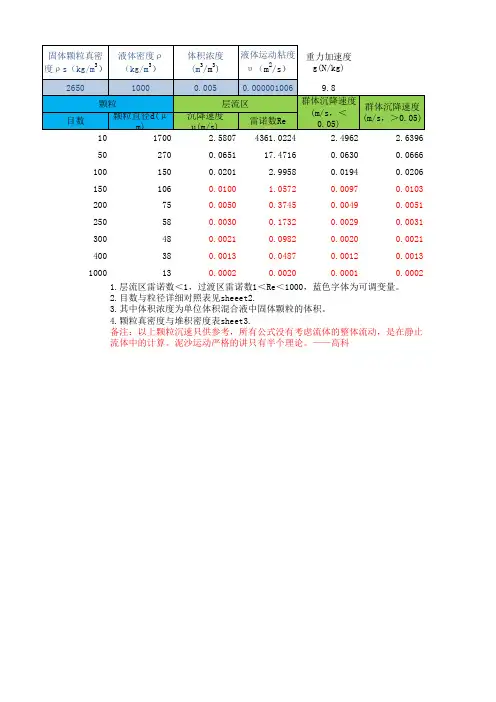
固体颗粒的群体沉降速度分析郑邦民1，夏军强2(1.武汉大学河流系，湖北武汉430072; 2.清华大学水利系，北京100084)摘要：从流体力学原理出发，数值模拟非均匀沙随机分布对流场的影响，推导出固体颗粒群体沉速的理论解。
该公式不仅量纲和谐，浓度变化不超过极限浓度值，能反映含沙量与非均匀沙级配变化对群体沉速的影响，而且可避免其它公式量纲不和谐，计算中出现负值或降得过快的缺点。
采用黄河实测资料对该公式进行了验证，计算结果与实测资料基本符合。
关键词：固体颗粒; 群体沉速; 干扰流核；极限浓度1 引言泥沙在静止的清水中等速下沉时的速度，称为泥沙的沉降速度。
在多沙河流的浑水中，泥沙颗粒的沉降特性比清水中与低含沙水流中复杂。
此时泥沙颗粒下沉相互干扰，部分颗粒或全部颗粒成群下沉，其下沉速度称为群体沉速［1,2］。
群体颗粒沉降特性的研究具有十分重要的意义，它在多沙河流的河床演变分析和泥沙数学模型计算中广泛应用。
单个颗粒的沉速与群体沉降可以相差10倍，故50年前有人说泥沙运动严格地讲只有一个半理论。
为此应进一步分析颗粒群体沉降规律，使其在实际应用中不致有太大的误差。
本文在研究流体力学粘性流中圆球绕流规律的基础上，得出固体颗粒群体沉速的理论解，它可反映泥沙浓度与组成对群体沉速的影响。
然后将该公式与现有的群体沉速公式进行比较，并用黄河实测资料进行验证。
2 理论前提Navier_Stokes方程是流体力学的基本控制方程，它是求解流体力学诸多问题中普遍应用的方程。
对不可压缩粘性流体，在有势外力作用下，可得Helmholtz 涡量方程(1)上式中为流速矢量：Δ为哈密顿算子(Hamilton Operator)；ν为流体的运动粘滞系数;t为时间。
一般情况下，三维流函数为向量，它与流速有如下关系。
而流速与涡量，亦呈旋度关系，即。
为了便于数值计算，它可写作一般曲线坐标系的张量形式：。
其中。
式中ui为逆变分量，Δj 为协变导数，为协变基向量，它不一定是正交基，也不一定为单位基。
对正交曲线坐标，则有其中u k为单位正交(局部)基上的物理分量；H k为Lami系数或标量因子，它反映微元弧长dd i与坐标微元dξi之间的比，即ds i=H(i)dξi。
根据上述关系，我们可以将涡量方程写作一般曲线坐标形式或正交曲线坐标形式，以便于数值计算。
它可以用来计算形体绕流等外部流动。
对于二维流或在柱坐标、球坐标下的球对称，轴对称流动，式(2)可以简化。
例如，在球坐标下有H1=1、H2=R、H3=Rsinθ，可得ds1=dR、ds2=dθ、ds3=Rsinθdλ。
上式中R、θ、λ为球坐标系下的三个坐标线。
因轴对称时，且物理量只在R、θ方向上有变化，故有ψ3=ψ。
同时可得R、θ坐标线上的速度分量(3)这对小雷诺数下的圆球绕流，上述沉降分析是合适的。
恒定流情况有惯性项均可忽略。
对于外部绕流，流函数是无源场，则有，因此可得。
此时流函数与涡量的关系方程。
如果是轴对称流动，则涡量只有3=Ω 为标量，流函数亦只有ψ3=ψ也为标量，而有Ω+Δ2ψ=0(4)即在小雷诺数时，对轴对称的圆球绕流，解Navier-Stokes方程，可变为解流函数ψ满足的重调和方程▽2▽2ψ＝0。
3 单个球形颗粒在粘性流中匀速沉降解单个球形细颗粒在粘性流中匀速沉降的速度ω0，可从流体力学分析得到。
单个球形颗粒在粘性流中绕流时，其Stokes流函数为ψ=1/4Vsin2θ（α3/R－3αR+2R2）。
如将球坐标原点放在球心，利用(3)式，可得圆球绕流时R、θ坐标线上的流速分量分别为(5-1)(5-2)通过对作用于球面上的压力积分，可求得圆球所受阻力为3πμdV，其中V为球与流体的相对速度，当球体均匀沉降时，有效重力(γs-γ)πd3/6与阻力相平衡。
其中球体半径为α，直径为d。
一个球体直径为d所占的距离为d+l，N个均匀颗粒占的距离当N(d+l)。
一个球体体积为πd3/6，N个πd3/6，所占空间为N3(d+l)3，体积比浓度(6)当l d时，则S v→0；当l→0，均匀沙排列均匀，得S v=0.5236。
此为极限浓度S vm的下界，随机紧密填充可达S v=0.5612，如果为非均匀沙随机排列，该值还可以再取高一些。
如S vm≈0.65，但只要达到这种情况，流体将很难在颗粒间流动，因此，此下极限浓度值也是可用的，随着l/d的改变，浓度值变化如表1所示。
表1 浓度S v随l/d变化Table 1 Concentration S v change with the variable l/dl/d 100501075 2.710.50.30.24×10-40.0010.0240.010.06550.1550.23830.303S v0.5×10-50.4×10-5不论如何，只要我们随机地给出粒径大小d与它所在位置，我们可以求得其它函数ψ及阻力值。
因为对于Stokes解，可以按奇异子线性叠加而得，可数值求解。
而对于过渡区及紊流区，则非理论可解，而由实验决定。
随着浓度Ｓv的增加，颗粒沉速有由过渡区趋向滞流区，紊流区趋向过渡区的趋势，因此重点放在理论分析滞流区沉降是合适的。
4 现有的群体沉速公式目前，对单颗粒泥沙在静水中的沉降规律己基本掌握，但对群体颗粒的沉降规律还有待于深入研究。
前人对颗粒群体沉速公式的研究，可大致划分为两类：一是粗颗粒均匀沙的沉速，二是含较多细颗粒的非均匀沙沉速[1]。
(1)Batchelor(1972)认为球体在低含沙水体中沉降时，颗粒间及颗粒与周围水体的相互影响，其沉速与其在无限清水中沉速的差异，是平均值不为0的随机变量[3]。
他从统计理论出发，最后推导出低含沙量情况下群体沉速的理论公式 ωs/ω0=1－6.55S v(7)上式中当S v≤0.05时，计算结果能与实验值基本符合；当S v较大则偏差大。
(2)Richardson和Zaki 采用量纲分析与试验结果，建立如下群体沉速公式[4]ωs/ω0=(1-S v)m (8)上式中指数m与沙粒雷诺数(Re d=ω0d/ν)有关。
夏震寰和汪岗对细沙取m=7时，上式与试验资料符合较好[5]。
(3)王尚毅认为式(8)中当S v=1时ωs=0，这种计算结果不对[6]。
因此将上式修改为ωs/ω0=(1-βS v)m (9)上式中m=2.5；β与泥沙特性有关，对塘沽淤泥可取β=5.0。
(4)钱意颖等人认为群体沉速的减小主要由于浑水的容重与粘度变化所致，得出了适用于层流区的群体沉速公式[7](10)上式中γ、γs、γm分别为清水、泥沙及浑水的容重。
(5)万兆惠等人认为细的单颗粒泥沙在清水中下沉时有(γs-γ)πd3/6=3πdμ0ω0。
当为浑水时，上式仍成立，不过应以μm代替μ0,γm代替γ，ωs/(1-S v)代替ω0。
如浑水粘度采用日本森氏公式μm/μ0=1+3S v/(1-S v/0.52)，代入上式可得群体沉速公式[8]ωs/ω0=(1-S v)2/[1+3S v/(1-S v/0.52)] (11)(6)沙玉清认为在层流区，主要是浑水的粘度影响泥沙沉速，因此可得如下群体沉速公[9](12)上式中d50取mm，且对d50在0.010mm附近的非均匀沙适用。
(7)费祥俊认为用非均匀沙的中值粒径或平均粒径作为代表粒径，按均匀沙方法计算非均匀沙的平均沉速，将会导致较大的误差。
因此应按各粒径组泥沙所占的比例，加权平均后得到非均匀沙的平均沉速公式［10］(13)式中ΔP i为第d i粒径组泥沙所占的比例。
浑水粘度μm与含沙量大小和极限含沙量有关[11]。
(8)张红武在沙玉清公式基础上，考虑到沉降过程中一部分清水将依附沙粒同时下沉，结合试验结果，经推导得出如下群体沉速公式［２］(14)上式中d50同样取mm。
但该式适用范围比沙玉清公式大，近些年多用之于黄河泥沙数学模型计算。
经数值计算我们发现，用式(14)计算群体沉速，必须使。
5 本文的研究结果我们认为群体沉降公式在理论上要尽量合理，尽可能地有严格的两相流体力学的依据，量纲上要和谐，同时计算结果要与实测资料基本符合，才可用于实际计算。
对于本文提出的群体沉速公式，作以下分析与论证。
5.1 颗粒表面流速的分析从泥沙颗粒在浑水中受力情况进行分析：细颗粒泥沙沉降时阻力符合Stokes 公式的单个颗粒沉降规律，为此多个颗粒的阻力解是可以叠加的，只要是散粒体。
我们可以在计算机上，做出随机变化的有限多个(1012～1015个)泥沙颗粒，粒径为0.10～0.01mm不均匀随机分布的泥沙颗粒受流体力的作用，从而得到由于泥沙下沉对周围流场的影响，这一影响并非简单地打一个(1-S v)的折扣，而是对于周围流场的干扰，改变流函数、流线疏密形状的结果。
由流速uθ公式(5)中，可以看出：当R=a处，uθ=0，当R》α时，θ=90° 时，，uθ=V，这说明颗粒对流场有干扰，颗粒扰动形成流核，远处R>10α时，uθ=V=ω0，流速等于沉速，球体匀速沉降，而当l不太大时，对uθ有一定影响。
例如：当l=2α,R+l=3α时，即ωs/ω0=0.74；当l=α时，R+l=2α时，即ωs/ω0=0.577；当l=0.1α,R+l=1.1a 时，则ωs/ω0=0.131。
这些都说明浓度S v的影响实质是对流场的影响。
流体被干扰的流核，使其在一定柱状范围，要带动一定量的流体运动，其相对运动速度(沉速)降低了。
这一结果反映于(15)式中。
5.2 浓度对群体沉降的影响浓度对颗粒沉降影响的研究，最早是1906年A.Einstein从Brown运动得到一阶近似的理论结果，即μm/μ=1+2.5S v［12］。
1972年Batchelor等人得到浓度影响的二阶近似理论结果(球体散颗粒)，相对粘性μr=μm/μ0=1+2.5S v+7.6S2v［３］。
本文认为低浓度时的粘度改正应小些，高浓度时的粘度改正大些，非线性二阶式优于指数关系。
图1给出了各家相对粘度公式的对比结果，可以看出Batchelor的二阶式居中。
考虑到群体沉降的极限浓度S vm及非均匀沙的颗粒组成的影响，本文给出的泥沙颗粒的群体沉降公式有如下形式(15)图1 相对粘度μr与体积比浓度S v关系(牛顿体)Fig.1 Relationship between relative viscosity μr andvolumetric concentration S v上式中α为一修正系数，与混合沙的非均匀程度有关，对均匀沙，可取α=1。
当S v较小时，ωs对ω0改正不大，这是合理的，且ωs/ω0值大些。
在中等浓度S v 下，则ωs/ω0偏差大些，在高浓度S v时，各家差别更大，如(12)式、(14)式很快降为零。
