下载文档原格式
中南民族大学最优组队问题模型摘要本文针对组队问题，运用层次分析法，进行动态规划问题分析，通过计算机算法，分别进行了优秀组员的选取，合理、公平化的人为定组，动态的轮流选组员过程，并最终得到了最佳选人，分配方案。
针对问题1，我们根据常理，明确题目中六个指标对建模能力的影响显然是不同的，但是我们只能从定性的角度来分析哪些因素对建模能力素质影响较大。
于是我们建立出求加权平均成绩的函数模型1然后经过Excel计算排序之后，得到加权平均水平统计表，进行了人员的直接筛选。
但这种方法是占很大主观因素的，也缺乏一定的公平性。
因此，我们建立了模型2，运用层次分析法，依次求解出目标层（18名选拔出的学生）、准则层（6项评价水平）、方案层（20名学生）之间的权重，最终根据每位同学所占的权重大小来筛选出优秀的学生。
针对问题2，我们首先确定出三人组队选拔的最低标准。
每三个人的每项能力的最大值都必须大于设定的最低标准,这样三个人才准许组成一队,因为三个人作为一整体,决定他们的能力水平的是这三人每项能力的最高水平，而不是取决于每队的最低水平。
所以每一组的能力由团队中在这方面最优的选手决定，所以在组队的过程中，每队的三名选手至少有两项能力在整体平均能力以上，根据这一原则以及综合水平尽可能高进行组队。
然后通过计算机算法，对这一问题进行实现。
最终确定分组为：第一组：1,6,7;第二组：2,11,12；第三组：5,13,14,；第四组：3,15,16；第五组：4,19,20；第六组：10,17,18针对问题3，它是一个典型的动态规划问题，问题的难处在于教练的决策互相影响，每位教练在每步的决策都受到当前局势的影响，如果所有教练仅仅想要各项指标加权平均后取最大值，显然可能出现一队中三名选手均在某一方面（比如说写作能力）很擅长，但其他方面很欠缺。
所以教练应着眼于让自己的某位选手，在某两方面很擅长，而且整队各个方面都很有实力。
在每一轮教练都是选当前所有选手各项水平最靠前的那位选手。
数学建模队员的选拔及组队问题研究013082组 黄梦遥 朱文意 李培一一、摘要全国大学生数学建模竞赛[1]（以下简称“国赛”）是全国高校规模最大的课外科技活动之一。
数学建模是一种运用数学语言和方法，通过抽象、简化建立模型，能近似刻画并“解决”实际问题的强有力的数学手段。
数学建模在物流、交通等领域中日益广泛的应用对数学建模竞赛产生了很大的促进作用。
由此，各大高校也越发看重学生在这项大赛中取得的成绩，如何选拔参赛队员以及如何合理组队这些问题就显得非常重要。
本文以清晰的思路建立了数学模型，并对模型做了合理的假设，对队员选拔、成员组队等问题进行了较为深入的探讨，并提出了模型的解答。
1.每名队员的优势能力不同，问题一要求我们在这20名队员中做出取舍，我们想到了用层次分析法。
我们给各项能力按照题目的要求合理地给定了权重，并按照层次分析法的步骤利用MATLAB 计算出了每名队员的综合实力，在Excel 中按降序排列，8、9两名队员是最后两名，因此落选。
我们又想到了每学期期末考试后我们计算平均学分绩的方法，对20名队员的能力进行了简便的直接加权，那么每名队员的综合实力可表示为：6161i S jjj i jj bw m w===∑∑同样按照降序排列，淘汰8、9两名队员。
2.对问题二，我们有两个思路。
思路1.用逐项选优方法，用目标函数()6,,,,1,k l mk l mS S S S S S jj jj j f bw b w ==∑表示成员编号为k l m S S S 的队伍的整体竞赛水平：。
利用上述目标函数在18名队员中找到3个人，使队伍整体竞争水平最高，接着按以上方法依次选队员，直到18名队员分成6组。
思路2.用仿真法，使得六个组的平均竞赛水平达到最大值并且六个组的竞赛水平方差最小。
首先将18名队员按综合实力降序排名分成人数相等的三组，三组中各取出一名队员使之组成一支参赛队伍，用MATLAB 编程，取10万个可能的组合，由此计算出使得六个组的平均竞赛水平最高且各组水平最均衡的分组情况。
数学建模竞赛参赛队员选拔组队问题摘要本文以一年一度的全国大学生数学建模竞赛活动为背景，研究了我校如何选拔最优秀的队员和科学合理地组队问题。
选拔队员主要参考三个环节：(1)校数学建模公选课成绩；(2)校内数学建模竞赛成绩；(3)按照一定的准则教师对每个学生的某些能力和素质给出一个等级评分。
首先根据上面的三个环节从25名学生中选出18名优秀学生分别组成6个队，每个队3名学生去参加比赛。
然后再考虑环节(3)中的各能力素质在数学建模竞赛中的重要性，设计出两种组队方案，使获奖最大化。
最后综合考虑该问题中的所有影响因素，提出了一些自己的建议。
针对问题一：我们首先对题目所给表格中数据合理量化，然后将量化后的数据再归一化处理，采用层次分析法获得各位同学的各项参考指标的权重，再加权求和得到综合得分并排名，最后选出前18名优秀学生，从高到低依次为：学生4，学生16，学生6，学生5，学生14，学生2 ，学生11，学生7，学生21，学生13，学生3，学生9，学生8，学生1 ，学生12，学生25 ，学生18，学生23。
针对问题二：我们首先用层次分析法得到各项能力素质对获奖影响的权重大小，并根据权重大小对各项能力素质进行排序。
然后深刻理解问题要求“获奖最大化”一词的涵义，我们理解为：使获奖名次尽可能的高，以及获奖组数尽可能的多。
最后，根据我们的理解，设计出两个最佳组队方案，即：先选出一个各项能力素质最佳的队既能确保竞技水平最高，又能充分利用优势使其他组队能力提高，进而达到整体水平提高的目的。
再在剩下的15名学生中按方案一：考虑每一组的实力尽可能相同，将能力高的同学与能力低的同学进行优劣互补，取长补短，将6个队的整体水平提到一个高度。
方案二：考虑获奖等级越高越好，，将各项能力最强的学生选出，再组队求出综合得分并排序，由高到低依次组队（每人只能入一个队）。
结果为：方案一分组方案二分组针对问题三:根据选拔与组队的需要，结合实际情况，考虑对建模选拔的其他因素，结合模型一、二，向建模教练组提供一些建议。
数学建模比赛的选拔问题卢艳阳 王伟 朱亮亮（黄河科技学院通信系，）摘 要本文是关于全国大学生数学建模竞赛选拔的问题，依据数学建模组队的要求，每队应具备较好的数学基础和必要的数学建模知识、良好的编程能力和熟练使用数学软件等的综合实力，在此前提下合理的分配队员，利用层次分析法，建立合理分配队员的数学模型，利用MATLAB ，LONGO 工具求出最优解。
、问题一：依据建模组队的要求，合理分配每个队员是关键，主要由团队精神、建模能力、编程能力、论文写作能力、思维敏捷以及数学知识等等，经过讨论分析，确定良好的数学基础、建模能力，编程能力为主要参考因素。
问题二：根据表中所给15人的可参考信息，我们对每个队员的每一项素质进行加权，利用层次分析法选出综合素质好的前9名同学，然后利用0-1规划的相关知识对这9人进行合理分组，利用MATLAB 、LINGO 得到其中一个如下的分组：'1s 、10s 、4s ；2s 、11s 、14s ；6s 、13s 、8s问题三：我们将所选出的这9名同学和这个计算机编程高手的素质进行量化加权，然后根据层次分析法，利用MATLAB 工具进行求解，得出了最佳解。
由于我们选取队员参考的是这个人的综合素质，而不是这个人的某项素质，并由解出的数据可以看出这个计算机编程高手不能被直接录用。
所以说只考虑某项素质，而不考虑其他的素质的同学是不能被直接录用的。
问题四：根据前面三问中的分组的思路，我们通过层次分析法先从所有人中依据一种量化标准选出符合要求的高质量的同学，然后利用0-1变量进行规划，在根据实际问题的约束，对问题进行分析，然后可以得出高效率的分组。
关键字：层次分析法加权量化0-1变量LINDO MATLAB问题重述一年一度的全国大学生数学建模竞赛是高等院校的重要赛事。
由于竞赛场地、经费等原因，不是所有想参加竞赛的人都能被录用。
为了能够选拔出真正优秀的同学代表学校参加全国竞赛，数学建模教练组需要投入大量的精力，但是每年在参赛的时候还是有很多不如意之处：有的学生言过其实，有的队员之间合作不默契，影响了数学建模的成绩。
数学建模竞赛参赛队员组队问题摘要本次建模中要解决的是参赛队员的组队问题，在本次建模中主要用到的是层次分析法，以及求权重的方法从而确定主成分因素。
并且用Excel分析数据，Matlab 编程，得到所需数据。
问题一中，一、问题重述全国大学生数学建模比赛是由教育部发起的18项大学生创新训练项目之一，目前已为广大大学生所熟悉。
目的在于激励学生学习数学的积极性，提高学生建立数学模型和运用计算机技术解决实际问题的综合能力，鼓励广大学生踊跃参加课外科技活动，开拓知识面，培养创造精神及合作意识，推动大学数学教学体系、教学内容和方法的改革。
河海大学常州校区每年都会有一定数量的学生参加此项赛事，并取得了一定的成绩。
为此，数理部每年暑期将会对学生进行培训，最后选拔出参赛的队员。
选拔条件为：思维活跃、编程能力强、熟练的写作技巧、良好团队合作意识。
今已选拔了30名队员参加比赛，要将他们分为10个队，每队3人。
组队原则如下：尽可能地不同学院、不同性别，如果同一学院，尽可能地不同专业，每个队伍中，至少一个人能胜任编程、想法、写作中的一项。
分组依据的条件为：编程、想法、写作、数学能力等。
每个队员的基本条件量化后如附录中的表（一）所示，现假设所有队员接受了相同的培训，外部环境相同，竞赛中不考虑其它的随机因素，竞赛水平的发挥只取决于表中所给出的各项条件，并且参赛队员都能正常发挥自己的水平。
现在要解决的问题有三个：第一，根据所了解的数学建模的知识，选拔数学建模队员需要考虑学生的哪些方面的情况，哪些素质是数学建模的关键素质，并且是如何考虑的；第二，在表（一）中的30名队员，组成10支队伍，给出组成每队实力相当的方案；第三，给出竞赛获奖最大化的组队方案；第四，表（一）中没有给出团队意识的量化数据，如果要考虑这一因素，又将如何建立数学模型。
二、模型假设1、假设问题给出的数据均为可供分析的可靠数据，不存在错误数据。
2、假设每个队员接受相同的培训，相同的外部环境，在参赛过程中不考虑随机因素。
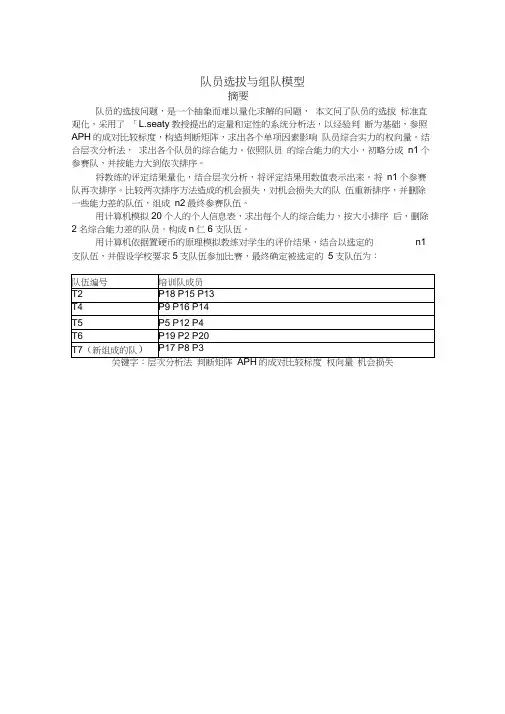
队员选拔与组队模型摘要队员的选拔问题，是一个抽象而难以量化求解的问题，本文问了队员的选拔标准直观化，采用了「L.seaty教授提出的定量和定性的系统分析法，以经验判断为基础，参照APH的成对比较标度，构造判断矩阵，求出各个单项因素影响队员综合实力的权向量。
结合层次分析法，求出各个队员的综合能力。
依照队员的综合能力的大小，初略分成n1个参赛队，并按能力大到依次排序。
将教练的评定结果量化，结合层次分析，将评定结果用数值表示出来。
将n1个参赛队再次排序。
比较两次排序方法造成的机会损失，对机会损失大的队伍重新排序，并删除一些能力差的队伍，组成n2最终参赛队伍。
用计算机模拟20个人的个人信息表，求出每个人的综合能力，按大小排序后，删除2名综合能力差的队员。
构成n仁6支队伍。
用计算机依据置硬币的原理模拟教练对学生的评价结果，结合以选定的n1支队伍，并假设学校要求5支队伍参加比赛，最终确定被选定的5支队伍为：关键字：层次分析法判断矩阵的成对比较标度权向量机会损失一. 问题重述面对每年一次的全国大学生数学建模竞赛及美国大学生数学建模竞赛, 学校需要花费较多的人力以及财力从报名的学生中选拔出优秀的学生并组成具有竞争力的参赛队, 期望获得最好的成绩.数学建模竞赛的每一个参赛队由3 名同学组成, 要求在三天的时间内完成一个实际问题的求解, 包括问题描述、问题分析、建立模型、模型求解算法设计、编写程序求得结果、模型以及算法改进、模型稳定性分析、优缺点分析，最后撰写论文等。
竞赛过程中仅允许本队队员之间讨论，并可以利用图书馆中的图书资料以及网上的正确可靠资源。
为最终组成有竞争力的参赛队, 计划分两步来挑选队员, 具体如下: 第一步依据报名表中的信息挑选出优秀的学生，并3人一组组成n1个培训队。
报名表（附件4）。
第二步对挑选出的队员进行培训。
在培训期间要经过3 至6次的模拟竞赛，m 个教练对每一个培训队的每一次竞赛都有一个综合评价和单项评价，单项评价包括写作水平、模型的正确性和简洁性、算法的正确性和复杂度、创新点共四项，评价成绩分为：优秀、优良、一般。
《数学建模课程设计》报告课程设计题目：最佳组队问题摘要针对问题1，我们知道题目中六个指标对建模的影响显然是不同的，但是我们只能从定性的角度来分析哪些因素对建模能力素质影响较大。
于是，我们建立出求加权平均成绩的函数模型1然后经过Excel 计算排序之后，得到加权平均水平统计表，进行了人员的直接筛选。
但这种方法是占很大主观因素的，也缺乏一定的公平性。
针对问题2，我们运用层次分析法，依次求解出目标层（12名选拔出的学生）、准则层（7项评价水平）、方案层（18名学生）之间的权重，最终根据每位同学所占的权重大小来筛选出优秀的学生。
针对问题3，我们首先确定出三人组队选拔的最低标准。
每三个人的每项能力的最大值都必须大于设定的最低标准,这样三个人才准许组成一队,因为三个人作为一整体,决定他们的能力水平的是这三人每项能力的最高水平，而不是取决于每队的最低水平。
所以每一组的能力由团队中在这方面最优的选手决定，所以在组队的过程中，每队的三名选手至少有两项能力在整体平均能力以上，根据这一原则以及综合水平尽可能高进行组队。
然后通过计算机算法，对这一问题进行实现。
关键字：层次分析法动态规划问题建模一问题重述2014年美国大学生数学建模竞赛将于美国东部时间2014年2月6日晚上8点举行,任何一个参赛院校都会遇到如何选拔最优秀的队员和科学合理地组队问题这是一个最实际的,而且首先需要解决的数学模型问题.现假设有18名队员准备参加竞赛,根据队员的能力和水平要选出12名优秀队员分别组成4个队,每个队3名队员去参加比赛,选拔队员主要考虑的条件分别为有关学科成绩(平均成绩)、智力水平(反映思维能力、分析问题能力和解决问题能力等)、动手能力(计算机的使用和其他方面实际操作能力) 写作能力、外语能力、协作能力(团结协作能力)和其他特长.每个队员的基本条件量化后如下表所示，根据表中的数据建立数学模型，试回答如下三个问题：1) 选择哪12名优秀队员参加竞赛？2) 确定一个最佳的组队使竞赛技术水平最高；3) 给出由12名队员组成4个队的组队方案，使整体竞赛技术水平最高，并给出每个队的竞赛技术水平。
数学建模选拔队员问题【摘要】全国研究生数学建模竞赛是一项关系到学校和个人荣誉的比赛,因此一个参赛院校如何选拔最优秀的队员和科学合理地组队是一个亟待解决的问题。
我们建立模型解决数学建模队员选拔与组队问题。
第一，队员选择模型。
首先，我们将所给队员的七项基本条件指标划分为知识、能力、表现三类。
运用层次分析法，建立成对比较矩阵，得到三类的权重继而得到七项条件的权重。
然后采用模糊物元法,计算每位队员各项指标的联系系数，并与权重结合得到队员的联系度，依此排名,淘汰排名最后的五位队员。
第二，最佳组队模型。
首先对于某些互补性的条件指标，取三名队员的最大值作为整队指标；对于某些整体性的条件指标，取三名队员的平均值作为整队指标。
然后结合各指标权重建立竞赛水平函数，同时对每项指标进行一定约束。
最后通过Mａｔlaｂ软件计算，求得最佳组队队员。
【关键词】选拔队员与组队层次分析法模糊物元法竞赛水平函数1 引言数学建模竞赛要求以不超过三人的团队参加，其主旨为培养学生的创新意识和团队精神。
这是一项关系到学校和个人荣誉的比赛,因此一个参赛院校如何选拔最优秀的队员和科学合理地组队是一个亟待解决的问题。
目前，２01２年浙江师范大学有２6名队员准备参加竞赛,已知每位队员的平时成绩、智力水平、计算机能力、参赛经验、写作能力、协作能力、身体状况。
假设所有队员接受了同样的培训,不考虑其他随机因素的影响，我们建立数学模型解决如下问题:1．在26名队员中选择２1名优秀队员参加竞赛；2.确定一个最佳的组队方案使竞赛技术水平最高。
2 模型假设1.假设所有队员接受了同样的培训,不考虑其他随机因素的影响;假设层次分析求权重带来的主观因素影响不会有太大影响；３符号说明符号说明A、B 成对比较矩阵a表示第i个因素相对于第j个因素的比较结果ijCI 一致性检验指标数ＲI 随机一致性指标ＣＲ一致性比率ω指标权重 i M方案 j C 特征评价指标 ji x指标量值 max ji xx ｊi 的最大值 min ji xx ji 的最小值 ξ关联系数i ω各个条件指标的权重系数1,2,...,7k l mi i ia a a i =、、（）随机取三个人,,k l m 的第i 项条件的联系系数1,2,...,5i p i =（）第i 项条件联系系数的最大值 6,7i q i =（）第i 项条件联系系数的平均值f竞赛水平函数4 队员选择模型我们在选拔数学建模队员时，一个队员的能力是可以从多方面衡量的,比如计算机能力，智力水平,写作能力等。
选拔队员与组队问题摘要：我们通过对每个队员的基本条件进行分析，我们采用了两种方案解决问题。
方案一：考虑队员的个人竞赛技术水平建立模型一，在模型一的基础上，考虑每个对竞赛技术水平建立了非线性优化模型二和模型三。
问题一：通过建立层次模型，计算每个基本条件对队员的竞赛技术水平的权重(0.3649,0.2479,0.1593,0.0999,0.0622,0.0398,0.0261)Tω=，然后得到每个队员的竞赛技术水平并对其排序（见表二），确定被淘汰的队员为H和I。
问题二：通过模型二求得：把G，L，S这三个队员组成一队时，其竞赛技术水平最高值为：9.588150。
问题三：通过模型三我们求得：使整个竞赛技术水平最高的组队方案。
第一队：A，B，L；第二队：E，F，N；第三队：D，J，S；第四队：K，M，R；第五队：G，O，Q；第六队：C，P，T；每个队的竞赛技术水平的值分别为：9.138，8.9618，9.05707，9.36774，9.32846，9.13068。
方案二：考虑每个队的整体竞赛技术水平建立模型四，得到组队方案为第一队：E，F，S；第二队：I，J，K；第三队：B，G，P；第四队：C，N，R；第五队：G，O，Q；第六队：H，L，T；每个队的竞赛技术水平的值分别为：9.133，8.572，9.265，8.844，9.5，9.392。
淘汰的队员为A和O。
在模型四的基础上求解模型二得到：把H，L，G这三个队员组成一队时，其竞赛技术水平最高值为：9.620。
关键字：层次分析法、优化、权重，竞赛技术水平。
Abstract:We have analysed by being in progress to every Y oung Pioneer's main conditions , we have adopt two kinds schemes to solve a problem.Scheme one: Think that Y oung Pioneer's individual contest engineering level builds a model one, think that every has built nonlinearity optimization model two sums models to contest engineering level in the model on one's basis, three.Question one:By the weight building arrangement of ideas model , calculating every main conditions to Y oung Pioneer's contest engineering level,and then, the contest engineering level getting every Y oung Pioneer and Y oung Pioneer who orders the person (be expressed two) , ascertains that to be sifted out are H and I.Question two:By the model, two asks for: When this three Y oung Pioneer are composed of one team with G , L , S, whose maximal contest engineering level value is: 9.588150. Question three:Pass a model three we ask for: Use the team of maximal group of entire contest engineering level scheme. The first team: A , B , L; Second team: E , F , N; Third team: D , J , S; Fourth team: K , M , R; Fifth team: G , O , Q; Sixth team: C , P , T; Every team's contest engineering level value is respectively: 9.138 , 8.9618 , 9.05707 , 9.36774 , 9.32846 , 9.13068.Scheme two:Think that every team's overall contest engineering level builds a model four, are formed the team scheme for the first group: E , F , S; Second team: I , J , K; Third team: B , G , P; Fourth team: C , N , R; Fifth team: G , O , Q; Sixth team: H , L , T; Every team's contest engineering level value is respectively: 9.133 , 8.572 , 9.265 , 8.844 , 9.5 , 9.392. Y oung Pioneer who is sifted out is A and O.Find the solution in the model on four's bases model two: When this three Y oung Pioneer are composed of one team with H , L , G, whose maximal contest engineering level value is: 9.620. Key words:Arrangement of ideas analyses law , optimization , weight , contest engineering level.一问题重述在一年一度的美国MCM和全国大学生竞赛活动中，任何一个参赛院校都会遇到如何选拔队员和科学合理的组队问题。
数学建模竞赛参赛队员的选拔与组队摘要如何选拔最优秀的队员并科学合理的组队，是一个非常具有实际意义的数学模型问题。
本篇文章根据实际数据，综合考虑各方面因素的影响，给出了可以判断队员组队情况好坏的一般规律，并联系实际，运用所得规律进行科学的预测。
为了给出可以判断队员组队情况好坏的一般规律，本文综合考虑队员的性别、所属学院类型、在校期间的成绩。
为了分析前两者的影响，本文对三类（获国家奖、获省奖、没获奖）队伍的性别分布及所属学院类型分布进行了对比。
发现：规律1：队员不同的性别组合对数学建模成绩没有显著影响。
规律2：三个队员中至少有两个来自理工类学院时，组队效果好。
三个队员都来自文科类学院，组队效果不好。
在分析成绩的影响时，首先，联合使用计算机筛选（以课程开设学院为筛选依据，仅筛选出统计与数学学院、计算机与信息工程学院、人文学院、马克思学院开设的课程）与人工筛选，选出每个人学过的能反映数学建模能力的所有课程。
根据实际经验，数学建模是数学能力、计算机能力和写作能力的综合运用，利用筛选出的成绩可以对每个人的各项能力进行量化。
而后，为了得到衡量数学建模综合能力的指标，本文利用层次分析法求解出数学能力、计算机能力、写作能力对数学建模综合能力的权重分别为0.5396、0.2969、0.1634。
文中使用了两种方法确定了两个综合能力指标，其一为队伍能发挥的最大综合能力，该指标下每个队伍的单项能力为三个队员该项能力的最大值；其二为平均综合能力，该指标下每个队伍的单项能力为三个队员该项能力的平均值。
经过对比，得到如下规律：规律3：队伍能发挥的最大综合能力越高，组队效果越好。
队伍能发挥的最大综合能力低于80.6时，组队效果不好，高于90.69时，组队效果非常好。
规律4：队伍能发挥的平均综合能力越高，组队效果越好。
队伍能发挥的平均综合能力低于75.32时，组队效果不好，高于88.48时，组队效果非常好。
根据以上规律对问题二的5支队伍进行预测，发现：这5支队伍都有很大的几率获奖（国家奖或省奖），X1很有可能获得国家奖，X5最好成绩应该为省奖。
数学建模队员选拔和组队问题摘要组队问题是历来数学建模的一大难题。
本次建模中要解决的就是参赛队员的选拔与组队的问题，在本次建立的模型中主要用到的是层次分析法，以及求权重的方法从而确定主成分因素。
并且用Excel分析数据，Matlab编程，得到所需数据。
在问题一中，对于队员选拔的问题，就模型一而言，按照队员各项能力在综合评价中地位等同，按择优录取原则在Excel中用记权型法得到25名队员的综合排名，自然淘汰最后7名这两位队员。
在模型二中，它采用的是层次分析法，将18个要选出参赛的队员作为目标层O，7个条件作为准则层C，20个队员作为方案层P. 再由成对比矩阵用Matlab计算确定各条件C1，C2,…，C6对上层因素的权重，最后求出组合权向量.在问题二上，在队员组队时，要使获奖机率最大，就模型一而言，按照队员的各能力素质在数学建模竞赛中的重要性排序。
在考虑重要性排序的情况下，给出问题1中18名队员的组队方案。
关键词：层次分析法权重记权型法Excel分析数据MATLAB计算数据.一、问题重述全国大学生数学建模比赛是由教育部发起的18项大学生创新训练项目之一，目前已为广大大学生所熟悉。
目的在于激励学生学习数学的积极性，提高学生建立数学模型和运用计算机技术解决实际问题的综合能力，鼓励广大学生踊跃参加课外科技活动，开拓知识面，培养创造精神及合作意识，推动大学数学教学体系、教学内容和方法的改革。
我校每年都会有一定数量的学生参加此项赛事，并取得了一定的成绩。
在一年一度的竞赛活动中，任何一个参赛院校都会遇到如何选拔最优秀的队员和科学合理地组队问题，这本身就是一个最实际而且是首先需要解决的数学模型问题。
表1里给出了某年的已经选拔出来的学生相关信息，包括：校数学建模公选课成绩、数学建模校内赛名次、编程、创新、写作、专业能力的等级等。
根据所给的信息，进行组队，每队三人，组队原则如下：1)尽可能地三人中的善长项不要重复。
2)每个队伍中，如果善长项重复，至少一个人能胜任编程、创新、写作中的一项。
根据如上要求，完成下面的问题：1、按择优录取原则，在25名学生中，如何选择18名优秀队员参加竞赛；2、给出问题1中18名队员，为了使获奖最大化，如何组队。
二、模型假设1、假设问题1中环节（3）中各项能力在综合评价中地位等同；问题2中环节（3）中各能力素质在数学建模竞赛中的重要性重要性不同。
2、假设一等奖为9.0分，二等奖为8.0分，三等奖为7.0分，成功参赛奖为6.0分，A为9.0分，B为8.0分，C为7.0分，D为6.0分。
3、假设问题给出的数据均为可供分析的可靠数据，不存在错误数据。
4、假设每个队员在参赛以前接受相同的培训，相同的外部环境，在参赛过程中不考虑随机因素。
5、假设相各个队在参赛中之间相互独立，不互影响。
6、假设每个队员都能正常发挥如表中的水平。
三、符号说明四、模型建立及求解通过上述分析假设基础上，解决问题我们建立了三个模型。
1、模型一：假设一等奖为9.0分，二等奖为8.0分，三等奖为7.0分，成功参赛奖为6.0分，A为9.0分，B为8.0分，C为7.0分，D为6.0分。
用Excel处理相关数据，得出下表：平均分8.78.5166678.2166678.2166678.1666678.158.158.0833338.0666678.05由上表不难看出，在25名队员中综合水平最弱的是24、22、20、10、19、17、15这七位队员，因此这七名队员就被淘汰了。
2、模型二：用层次分析法，将18个要选出参赛的队员作为目标层，6个条件作为准则层，18个队员作为方案层。
如下图：根据题意及假设可知，6个条件指标是依次递减的，不妨假设它们相差1.，所以得到如下的正互反矩阵：（见附录程序一）目标层O准则层方案层P ：⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=121314151612121314151321213141432121315432121654321A用Matlab 编程计算特征向量:]0434.0,0655.0,1024.0,1604.0,2488.0,3794.0[0=ω特征值1232.6=λ一致性指标CI （1）=(λ-n)/(n-1)=0.0246随机一致性指标RI （1）=1.2400.一致性检验CR （1）=CI/RI= 0.0198<0.1.通过一致性检验.下面在考虑方案层对准则层的特征向量，设其矩阵为B=（b ij ） i=1,2....18,j=1,2 (6)特征矩阵W=（W ij ） i=1,2....18,j=1,2 (6)该矩阵归一化处理，必定为一致阵.所以λ = 18.所以其CI, RI, CR,都为0.()6...3,2,1.18....3,2,1181===∑=j i b b W i ijijij用Matlab 编程得到下表：（见附录程序二）P-C 层特征向量P-C C1 C2 C3 C4 C5 C6 P01 0.062 0.05 0.0621 0.0552 0.0571 0.053、模型三：要使获奖机率最大，显然要考虑到队员之间的互补性，使该队组在指标上的权重最大. 以及使用逐次优选的思想将剩下的队员组队分成六组。
设立这样一个函数：0T ( ) , 1,2,6i f i ωω=⋅=ω 表示个人对准则层的权重作为个人的水平.P02 0.0607 0.0571 0.0552 0.0552 0.0571 0.0571 P03 0.0607 0.0571 0.0552 0.0483 0.0643 0.05 P04 0.06 0.0643 0.0621 0.0552 0.0643 0.0571 P05 0.0594 0.0571 0.0621 0.0621 0.0571 0.0571 P06 0.0587 0.0643 0.0552 0.0621 0.05 0.05 P07 0.0587 0.0571 0.0621 0.0483 0.0571 0.05 P08 0.0581 0.05 0.0552 0.0552 0.0571 0.0643 P09 0.0574 0.0571 0.0483 0.0552 0.05 0.0571 P11 0.0548 0.0571 0.0621 0.0621 0.0429 0.0571 P12 0.0541 0.05 0.0483 0.0552 0.0643 0.05 P13 0.0541 0.05 0.0552 0.0621 0.0643 0.0571 P14 0.0522 0.0643 0.0552 0.0483 0.05 0.0643 P16 0.0515 0.0643 0.0621 0.0483 0.05 0.0643 P18 0.0509 0.05 0.0552 0.0552 0.05 0.05 P21 0.0502 0.05 0.0552 0.0621 0.05 0.05 P23 0.0489 0.05 0.0483 0.0483 0.0571 0.0571 P25 0.0476 0.05 0.0414 0.0621 0.0571 0.0571五、模型评价优点：本文问题一中的模型一中采用的是用Excel处理数据，此模型比较直观，并且计算也非常简单。
对于模型二，用的是层次分析法，在计算过程中还用到了权重，这样增加了组队的公平性，还建立竞技函数，这样明显的表示除了队员的优劣情况，而且结果也比较合理可信。
缺点：对问题二，没有找到更好的解决方法和解决思想，在解答上计算不够精确，可能存在一定的误差.六、参考文献[1] 李尚志，数学建模竞赛教程，出版地：江苏教育出版社，1996年。
[2] 资源标题数学建模竞赛参赛的队员选拔与组队问题，网址：/download/explain.php?fileid=23927742，访问时间（2013年7月15日）。
七、附录程序一：(层次分析法程序)clear allclose allclca=[1 2 3 4 5 61/2 1 2 3 4 51/3 1/2 1 2 3 41/4 1/3 1/2 1 2 31/5 1/4 1/3 1/2 1 21/6 1/5 1/4 1/3 1/2 1 ]；n=6;(第一步：每一列向量标准化)for i=1:nfor j=1:nx=0;for k=1:nx=x+(a(k,j));endb(i,j)=a(i,j)/x;endendb；(第二步：按行相加)for i=1:ny=0;for j=1:ny=y+b(i,j);endc(i,1)=y;endc；(第三步：得到特征向量)for i=1:nw(i,1)=c(i)/sum(c);endw(第四步：求AW)AW=a*w;(第五步：计算最大特征值)r=0;for i=1:nr=r+1/n*AW(i)/w(i);endr(计算一致性指标CI)CI=(r-n)/(n-1)(计算随机性指标RI)if (n==6)RI=1.24;endRI(计算一致性检验CR)CR=CI/RI程序二：clear allclose allclcA=load ('D:\data.txt');for i=1:18for j=1:6B(i,j)=A(i,j)/sum(A(:,j));endendB。
