数学建模人员选拔
- 格式:doc
- 大小:109.50 KB
- 文档页数:9


数学建模队员的选拔模型班级:12数学(1)班学号:1207021028 姓名:许菁菁摘要:本文通过对学生的综合素质以及专项素质进行比较之后选拔出优秀的同学再进行组队来建立模型。
对于问题(1)属于优化问题,对这20名同学的综合素质,我们利用层次分析法,选出18名同学,并用Excel表格进行整理。
对于问题(2)根据问题一选出的18名同学,通过多他们的专项进行分析得出竞赛水平最高的一组(3人)。
对于问题(3)根据问题一,对这18名同学按照其专项能力求最优组合,利用0-1规划建立模型,并且利用lingo软件求解。
最终分组得出总成绩。
关键词:层次分析 0-1规划 Excel Lingo1 问题重述在一年一度的美国MCM和中国全国大学生数学建模竞赛活动中,任何一个参赛院校都会遇到如何选拔最优秀的队员和合理的组队问题。
这是一个最实际的、而且是首先需要解决的数学模型问题。
现假设有20名队员准备参加竞赛,根据队员的能力和水平要选出18名优秀队员分别组成6个队,每个队3名队员去参加比赛。
选择队员主要考虑的条件依次为有关学科成绩(平均成绩)、智力水平(反应思维能力、分析问题和解决问题的能力等)、动手能力(计算机的使用和其他方面实际操作能力)、写作能力、外语水平、协作能力(团队协作能力)和其他特长。
每个队员的基本条件量化后如下表。
假设所有队员接受了同样的培训,外部环境相同,竞赛中不考虑其他的随机因素的影响,竞赛水平的发挥只取决于表1中所给的各项条件,并且,参赛队员都能正常发挥自己的水平。
现在的问题是:(1)在20 名队员中选择18 名优秀队员参加竞赛;(2)确定一个最佳的组队使竞赛技术水平最高;(3)给出由18名队员组成6个对的组队方案,使整体竞赛技术水平最高;并给出每个队的竞赛技术水平。
表1 队员的基本条件条件数值队员学科成绩(Ⅰ)智力水平(Ⅱ)动手能力(Ⅲ)写作能力(Ⅳ)外语水平(Ⅴ)协作能力(Ⅵ)其他特长(Ⅶ)A 8.6 9.0 8.2 8.0 7.9 9.5 6B 8.2 8.8 8.1 6.5 7.7 9.1 2C 8.0 8.6 8.5 8.5 9.2 9.6 8D 8.6 8.9 8.3 9.6 9.7 9.7 8E 8.8 8.4 8.5 7.7 8.6 9.2 9F 9.2 9.2 8.2 7.9 9.0 9.0 6G 9.2 9.6 9.0 7.2 9.1 9.2 9H 7.0 8.0 9.8 6.2 8.7 9.7 6I 7.7 8.2 8.4 6.5 9.6 9.3 5J 8.3 8.1 8.6 6.9 8.5 9.4 4 K 9.0 8.2 8.0 7.8 9.0 9.5 5 L 9.6 9.1 8.1 9.9 8.7 9.7 6 M 9.5 9.6 8.3 8.1 9.0 9.3 7 N 8.6 8.3 8.2 8.1 9.0 9.0 5 O 9.1 8.7 8.8 8.4 8.8 9.4 5 P 9.3 8.4 8.6 8.8 8.6 9.5 6 Q 8.4 8.0 9.4 9.2 8.4 9.1 7 R 8.7 8.3 9.2 9.1 8.7 9.2 8 S 7.8 8.1 9.6 7.6 9.0 9.6 9 T 9.0 8.8 9.5 7.9 7.7 9.0 62 问题分析每年数学建模比赛都需要选拔出真正优秀的队伍(每组三个人)代表学校参加比赛,来提高获奖的几率。

数学建模竞赛参赛的队员选拔与组队问题数学建模竞赛参赛的队员选拔与组队问题【摘要】本⽂根据竞赛队员的选拔和组队问题的基本要求,制定合理假设并求解。
依据各种能⼒的权重,建⽴能⼒加权值图表,由能⼒加权值排名进⾏参赛队员的选拔。
在确定最佳组队的问题上,⾸先以综合加权能⼒为依据选择,再根据相对优势制定调整⽅案。
为参赛队员组队的⽅案参照了最佳组队的⽅法并进⾏了推⼴,使所有队伍之间能⼒相差降低。
最后,建⽴与最⼤值及差值相关的⽬标函数,将队员组队,并将模型进⾏推⼴和改进。
关键词:加权相对优势差值⼀、问题描述问题描述:在参加数学建模竞赛活动中,各院校都会遇到如何选拔最优秀的队员和科学合理的组队问题。
今假设有20名队员准备参赛,根据队员的能⼒和⽔平要选出18名优秀队员分别组成6个队,选拔和评价队员主要考虑的条件依次为有关的学科成绩(平均成绩)、智⼒⽔平(反映思维能⼒、分析和解决问题的能⼒等)、动⼿能⼒(计算机的使⽤及其他⽅⾯的实际操作能⼒)、写作能⼒、外语⽔平、协作能⼒(组织、协调)和其它特长,每个队员的基本条件量化后如下表(略):(1)在20名队员中选择18名优秀的队员参加竞赛;(2)确定⼀个最佳的组队使得竞赛技术⽔平最⾼;(3)给出由18名队员组成6个队的组队⽅案,使整体竞赛技术⽔平最⾼;并给出每个队的竞技⽔平。
⼆、问题分析:队员选择上,关于队员的选取,要从20名队员中淘汰两⼈。
可采取排名然后去除后两名的⽅法。
根据原表格的数据,队员的评估指标分为了7项。
这7项指标的平均值、波动程度都不同。
因此,每种能⼒的权重不⼀致,因此采⽤表⽰差距的⽅差和原始指标的积来表⽰该队员在这项能⼒上的加权指标。
组队原则上:为了组成⼀个最强的组队⽅案,⾸先从综合加权能⼒的排名⼊⼿,再让每位队员的劣势得以补充。
综合所有的18名队员进⾏分组,可以根据以下原则进⾏分组强弱队员结合,综合实⼒较差的队员要有加权能⼒较强的队员给予补充;强弱能⼒结合,某⼀项能⼒较差的队员要有在该项能⼒较强的队员给予补充;不可以存在弱项,表现在模型⾥即为,各指标的最⼤值均⾮负。




数学建模混合泳接力队选拔摘要本文研究的是体育赛事中混合泳队员的选拔问题。
结合运筹学中的指派问题及应用线性规划理论,我们建立0-1整数规划数学模型,运用MATLAB软件对模型进行求解,得出了较为科学的选拔方案。
为了从5名候选人中选出4名队员组成接力队,参加4×100米混合泳比赛,我们以5位候选人的平时游泳成绩的数据为基础,运用0-1整数规划建立相关的数学模型,求解出乙进行蝶泳→丙进行仰泳→丁进行蛙泳→甲进行自由泳的比赛方案。
此比赛方案下的比赛最佳总得分为z=251.4s。
混合泳的比赛成绩除了和团队的配合及一些外部因素相关外,更与队员在不同时期内的比赛发挥相关。
因此,当候选人的在成绩发生变化时,我们应依据具体情况,优化游泳队的选拔方案。
当然我们的模型也存在不足之处,在模型的改进中提出了改进方法。
关键字:混合泳队员选拔指派问题线性规划理论 0-1规划模型一、问题重述现拟从5名候选人中选出4名队员组成接力队,参加4100 米混合泳比赛。
5名队员的4种泳姿的百米平均成绩如下表:5名队员的4种泳姿的米平均成绩(表一)1.如何选择队员进行接力队才能获得最佳成绩?2.若队员丁的蛙泳成绩退步到1’15”2,戊的自由泳成绩进步到57”5,组成接力队的方案又当如何?二、问题分析混合泳队员的选拔问题中,主要有以下几个难点:①每个队员比赛成绩数据的分析;②每个队员进行哪个项目才能使团队混合泳成绩最佳;③当有队员的一些项目比赛成绩发生变化时,接力队方案如何选择。
因此,在怎样的选拔机制下,如何处理搜集的数据,建立何种数学模型,是我们首先要解决的问题。
对于问题一,如何选择队员进行接力赛才能使团队获得最佳成绩。
根据5名队员4种泳姿的百米平均成绩,由穷举法我们可以计算出最多有120种选拔方案。
假设队员在比赛现场发挥的成绩与其平均成绩一致。
我们结合0-1规划的思想,以混合泳 甲 乙 丙 丁 戊 蝶泳 1’06”8 57”2 1’18’ 1’10” 1’07”6 仰泳 1’15”6 1’06” 1’07”8 1’14”2 1’11” 蛙泳 1’27” 1’06”4 1’24”6 1’09”6 1’23”8 自由泳 58”6 53” 59”4 57”2 1’02”4总成绩最佳为目标函数,依据其各泳姿的百米平均成绩,建立合理的数学模型,由MATLAB 迅速求解选拔方案。

数学建模竞赛选拔说明哇塞!一听到“数学建模竞赛选拔”这几个字,我的小心肝就扑通扑通跳个不停!你们知道吗?这可不像平时做几道数学题那么简单,这简直就是一场超级刺激的“战斗”!就好像我们在玩一个超级大型的解谜游戏。
每一道题都是一个神秘的关卡,需要我们用聪明的小脑袋去攻克。
比如说,给你一堆看似毫无头绪的数据,就像一堆乱麻,让你从中找出规律,建立一个能解释这一切的模型。
这是不是超级难?但也超级有趣!选拔的时候,教室里安静得连一根针掉地上都能听见。
大家都紧盯着题目,眉头皱得能夹死一只苍蝇。
我心里就在想:“这题咋这么难啊!难道是故意为难我们的?”我看看旁边的同学,他咬着笔头,一脸苦相,好像在说:“这啥呀,完全搞不懂!”老师在教室里走来走去,那眼神就像在审视一群即将上战场的士兵。
“你们可得好好加油啊,这是难得的机会!”老师的话就像一阵风,吹得我心里更紧张了。
选拔的题目五花八门,有关于城市交通流量的,有关于商品销售预测的。
就拿城市交通流量来说吧,想象一下,城市的道路就像血管,车就像血液在流动。
我们得找出怎么才能让这血液流得更顺畅,不堵车。
这得多难啊!再说说商品销售预测,这不就跟预测天气似的,一会儿晴一会儿雨,谁能说得准?可我们就得从那些乱糟糟的数据里找出规律,预测未来的销售情况。
在这场选拔中,我感觉自己一会儿像个侦探,到处寻找线索;一会儿又像个建筑师,努力搭建着数学的大楼。
有时候觉得自己快要成功了,结果发现还差得远呢!你们说,这数学建模竞赛选拔是不是一场惊心动魄的冒险?反正我是觉得,就算再难,我也要努力冲一冲!因为这不仅能让我的数学变得更厉害,还能让我变得更聪明、更勇敢!这就是我对数学建模竞赛选拔的感受,你们觉得呢?。

数学建模队员的选拔-层次分析法层次分析法(Analytic Hierarchy Process,简称AHP)是一种多准则决策方法,通过构造层次结构分析问题,通过对于决策中所涉及的因素和目标进行层次分解,将问题的各部分分解成若干层次,在该层次结构中使用定量和定性的方法来描述因素之间的关联和权重。
本文将利用层次结构模型,以及层次分析法,对数学建模队员的选拔进行分析。
层次结构模型在进行数学建模队员的选拔中,影响选拔的多个因素可以构建成一个层次结构模型。
例如:在数学建模队员选拔中,可以将最终选出的队员作为最终的目标,而影响选拔的因素可以分解成以下多个因素:1.专业水平:参赛者们的数学水平、学习能力、逻辑思维等问题。
2.团队合作能力:参赛者是否适应团队合作及与人组队互动等问题。
3.沟通和表达能力:参赛者的表达能力、口头和文字沟通交流等问题。
4.个人素质:如责任感、进取心、合作精神、团队协作精神等。
层次分析法在层次分析法中,问题通常首先进行分层,使用准则、子准则和指标以及目标来描述问题,并按照这种结构构造一个具有层次结构特征的问题描述。
接着,将问题中的各个层次之间的依赖关系描述出来,并将各个准则、子准则、指标和目标的重要性大小转化为数量化的比较关系。
比较矩阵是层次分析法中的核心概念。
比较矩阵是一种用于比较各个因素之间差异的矩阵视图,在比较矩阵中,每一个单元格代表两个不同的元素之间的相对权重。
比较矩阵的各行数值之和为1。
以数学建模队员选拔的专业水平为例:在该因素层面上考虑选择队员是否有良好的数学水平、学习能力、逻辑思维;在这些因素比较中,可以进行两两比较后形成下图所示的矩阵视图。
| 比较矩阵 | 数学水平 | 学习能力 | 逻辑思维 ||--------------|----------|----------|----------|| 数学水平 | 1 | 3 | 5 || 学习能力 | 1/3 | 1 | 3 || 逻辑思维 | 1/5 |1/3 | 1 |上表中的数字代表数量级:按比例表示数据之间的重要程度或优先级,并且满足归一化性质:对于矩阵中的每一列,它们的权重比之和应为1。

【精品】数学建模队员的选拔数学建模是现代科学的重要组成部分,它关乎到科技的发展和国家的竞争力提升。
为了选拔出优秀的数学建模队员,我们学校举办了一次选拔活动。
以下是活动的过程和具体要求:一、选拔要求1. 数学基础扎实。
具有较好的数学素养,对数学知识掌握熟练,能快速准确地运用到实际问题中去。
2. 逻辑思维能力强。
能通过深入分析问题,清晰明了地构建模型,推导和解决问题。
3. 团队合作能力强。
具有良好的沟通合作能力,能够有效地与队友协作,共同完成任务。
二、选拔过程本次选拔活动主要分为三个环节:初赛、复赛和决赛。
1. 初赛初赛主要考察参赛者的数学基础,题目难度适中,内容涵盖代数、几何、概率等多个领域,选手需在限定时间内完成试题。
初赛成绩满足要求的参赛者才能晋级复赛。
2. 复赛复赛主要考察参赛者的团队合作能力和实际问题解决能力。
复赛由出题人出一道实际问题,各组队员需独立进行思考和探讨,在规定时间内完成模型构建、求解和分析,需要所有队员共同完成。
复赛成绩最优秀的队伍将进入决赛。
3. 决赛决赛则是在现场进行的模拟实际情境竞赛,由出题人提供完整的实际问题及相关数据,各队在限定时间内构建模型并给出解决方案,需要考虑模型的合理性、解决方案的可操作性以及方案的可行性等。
经过评分,成绩最优秀的队伍将成为建模队伍的代表,前往参加国际数学建模竞赛等相关活动。
三、竞赛收获1. 丰富科技文化知识,提高数学、计算机技能和素养;2. 获得数学建模竞赛的荣誉称号,为日后的学习、就业和发展提供参考;3. 提高团队协作能力,锻炼解决实际问题的能力,同时也增强了交流沟通、判断决策和组织协调能力等。
通过这次选拔活动,我们选出了一批优秀的数学建模队员,他们在后续的培训中不断深化了对数学建模的理解,提高了自己的能力水平,为将来的国际竞赛打下了坚实的基础。
我们相信,在未来的科技创新中,他们一定能够发挥自己的才华和智慧,为推动科技进步贡献一份力量。
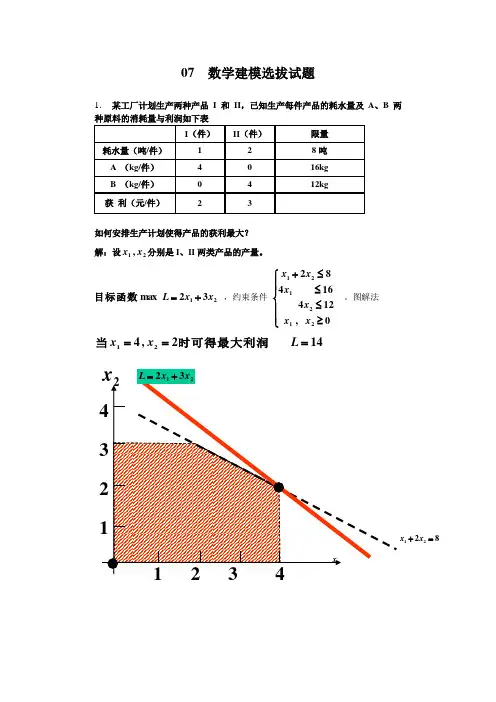
07 数学建模选拔试题1. 某工厂计划生产两种产品 I 和 II ,已知生产每件产品的耗水量及A 、B 两如何安排生产计划使得产品的获利最大? 解:设21,x x 分别是I 、II 两类产品的产量。
2132max x x L +=目标函数,约束条件 ⎪⎪⎩⎪⎪⎨⎧≥≤≤≤+0,12416482212121x x x x x x 。
图解法 142,421===L x x 时可得最大利润当8221=+x x2.设在长江的某一水质观测站测得某种污染物的初始浓度为1000单位,污染物每小时有百分之一被自然降解。
已知长江水的流速为每小时5公里,问在观测站下游x 公里处污染物的浓度为多少? 解:设v ——水的流速(m/h ), C —— 污染物浓度, 0C ——初始浓度k——污染物降解系数,x ——下游与观测站的距离。
设)()(x C t C C ==,由已知条件有微分方程kC dtdC-=。
又因dtdCv dx dt dt dC dx dC ⋅=⋅=1, 则dxdCv dt dC =。
代入到微分方程中去可得 0=+kC dxdCv 。
解得 x vk eC x C -=0)(。
将有关数据代入可得5001000)(x ex C -=。
3. 有一根铁丝绕刚好地球一周,如果把铁丝加长一米,并且均匀分布在地球一周。
问一只老鼠能否从地表和铁丝间穿过,并说明理由。
解:设地球的半径为R ,周长为L ,于是 π2L R =。
当周长增加一米时,半径为 π21'+=L R 。
于是 1592.021221≈=-+=∆πππL L R (米) 。
可以钻过去。
4. 人带着猫、鸡、米过河,船除需要人划之外,至多能载猫、鸡、米三者之一,而当人不在时,猫要吃鸡,鸡要吃米。
试设计一个安全过河方案,并使渡河次数尽量少。
解:过河1 鸡 返回1 空过河2 米 返回2 鸡 过河3 猫 返回3 空 过河4 鸡5. 在线段[0,1]上任意投三个点,问由0至三点的三线段,能构成三角形与不能构成三角形这两个事件中那一个事件的概率大。
数学建模竞赛参赛队员的选拔与组队摘要如何选拔最优秀的队员并科学合理的组队,是一个非常具有实际意义的数学模型问题。
本篇文章根据实际数据,综合考虑各方面因素的影响,给出了可以判断队员组队情况好坏的一般规律,并联系实际,运用所得规律进行科学的预测。
为了给出可以判断队员组队情况好坏的一般规律,本文综合考虑队员的性别、所属学院类型、在校期间的成绩。
为了分析前两者的影响,本文对三类(获国家奖、获省奖、没获奖)队伍的性别分布及所属学院类型分布进行了对比。
发现:规律1:队员不同的性别组合对数学建模成绩没有显著影响。
规律2:三个队员中至少有两个来自理工类学院时,组队效果好。
三个队员都来自文科类学院,组队效果不好。
在分析成绩的影响时,首先,联合使用计算机筛选(以课程开设学院为筛选依据,仅筛选出统计与数学学院、计算机与信息工程学院、人文学院、马克思学院开设的课程)与人工筛选,选出每个人学过的能反映数学建模能力的所有课程。
根据实际经验,数学建模是数学能力、计算机能力和写作能力的综合运用,利用筛选出的成绩可以对每个人的各项能力进行量化。
而后,为了得到衡量数学建模综合能力的指标,本文利用层次分析法求解出数学能力、计算机能力、写作能力对数学建模综合能力的权重分别为0.5396、0.2969、0.1634。
文中使用了两种方法确定了两个综合能力指标,其一为队伍能发挥的最大综合能力,该指标下每个队伍的单项能力为三个队员该项能力的最大值;其二为平均综合能力,该指标下每个队伍的单项能力为三个队员该项能力的平均值。
经过对比,得到如下规律:规律3:队伍能发挥的最大综合能力越高,组队效果越好。
队伍能发挥的最大综合能力低于80.6时,组队效果不好,高于90.69时,组队效果非常好。
规律4:队伍能发挥的平均综合能力越高,组队效果越好。
队伍能发挥的平均综合能力低于75.32时,组队效果不好,高于88.48时,组队效果非常好。
根据以上规律对问题二的5支队伍进行预测,发现:这5支队伍都有很大的几率获奖(国家奖或省奖),X1很有可能获得国家奖,X5最好成绩应该为省奖。
数学建模选拔赛及题目
数学建模选拔赛通常是为了选拔具有数学建模能力和创新思维的参赛者。
每年举办的数学建模比赛都会提供一系列的题目,涉及不同领域和难度级别。
以下是一些可能出现在数学建模选拔赛中的题目类型:
1. 综合评价题:要求参赛者综合运用多个数学概念和方法,解决一个现实生活或工程问题。
这类题目鼓励参赛者灵活应用数学知识,并提供全面的解决方案。
2. 数据分析题:提供一组数据集,要求参赛者进行数据处理、统计分析和模型建立,从中发现规律、做出预测或提供决策支持。
3. 优化问题:给定一个特定的目标函数和约束条件,要求参赛者找到使目标函数最优化的变量取值或参数设定。
4. 模型建立题:要求参赛者根据所给的问题描述,构建一个适当的数学模型,并应用这个模型解决问题。
5. 算法设计题:考察参赛者对于算法设计和优化的能
力,要求设计一个高效的算法来解决一个特定问题。
注意,具体的数学建模选拔赛题目会根据不同比赛的组织者和年份而有所不同。
如果您对某个具体比赛的题目感兴趣,建议您参考该比赛的官方网站或相关资料,以获取最新的题目信息。
数学建模队员的选拔一、摘要本文是一个如何选拔最优秀的队员和科学合理组队问题的数学模型。
此模型我们主要采用的是层次分析法,综合考虑每个学生的指标和整队的技术水平,最终从15名学生中挑选出9名数学建模队员进行参赛,对9名队员进行科学地分组,提出了最佳组队方案,达到更大的获奖几率。
此外,我们还给出一些关于队员选拔的建议。
问题二:选拔队员是一个多目标决策的优化问题,我们采用层次分析法,全面考察了15名学生的七项指标,并按照其对目标层的权重的大小进行了排序,挑选出了排名较前的9名学生进行参赛,他们依次是:S1,S2,S6,S15,S8,S9,S10,S14,S4。
为了能够科学地组队,利用数学软件lingo得到最优组合,如下表:分组队员一队员二队员三该组水平第一组S1 S6 S8 0.2195 第二组S2 S14 S9 0.2097 第三组S15 S4 S10 0.2059问题3:倘若直接录用一个计算机编程高手,不考虑其他方面的情况,我们以机试知识面为计算机编程高手的主要素质,可以在15名学生中挑选出几名能力相似的同学,他们分别为S3、S11、S13和S15,在问题二的结果中,我们可以发现计算机能力强的学生中,只有S15的综合能力排名能进入前9名,其他都被剔除掉,可见,如果只考虑计算机能力这一点,会影响队伍的总体水平,所以该做法是不可取的。
关键词:层次分析法多目标决策最优组合lingo二、问题重述一年一度的全国大学生数学建模竞赛是全国所有高校的重要赛事,如何选拔最优秀的队员和科学合理组队问题是一个首先需要解决的数学模型问题。
我们需要解决以下几个问题:1.根据你们所了解的数学建模知识,选拔数学建模队员要考察学生的哪些情况?哪些素质是数学建模的关键素质,如何进行考察?2.根据上表中信息,建立建模队员选拔的数学模型,从中选出9位同学,并组成3个队,使得这三个队具有良好的知识机构。
3.判断直接录用一个计算机编程高用,而不再考察其它情况这种选拔方式是否可取。
数学建模队员的选拔一.摘要该模型解决了选拔参赛队员及确定最佳组队的问题.该问题涉及面很广,是我们身边经常会遇到的。
本文综合考虑个人的指标以及整队的技术水平,最终从15名队员中选出9名优秀队员,并使得这三个对具有良好知识结构.问题:1。
根据你们所了解的数学建模知识,选拔数学建模队员要考察学生的哪些情况?哪些素质是数学建模的关键素质,如何进行考察?2。
根据上表中信息,建立建模队员选拔的数学模型,从中选出9位同学,并组成3个队,使得这三个队具有良好的知识机构。
在选拔队员时,全面考察了队员的六个指标,并按照相应的权重最后得出15名队员的综合排名,自然最后淘汰掉排名靠后的六名队员,然后在组队。
3.有的指导老师在对学生机试的时候发现一个计算机编程高手,然后直接录用,不再考察其它情况,这种做法是否可取。
4.为数学建模教练组写1份1000-1500字的报告,提出建模队员选拔机制建议,帮助教练组提高建模队员选拔的效率和质量。
关键词:层次分析法;技术水平;逐次选优一、问题的重述现有18名队员准备参加竞赛,根据队员的能力和水平要选出9名优秀队员分别组成3个队,每个队3名队员去参加比赛。
选拔队员主要考虑的条件依次为:笔试成绩、听课次数、思维敏捷、知识面和机试方面的能力以及其他方面的情况。
每个队员的基本条件量化后如表。
假设所有队员的外部环境相同,竞赛中不考虑其它的随机因素,竞赛水平的发挥只取决于表中所给的各项条件,并且参赛队员都能正常的发挥自己的水平。
现在的问题是:1、在18名队员中选择9名优秀队员参加竞赛;2、确定三个组队有较好的知识结构;二、模型的假设1、假设所有队员的外部环境相同,竞赛中不考虑其它的随机因素.2、假设笔试成绩、听课次数、思维敏捷、知识面和机试方面的能力以及其他方面的情况,这六项对队员对影响是占主要的.且影响程度是有所不同。
3、假设竞赛水平的发挥只取决于表中所给的各项条件,且认为表中测量的数据都是客观公正的。
4、假设在组队后各队的发挥是相互独立对,不受其他组的影响。
5、假设参赛队员在正式比赛对过程中都能正常的发挥自己的水平.6、假设组队后的整体水平由该队每项的最佳队员的指标表征.三、符号的说明x1:笔试成绩;x2:机试成绩;x3:思维敏捷;x4 :知识面;x5:听课次数;x6:其他情况。
w1 ,w2 , w3, w4 , w5 , w6表示相应的权系数,y:Sj同学的综合成绩(j=1,2,3…15)jY:第k组的平均成绩(k=1,2,3)kS1,S2……S15 :15名队员的编号四、模型的分析、建立及求解问题一:主要有以下几个方面1抽象分析能力和概括能力,ﻫ2。
观察事物的洞察力3数学知识。
.数学翻译表达能力,数学工具应用能力和软件应用能力ﻫ4。
连续多次推理能力,和想象力ﻫ5.团队精神,团结合作能力和协调能力。
6创造性思维,创新实践能力7。
建模对象的知识.例如物理学,社会学等等。
8。
计算机应用基础,计算机应用能力9自学能力,创新能力和使用文献资料的能力,建模的关键素质自学能力和使用文献资料的能力及意志力、数学应用能力,建模对象的知识。
,团结合作能力和协调能力,抽象概括能力,创造性思维,判断力和洞察力。
如何考察具体来说可以通过情景面试考察;还可以在平时或者课下与学生交流沟通. 硬件方面从知识面,创新能力,数学和计算机基础,计算机应用能力等 软件方面从学生的辩证唯物主义的世界观,人生观,价值观等方面进行考察,还要从心理素质,意志力及综合素质方面考察. 问题二1问题的分析、模型建立与求解这个问题就是在15个队员中剔除6个,显然是要剔除综合实力最弱的六个.然而在考虑这个环节中,是将各项刻画指标按照不同的权重计算后,得出综合成绩,然后对其综合排名,剔除最后的六名即可。
模型:评价指标有六项指标,x1, x2,x3 ,x 4 ,x5 , x 6,他们的权重对应为w 1 ,w 2 , w3 ,w4 ,w 5 ,w6。
.得评价公式:∑==61*n i i j w x y规定:1. A:90——100分,B:80-—90分,C:70——80分,D :60——70分。
w 1=0.2 ,w2 =0.2 , w3 =0.2 ,w 4 =0。
2,w 5 =0.1 , w 6。
=0。
1.2. 各等级取平均分,A:95 , B: 85 ,C:75 ,D:65 。
运用E XCE L求出综合成绩以及综合排名,得表1:目标层O : 准则层C :表1:队员的综合排名作出综合成绩如图1:图1:15名队员的综合成绩图由表可以看出,最后六名是S3 , S5,S7 , S12 , S13 , S15,自然我们就考虑剔除这六名队员。
2。
队员的分配让三个组有良好的知识结构,需要我们对9人综合考虑,不同分组,来判断比较,得出最好的分组.问题转为就是从9名队员中组成3对,目标函数为:Y≈2Y≈3Y1模型:前四项所占的比重都一样,并且每个组都具有良好的知识结构,所以只考虑笔试,机试,平均分这三个方面.现首先把这三项排名,每项取前3名,后面项排名考前中已经有前面3名的,就不再另外考虑,即找剩下队员中最前面的3名。
按照上面思路得前三项指标权重由大到小如表所示:分组如表所示:拟分组计算得出各队的水平为:Y1=84.7 Y2=84。
9Y3=84.1问题三模型假设:计算机水平与综合成绩成线性关系:=y+axb有以下数据:(17,82。
5) ,(17,91.6),(13,73),(17,86), (15,75.4), (17,80.4), (17,78.5) (17,87。
4), (15,81.2), (17,86.9), (19,81.2),(15,76.1),(19,72.9), (17,83.7), (17,75.2)。
根据最小二乘法得到:a=1.06b=63。
2如果该同学的计算机成绩为100分,则他的综合成绩为ﻫy=1。
06*20+63。
2=84.4〉80.4如果该同学的计算机成绩为90分,则他的综合成绩为y=1.06*18+63.2=82。
2〉80.4这位同学的综合成绩大于数模小组综合成绩的最低分80.4,所以这位老师的做法是可取的问题四:数学建模的问题往往不是一个单纯的数学问题,它涉及到其他学科知识以及生活知识。
数学建模的过程是一个多学科的合作过程,它促使学生把从各门课程中学到的知识加以融会贯通;促使学生根据需要查阅资料、获取知识;促使学生围绕问题收集信息,深化对问题的了解,并在此基础上解决问题。
数学建模能力系指对问题做相应的数学化,构建恰当的数学模型,并将该模型求解回译到原问题中进行检验,最终将问题解决或做出解释的能力.阅数学建模的能力包括:阅读理解能力、逻辑推理能力、数学化能力、计算能力和自我监控能力。
将问题数学化,具备使用计算器和计算机加工和处理数学信息的能力,学会设问、提问、探索、合作、交流等。
1、组队原则建模组队,最好是三个人一组,并且来自不同专业。
如果都是同一系,同一专业以及一个班的,这样的组队是不合理的。
让三人一组参赛一是为了培养合作精神,其实更为重要的原因是这项工作需要多人合作,因为人不是万能的,掌握知识不是全面的。
而三个人同系同专业甚至同班的话大家的专业知识一样,如果碰上专业知识以外的背景那会比较麻烦的。
要使各队员的优势得到相互补充,所以如果是不同专业组队则有利的多。
2、队员的能力数学建模特别需要数学和计算机的能力,所以在组队的时候需要优先考虑队中有这方面才能的人,尤其是信息与计算科学可以说是数学和计算机专业,对于弄数学建模来说是再合适不过了。
在组队中有两种人是必需的,一个是对建模很熟悉的,对算法理论熟悉,在了解背景后,对此背景下的各类问题能转化成数学语言,然后建立模型,设计求解算法。
一个是能将算法编制程序予以实现,求得解.第三个就是专门需要写作的同学,编写报告。
建模不仅需要基础能力,还需要其他方面的能力,创新意识、语言表达能力和动手操作能力,形象思维能力等。
老师不能一棍子打死人,要综合整个团体来考虑,使他们能各自发挥特长,建立一个良好的知识结构.3、团队精神数学建模是三人一组,他是一个团队,需要各成员的团结与合作,所以团结精神是一个重要的方面。
团队精神有两层含义,一是与别人沟通、交流的能力;二是与人合作的能力。
队员人的工作能力和团队精神对建模小组而言是非常重要的。
团队创造团队业绩.团队所依赖的是个体成员的共同贡献而得到的实实在在的集体成果。
这里恰恰不要求团队成员都牺牲自我去完成同一件事情,而要求团队成员都能够最大限度地发挥自己的才能和长,去共同完成数学建模任务。
队员的向心力、凝聚力,同合作是取得成功的重要因素,来自于团队成员自觉的内心动力,来自于共识的价值观,他们一个共同的目标并为之而奋斗。
4、如何打造团队精神1、营造浓厚的建模氛围。
一个令人愉快的学习氛围是高效率的一个很重要的影响因素,快乐而尊重的气氛对提高队员积极性起着不可忽视的作用。
如果每一天都要身处毫无生气、气氛压抑的环境之中,那么队员怎么能会积极地投建模工作中呢?2、建立有效的沟通机制。
队员在建模过程中可能会有压抑的感觉,队员之间进行有效的沟通会减少成员的压抑感,促进学习,激起建模的兴趣,这样小组学习起来就容易出成效,目标就能顺利实现。
ﻫ3、不要惩罚学生,否则,学生就会对老师产生不满,甚至是放弃,老师和学生要处好关系。
惩罚导致行为退缩,是消极的,被动的。
激励是积极的、主动的,能持续提高效率。
激励和肯定有利于增强学生对建模的正面认同.来自精神和物质方面的激励会更有效。
特别是关怀、爱心、耐心、善用、信任和尊重。
综上所述,一个建模团队不仅仅考虑基础知识,比如:数学基础,计算机基础,还需要思维创新,知识面宽广,头脑灵活,动手能力强,能与人相处,有团队精神,集体荣誉感强的队员.。