数学建模队员的选拔模型

挑选队员的策略模型摘要全国大学生建模竞赛已成为全国高校规模最大的基础性学科竞赛，也是世界上规模最大的数学建模竞赛，各大高校对这项比赛都很重视，那么如何挑选出优秀的队员和如何将队员进行合理的组队就至关重要了。

本文将提出的问题转化为数学的模型以及合理的假设分析给出了妥帖的解决方案。

1、对于问题一我们用多元统计分析中的层次分析法首先建立了模型1.1，给各项条件指标一个权重，来计算加权函数i i ij j i iii W P L W ∑=∑===7161，αα，再求每个队员的综合水平，用Excel 整理数据，最后淘汰8、9两名队员。

然后在模型1.1的基础上建立了模型 1.2，从理论上按照层次分析法的步骤算出权重，再按模型 1.1的加权函数计算每个队员的综合水平，得出的结果也是淘汰8、9两名队员，充分的验证了模型的合理性。

2、对于问题二我们用逐项选优法和均衡模型法，由于学校参赛的目的不同给出两种模型。

我们把这个问题转化成求竞赛水平函数i j ml k ji m l k jW a W af ∑==61,,,,),(，模型2.1目的是使学校尽可能拿更高的奖项，用逐项求优法挑选竞赛水平高的队伍，重复挑选选取最优。

模型2.2目的是使学校尽可能多的获奖，也就是期望六支队伍都获奖，用均衡模型法，先选出竞赛水平最高的一组保证能够获奖，将剩下的队员均衡分配，从而竞赛水平都达到某一高度，这样六支队伍都能获奖。

综合这两种模型我们在不同的情况下做了合理的分析，认为模型2.1优于模型2.2. 3、对于问题三我们用求价值函数和仿真的方法，模型3.1是使每个教练挑选的队员的价值函数i i k q p o i i kq p o i kW d W dg ∑==613),,(3),,(3),(达到最大，同时保证他们之间相差不大，这样才能使教练相对满意。

模型3.2是用仿真的方法，通过仿真模拟出能够满足各个教练所需求的“最优”，又能使得他们所得队员差距更小，以取得使教练都尽可能满意的结果。

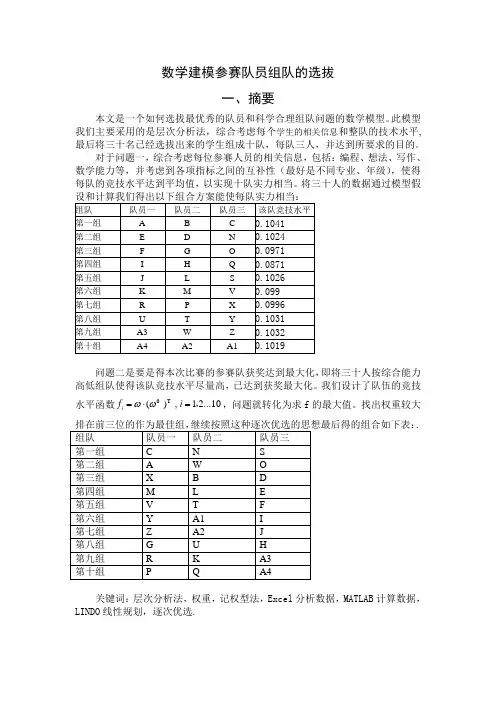
数学建模参赛队员组队的选拔一、摘要本文是一个如何选拔最优秀的队员和科学合理组队问题的数学模型。

此模型我们主要采用的是层次分析法，综合考虑每个学生的相关信息和整队的技术水平,最后将三十名已经选拔出来的学生组成十队，每队三人，并达到所要求的目的。

对于问题一，综合考虑每位参赛人员的相关信息，包括：编程、想法、写作、数学能力等，并考虑到各项指标之间的互补性（最好是不同专业、年级），使得每队的竞技水平达到平均值，以实现十队实力相当。

将三十人的数据通过模型假问题二是要是得本次比赛的参赛队获奖达到最大化，即将三十人按综合能力高低组队使得该队竞技水平尽量高，已达到获奖最大化。

我们设计了队伍的竞技水平函数0T ( ) , 12...10i f i ωω=⋅=，，问题就转化为求f 的最大值。

找出权重较大.关键词：层次分析法，权重，记权型法，Excel 分析数据，MATLAB 计算数据，LINDO 线性规划，逐次优选.二、问题重述全国大学生数学建模比赛是由教育部发起的18项大学生创新训练项目之一，目前已为广大大学生所熟悉。

目的在于激励学生学习数学的积极性，提高学生建立数学模型和运用计算机技术解决实际问题的综合能力，鼓励广大学生踊跃参加课外科技活动，开拓知识面，培养创造精神及合作意识，推动大学数学教学体系、教学内容和方法的改革。

河海大学常州校区每年都会有一定数量的学生参加此项赛事，并取得了一定的成绩。

为此，数理部每年暑期将会对学生进行培训，最后选拔出参赛的队员。

选拔条件为：思维活跃、编程能力强、熟练的写作技巧、良好团队合作意识。

附件里给出了某年的已经选拔出来的学生相关信息，包括：编程、想法、写作、数学能力等。

根据根据所给的信息，进行组队，每队三人，组队原则如下：1）尽可能地不同学院、不同性别2）如果同一学院，尽可能地不同专业3）每个队伍中，至少一个人能胜任编程、想法、写作中的一项。

根据如下要求，完成下面的问题： 1．如何组队，使得每队的实力相当； 2．如果考虑到获奖最大化，如何组队；3．数据中没有给出团队合作意识的量化数据，问，如果考虑团队合作意识这一因素，如何建立模型。

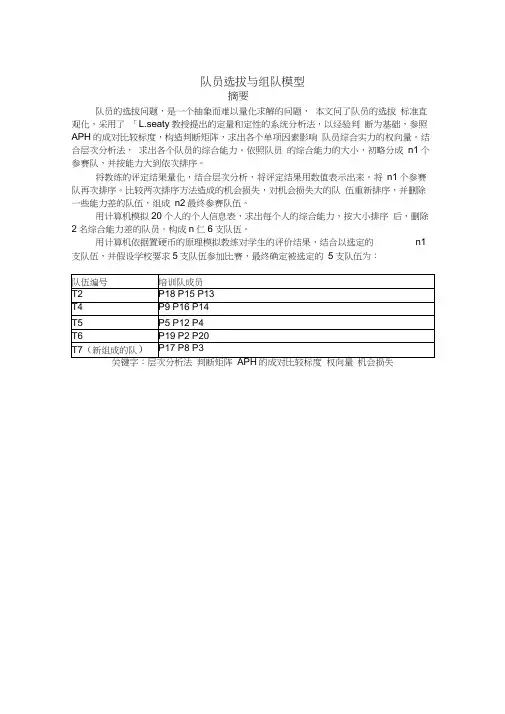
队员选拔与组队模型摘要队员的选拔问题，是一个抽象而难以量化求解的问题，本文问了队员的选拔标准直观化，采用了「L.seaty教授提出的定量和定性的系统分析法，以经验判断为基础，参照APH的成对比较标度，构造判断矩阵，求出各个单项因素影响队员综合实力的权向量。

结合层次分析法，求出各个队员的综合能力。

依照队员的综合能力的大小，初略分成n1个参赛队，并按能力大到依次排序。

将教练的评定结果量化，结合层次分析，将评定结果用数值表示出来。

将n1个参赛队再次排序。

比较两次排序方法造成的机会损失，对机会损失大的队伍重新排序，并删除一些能力差的队伍，组成n2最终参赛队伍。

用计算机模拟20个人的个人信息表，求出每个人的综合能力，按大小排序后，删除2名综合能力差的队员。

构成n仁6支队伍。

用计算机依据置硬币的原理模拟教练对学生的评价结果，结合以选定的n1支队伍，并假设学校要求5支队伍参加比赛，最终确定被选定的5支队伍为：关键字：层次分析法判断矩阵的成对比较标度权向量机会损失一. 问题重述面对每年一次的全国大学生数学建模竞赛及美国大学生数学建模竞赛, 学校需要花费较多的人力以及财力从报名的学生中选拔出优秀的学生并组成具有竞争力的参赛队, 期望获得最好的成绩.数学建模竞赛的每一个参赛队由3 名同学组成, 要求在三天的时间内完成一个实际问题的求解, 包括问题描述、问题分析、建立模型、模型求解算法设计、编写程序求得结果、模型以及算法改进、模型稳定性分析、优缺点分析，最后撰写论文等。

竞赛过程中仅允许本队队员之间讨论，并可以利用图书馆中的图书资料以及网上的正确可靠资源。

为最终组成有竞争力的参赛队, 计划分两步来挑选队员, 具体如下: 第一步依据报名表中的信息挑选出优秀的学生，并3人一组组成n1个培训队。

报名表（附件4）。

第二步对挑选出的队员进行培训。

在培训期间要经过3 至6次的模拟竞赛，m 个教练对每一个培训队的每一次竞赛都有一个综合评价和单项评价，单项评价包括写作水平、模型的正确性和简洁性、算法的正确性和复杂度、创新点共四项，评价成绩分为：优秀、优良、一般。

数学建模选拔队员问题【摘要】全国研究生数学建模竞赛是一项关系到学校和个人荣誉的比赛,因此一个参赛院校如何选拔最优秀的队员和科学合理地组队是一个亟待解决的问题。

我们建立模型解决数学建模队员选拔与组队问题。

第一，队员选择模型。

首先，我们将所给队员的七项基本条件指标划分为知识、能力、表现三类。

运用层次分析法，建立成对比较矩阵，得到三类的权重继而得到七项条件的权重。

然后采用模糊物元法,计算每位队员各项指标的联系系数，并与权重结合得到队员的联系度，依此排名,淘汰排名最后的五位队员。

第二，最佳组队模型。

首先对于某些互补性的条件指标，取三名队员的最大值作为整队指标；对于某些整体性的条件指标，取三名队员的平均值作为整队指标。

然后结合各指标权重建立竞赛水平函数，同时对每项指标进行一定约束。

最后通过Mａｔlaｂ软件计算，求得最佳组队队员。

【关键词】选拔队员与组队层次分析法模糊物元法竞赛水平函数1 引言数学建模竞赛要求以不超过三人的团队参加，其主旨为培养学生的创新意识和团队精神。

这是一项关系到学校和个人荣誉的比赛,因此一个参赛院校如何选拔最优秀的队员和科学合理地组队是一个亟待解决的问题。

目前，２01２年浙江师范大学有２6名队员准备参加竞赛,已知每位队员的平时成绩、智力水平、计算机能力、参赛经验、写作能力、协作能力、身体状况。

假设所有队员接受了同样的培训,不考虑其他随机因素的影响，我们建立数学模型解决如下问题:1．在26名队员中选择２1名优秀队员参加竞赛；2.确定一个最佳的组队方案使竞赛技术水平最高。

2 模型假设1.假设所有队员接受了同样的培训,不考虑其他随机因素的影响;假设层次分析求权重带来的主观因素影响不会有太大影响；３符号说明符号说明A、B 成对比较矩阵a表示第i个因素相对于第j个因素的比较结果ijCI 一致性检验指标数ＲI 随机一致性指标ＣＲ一致性比率ω指标权重 i M方案 j C 特征评价指标 ji x指标量值 max ji xx ｊi 的最大值 min ji xx ji 的最小值 ξ关联系数i ω各个条件指标的权重系数1,2,...,7k l mi i ia a a i =、、（）随机取三个人,,k l m 的第i 项条件的联系系数1,2,...,5i p i =（）第i 项条件联系系数的最大值 6,7i q i =（）第i 项条件联系系数的平均值f竞赛水平函数4 队员选择模型我们在选拔数学建模队员时，一个队员的能力是可以从多方面衡量的,比如计算机能力，智力水平,写作能力等。

选拔队员与组队模型李吉志 胡驿姿 胡凯摘 要该模型解决了选拔参赛队员及确定最佳组队的问题。

该问题涉及面很广，是我们身边经常会遇到的。

本文主要采用了层次分析法，综合考虑个人的指标以及整队的技术水平，最终从20名队员中选出18名优秀队员并建立了最佳组队的方案。

问题一在选拔队员时，我们全面考察了队员的七个指标，并按照相应的权重最后得出20名队员的综合排名，自然最后淘汰掉排名靠后的两名队员H 、I 。

问题二为了确定一个最佳组队，使竞赛水平达到最高，我们建立了刻画一个队的函数：0T( ) , 1,2,6i f i ωω=⋅=K ，用来表示每个队的竞赛技术水平。

本问题就可以转化为找出该函数的最大值。

为了充分考虑队员之间的互补性，我们把所有指标中权重最高的队员找出，再找出权重较高的排在前三位的（G 、L 、S ）作为最佳组队，即得到解。

问题三是要让组成的6个队的整体水平最高。

我们给出了三个模型求解，但前两种都由于计算量与程序设计较为繁琐，最终选用模型三来使问题求解。

求解思路还是沿用问题二，在问题二的基础上，再在剩下的队员里，又把所有指标中权重最高的队员找出，找出权重较高的排在前三位的队员作为一组，继续按照这种逐次选优的思想，直至找到所有的分组。

最后得到的组队方案如下：分 组 队员一队员二队员三该组水平 第一组 M D T 0.0558 第二组 P F Q 0.0539 第三组 O A R 0.0532 第四组 K B J 0.0518 第五组 E C N 0.0508关键词：层次分析法，技术水平，最优组队，逐次选优一、问题的重述在一年一度的我国和美国大学生数学建模竞赛活动中，任何一个参赛院校都会遇到如何选拔最优秀的队员和科学合理组队问题。

这是一个最实际的而且首先需要解决的数学模型问题。

现假设有20名队员准备参加竞赛，根据队员的能力和水平要选出18名优秀队员分别组成6个队，每个队3名队员去参加比赛。

选拔队员主要考虑的条件依次为有关学科成绩（平均成绩）、智力水平（反映思维能力、分析问题和解决问题能力等）、动手能力（计算机的使用和其它方面实际操作能力）、写作能力、外语能力、协作能力（团结协作能力）和其他特长。

数学建模队员的选拔-层次分析法层次分析法（Analytic Hierarchy Process，简称AHP）是一种多准则决策方法，通过构造层次结构分析问题，通过对于决策中所涉及的因素和目标进行层次分解，将问题的各部分分解成若干层次，在该层次结构中使用定量和定性的方法来描述因素之间的关联和权重。

本文将利用层次结构模型，以及层次分析法，对数学建模队员的选拔进行分析。

层次结构模型在进行数学建模队员的选拔中，影响选拔的多个因素可以构建成一个层次结构模型。

例如：在数学建模队员选拔中，可以将最终选出的队员作为最终的目标，而影响选拔的因素可以分解成以下多个因素：1.专业水平：参赛者们的数学水平、学习能力、逻辑思维等问题。

2.团队合作能力：参赛者是否适应团队合作及与人组队互动等问题。

3.沟通和表达能力：参赛者的表达能力、口头和文字沟通交流等问题。

4.个人素质：如责任感、进取心、合作精神、团队协作精神等。

层次分析法在层次分析法中，问题通常首先进行分层，使用准则、子准则和指标以及目标来描述问题，并按照这种结构构造一个具有层次结构特征的问题描述。

接着，将问题中的各个层次之间的依赖关系描述出来，并将各个准则、子准则、指标和目标的重要性大小转化为数量化的比较关系。

比较矩阵是层次分析法中的核心概念。

比较矩阵是一种用于比较各个因素之间差异的矩阵视图，在比较矩阵中，每一个单元格代表两个不同的元素之间的相对权重。

比较矩阵的各行数值之和为1。

以数学建模队员选拔的专业水平为例：在该因素层面上考虑选择队员是否有良好的数学水平、学习能力、逻辑思维；在这些因素比较中，可以进行两两比较后形成下图所示的矩阵视图。

| 比较矩阵 | 数学水平 | 学习能力 | 逻辑思维 ||--------------|----------|----------|----------|| 数学水平 | 1 | 3 | 5 || 学习能力 | 1/3 | 1 | 3 || 逻辑思维 | 1/5 |1/3 | 1 |上表中的数字代表数量级：按比例表示数据之间的重要程度或优先级，并且满足归一化性质：对于矩阵中的每一列，它们的权重比之和应为1。

数学建模论文学院：计算机与信息学院专业班级：信息与计算科学111班姓名：熊溢斌学号：3110702143题目：一年一度的全国大学生数学建模竞赛是高等院校的重要赛事。

由于竞赛场地、经费等原因，不是所有想参加竞赛的人都能被录用。

为了能够选拔出真正优秀的同学代表学校参加全国竞赛，数学建模教练组需要投入大量的精力，但是每年在参赛的时候还是有很多不如意之处：有的学生言过其实，有的队员之间合作不默契，影响了数学建模的成绩。

数学建模需要学生具有较好的数学基础和必要的数学建模知识、良好的编程能力和熟练使用数学软件的能力、较强的语言表达能力和写作能力、良好的团队合作精神，同时还要求思维敏捷，对建立数学模型有较好的悟性。

目前选拔队员主要考虑以下几个环节数学建模培训课程的签到记录；数学建模的笔试成绩，上机操作，学生个人简介，面试，老师和学生的推荐等，通过这种方式选拔出队员。

然后按照3人一组分为若干小组，为了使得小组具有较好的知识结构，一般总是将不同专业的学生安排在一起，使得每个小组至少包含一位数学基础较好的同学、计算机编程能力强的同学。

各组通过做题进行交流和磨合，合作比较好的保留，合作不好的进行调整。

下表列出了15个学生的部分信息，空白处为学生不愿意提供或未能了解的情况学生专业笔试班级排名听课次数其它情况思维敏捷机试知识面S1 数学96 2 2 A B A S2 电子信息93 1 6 过计算机三级 A B B S3 机械92 3 4 C D C S4 机械82 10 4 上过建模选修课 B B A S5 数学82 3 B C B S6 电子信息82 3 6 A B D S7 化工与材料80 7 5 C B B S8 数学79 4 考过程序员 A B A S9 电子信息78 12 4 学过MATLAB A C C S10 电子信息77 5 学过MATLAB A B B S11 化工与材料76 6 C A B S12 化工与材料74 2 A C A S13 计算机78 2 B A D S14 计算机76 5 A B A S15 计算机66 6 C B B现在需要解决以下几个问题：1．根据你们所了解的数学建模知识，选拔数学建模队员要考察学生的哪些情况？哪些素质是数学建模的关键素质，如何进行考察？2．根据上表中信息，建立建模队员选拔的数学模型，从中选出9位同学，并组成3个队，使得这三个队具有良好的知识结构。