《计量经济学》(庞浩第一版)第五章异方差性eviews上机操作
- 格式:doc
- 大小:243.00 KB
- 文档页数:10
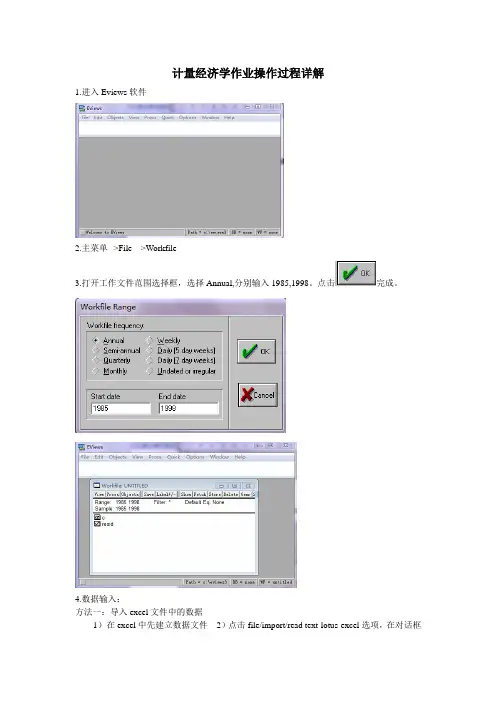
计量经济学作业操作过程详解1.进入Eviews软件2.主菜单-->File--->Workfile3.打开工作文件范围选择框,选择Annual,分别输入1985,1998。
点击完成。
4.数据输入:方法一:导入excel文件中的数据1)在excel中先建立数据文件2)点击file/import/read text-lotus-excel选项,在对话框中选择已建立的excel文件4)打开后,在新的对话框中输入想要分析的变量名称,然后点击OK即可。
此时工作文件中出现变量图标。
方法二:手工数据输入主菜单--->Quick----->Empty Group分别输入变量Y、GDP的数据。
点击obs后面的灰色格子中分别输入Y、GDP。
(方法一:一个一个输入方法二:在Excel中输入完再复制粘贴)5.主菜单---->Quick----->Estimate Equation打开估计模型对话框,输入Y C GDP ,(如上图所示,注意字母之间要有空格)点击OK键。
得出Eviews的估计结果:β(上面还要带个帽子,电脑打不出来),26.95415为1β。
其中12596.27为0第五步可以直接输入LS Y C GDP 等出结果6.一元线性回归模型的预测1)在工作文件主窗口点击procs/change workfile range(改变范围),弹出对话框,在对话框的end date栏中输入预测值的时间或序号,点击OK2)在工作文件窗口中双击解释变量文件,在变量窗口中点击edit+/-键,进入编辑模式,在变量窗口底端输入新序号的数值,再点击edit+/-键,关闭编辑模式3)再次进行估计,点击quick/estimate equation,在对话框中输入方程,注意样本范围应不包括新序号,点击OK得到估计结果4)点击结果窗口中的forecast键,产生对话框,在对话框中选择样本范围,点击OK可得预测曲线图。

Eviews应用初步教学目的:介绍Eviews计量经济软件的基本指令教学重点、难点:同时处理异方差和自相关教学时数:3教学方法:多媒体演示作业:上机练习作业题主要内容:一、打开Eviews: 开始→程序→ eviews3 → eviews3.1 →回车二、建立文件:File → new → workfile 年、季、月度数据三、输入数据:Quick → Empty group → Edit+/-四、保存数据:File → save →文件名(英文)→保存五、调用文件:File → open →workfile文件名(英文)六、显示与查看数据:选中X和Y →双击→ open group →查看、修改数据七、做散点图:选中X和Y → quick → graph → ok → scatter → option → regression line → ok八、统计分析:quick → group statistics → descriptive statistics, covariances, correlation九、回归分析:quick → estimate equation → Y C X → ok十、定义样本区间:quick → sample → 1 4→ ok十一、产生新序列:quick → generate series →公式十二、排序:Pross → sort series →序列名→升降序十三、曲线回归:log(y) c log(x)十四、处理自相关:ls y c x ar(1)根据某地区1987年~2003年人均实际消费支出(单位:元)和人均实际可支配收入(单位:元)的资料完成以下工作: 1.建立该地区人均实际消费支出对人均实际可支配收入的回归模型并进行估计和检验。
2.请用戈德费尔德—匡特检验方法判断该模型是否存在异方差性(去掉中间三年的数据),如果存在,请用加权最小二乘法消除异方差。


计量经济学第五章异⽅差性第五章异⽅差性本章教学要求:根据类型,异⽅差性是违背古典假定情况下线性回归模型建⽴的另⼀问题。
通过本章的学习应达到,掌握异⽅差的基本概念包括经济学解释,异⽅差的出现对模型的不良影响,诊断异⽅差的⽅法和修正异⽅差的若⼲⽅法。
经过学习能够处理模型中出现的异⽅差问题。
第⼀节异⽅差性的概念⼀、⼆个例⼦例1,研究我国制造业利润函数,选取销售收⼊作为解释变量,数据为1998年的⾷品年制造业、饮料制造业等28个截⾯数据(即n=28)。
数据如下表,其中y表⽰制造业利润函数,x表⽰销售收⼊(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较⼩,有的点分散幅度较⼤。
因此,这种分散幅度的⼤⼩不⼀致,可以认为是由于销售收⼊的影响,使得制造业利润偏离均值的程度发⽣变化,⽽偏离均值的程度⼤⼩的不同,就是所谓的随机误差的⽅差存在变异,即异⽅差。
如果⾮线性,则属于哪类⾮线性,从图形所反映的特征看,并不明显。
下⾯给出制造业利润对销售收⼊的回归估计。
模型的书写格式为212.03350.1044(0.6165)(12.3666)0.8547,..56.9046,152.9322213.4639,146.4905Y Y X R S E F Y s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在异⽅差性。
例2,改⾰开放以来,各地区的医疗机构都有了较快发展,不仅政府建⽴了⼀批医疗机构,还建⽴了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,⽽医疗服务需求与⼈⼝数量有关。
为了给制定医疗机构的规划提供依据,分析⽐较医疗机构与⼈⼝数量的关系,建⽴卫⽣医疗机构数与⼈⼝数的回归模型。
根据四川省2000年21个地市州医疗机构数与⼈⼝数资料对模型估计的结果如下:i iX Y 3735.50548.563?+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表⽰卫⽣医疗机构数(个),X 表⽰⼈⼝数量(万⼈)。




eviews异方差检验步骤Eviews异方差检验步骤异方差是指随着自变量的变化,因变量的方差也会发生变化。
在回归分析中,如果存在异方差,会导致回归系数的估计值不准确,从而影响模型的可靠性。
因此,进行异方差检验是非常重要的。
Eviews是一款常用的统计软件,它提供了多种方法来检验异方差。
下面我们将介绍Eviews中进行异方差检验的步骤。
步骤一:建立回归模型我们需要建立一个回归模型。
在Eviews中,可以通过“Quick”菜单中的“Estimate Equation”来建立回归模型。
在弹出的对话框中,选择因变量和自变量,并设置其他参数,如拟合方法、截距项等。
步骤二:检验异方差建立好回归模型后,我们需要进行异方差检验。
在Eviews中,可以通过“View”菜单中的“Residual Diagnostics”来进行检验。
在弹出的对话框中,选择“Heteroskedasticity Tests”选项卡,然后选择需要进行的异方差检验方法。
Eviews提供了多种异方差检验方法,包括Breusch-Pagan-Godfrey 检验、White检验、Goldfeld-Quandt检验等。
这些方法的原理和适用条件不同,需要根据具体情况选择合适的方法。
步骤三:解释检验结果进行异方差检验后,Eviews会输出检验结果。
通常包括检验统计量、p值等信息。
如果p值小于显著性水平(通常为0.05),则可以拒绝原假设,认为存在异方差。
如果检验结果显示存在异方差,我们需要对模型进行修正。
常用的方法包括使用异方差稳健标准误、进行加权最小二乘回归等。
总结Eviews提供了多种方法来检验异方差,包括Breusch-Pagan-Godfrey检验、White检验、Goldfeld-Quandt检验等。
进行异方差检验后,需要根据检验结果对模型进行修正,以提高模型的可靠性。

计量经济学(课程)上机实验指导书实验一 : Eviews软件基本操作和一元回归模型1、实验目的:1)、了解Eviews软件的特点;2)、掌握Eviews软件的启动与退出;3)、了解Eviews软件工作窗口的组成4)、掌握Eviews软件的基本操作和使用范围。
2、实验内容:1)练习Eviews软件的基本操作;2)学会利用Eviews软件的五大工具即工作文件、序列、数组、图形和方程进行经济计量分析;3以我国税收预测模型为例,建立工作文件;输入数据;图形分析;估计线性回归模型;模型比较,根据判定系数、残差图等进行综合分析。
3、预习要求及参考书目1)潘省初:《计量经济学》,中国人民大学出版社,。
2)赵卫亚:《计量经济学教程》,上海财经大学出版社,。
3)M.伍徳里奇:《计量经济学导论》,中国人民大学出版社,4、实验步骤:1)启动Eviews软件,熟悉Eviews软件的工作窗口;2)根据窗口文件提示,输入我国税收数据(见参考书2)P311);3)进行数据处理和分析;4)总结Eviews软件中的简单函数、描述统计函数和回归统计函数的使用方法和程序。
5、实验报告要求:按规定内容完成。
实验二 :Eviews的应用-多元回归分析1、实验目的:1)、重点掌握Eviews软件的多元回归分析方法;2)利用Eviews软件对回归结果进行验证。
2、实验内容:1)练习Eviews软件的基本操作程序和和各种命令文件代码;2)建立我国国有独立核算工业企业生存函数,然后建立多元线性回归模型;比较、选择最佳模型。
3)对相关数据数据进行回归分析和结果检验。
3、预习要求及参考书目1)潘省初:《计量经济学》,中国人民大学出版社,。
2)赵卫亚:《计量经济学教程》,上海财经大学出版社,。
3)M.伍徳里奇:《计量经济学导论》,中国人民大学出版社,4、实验步骤:1)在Windows窗口下启动Eviews软件;2)建立我国国有独立核算工业企业生存函数,然后建立多元线性回归模型;比较、选择最佳模型。

异方差的eviews操作图3-1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图3-2 我国制造业销售利润回归模型残差分布图3-2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
2、Goldfeld-Quant检验⑴将样本安解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3-3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3-3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图3-4),其残差平方和为63769.67。
SMPL 19 28 LS Y C X图3-4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性3、White 检验⑴建立回归模型:LS Y C X ,回归结果如图3-5。
图3-5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图3-6。
图3-6 White 检验结果其中F 值为辅助回归模型的F 统计量值。
取显著水平05.0=α,由于2704.699.5)2(2205.0=<=nR χ,所以存在异方差性。
实验一 EViews软件的基本操作【实验目的】了解EViews软件的基本操作对象,掌握软件的基本操作。
【实验内容】一、EViews软件的安装;二、数据的输入、编辑及序列生成;三、图形分析及描述统计分析;四、数据文件的存贮、调用及转换。
实验内容中后三步以表1-1所列出的税收收入和国内生产总值的统计资料为例进行操作。
表1-1 我国税收及GDP统计资料单资料来源:《中国统计年鉴1999》【实验步骤】一、安装EViews软件㈠EViews对系统环境的要求⒈一台386、486奔腾或其他芯片的计算机,运行Windows3.1、Windows9X、Windows2000、WindowsNT或WindowsXP操作系统;⒉至少4MB内存;⒊VGA、Super VGA显示器;⒋鼠标、轨迹球或写字板;⒌至少10MB以上的硬盘空间。
㈡安装步骤⒈点击“网上邻居”,进入服务器;⒉在服务器上查找“计量经济软件”文件夹,双击其中的setup.exe,会出现如图1-1所示的安装界面,直接点击next按钮即可继续安装;⒊指定安装EViews软件的目录(默认为C:\EViews3,如图1-2所示),点击OK按钮后,一直点击next按钮即可;⒋安装完毕之后,将EViews的启动设置成桌面快捷方式。
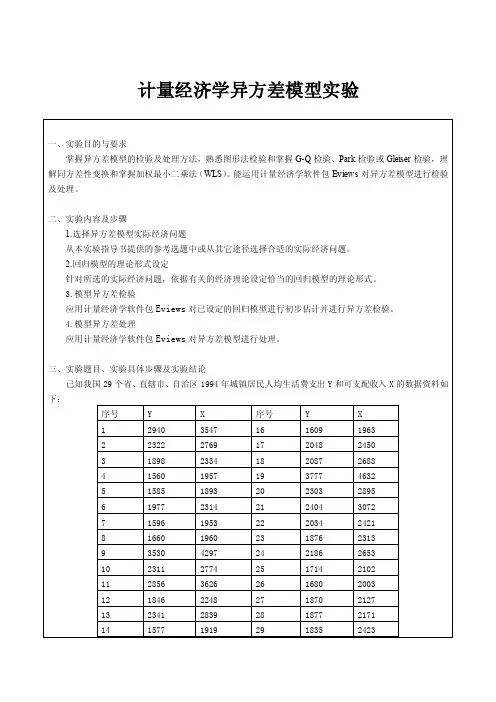
图1-1 安装界面1图1-2 安装界面2二、数据的输入、编辑及序列生成㈠创建工作文件⒈菜单方式启动EViews软件之后,进入EViews主窗口(如图1-3所示)。
标题栏菜单栏命令窗口工作区域状态栏图1-3 EViews主窗口在主菜单上依次点击,即选择新建对象的类型为工作文件,将弹出一个对话框(如图1-4所示),由用户选择数据的时间频率(frequency)、起始期和终止期。
图1-4 工作文件对话框其中, Annual——年度 Monthly——月度Semi-annual——半年 Weekly——周Quarterly——季度 Daily——日Undated or irregular——非时序数据选择时间频率为Annual(年度),再分别点击起始期栏(Start date)和终止期栏(End date),输入相应的日前1985和1998。
EViews计量经济学实验报告异⽅差的诊断及修正姓名学号实验题⽬异⽅差的诊断与修正⼀、实验⽬的与要求:要求⽬的:1、⽤图⽰法初步判断是否存在异⽅差,再⽤White检验异⽅差;2、⽤加权最⼩⼆乘法修正异⽅差。
估计结果为: iY ? = 12.03564 + 0.104393i X (19.51779) (0.008441) t=(0.616650)(12.36670)2R =0.854696 R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下,销售收⼊每增长1元,销售利润平均增长0.104393元。
2R =0.854696 , 拟合程度较好。
在给定 =0.0时,t=12.36670 > )26(025.0t =2.056 ,拒绝原假设,说明销售收⼊对销售利润有显著性影响。
F=152.9353 > )6,21(F 05.0= 4.23 ,表明⽅程整体显著。
(三)检验模型的异⽅差※(⼀)图形法6、判断由图3可以看出,被解释变量Y 随着解释变量X 的增⼤⽽逐渐分散,离散程度越来越⼤;同样,由图4可以看出,残差平⽅2 i e 对解释变量X 的散点图主要分布在图形中的下三⾓部分,⼤致看出残差平⽅2i e 随i X 的变动呈增⼤趋势。
因此,模型很可能存在异⽅差。
但是否确实存在异⽅差还应该通过更近⼀步的检验。
※(⼆)White 检验White 检验结果White Heteroskedasticity Test:F-statistic3.607218 Probability 0.042036 Obs*R-squared6.270612 Probability0.043486Test Equation:t 界值5.002χ(2)=5.99147。
⽐较计算的2χ统计量与临界值,因为n 2R = 6.270612 > 5.002χ(2)=5.99147 ,所以拒绝原假设,不拒绝备择假设,这表明模型存在异⽅差。
Eviews 主要操作步骤一、启动软件包 ( 双击“Eviews ”,进入Eviews 主页)二、创建工作文件(点击“File/New/Workfile/Ok ”)出现“Workfile Range ”,目的:1、选择数据频率(类型):Annual (年度)Quartely (季度)┆Undated or irrequar (未注明日期或不规则的)2、确定Start date 和End date (如1980 1999或1 18 /ok )。
出现“Workfile 对话框(子窗口)”中已有两个变量:c-----常数项resid----模型将产生的残差项三、输入(编辑)数据:法1:在命令框键入:“data y x ”( 一元)或“data y 1x 2x …”(多元)/回车;出现数据编辑框,按顺序键入数据/存盘(或最小化)。
法2:用鼠标单击“Quick ”,在出现的下拉菜单中单击“Empty Group ”, 出现Group 窗口。
数据表第一序列取名y ,键入y 的数据;再将数据表第二序列取名x ,键入x 的数据;…/存盘(或最小化)。
出现的对话框中有四个(一元)或五个及五个以上的(多元)变量:c-----常数项resid----将产生的残差x----解释(自)变量y----被解释(因)变量注:存盘点“File/save”,删除原文件名,输入“自命名”/ok。
注:读取(数)点“File/open”,点自命名文件/ok。
注:如数据资料已经作为Eviews的永久工作文件存盘,则二、三步省去,用File/open命令打开文件即可。
第一章简单线性回归模型;第二章多元线性回归模型一、回归分析(用OLS估计未知参数)法1:1、点击“Quick/Estimate E quation”;2、在出现的估计对话框中,键入y c x/ok法2、在命令框键入LS y c x或LS y c 1x 2x/回车。
注:在E quation框中,点击Resids,可以出现Residual、Actual、Fitted的图形。
计量经济学实验指导系部:基础部专业:计算与信息科学教师:仓定帮I.实验一多元线性回归模型 (3)II.实验二异方差的检验与处理 (16)III.实验三序列相关的检验与处理 (24)IV.实验四多重共线性的检验与处理 (32)V.实验五虚拟变量模型 (39)VI.实验六分布滞后模型 (45)VII.实验七联立方程模型 (51)VIII.实验八时间序列模型分析 (58)IX.实验九V AR模型的建立与分析 (77)A. ADF检验 (78)B. VAR模型的建立 (79)C. 协整检验 (80)D. GRANGER因果检验 (81)E. 脉冲响应分析 (81)实验内容注:必做实验课堂时间完成,选做实验由学生课后选择时间完成。
每次实验后学生上交实验分析结果。
I.实验一多元线性回归模型【实验目的】通过本实验,了解Eviews软件,熟悉软件建立工作文件,文件窗口操作,数据输入与处理等基本操作。
掌握多元线性回归模型的估计方法,学会用Eiews 软件进行多元回归分析。
通过本实验使得学生能够根据所学知识,对实际经济问题进行分析,建立计量模型,利用Eiews软件进行数据分析,并能够对输出结果进行解释说明。
【实验内容及步骤】本实验选用美国金属行业主要的27家企业相关数据,如下表,其中被解释变量Y表示产出,解释变量L表示劳动力投入,K表示资本投入。
试建立三者之间的回归关系。
7 2427.89 452 3069.91 21 5159.31 835 5206.368 4257.46 714 5585.01 22 3378.4 284 3288.729 1625.19 320 1618.75 23 592.85 150 357.3210 1272.05 253 1562.08 24 1601.98 259 2031.9311 1004.45 236 662.04 25 2065.85 497 2492.9812 598.87 140 875.37 26 2293.87 275 1711.7413 853.1 154 1696.98 27 745.67 134 768.5914 1165.63 240 1078.79【实验内容及步骤】1.数据的输入STEP1:双击桌面上Eviews快捷图标,打开Eviews,如图1.图1STEP2:点击Eviews主画面顶部按钮file/new/Workfile ,如图2,弹出workfile create对话框如图3。
第五课序列相关与异方差模型的处理5.1序列相关模型一、首先,结合案例数据(5_1_1)研究天津市城镇居民人均消费与人均可支配收入的关系,分析一阶线性相关存在时模型的检验与处理。
(1)案例数据:改革开放以来,天津市城镇居民人均消费性支出(CONSUM),人均可支配收入(INCOME)以及消费价格指数(PRICE)数据(1978—2000年)见下表。
(数据来源:张晓峒,《计量经济学基础》,P152,例6.1)(2)散点图考虑到价格指数的影响,将CONSUM和INCOME各自除以价格指数,形成被解释变量和解释变量:CONSUM/PRICE和INCOME/PRICE,并作散点图如下,分析散点图,CONSUM/PRICE和INCOME/PRICE呈现线性相关。
(3)回归结果,Eviews输出结果报告,得到回归方程CONSUM/PRICE = 111.4400081 + 0.7118287831*INCOME/PRICEDependent Variable: CONSUM/PRICEVariable Coefficient Std. Error t-Statistic Prob.C 111.4400 17.05592 6.533804 0.0000INCOME/PRICE 0.711829 0.016899 42.12221 0.0000Adjusted R-squared 0.987746 S.D. dependent var 296.7204S.E. of regression 32.84676 Akaike info criterion 9.904525Sum squared resid 22657.10 Schwarz criterion 10.00326Log likelihood -111.9020 F-statistic 1774.281Durbin-Watson stat 0.598571 Prob(F-statistic) 0.00000005.0=α水平上,T=23条件下,k=1时,临界值Dl=1.26,由结果可知,DW=0.59<Dl,因此原模型中存在序列正相关。
第五章异方差性案例分析一、问题的提出和模型设定为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束,则理论模型设定为:ii i u X b b Y ++=21其中i Y 表示卫生医疗机构数,i X 表示人口数。
数据搜集四川省2000年各地区医疗机构数与人口数地区人口数(万人) 医疗机构数(个)Y地区人口数(万人) 医疗机构数(个)YXX成都 1013.3 6304 眉山 339.9 827 自贡 315 911 宜宾 508.5 1530 攀枝花 103 934 广安 438.6 1589 泸州 463.7 1297 达州 620.1 2403 德阳 379.3 1085 雅安 149.8 866 绵阳 518.4 1616 巴中 346.7 1223 广元 302.6 1021 资阳 488.4 1361 遂宁 371 1375 阿坝 82.9 536 内江 419.9 1212 甘孜 88.9 594 乐山 345.9 1132 凉山 402.41471 南充709.24064二、参数估计Eviews上机具体操作:利用eviews3.0进行分析第一步:建立数据1新建工作文档:file-new-workfile,在打开的workfile range对话框中的workfile frequency 中选择undated or irregular,start observation输入1,end observation输入21,点击ok。
2输入数据(先是data y x2 x3······然后是将excel中的数据复制过来即可)并保存本题在命令窗口输入data y x,并点击name命名为GROUP01.第二步:做回归1最小二乘估计(ls y c x2 x3 ······)本题在命令窗口输入ls y c x ,并点击name命名为EQ01.Dependent Variable: YMethod: Least SquaresDate: 12/04/12 Time: 12:29Sample: 1 21Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -562.9074 291.5642 -1.930646 0.0686X 5.372828 0.644239 8.339811 0.0000R-squared 0.785438 Mean dependent var 1588.143Adjusted R-squared 0.774145 S.D. dependent var 1310.975S.E. of regression 623.0301 Akaike info criterion 15.79746Sum squared resid 7375164. Schwarz criterion 15.89694Log likelihood -163.8733 F-statistic 69.55245Durbin-Watson stat 1.947198 Prob(F-statistic) 0.000000Y= -562.9073782 + 5.37282842i Xi(-1.930646)(8.339811)2R=0.785438 F=69.55245 df=19三、检验模型的异方差图形法1生成残差平方序列2ei在得到上述回归结果后,用生成命令生成序列2e,记为e2 。
生成过i程如下,先按路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入e2=(resid)∧2并点“OK”即可。
2绘制2e对Xt的散点图。
按住ctrl同时选择变量名X与te2 ,(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),进入数据列表,再按路径view/ graph/scatter/simple scatter,可得散点图,见下图:0500000100000015000002000000250000020040060080010001200XE 2判断由上图可以看出,残差平方2i e 对解释变量i X 的散点图主要分布在图形中的下三角部分,大致看出残差平方2i e 随 i X 的变动呈增大的趋势,因此,模型很可能存在异方差。
但是否确实存在异方差还应通过更进一步的检验。
Goldfeld-Guanadt 检验(1)对变量取值排序(按递增或递减)。
在Procs 菜单里选Sort Current Page/Sort Workfile Series 命令,出现排序对话框,如果以递增型排序,选“Ascenging”,如果以递减型排序,则应选“Descending”, 键入 X ,点ok 。
本例选递增型排序,这时变量Y 与 X 将以 X 按递增型排序。
(2)构造子样本区间,建立回归模型。
在本例中,样本容量n=21,删除中间1/4的观测值,即大约5个观测值,余下部分平分得两个样本区间:1—8和14—21,它们的样本个数均是8个,即 n 1=n 2=8 在工作文件窗口中点击sample ,在弹出的对话框中输入“1 8”,将样本期改为1-8,然后做回归并命名为eq02,得Dependent Variable: YMethod: Least SquaresDate: 12/04/12 Time: 13:06Sample: 1 8Included observations: 8Variable Coefficient Std. Error t-Statistic Prob.C 598.2525 119.2922 5.015018 0.0024X 1.177650 0.490187 2.402452 0.0531R-squared 0.490306 Mean dependent var 852.6250Adjusted R-squared 0.405357 S.D. dependent var 201.5667S.E. of regression 155.4343 Akaike info criterion 13.14264Sum squared resid 144958.9 Schwarz criterion 13.16250Log likelihood -50.57056 F-statistic 5.771775Durbin-Watson stat 1.656269 Prob(F-statistic) 0.053117同理在工作文件窗口中点击sample,在弹出的对话框中输入“14 21”,将样本期改为14-21,然后做回归并命名为eq03,得Dependent Variable: YMethod: Least SquaresDate: 12/04/12 Time: 13:09Sample: 14 21Included observations: 8Variable Coefficient Std. Error t-Statistic Prob.C -2940.426 430.7787 -6.825839 0.0005X 9.177641 0.693419 13.23534 0.0000R-squared 0.966883 Mean dependent var 2520.500Adjusted R-squared 0.961363 S.D. dependent var 1781.627S.E. of regression 350.2011 Akaike info criterion 14.76721Sum squared resid 735844.7 Schwarz criterion 14.78707Log likelihood -57.06884 F-statistic 175.1744Durbin-Watson stat 1.815102 Prob(F-statistic) 0.000011(3)求F 统计量值基于上面的两个回归中残差平方和的数据,即Sum squared resid 的值。
由eq02计算得到的残差平方和为21ie ∑= 144958.9 ,由eq03计算得到的残差平方和为22ie ∑=735844.7。
根据Goldfeld-Quanadt 检验,F 统计量为===∑∑144958.9735844.72122iiee F 5.066(4)判断,在α=0.05下,F 0.05(6,6)=4.28,因为F >F 0.05(6,6)=4.28,所以拒绝原假设,表明模型确实存在异方差。
White 检验在eq01估计结果后,按路径view/residual tests/white heteroskedasticity (no cross terms or cross terms ),进入White 检验。
根据White 检验中辅助函数的构造,最后一项为变量的交叉乘积项,因为本例为一元函数,故无交叉乘积项,因此应选no cross terms ,则辅助函数为: t t t t v x x +++=22102ααασ经估计出现White 检验结果,见下表。
White Heteroskedasticity Test:F-statistic 55.61118 Probability 0.000000 Obs*R-squared18.07481 Probability0.000119Test Equation:Dependent Variable: RESID^2 Method: Least Squares Date: 12/04/12 Time: 13:29 Sample: 1 21Included observations: 21VariableCoefficientStd. Error t-Statistic Prob. C 823375.5 130273.4 6.320365 0.0000 X -3605.578 553.5894 -6.513091 0.0000 X^2 4.7423870.532352 8.908366 0.0000 R-squared0.860705 Mean dependent var 351198.3 Adjusted R-squared 0.845228 S.D. dependent var 454261.0 S.E. of regression 178711.1 Akaike info criterion 27.15649 Sum squared resid 5.75E+11 Schwarz criterion 27.30571 Log likelihood -282.1432 F-statistic 55.61118 Durbin-Watson stat1.687985 Prob(F-statistic)0.000000从上面可以看出=2nR 18.07481,由White 检验知,在α=0.05下,查分布表得临界值9915.5)2(205.0=χ,同时X 和X 2的t 检验也显著。