两位数直加直减

两位数加减教案这是一份针对两位数加减运算的教案，旨在帮助学生提高他们的计算能力和数学思维。

教案将分为三个部分：教学目标、教学活动和评估方法。

教学目标：1. 学生能够理解和掌握两位数加法和减法运算的概念和方法。

2. 学生能够熟练地进行两位数加法和减法运算。

3. 学生能够应用所学的知识解决实际问题。

教学活动：1. 导入：通过一些趣味的问题和例子引发学生对两位数加减运算的兴趣和思考，例如：小明有25元，他买了一本书花了15元，那他还剩下多少钱？如果他还想再买一本书，他还需要多少钱？2. 概念讲解：通过教师的讲解和示范，向学生介绍两位数加法和减法运算的概念和方法。

包括实际操作和算式的表示方法。

3. 练习：给学生一些两位数加减运算的练习题，让他们进行计算。

教师可以根据学生的掌握情况调整难易程度。

同时，鼓励学生互相交流和讨论解题方法。

4. 应用：设计一些与现实生活相关的问题，让学生将所学的两位数加减运算应用于解决实际问题。

例如：小红有58颗糖果，她送给了朋友12颗，还剩下多少颗？5. 总结：通过课堂讨论和总结，引导学生总结两位数加减运算的规律和方法，并与他们之前所学的数学知识进行联系。

评估方法：1. 课堂练习：通过课堂上的练习题来检查学生对两位数加减运算的掌握程度。

2. 交流讨论：通过鼓励学生之间的互相交流和讨论，评估他们对所学知识的理解和应用能力。

3. 应用问题解答：通过学生对实际问题的解答来评估他们将所学的知识应用于解决问题的能力。

通过这份教案，学生将能够系统地学习和掌握两位数加减运算的方法，提高他们的计算能力和数学思维。

同时，通过应用问题的训练，他们将能够更好地将所学的知识应用于实际生活中，培养他们的问题解决能力和创新思维。

教师可以根据学生的不同情况进行差异化教学，给予他们适当的挑战，促进他们的个性化发展。

两位数减两位数的口算数学教案：口算两位数加、减两位数课题：口算两位数加、减两位数教学目标：1. 学生能够进行口算两位数加、减两位数的运算。

2. 学生能够运用口算技巧快速准确地计算结果。

3. 学生能够运用所学的口算技巧解决实际问题。

教学准备：1. 准备好两位数加、减法的口算题目。

2. 准备白板、黑板、彩色粉笔或白板笔。

教学步骤：步骤一：复习复习一下两位数的加法和减法口算技巧，例如：37 + 24 = （将37拆分成30+7，24拆分成20+4，然后相加得到50+11=61）89 - 42 = （将89拆分成80+9，42拆分成40+2，然后相减得到40+67=67）通过操练几道题目，让学生再次熟悉口算技巧。

步骤二：讲解口算两位数加法的技巧1. 将两位数加法题目拆分成基础的单位加法。

例如：56 + 24 = （将56拆分成50+6，24拆分成20+4，然后相加得到70+10=80）2. 讲解进位的概念。

当个位上的和超过10时，需要向十位进位一位。

例子：58 + 47 = （将58拆分成50+8，47拆分成40+7，然后相加得到90+15=105）步骤三：操练口算两位数加法让学生通过操练口算两位数加法的题目，巩固口算技巧。

步骤四：讲解口算两位数减法的技巧1. 将两位数减法题目拆分成基础的单位减法。

例如：79 - 36 = （将79拆分成70+9，36拆分成30+6，然后相减得到40+3=43）2. 当十位的减数大于被减数的十位，需要向百位借位一位。

例子：57 - 68 = （将57拆分成50+7，68拆分成60+8，然后相减得到(-10) + (-1) = -11）在解决这类题目时，让学生了解减法的结果可以是负数。

步骤五：操练口算两位数减法让学生通过操练口算两位数减法的题目，巩固口算技巧。

步骤六：综合练习和应用给学生一些综合练习题目，让他们综合运用口算技巧进行计算。

例如：78 + 24 = （将78拆分成70+8，24拆分成20+4，然后相加得到90+12=102）教学提示：1. 在讲解口算技巧时，可以通过具体示例进行说明，让学生更好地理解和掌握。

数学二年级二位数加减法数学是一门基础学科，也是我们学习过程中必不可少的一部分。

在数学学习过程中，我们会遇到各种各样的题目和问题，而其中二位数加减法就是我们初学数学时需要重点掌握的内容之一。

今天，我们就来详细了解一下二位数加减法的方法和技巧。

一、二位数加法在二位数加法中，我们需要将两个二位数进行相加，并注意进位的规则。

具体的步骤如下：1. 将两个二位数竖式排列，十位对齐，个位对齐。

例如： 35+ 47--------2. 从个位开始逐列相加。

首先将个位上的数字相加，得到个位的和。

这里的个位分别是5和7，它们的和是5+7=12，所以将2写在个位的下方，然后将十位上的数字相加。

35+ 47------23. 再将十位上的数字相加，并加上可能的进位。

这里的十位分别是3和4，它们的和是3+4=7。

由于没有进位，所以直接将7写在十位的下方。

35+ 47------724. 最后得到的结果就是两个二位数的和。

所以35+47=72。

二、二位数减法在二位数减法中，我们需要将两个二位数进行相减，并注意借位的规则。

具体的步骤如下：1. 将两个二位数竖式排列，十位对齐，个位对齐。

例如： 68- 27--------2. 从个位开始逐列相减。

首先将个位上的数字相减，得到个位的差。

这里的个位分别是8和7，它们的差是8-7=1，所以将1写在个位的下方，然后将十位上的数字相减。

68- 27------13. 再将十位上的数字相减，并考虑借位。

这里的十位分别是6和2，由于6大于2，所以可以直接相减，6-2=4。

将4写在十位的下方。

68- 27------414. 最后得到的结果就是两个二位数的差。

所以68-27=41。

总结起来，掌握二位数加减法的方法主要包括竖式排列、逐列相加或相减、进位和借位的处理。

通过不断的练习和巩固，我们可以更好地掌握这些技巧，并在解决实际问题时能够更准确地计算。

希望同学们能够认真对待数学学习，加强对二位数加减法的理解和应用能力，为今后的数学学习打下坚实的基础。

两位数加减两位数的方法1. 直接加法：将两位数的个位数与十位数与加数的个位数与十位数分别相加。

如果个位数的和大于等于10，将进位的十位数加到十位数上，得到最终的和。

2. 直接减法：将被减数的个位数与十位数与减数的个位数与十位数分别相减。

如果被减数的个位数小于减数的个位数，需要向十位数先借1，然后再进行相减。

3. 进位加法：将两位数的个位数与十位数与加数的个位数与十位数分别相加。

如果个位数的和大于等于10，将进位的十位数加到十位数上，同时将个位数减去10。

4. 借位减法：将被减数的个位数与十位数与减数的个位数与十位数比较。

如果被减数的个位数小于减数的个位数，需要向十位数借1，并将被减数的个位数加上10，然后再进行相减。

5. 拆分加法：将两位数的个位数与十位数与加数的个位数与十位数分别相加，拆分成四个加法运算。

首先相加个位数，如果和大于等于10，则进位到十位数，然后将个位数和进位的十位数相加得到个位数的和。

最后将十位数相加。

6. 拆分减法：将被减数的个位数与十位数与减数的个位数与十位数分别相减，拆分成四个减法运算。

首先相减个位数，如果被减数的个位数小于减数的个位数，则向十位数借位，并将被减数的个位数加上10，然后相减得到个位数的差。

最后相减十位数。

7. 扩展进位加法：将两位数的个位数与十位数与加数的个位数与十位数分别相加，如果个位数的和大于等于10，将进位的十位数加到十位数上。

然后将个位数的和再与加数的十位数相加，如果再次大于等于10，将进位的百位数加到百位数上。

8. 扩展借位减法：将被减数的个位数与十位数与减数的个位数与十位数比较，如果被减数的个位数小于减数的个位数，则向十位数借位，并将被减数的个位数加上10。

然后将个位数和十位数的差再与减数的十位数相减，如果差小于减数的十位数，则再次向百位数借位并将差加上10。

9. 拆分扩展进位加法：将两位数的个位数与十位数与加数的个位数与十位数分别相加，拆分成四个加法运算。

九归口诀共61句：一归(用1除)：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九。

二归(用2除)：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五。

三归(用3除)：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二。

四归(用4除)：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二。

五归(用5除)：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八。

六归(用6除)：逢六进一，逢十二进二，六三添作五，六一下加四，六二三余二，六四六余四，六五八余二。

七归(用7除)：逢七进一，逢十四进二，七一下加三，七二下加六，七三四余二，七四五余五，七五七余一，七六八余四。

八归(用8除)：逢八进一，八四添作五，八一下加二，八二下加四，八三下加六，八五六余二，八六七余四，八七八余六。

九归(用9除)：逢九进一，九一下加一，九二下加二，九三下加三，九四下加四，九五下加五，九六下加六，九七下加七，九八下加八。

退商口诀共9句：无除退一下还一，无除退一下还二，无除退一下还三无除退一下还四，无除退一下还五，无除退一下还六无除退一下还七，无除退一下还八，无除退一下还九商九口诀共9句：见一无除作九一，见二无除作九二，见三无除作九三见四无除作九四，见五无除作九五，见六无除作九六见七无除作九七，见八无除作九八，见九无除作九九除数是一位数的除法叫“单归”;除数是两位或两位以上的除法叫“归除”，除数的首位叫“归”，以下各位叫“除”。

如，除数是534的归除，叫“五归三四除”，即用五归口诀求商后，再用34除。

幼儿珠心算口诀加一请拨双下九，我们都是好朋友；加二请拨双下八，开心时候笑哈哈；加三请拨双下七，有时也会生生气；加四请拨双下六，快乐时候蹦又跳。

减一请拨双上九，唱歌要学百灵鸟；减二请拨双上八，做事不要太拖拉；减三请拨双上七，排队做操要整齐；减四请拨双上六，早上不要睡懒觉。

从上表的"加"来看共26个动珠码，"减"只是反向拨珠，加与减是一上一下和一去一回的还原关系，是一种动作相对形态。

《两位数加减两位数》100以内的加法和减法contents•两位数的加法•两位数的减法目录•100以内的加法和减法•练习和挑战两位数加法是指将两个两位数相加，得到一个和（也是一个两位数）。

例如：32+46=78。

两位数加法的定义同位相加。

即个位数相加，十位数相加。

规则二满十进一。

即个位数相加满10，向十位数进1。

特殊情况一两个两位数的十位数相同时，可以直接相加。

特殊情况二两个两位数的十位数不相同时，需要先调整十位数，再进行相加。

从一个两位数中减去另一个两位数的运算。

两位数减法被减去的两位数。

被减数从被减数中减去的两位数。

减数减法的结果，也是一个两位数。

差两位数减法的定义从被减数中减去减数。

先从被减数的个位数开始减，再从十位数开始减。

如果十位数相减出现0，则从1开始减；如果个位数相减出现0，则从10开始减。

如果被减数的个位数小于减数的个位数，则需要从被减数的十位数中借1，再与个位数相加后再减。

如果被减数的十位数小于减数的十位数，则需要从被减数的百位数中借1，再与十位数相加后再减。

掌握100以内的加法和减法，是学习更高级数学的基础。

基础数学技能日常生活需要提升思维能力在日常生活中，很多时候需要用到100以内的加法和减法，比如购物、计算时间等。

学习100以内的加法和减法，有助于提升逻辑思维和推理能力。

030201100以内加法和减法的重要性01加法技巧02凑十法：将一个数拆成两个数，一个数与另一个数凑成10，再与另一个数相加。

03计数法：用手指或物品计数，帮助理解加法的概念。

04减法技巧05平分法：将一个数分成两个数，减去另一个数再平分得到结果。

06数轴法：用数轴表示数字关系，帮助理解减法的概念。

如何进行100以内的加法和减法在购物时，使用100以内的加法和减法计算价格和找零。

购物计算在计算时间时，使用100以内的加法和减法计算小时、分钟和秒。

时间计算在数据分析中，使用100以内的加法和减法计算平均数、中位数和众数等统计指标。

一年级下册数学教案-4.1 两位数加、减两位数（不进位加法）
▏北京版
教学目标
1.能够用不进位的方法，解决没有进位的两位数的加法；
2.能够正确地对两位数进行加、减操作；
3.能够运用所学知识自主解决相关题目。

教学重点
1.不进位的两位数加法；
2.两位数的加、减运算。

教学难点
1.理解不进位加法的概念；
2.运用所学知识解决相关问题。

教学过程
导入
1.师生问候；
2.教师讲解本节课的学习内容：两位数的加、减法；
3.教师出示两位数加法和减法的算式，让学生尝试计算。

理解不进位加法
1.教师出示两个两位数的数字，用不进位加法的方法让学生解决；
2.引导学生分析不进位加法的规律，理解不进位加法的概念。

两位数的加法
1.教师出示两个两位数之间的加法算式，讲解该算式的步骤；
2.让学生独立尝试完成相关的题目，教师巡视并给予指导。

两位数的减法
1.教师出示两个两位数之间的减法算式，讲解该算式的步骤；
2.让学生独立尝试完成相关的题目，教师巡视并给予指导。

练习
1.教师出示大量的两位数加减法的算式，让学生独立尝试计算；
2.让学生交换算式并互相检查答案，教师指导学生改正错误。

总结
1.教师总结本节课的学习内容和重点；
2.教师与学生一起回顾本节课的收获；
3.教师布置作业并提示注意事项。

总结
本节课主要讲解了两位数的加、减法，学生可以通过本节课的学习，掌握不进位加法的概念，并能够正确地完成两位数的加、减运算。

在课后的作业中，学生还需要加强练习，并熟练掌握相关知识。

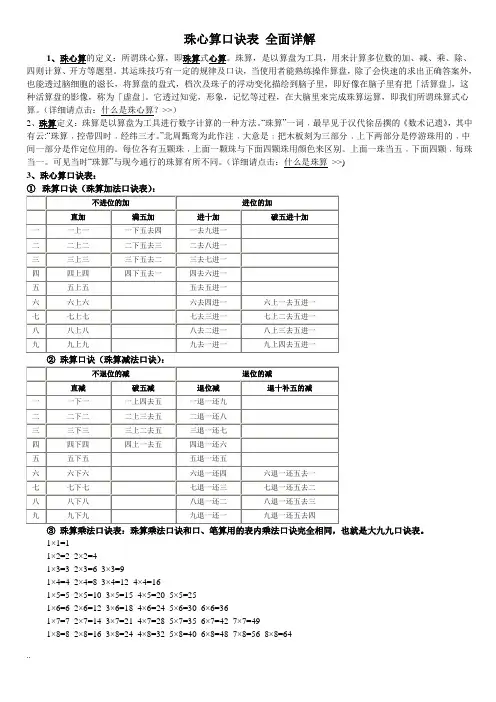
1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81④珠心算口诀表（除法口诀表：珠算除法有归除法和商除法两种）归除法用口诀进行计算，有九归口诀，退商口诀和商九口诀。

九归口诀共61句：一归(用1除)：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九。

二归(用2除)：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五。

三归(用3除)：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二。

四归(用4除)：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二。

五归(用5除)：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八。

六归(用6除)：逢六进一，逢十二进二，六三添作五，六一下加四，六二三余二，六四六余四，六五八余二。

七归(用7除)：逢七进一，逢十四进二，七一下加三，七二下加六，七三四余二，七四五余五，七五七余一，七六八余四。

八归(用8除)：逢八进一，八四添作五，八一下加二，八二下加四，八三下加六，八五六余二，八六七余四，八七八余六。

九归(用9除)：逢九进一，九一下加一，九二下加二，九三下加三，九四下加四，九五下加五，九六下加六，九七下加七，九八下加八。

退商口诀共9句：无除退一下还一，无除退一下还二，无除退一下还三无除退一下还四，无除退一下还五，无除退一下还六无除退一下还七，无除退一下还八，无除退一下还九商九口诀共9句：见一无除作九一，见二无除作九二，见三无除作九三见四无除作九四，见五无除作九五，见六无除作九六见七无除作九七，见八无除作九八，见九无除作九九除数是一位数的除法叫“单归”;除数是两位或两位以上的除法叫“归除”，除数的首位叫“归”，以下各位叫“除”。

如，除数是534的归除，叫“五归三四除”，即用五归口诀求商后，再用34除。

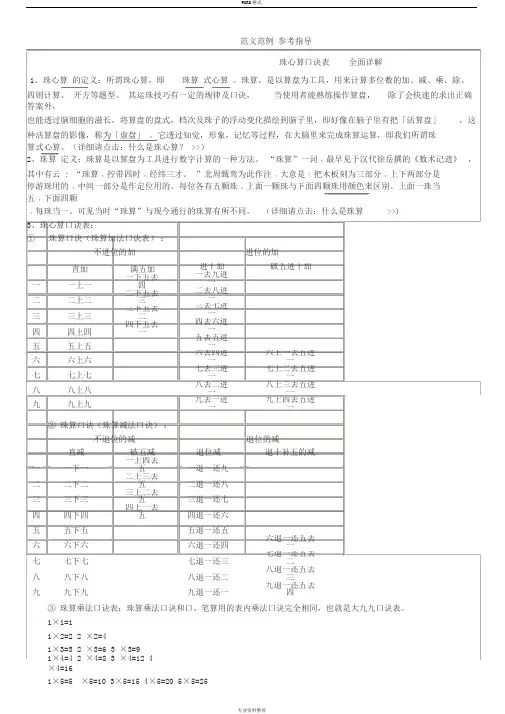
范文范例 参考指导珠心算口诀表 全面详解1、珠心算 的定义：所谓珠心算，即 珠算 式心算 。

珠算，是以算盘为工具，用来计算多位数的加、减、乘、除、四则计算、 开方等题型。

其运珠技巧有一定的规律及口诀， 当使用者能熟练操作算盘， 除了会快速的求出正确答案外， 也能透过脑细胞的滋长，将算盘的盘式，档次及珠子的浮动变化描绘到脑子里，即好像在脑子里有把「活算盘」 ，这种活算盘的影像，称为「虚盘」 。

它透过知觉，形象，记忆等过程，在大脑里来完成珠算运算，即我们所谓珠算式心算。

（详细请点击：什么是珠心算？ >>） 2、珠算 定义：珠算是以算盘为工具进行数字计算的一种方法。

“珠算”一词﹐最早见于汉代徐岳撰的《数术记遗》 ，其中有云 : “珠算﹐控带四时﹐经纬三才。

”北周甄鸾为此作注﹐大意是﹕把木板刻为三部分﹐上下两部分是停游珠用的﹐中间一部分是作定位用的。

每位各有五颗珠﹐上面一颗珠与下面四颗珠用颜色来区别。

上面一珠当五﹐下面四颗 ﹐每珠当一。

可见当时“珠算”与现今通行的珠算有所不同。

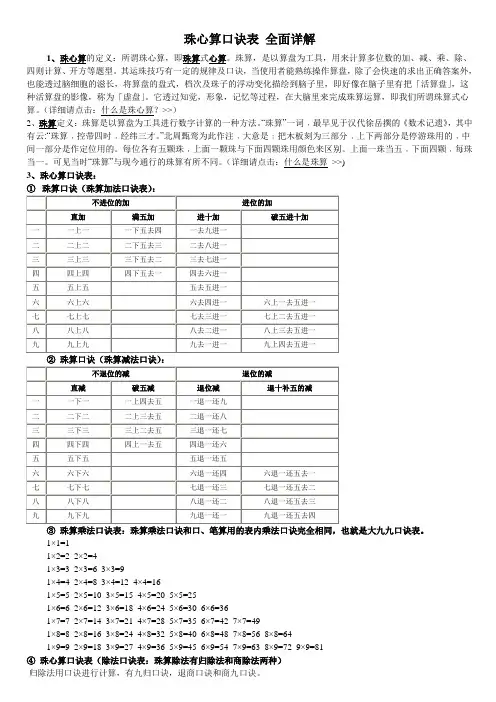
（详细请点击：什么是珠算 >>)3、珠心算口诀表： ① 珠算口诀（珠算加法口诀表） ： 不进位的加 进位的加 直加 满五加 一 一上一 一下五去四 二 二上二 二下五去三 三 三上三 三下五去二 四 四上四 四下五去一 五 五上五 六 六上六七 七上七 八 八上八 九 九上九 进十加 破五进十加 一去九进一 二去八进一 三去七进一 四去六进一 五去五进一 六去四进一 六上一去五进一 七去三进一 七上二去五进一 八去二进一 八上三去五进一 九去一进一 九上四去五进一② 珠算口诀（珠算减法口诀） ：不退位的减 退位的减直减 破五减 退位减 退十补五的减 一一下一 一上四去五 一退一还九 二二下二 二上三去五 二退一还八 三三下三 三上二去五 三退一还七 四四下四 四上一去五 四退一还六 五五下五 五退一还五 六六下六 六退一还四 六退一还五去一 七七下七 七退一还三 七退一还五去二 八八下八 八退一还二 八退一还五去三 九 九下九九退一还一 九退一还五去四③ 珠算乘法口诀表：珠算乘法口诀和口、笔算用的表内乘法口诀完全相同，也就是大九九口诀表。

1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81④珠心算口诀表（除法口诀表：珠算除法有归除法和商除法两种）归除法用口诀进行计算，有九归口诀，退商口诀和商九口诀。

九归口诀共61句：一归(用1除)：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九。

二归(用2除)：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五。

三归(用3除)：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二。

四归(用4除)：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二。

五归(用5除)：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八。

六归(用6除)：逢六进一，逢十二进二，六三添作五，六一下加四，六二三余二，六四六余四，六五八余二。

七归(用7除)：逢七进一，逢十四进二，七一下加三，七二下加六，七三四余二，七四五余五，七五七余一，七六八余四。

八归(用8除)：逢八进一，八四添作五，八一下加二，八二下加四，八三下加六，八五六余二，八六七余四，八七八余六。

九归(用9除)：逢九进一，九一下加一，九二下加二，九三下加三，九四下加四，九五下加五，九六下加六，九七下加七，九八下加八。

退商口诀共9句：无除退一下还一，无除退一下还二，无除退一下还三无除退一下还四，无除退一下还五，无除退一下还六无除退一下还七，无除退一下还八，无除退一下还九商九口诀共9句：见一无除作九一，见二无除作九二，见三无除作九三见四无除作九四，见五无除作九五，见六无除作九六见七无除作九七，见八无除作九八，见九无除作九九除数是一位数的除法叫“单归”;除数是两位或两位以上的除法叫“归除”，除数的首位叫“归”，以下各位叫“除”。

如，除数是534的归除，叫“五归三四除”，即用五归口诀求商后，再用34除。

1×3=3 2×3=6 3×3=91×4=4 2×4=8 3×4=12 4×4=161×5=5 2×5=10 3×5=15 4×5=20 5×5=251×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=361×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=491×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=641×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81④珠心算口诀表（除法口诀表：珠算除法有归除法和商除法两种）归除法用口诀进行计算，有九归口诀，退商口诀和商九口诀。

九归口诀共61句：一归(用1除)：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九。

二归(用2除)：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五。

三归(用3除)：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二。

四归(用4除)：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二。

五归(用5除)：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八。

六归(用6除)：逢六进一，逢十二进二，六三添作五，六一下加四，六二三余二，六四六余四，六五八余二。

七归(用7除)：逢七进一，逢十四进二，七一下加三，七二下加六，七三四余二，七四五余五，七五七余一，七六八余四。

创作编号：GB8878185555334563BT9125XW创作者：凤呜大王*创作编号：GB8878185555334563BT9125XW创作者：凤呜大王*1×3=3 2×3=6 3×3=91×4=4 2×4=8 3×4=12 4×4=161×5=5 2×5=10 3×5=15 4×5=20 5×5=251×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=361×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=491×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=641×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81④珠心算口诀表（除法口诀表：珠算除法有归除法和商除法两种）归除法用口诀进行计算，有九归口诀，退商口诀和商九口诀。

九归口诀共61句：一归(用1除)：逢一进一，逢二进二，逢三进三，逢四进四，逢五进五，逢六进六，逢七进七，逢八进八，逢九进九。

二归(用2除)：逢二进一，逢四进二，逢六进三，逢八进四，二一添作五。

三归(用3除)：逢三进一，逢六进二，逢九进三，三一三余一，三二六余二。

四归(用4除)：逢四进一，逢八进二，四二添作五，四一二余二，四三七余二。

五归(用5除)：逢五进一，五一倍作二，五二倍作四，五三倍作六，五四倍作八。

大班数学教案：两位数的直加直减一、教学目标1.让学生理解什么是两位数的直加直减运算。

2.能够使用竖式计算两位数的直加直减运算。

3.培养学生的计算能力和思维能力。

二、教学重难点1.教学重点：让学生掌握两位数的直加直减运算，并能够进行竖式计算。

2.教学难点：对于一些理解较慢的学生，需要加强教师的辅导和讲解。

三、教学内容及过程1. 导入（5分钟）1.用口算减法练习题开始导入，例如：52 - 18 = ？ 36 - 21 = ？。

2.询问学生如果直接口算两位数的减法计算困难时我们要如何计算呢？如有将不同的数位竖式排列，走顺序进行计算。

2. 观察讨论（15分钟）1.构建“鱼塘”模型，将模型展示给学生。

2.让学生一起观察讨论模型，由学生主导发言，引导学生发现模型中的规律。

通过引导孩子自主思考，让他们建立自信和兴趣。

3.师生互动，教师提问题，学生回答，发表个人观点进行检验和修改。

3. 教学过程（25分钟）1.初始练习设计思路：以打牌的方式进行。

（牌桌、牌子、纸牌）。

操作方式：让学生把牌桌、牌子、纸牌组成两位数，找到两位数后将纸牌加到位上，然后降序排列进行减法运算。

初步引导学生使用组合牌、分解牌、降序排列的思路进行近似计算。

记录大家有哪些方法来计算两位数的减法运算。

2.教授竖式计算两位数的加减法设计思路：举例、讲解、实例计算。

操作方式：让学生看讲解PPT，同时，将PPT上的竖式展示在黑板上，逐行讲解每个位数的计算方式。

4. 发散拓展（10分钟）1.让学生利用桌面上任意两个数进行加减法计算，并用竖式进行计算验证。

2.让学生将学过的计算方法用于社会生活中去，如何把它应用到日常生活中？四、教学评价1.通过阶段性的测试，检查学生的学习效果。

2.综合考虑学生口述、书面、实际应用等多方面的表现进行综合成绩评定。

五、教学反思1.软件和材料的准备比较充分。

2.教学中引导学生思考提问，得出学生的答案并实现教学目标的算法来计算快速达到效果。

1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=641×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81④珠心算口诀表（除法口诀表：珠算除法有归除法和商除法两种）归除法用口诀进行计算，有九归口诀,退商口诀和商九口诀。

九归口诀共61句：一归（用1除)：逢一进一，逢二进二，逢三进三，逢四进四,逢五进五，逢六进六，逢七进七，逢八进八，逢九进九.二归(用2除):逢二进一，逢四进二，逢六进三,逢八进四，二一添作五.三归（用3除）:逢三进一，逢六进二,逢九进三,三一三余一，三二六余二。

四归(用4除）：逢四进一，逢八进二，四二添作五,四一二余二，四三七余二.五归（用5除):逢五进一，五一倍作二，五二倍作四，五三倍作六,五四倍作八。

六归（用6除）：逢六进一，逢十二进二，六三添作五,六一下加四,六二三余二，六四六余四，六五八余二。

七归（用7除)：逢七进一,逢十四进二,七一下加三,七二下加六，七三四余二,七四五余五，七五七余一,七六八余四.八归(用8除):逢八进一，八四添作五，八一下加二,八二下加四，八三下加六，八五六余二，八六七余四，八七八余六。

九归(用9除）：逢九进一,九一下加一，九二下加二，九三下加三，九四下加四，九五下加五,九六下加六,九七下加七，九八下加八.退商口诀共9句：无除退一下还一，无除退一下还二，无除退一下还三无除退一下还四，无除退一下还五，无除退一下还六无除退一下还七，无除退一下还八，无除退一下还九商九口诀共9句：见一无除作九一，见二无除作九二，见三无除作九三见四无除作九四，见五无除作九五,见六无除作九六见七无除作九七,见八无除作九八，见九无除作九九除数是一位数的除法叫“单归"；除数是两位或两位以上的除法叫“归除”，除数的首位叫“归"，以下各位叫“除".如,除数是534的归除，叫“五归三四除"，即用五归口诀求商后，再用34除。

两位数直加直减题库
两位数的直加直减题库涵盖了各种不同类型的题目，包括进位不进位的加法和借位不借位的减法。

举例来说，对于直加题目，我们可以考虑以下类型的题目：
1. 无进位加法，例如 23 + 14。

2. 有进位加法，例如 47 + 38。

3. 跨十加法，例如 56 + 48。

4. 连加，例如 25 + 14 + 36。

对于直减题目，我们可以考虑以下类型的题目：
1. 无借位减法，例如 53 27。

2. 有借位减法，例如 68 39。

3. 跨十减法，例如 75 48。

4. 连减，例如 82 15 27。

除了基本的加法和减法题目外，还可以设计一些应用题，让学生在解决问题的同时培养逻辑思维能力。

此外，可以考虑加入一些有趣的数字游戏，让学生通过游戏的方式进行练习，增加趣味性和互动性。

在设计题目时，需要注意题目的难度适当，考虑到学生的年龄和能力水平，逐步增加题目的复杂度，让学生在不断挑战中提高自己的计算能力。

同时，也要注意题目的多样性，让学生接触到不同类型的题目，培养他们的综合运算能力。

总的来说，两位数的直加直减题库应该涵盖多种类型的题目，既要注重基础的计算能力训练，又要注重培养学生的逻辑思维能力和解决问题的能力。

希望这些内容能够帮助你更好地设计和组织两位数直加直减题库。