基本初等函数(3)

初等基本函数知识点总结函数是数学中最基本的概念之一，它在数学的各个分支中都有着重要的应用。

初等基本函数是指在初等数学范围内常见的基本函数，包括常数函数、一次函数、二次函数、指数函数、对数函数、幂函数、三角函数等。

本文将对这些初等基本函数的概念、性质等进行总结和介绍。

一、常数函数常数函数的定义是f(x) = c （c为常数）。

这里的c就是常数函数的函数值，它是一个常数，和x的取值无关。

在坐标系中，常数函数的图象是一条水平的直线，它的斜率为0。

常数函数的性质有：1. 常数函数的图象是一条水平的直线。

2. 常数函数的定义域是全体实数集R，值域为{c}。

3. 常数函数的导数为0，即f'(x) = 0。

4. 常数函数是一个一一对应的函数。

5. 常数函数是奇函数，偶函数，周期函数，增函数，减函数等的特殊情况。

二、一次函数一次函数的定义是f(x) = kx + b （k和b为常数，k≠0）。

在坐标系中，一次函数的图象是一条通过点P(k，b)的直线，它的斜率为k，截距为b。

一次函数的性质有：1. 一次函数的图象是一条直线，斜率k决定了直线的倾斜程度，截距b决定了直线与y轴的交点位置。

2. 一次函数的定义域是全体实数集R，值域是一切实数集R。

3. 一次函数的导数为k，即f'(x) = k。

4. 当k>0时，一次函数是增函数；当k<0时，一次函数是减函数；当k=0时，一次函数是常数函数。

5. 一次函数是一个奇函数，因为f(-x) = -kx + b = -f(x)。

三、二次函数二次函数的定义是f(x) = ax^2 + bx + c （a、b和c为常数，a≠0）。

二次函数的图象是一个开口向上或者向下的抛物线，它的开口方向由a的正负决定。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

二次函数的性质有：1. 二次函数的图象是一个抛物线，它关于y轴对称，对称轴方程为x = -b/2a。

基本初等函数包括以下几种：（1）常数函数y = c（c 为常数）（2）幂函数y = x^a（a 为非0 常数）（3）指数函数y = a^x（a＞0, a≠1）（4）对数函数y =log(a) x（a＞0, a≠1）（5）三角函数：主要有以下6 个：正弦函数y =sin x余弦函数y =cos x正切函数y =tan x余切函数y =cot x正割函数y =sec x余割函数y =csc x此外，还有正矢、余矢等罕用的三角函数。

（6）反三角函数：主要有以下6 个：反正弦函数y = arcsin x反余弦函数y = arccos x反正切函数y = arctan x反余切函数y = arccot x反正割函数y = arcsec x反余割函数y = arccsc x初等函数是由基本初等函数经过有限次的有理运算和复合而成的函数。

基本初等函数和初等函数在其定义区间内均为连续函数幂函数简介形如y=x^a(a为常数）的函数，即以底数为自变量幂为因变量，指数为常量的函数称为幂函数。

当a取非零的有理数时是比较容易理解的，而对于a取无理数时，初学者则不大容易理解了。

因此，在初等函数里，我们不要求掌握指数为无理数的问题，只需接受它作为一个已知事实即可，因为这涉及到实数连续统的极为深刻的知识。

特性对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：首先我们知道如果a=p/q，且p/q为既约分数（即p、q互质），q和p都是整数，则x^(p/q)=q 次根号下（x的p次方），如果q是奇数，函数的定义域是R，如果q是偶数，函数的定义域是[0,＋∞）。

当指数a是负整数时，设a=-k，则y=1/(x^k)，显然x≠0，函数的定义域是（－∞，0)∪(0,＋∞)。

因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：排除了为0与负数两种可能，即对于x>0，则a可以是任意实数；排除了为0这种可能，即对于x<0或x>0的所有实数，q不能是偶数；排除了为负数这种可能，即对于x为大于或等于0的所有实数，a就不能是负数。

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数（y=C）（1）定义域: D（f）＝（-∞，+∞）（2）值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0，C)在y轴上截距为C的直线(4 )图像：(5)周期性：常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T，f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义：形如y=x^a(a为常数）的函数，即以底数为自变量，幂为因变量，指数为常量的函数称为幂函数.(2)性质：在(0，+∞)内总有意义①当α＞0时函数图像过点(0，0)和(1，1)，在(0，+∞)内单调增加且无界②当α＜0时函数图像过点(1，1)，在(0，+∞)内单调减少且无界(3)图像：3.指数函数y=a^x(a>0且a≠1)(1)定义域：x∈R(2)值域：(0，+∞)(3)性质：①单调性：1.当0＜a＜1时，在(-∞，+∞)内单调减少 2.当a ＞1时，在(-∞，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(4)图像：①由指数函数y=a^x与直线x=1相交于点（1，a)可知：在y轴右侧，图像从下到上相应的底数由小变大。

②由指数函数y=a^x与直线x=-1相交于点（-1，1/a）可知：在y轴左侧，图像从下到上相应的底数由大变小。

③指数函数的底数与图像间的关系可概括的记忆为：在y轴右边“底大图高”；在y轴左边“底大图低” 如图：(5)运算法则：①②③④4.对数函数y=logax（a>0 且a≠1）(1)定义：如果a^x=N（a>0，且a ≠1），那么数x叫做以a为底N的对数，记作x=logaN，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数一般地，函数y=logax（a>0，且a ≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数(2)定义域：(0，+∞)，即x>0(3)值域：R(4)性质：①单调性：1.当0＜a＜1时，在(0，+∞)内单调减少 2.当a ＞1时，在(0，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(5)图像：【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式：5.三角函数⑴正弦函数y=sin x(1)定义：对边与斜边的比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ(K∈Z)时，Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：奇函数③对称性：对称中心是(Kπ,0)，K ∈Z；对称轴是直线x=Kπ+π/2，K ∈Z④单调性：在[2Kπ-π/2,2Kπ+π/2]，K∈Z上单调递增；在[2Kπ+π/2,2Kπ+3π/2]，K∈Z上单调递减⑤有界性：有界函数(6)图像：(2)余弦函数y=cos x(1)定义：邻边与斜边之比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ +π /2(K∈Z)时，Y取最大值1 2.当X=2Kπ +π (K∈Z)时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：偶函数③对称性：对称中心是(Kπ+π/2,0)，K∈Z；对称轴是直线x=Kπ，K∈Z④单调性：在[2Kπ,2Kπ+π]，K∈Z上单调递减；在[2Kπ+π,2Kπ+2π]，K∈Z上单调递增⑤有界性：有界函数(6)图像：(3)正切函数y=tan x(1)定义：对边与邻边之比(2)定义域：{x∣x≠Kπ+π/2,K∈Z}(3)值域：R(4)最值：无最大值和最小值(5)性质：①周期性：最小正周期都是πT=π②奇偶性：奇函数③对称性：对称中心是(Kπ/2,0)，K∈Z④单调性：在[Kπ-π/2,Kπ+π/2]，K∈Z上单调递增⑤有界性：无界函数(6)图像：(4)余切函数y=cot x(1)定义：在直角三角形中，某锐角的相邻直角边和相对直角边的比，叫做该锐角的余切。

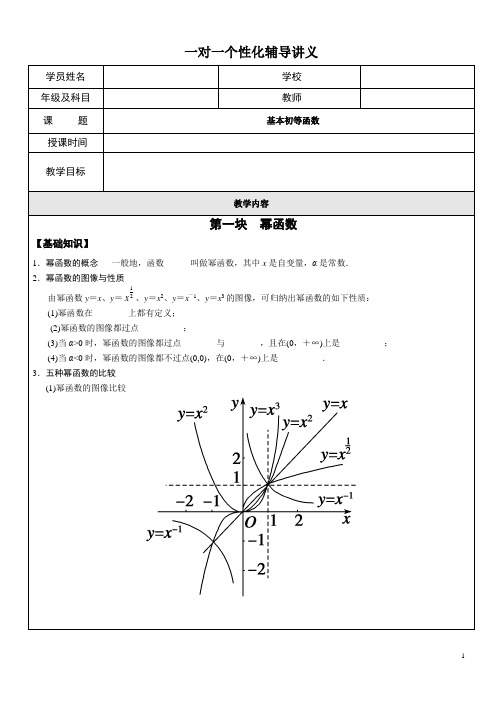
一对一个性化辅导讲义学员姓名学校年级及科目教师课题基本初等函数授课时间教学目标教学内容第一块幂函数【基础知识】1．幂函数的概念一般地，函数______叫做幂函数，其中x是自变量，α是常数．2．幂函数的图像与性质由幂函数y＝x、y＝12x、y＝x2、y＝x－1、y＝x3的图像，可归纳出幂函数的如下性质：(1)幂函数在________上都有定义；(2)幂函数的图像都过点__________；(3)当α>0时，幂函数的图像都过点________与________，且在(0，＋∞)上是__________；(4)当α<0时，幂函数的图像都不过点(0,0)，在(0，＋∞)上是__________．3．五种幂函数的比较(1)幂函数的图像比较(2)幂函数的性质比较函数 特征 性质y ＝x y ＝x 2y ＝x 3y ＝12x y ＝x －1定义域 值域 奇偶性 单调性[疑难点]1．在(0,1)上，幂函数中指数越大，函数图像越靠近x 轴(简记为“指大图低”)，在(1，＋∞)上幂函数中指数越大，函数图像越远离x 轴．2．幂函数的图像一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图像最多只能同时出现在两个象限内；如果幂函数图像与坐标轴相交，则交点一定是原点．[题型分类解析][题型一] 幂函数的定义及应用例1 已知y ＝(m 2＋2m －2)·211m x -＋(2n －3)是幂函数，求m 、n 的值．[训练1]已知f (x )＝(m 2＋2m )21m m x＋－，m 为何值时，f (x )是：(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数．[题型二] 幂函数的图像及性质的简单应用例2 已知幂函数f (x )的图像过点(2，2)，幂函数g (x )的图像过点12,4⎛⎫ ⎪⎝⎭. (1)求f (x )，g (x )的解析式；(2)当x 为何值时，①f (x )>g (x )；②f (x )＝g (x )；③f (x )<g (x )． [训练2] 已知幂函数y ＝243m m x －－(m ∈Z )的图像与y 轴有公共点，且其图像关于y 轴对称，求m 的值，并作出其图像．[题型三] 利用幂函数的性质比较幂值的大小 例3 比较下列各组数的大小：(1)13(0.95)和13(0.96)； (2)1-3-8和1319⎛⎫- ⎪⎝⎭； (3)0.20.5和0.40.3. [训练3]比较下列各组数的大小： (1)30.830.7； (2)0.2130.233； (3)122 131.8； (4)254.1 2-33.8 35(1.9).[题型四] 幂函数的综合应用 例4 已知幂函数f (x )＝223m m x －－(m ∈N *)的图像关于y 轴对称，且在(0，＋∞)上是减函数，求满足()31ma -+<3(32)m a -的a 的取值范围． [训练4](1)已知幂函数f (x )＝21()m m x－＋(m ∈N *)．(1)试确定该函数的定义域，并指明该函数在其定义域上的单调性；(2)若该函数还经过点(2，2)，试确定m 的值，并求满足条件f (2－a )>f (a －1)的实数a 的取值范围．(2)若函数f (x )＝3-24(+42)mx x m ++＋(x 2－mx ＋1)0的定义域为R ，求实数m 的取值范围．[课堂总结]1．幂函数y ＝x α(α∈R )，其中α为常数，其本质特征是以幂的底x 为自变量，指数α为常数，这是判断一个函数是否是幂函数的重要依据和唯一标准．应当注意并不是任意的一次函数、二次函数都是幂函数，如y ＝x ＋1，y ＝x 2－2x 等都不是幂函数．2．比较多个幂值的大小，一般采用媒介法，即先判断这组数中每个幂值与0,1等数的大小关系，据此将它们分成若干组，然后将同一组内的各数再利用相关方法进行比较，最终确定各数之间的大小关系．3．幂函数y ＝x α的图像与性质由于α的值不同而比较复杂，一般从两个方面考查：(1)α>0时，图像过(0,0)，(1,1)在第一象限的图像上升；α<0时，图像不过原点，在第一象限的图像下降，反之也成立． (2)曲线在第一象限的凹凸性α>1时，曲线下凸；0<α<1时，曲线上凸；α<0，曲线下凸．[课堂检测]（4分钟）1．当α∈11,,1,32⎧⎫-⎨⎬⎩⎭时，幂函数y ＝x α的图像不可能经过第________象限． 2．已知幂函数f (x )＝k ·x α的图像过点12,22⎛⎫⎪ ⎪⎝⎭，则k ＋α＝________. 3．下列函数是幂函数的序号是________．①y ＝2x ②y ＝2x －1 ③y ＝(x ＋2)2 ④y ＝3x 2 ⑤y ＝1x4．已知幂函数f (x )＝x α的图像经过点22,2⎛⎫⎪ ⎪⎝⎭，则f (4)的值等于( )A ．16B.116C ．2D.125.（2010安徽）设52535252,52,53⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛=c b a ，则,,,c b a 大小关系是_______________.第二块 指数与指数函数【基础知识】 1．根式(1)根式的概念如果一个数的n 次方等于a (n ＞1且n ∈N *)，那么这个数叫做a 的n 次方根．也就是，若x n ＝a ，则x 叫做__________，其中n ＞1且n ∈N *.式子 na 叫做__________，这里n 叫做__________，a 叫做____________．(2)根式的性质①当n 为奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数，这时，a 的n 次方根用符号________表示．②当n 为偶数时，正数的n 次方根有两个，它们互为相反数，这时，正数a 的正的n 次方根用符号________表示，负的n 次方根用符号________表示．正负两个n 次方根可以合写为________(a ＞0)． ③( na )n ＝______.④当n 为奇数时， na n ＝______； 当n 为偶数时，na n ＝|a |＝______________. ⑤负数没有偶次方根． 2．有理数指数幂(1)幂的有关概念①正整数指数幂：a n ＝n a a a ∙∙∙个(n ∈N *)． ②零指数幂：a 0＝______(a ≠0)．③负整数指数幂：a －p ＝________(a ≠0，p ∈N *)．④正分数指数幂：mna＝______(a>0，m、n∈N*，且n>1)．⑤负分数指数幂：-mna＝__________＝________ (a>0，m、n∈N*，且n>1)．⑥0的正分数指数幂等于______，0的负分数指数幂____________．(2)有理数指数幂的性质①a r a s＝__________(a>0，r、s∈Q)；②(a r)s＝________(a>0，r、s∈Q)；③(ab)r＝__________(a>0，b>0，r∈Q)．3．指数函数的图像与性质y＝a x a>10<a<1图像定义域(1)____值域(2)________性质(3)过定点________(4)当x>0时，______；x<0时，________(5)当x>0时，________；x<0时，_______(6)在(－∞，＋∞)上是______(7)在(－∞，＋∞)上是_____题型一指数式与根式的计算问题例1 已知11223x x-+=则=-+-+--84221xxxx。

三种基本初等函数（一）指数与指数幂的运算1．根式的概念一般地，如果a x n=，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *．当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数．此时，a 的n 次方根用符号n a 表示．式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．由此可得：负数没有偶次方根；0的任何次方根都是0，记作00=n ． 2．分数指数幂正数的分数指数幂的意义规定：)1,,,0(*>∈>=n N n m a a a n m nm )1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义指出：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂．3．无理指数幂指出：一般地，无理数指数幂),0(是无理数αα>a a 是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．4.有理指数幂的运算性质（1）r a ·sr r aa += ),,0(Q s r a ∈>； （2）rssr a a =)( ),,0(Q s r a ∈>； （3）srra a ab =)(),0,0(Q r b a ∈>>．（二）指数函数的概念一般地，函数)1a ,0a (a y x≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：○1 指数函数的定义是一个形式定义；指数函数的图象和性质定义域值域单调性过定点 随堂练习 一．选择题：1．函数y=－e x 的图象（ ） A.与y =e x 的图象关于y 轴对称 B.与y =e x 的图象关于坐标原点对称C.与y =e －x 的图象关于y 轴对称D.与y =e －x 的图象关于坐标原点对称 2．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）。

基本初等函数证明首先，我们来讨论基本初等函数的定义。

基本初等函数是指由常数函数、指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次的四则运算和函数复合得到的函数。

对于这些函数，我们可以通过一些基本的性质和定理来进行证明。

一、常数函数：常数函数是指对于任意实数x，函数值都是一个常数。

常数函数的性质很简单，我们可以通过以下例子来进行证明：例1：证明常数函数的导数为0。

已知常数函数为f(x) = a，其中a为常数。

对于任意实数x1和x2，它们的差为Δx = x2 - x1，则有f(x2) - f(x1) = a - a = 0。

由导数的定义可知，导数f'(x) = lim（Δx->0）（f(x2) - f(x1)）/（x2 - x1） = 0。

二、指数函数：指数函数是以常数e（自然对数的底）为底的幂函数。

它具有以下性质：性质1：指数函数f(x) = e^x的导数为它本身。

证明：根据指数函数的定义，知道f(x+h) = e^(x+h) = e^x * e^h，所以f'(x) = lim（h->0）（f(x+h) - f(x)）/h = lim（h->0）(e^x *e^h - e^x) / h = e^x * lim（h->0）(e^h - 1) / h。

由于lim（h->0）(e^h - 1) / h = 1，所以f'(x) = e^x。

性质2：指数函数的导数等于它的斜率。

证明：由指数函数的导数f'(x) = e^x可得，函数f(x)在任意一点的斜率等于e^x，也就是说切线的斜率等于函数值。

三、对数函数：对数函数是指以指数为底的幂函数的反函数。

以下是对数函数的性质：性质1：对数函数f(x) = log_a(x)（a>0且a≠1）的导数为1 /（x * ln(a)）。

证明：由对数函数的定义可知，对于任意实数x1和x2，x1 =a^y1，x2 = a^y2。